10.7 以原产物为中心绘制超高光谱图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 以来源地为中心绘制超光谱图

  Collapse Expand

  以来源地为中心绘制超光谱图

  播放段落

  Your homework assignment is to graph the $\begin{align*}9y^2 - 4x^2 = 36\end{align*}$ . What are the asymptotes and foci of your graph?
  ::您的作业任务是绘制 9y2 - 4x2=36 。 您的图表中什么是小数和小数 ?

  播放段落

  Graphing Hyperbolas
  ::超分层图

  播放段落

  We know that the resulting graph of a rational function is a hyperbola with two branches . A hyperbola is also a conic section. To create a hyperbola, you would slice a plane through two inverted cones, such that the plane is perpendicular to the bases of the cones.
  ::我们知道,理性函数的图解是具有两个分支的超大波拉。超大波拉也是一个二次曲线部分。要创建超大波拉,你可以通过两个反向的锥形切开一个平面,使该平面与锥形的底部垂直。

  

  播放段落

  By the conic definition, a hyperbola is the set of all points such that the of the differences of the distances from the foci is constant.
  ::根据二次曲线的定义,超重波是所有点的组合,因此与福子距离的差异是恒定的。

  

  播放段落

  Using the picture, any point, $\begin{align*}(x, y)\end{align*}$ on a hyperbola has the property, $\begin{align*}d_1-d_2=P\end{align*}$ , where $\begin{align*}P\end{align*}$ is a constant.
  ::使用图片时,超高波拉上的任何点(x,y)都具有该属性,即P为常数的 d1-d2=P。

  播放段落

  Comparing this to the ellipse, where $\begin{align*}d_1+d_2=P\end{align*}$ and the equation was $\begin{align*}\frac{x^2}{a^2} + \frac{y^2}{b^2}=1\end{align*}$ or $\begin{align*}\frac{x^2}{b^2} + \frac{y^2}{a^2}=1\end{align*}$ .
  ::将此比作椭圆, d1+d2=P 和方程式为 x2a2+y2b2=1 或 x2b2+y2a2=1 。

  播放段落

  For a hyperbola, then, the equation will be $\begin{align*}\frac{x^2}{a^2} - \frac{y^2}{b^2}=1\end{align*}$ or $\begin{align*}\frac{y^2}{a^2} - \frac{x^2}{b^2}=1\end{align*}$ . Notice in the vertical orientation of a hyperbola, the $\begin{align*}y^2\end{align*}$ term is first. Just like with an ellipse, there are two vertices , on the hyperbola. Here, they are the two points that are closest to each other on the graph. The line through the vertices and foci is called the transverse axis . Its midpoint is the center of the hyperbola. In this concept, the center will be the origin. There will always be two branches for any hyperbola and two asymptotes.
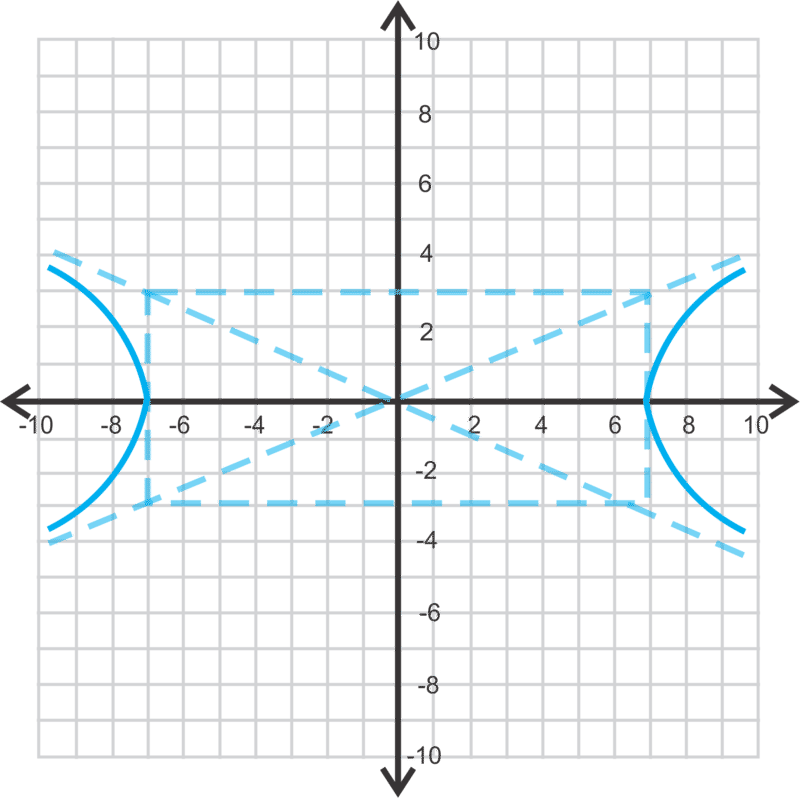
  ::对于双曲线, 方程式将是 x2a2- y2b2=1 或 y2a2- x2b2=1 。 在双曲线的垂直方向中注意, y2 术语为第一。 就像 椭圆 一样, 在 双曲线上有两个顶点。 这里, 它们是图形上两个最接近的点 。 横脊和 foci 之间的线被称为横轴 。 其中点是高曲线的中心 。 在这个概念中, 中心将是源头 。 任何超曲线总是有两个分支 , 并且有两个小孔 。

  

  

  播放段落

  Let's graph $\begin{align*}\frac{x^2}{64} - \frac{y^2}{25}=1\end{align*}$  and then find the vertices, foci, and asymptotes.
  ::让我们绘制图 x264 -y225=1, 然后找到顶部、 foci 和 asymptotes 。

  播放段落

  First, this hyperbola has a horizontal transverse axis because the $\begin{align*}x^2\end{align*}$ term is first. Also, with hyperbolas, the $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ term stay in place, but the $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ terms switch. $\begin{align*}a\end{align*}$ is not always greater than $\begin{align*}b\end{align*}$ .
  ::首先,这个超双曲线有一个横向反向轴, 因为 x2 术语是第一个 。 另外, 如果有超光子, a 和 b 术语将保持原位, 但 x 和 y 术语开关不总是大于 b 。 ais

  播放段落

  Therefore, $\begin{align*}a=\sqrt{64}=8\end{align*}$ and $\begin{align*}b=\sqrt{25}=5\end{align*}$ . To graph this hyperbola, go out 8 units to the left and right of the center and 5 units up and down to make a rectangle. The diagonals of this rectangle are the asymptotes.
  ::因此, a64=8 和 b25=5 。 要绘制此双曲线图, 请从中间的左边和右边出8个单位, 向上和向下出5个单位, 以形成矩形。 此矩形的对角是小行星 。

  播放段落

  Draw the hyperbola branches with the vertices on the transverse axis and the rectangle. Sketch the branches to get close to the asymptotes, but not touch them.
  ::绘制横轴和矩形上的双波形树枝。 将树枝拉伸以接近小行星, 但不触动它们 。

  

  播放段落

  The vertices are $\begin{align*}(\pm 8, 0)\end{align*}$ and the asymptotes are $\begin{align*}y=\pm \frac{5}{8}x\end{align*}$ (see pictures above. To find the foci, we use the Pythagorean Theorem, $\begin{align*}c^2=a^2+b^2\end{align*}$ because the foci are further away from the center than the vertices.
  ::脊椎是 (8,0) , 微粒是 y58x( 见上文图片 。 要找到 foci, 我们使用 Pythagorean 理论, c2=a2+b2 , 因为 foci 离中心远比 verps 远 。

  播放段落

  $$\begin{align*}c^2 &= 64+25=89 \\ c &= \sqrt{89}\end{align*}$$
  ::c2=64+25=89c89

  播放段落

  The foci are $\begin{align*}\left(\pm \sqrt{89}, 0 \right)\end{align*}$ .
  ::焦点是(89,0)。

  播放段落

  Now, let's graph $\begin{align*}36y^2 - 9x^2=324\end{align*}$  and identify the foci.
  ::现在,让我们绘制36y2-9x2=324的图表, 并辨别方位。

  播放段落

  This equation is not in standard form. To rewrite it in standard form, the right side of the equation must be 1. Divide everything by 324.
  ::此方程式不是标准格式。 要重写标准格式, 方程式的右侧必须是 1. 将所有方程式除以324 。

  播放段落

  $$\begin{align*}\frac{36y^2}{324} - \frac{9x^2}{324} &= \frac{324}{324} \\ \frac{y^2}{9} - \frac{x^2}{36} &=1\end{align*}$$
  ::36y2324-9x2324=324324y29-x236=1

  播放段落

  Now, we can see that this is a vertical hyperbola, where $\begin{align*}a=3\end{align*}$ and $\begin{align*}b=6\end{align*}$ . Draw the rectangle, asymptotes, and plot the vertices on the $\begin{align*}y\end{align*}$ -axis.
  ::现在,我们可以看到,这是一个垂直的双曲线, a=3和b=6。 绘制矩形, 星状图, 并在 Y 轴上绘制顶部 。

  

  播放段落

  To find the foci, use $\begin{align*}c^2=a^2+b^2\end{align*}$ .
  ::要找到 foci, 请使用 c2=a2+b2 。

  播放段落

  $$\begin{align*}c^2 &= 36+9=45 \\ c &= \sqrt{45} = 3\sqrt{5}\end{align*}$$
  ::c2=36+9=45c=45=35

  播放段落

  The foci are $\begin{align*}\left(0, 3 \sqrt{5}\right)\end{align*}$ and $\begin{align*}\left(0, -3 \sqrt{5}\right)\end{align*}$ .
  ::方块是(0,35)和(0,35)。

  播放段落

  Finally, let's graph $\begin{align*}\frac{x^2}{4} - \frac{y^2}{4}=1\end{align*}$  and identify the asymptotes.
  ::最后,让我们用图表 x24 -y24=1 来识别小行星。

  播放段落

  This will be a horizontal hyperbola, because the $\begin{align*}x\end{align*}$ -term is first. $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ will both be 2 because $\begin{align*}\sqrt{4}=2\end{align*}$ . Draw the square and diagonals to form the asymptotes.
  ::这将是一个水平双曲线, 因为 x 期是第一个。 a 和 b 将同时是 2 , 因为 '% 4= 2 。 绘制正方形和对角以形成小数 。

  

  播放段落

  The asymptotes are $\begin{align*}y= \pm \frac{2}{2}x\end{align*}$ or $\begin{align*}y=x\end{align*}$ and $\begin{align*}y=-x\end{align*}$ .
  ::22x 或 y=x 和 yx 是 y22x 或 y=x 和 yx 。

  播放段落

  Important Note: The asymptotes and square are not a part of the function. They are included in graphing a hyperbola because it makes it easier to do so.
  ::重要注意: 微粒和正方形不是函数的一部分。 它们被包含在超大波拉的图形中, 因为这样更容易做到 。

  播放段落

  Also, when graphing hyperbolas, we are sketching each branch. We did not make a table of values to find certain points and then connect. You can do this, but using the square or rectangle with the asymptotes produces a pretty accurate graph and is much simpler.
  ::此外,在绘制超光谱图时,我们正在绘制每个分支的图。我们没有绘制一个数值表来查找某些点,然后连接。你可以做到这一点,但使用方形或与小行星的矩形来绘制一个非常准确的图表,并且简单得多。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find  the asymptotes and foci of your graph. 
  ::早些时候,你被要求 找到您的图表的微粒和角。

  播放段落

  First, we need to get the equation in the form $\begin{align*}\frac{y^2}{a^2} - \frac{x^2}{b^2}=1\end{align*}$ , so divide by 36.
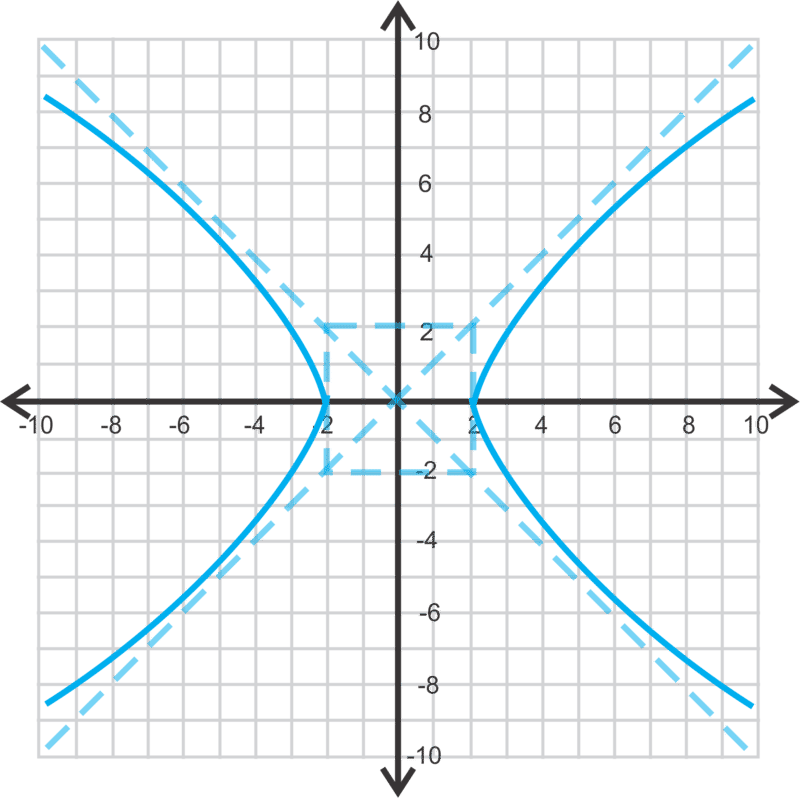
  ::首先,我们需要以 y2a2-x2b2=1 的形式获得方程式, 所以除以 36 。

  播放段落

  $$\begin{align*}9y^2 - 4x^2 = 36\\ \frac{9y^2}{36} - \frac{4x^2}{36} = \frac{36}{36}\\ \frac{y^2}{4} - \frac{x^2}{9} = 1\end{align*}$$
  ::9y2-4x2=369y236-4x236=3636y24-x29=1

  播放段落

  Now we can see that $\begin{align*}a^2 = 4\end{align*}$ and $\begin{align*}b^2 = 9\end{align*}$ , so $\begin{align*}a = 2\end{align*}$ and $\begin{align*}b = 3\end{align*}$ . Also, because the y -term comes first, the hyperbola is vertically oriented. Therefore, the asymptotes are $\begin{align*}y = -\frac{a}{b}x\end{align*}$ and $\begin{align*}y = \frac{a}{b}x\end{align*}$ .
  ::现在我们可以看到 a2=4 和 b2=9, 所以 a=2 和 b=3。 另外, 由于 Y 期先到, 双波拉是垂直方向的。 因此, 亚伯克斯和 y=abx 的微粒是 yabx 和 y=abx 。

  播放段落

  Substituting for a and b , we get $\begin{align*}y = -\frac{2}{3}x\end{align*}$ and $\begin{align*}y = \frac{2}{3}x\end{align*}$ .
  ::替换a和b, 我们得到y23x和y=23x。

  播放段落

  Finally, to find the foci, use $\begin{align*}c^2=a^2+b^2\end{align*}$ .
  ::最后,要找到角,请使用 c2=a2+b2。

  播放段落

  $$\begin{align*}c^2 &= 4+9=13 \\ c &= \sqrt{13}\end{align*}$$
  ::c2=4+9=13c=13

  播放段落

  The foci are $\begin{align*}\left(0, \sqrt{13}\right)\end{align*}$ and $\begin{align*}\left(0, -\sqrt{13}\right)\end{align*}$ .
  ::焦点是(0,/13)和(0,____)。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the vertices, foci, and asymptotes of $\begin{align*}y^2-\frac{x^2}{25}=1\end{align*}$ .
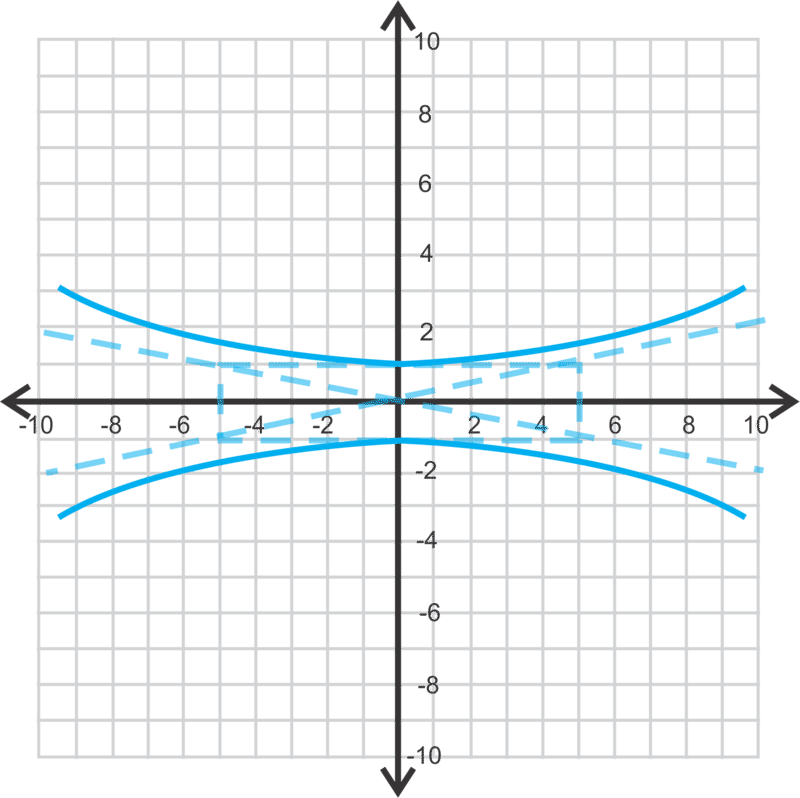
  ::查找 y2 - x225=1 的顶部、 福西 和 零位数 。

  播放段落

  First, let’s rewrite the equation like this: $\begin{align*}\frac{y^2}{1} - \frac{x^2}{25}=1\end{align*}$ . We know that the transverse axis is vertical because the $\begin{align*}y\end{align*}$ -term is first, making $\begin{align*}a=1\end{align*}$ and $\begin{align*}b=5\end{align*}$ . Therefore, the vertices are $\begin{align*}(0, -1)\end{align*}$ and $\begin{align*}(0, 1)\end{align*}$ . The asymptotes are $\begin{align*}y= \frac{1}{5}x\end{align*}$ and $\begin{align*}y= -\frac{1}{5}x\end{align*}$ . Lastly, let’s find the foci using $\begin{align*}c^2=a^2+b^2\end{align*}$ .
  ::首先,让我们重写这样的方程 : y21- x225=1. 我们知道, 横轴是垂直的, 因为 y- term 是第一个, 产生 a=1 和 b= 5。 因此, 顶端是 (0, 1) 和 (0, 1) 。 微粒是 y= 15x 和 y= 15x 。 最后, 我们使用 c2=a2+b2 来查找 foci 。

  播放段落

  $$\begin{align*}c^2 &= 1+25=26 \\ c &= \sqrt{26}\end{align*}$$
  ::c2=1+25=26c26

  播放段落

  The foci are $\begin{align*}\left(0, -\sqrt{26}\right)\end{align*}$ and $\begin{align*}\left(0, \sqrt{26}\right)\end{align*}$ .
  ::方块是(0,26)和(0,26)。

  播放段落

  Example 3
  ::例3

  播放段落

  Graph Example 2.
  ::图例2

  

  播放段落

  Example 4
  ::例4

  播放段落

  Graph $\begin{align*}9x^2-49y^2=411\end{align*}$ .
  ::图9x2-49y2=411。

  播放段落

  Rewrite the equation so that the right side is equal to 1. Divide everything by 441.
  ::重写方程式, 使右侧等于 1 。 将所有方程式除以 441 。

  播放段落

  $$\begin{align*}\frac{9x^2}{441} - \frac{49y^2}{441} &= \frac{441}{441} \\ \frac{x^2}{49} - \frac{y^2}{9} &= 1\end{align*}$$
  ::9x2441-49y2441=4414441x249-y29=1

  播放段落

  $\begin{align*}a=9\end{align*}$ and $\begin{align*}b=6\end{align*}$ with a horizontal transverse axis.
  ::a=9和b=6,具有横向横轴。

  

  播放段落

  Review
  ::回顾

  播放段落

  Find the vertices, asymptotes, and foci of each hyperbola below.
  ::找到下方每个超重波的脊椎, 微粒, 和角。

  播放段落
  1. $\begin{align*}\frac{x^2}{9} - \frac{y^2}{16} =1\end{align*}$
     ::x29-y216=1
  播放段落
  2. $\begin{align*}4y^2-25x^2=100\end{align*}$
     ::4y2-25x2=100
  播放段落
  3. $\begin{align*}\frac{x^2}{81} - \frac{y^2}{64} =1\end{align*}$
     ::x281-y264=1
  播放段落
  4. $\begin{align*}x^2-y^2=16\end{align*}$
     ::x2-y2=16
  播放段落
  5. $\begin{align*}\frac{y^2}{49} - \frac{x^2}{25} =1\end{align*}$
     ::y249 - x225=1
  播放段落
  6. $\begin{align*}121y^2-9x^2=1089\end{align*}$
     ::121y2-9x2=1089
  播放段落
  7. $\begin{align*}y^2-x^2=1\end{align*}$
     ::y2 - x2=1
  播放段落
  8. $\begin{align*}\frac{x^2}{64} - \frac{y^2}{4} =1\end{align*}$
     ::x264-y24=1
  播放段落
  9. $\begin{align*}\frac{y^2}{4} - \frac{x^2}{64} =1\end{align*}$
     ::y24 - x264=1
  播放段落
  10. Graph #1.
      ::图1。
  播放段落
  11. Graph #2.
      ::图2
  播放段落
  12. Graph #8.
      ::图8
  播放段落
  13. Graph #9.
      ::图9
  播放段落
  14. Writing Compare the hyperbolas from #8 and #9. How are they the same? How are they different? What do you know about the asymptotes and foci?
      ::比较8号和9号的超光球,它们如何相同?它们有什么不同?你对小行星和小行星了解多少?
  播放段落
  15. Critical Thinking Compare the equations $\begin{align*}\frac{x^2}{25} - \frac{y^2}{9} =1\end{align*}$ and $\begin{align*}\frac{x^2}{25} + \frac{y^2}{9} =1\end{align*}$ . Graph them on the same axes and find their foci.
      ::比较方程式 x225-y29=1 和 x225+y29=1. 在同一轴上标出它们并找到它们的角。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。