Course: 3.9 指数模型 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

指数模型

Suppose you were evaluating a particular site as a possible future location for your new car stereo store, "Rock can Roll". You know that in order to be successful, the store must be located in a town with a population of at least 100,000. You also know that you have saved up enough to carry you through the first two years of becoming established, so the town can start out a little under the minimum population as long as it will hit 100,000 by year three.
::假设你正在评估一个特定地点,作为你新的汽车立体录音店(Rock can Roll)未来的可能地点。你知道,为了成功,该商店必须位于一个人口至少为10万的城镇。你也知道,你存了足够的钱,可以将你带到成立后头两年,这样,只要到第三年达到10万,该镇就能从最低人口开始,从最低人口开始,只要到第三年达到10万。

The town you like best has a current population of 89,000, and is growing at a rate of 6% per year. Is it a big enough town for your store to be successful?
::最受欢迎的城市人口目前为89,000人,每年以6%的速度增长。这是否足够让你的商店成功?

Exponential Models
::指数模型

can be a bit surprising, as it can seem to be rather slow at first. At some point though, an exponential function will (sometimes rather suddenly) begin to increase very rapidly.
::指数函数(有时是突然的 ) 开始快速增长。

Population growth can often be modeled with an exponential function (assuming population grows as a percentage of the current population, i.e. 8% per year).
::人口增长往往可以以指数函数为模型(假设人口增长占目前人口的百分比,即每年8%)。

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about a possible location for the new car stereo store.
::之前有人问过你新的汽车音响店可能在哪里

You need to find a town that will have a minimum population of 100,000 by the third year from now. The town you are considering has a population of 89,000, with a yearly growth rate of 6%. Will it work?
::您需要找到一个在三年前至少有10万人口的城镇。您考虑的城镇人口为89,000人,年增长率为6%。它能工作吗 ?

Final population is equal to initial population multiplied by the growth rate once each year.
::最后人口等于初始人口乘以每年一次的增长率。

That indicates that final population is: $\begin{align*}{[(P_i \cdot growth) \cdot growth] \cdot growth}\end{align*}$ … etc. Where $\begin{align*}P_i\end{align*}$ is i nitial population.
::这表明,最后的人口是:[(Picrowth) 增长...等等。Pi是最初的人口。

Using r for growth r ate, and x for years passed, this simplifies to the exponential function:
::使用 r 表示增长率, X 表示年复一年的增长率, 这简化为指数函数 :

$\begin{align*}P(f) = P_i \cdot r^{x}\end{align*}$
::P(f) = Pirx

In our town, the population after x years would be: $\begin{align*}P(x) = 89,000 \cdot (1.06)^{x}\end{align*}$
::在我们的城镇,X年之后的人口为:P(x)=89,000-(1.06)x

The beginning of the 3rd year will occur after 2 years have passed, substituting 2 in for x gives: $\begin{align*}P(2) = 89,000 \cdot (1.06)^{2}\end{align*}$
::第三年的年初将在两年过去了之后开始,替换2英寸的x给:P(2)=89,9(1.06)2

$\begin{align*}\therefore P(2) = 100,000.4\end{align*}$
::P(2)=100 000.4

The projected population is 100,000 (and 4/10... someone is pregnant!) in the 3rd year, just big enough.
::预测第三年人口为10万(4/10...有人怀孕了!),

Example 2
::例2

The population of a small town was 2,000 in the year 1950. The population increased over time, as shown by the values in the table below.
::1950年,一个小城镇的人口为2,000人,人口逐年增加,如下表所示。

What is the number of people added to the population yearly? Why is this question more complex than it seems?
::人口每年增加多少人? 为什么这个问题比看起来复杂?

Year (1950 = 0)	Population
0	2000
5	2980
10	4450
20	9900
30	22,000
40	50,000

If you plot these data points, you will see that the growth pattern is non-linear:
::如果您绘制了这些数据点, 你会看到增长模式是非线性 :

The population does not continue to increase by the same number of people each year, it rather increases by a percentage of the population at the end of each year, an exponential function.
::人口不再继续每年以同样数量增加,而是每年年底以人口百分比增加,这是一个指数性功能。

Example 3
::例3

Use a graphing calculator to find a function of the form y = a(b ^x ) that fits the data in the table.
::使用图形计算器来查找表y = a(bx)的函数,该函数符合表格中的数据。

Year (1950 = 0)	Population
0	2000
5	2980
10	4450
20	9900
30	22,000
40	50,000

Using a TI-83/84 graphing calculator to find an exponential function that best fits a set of data.
::使用 TI-83/84 图形计算计算器来找到最符合一组数据的指数函数。

Entering the data
::输入数据

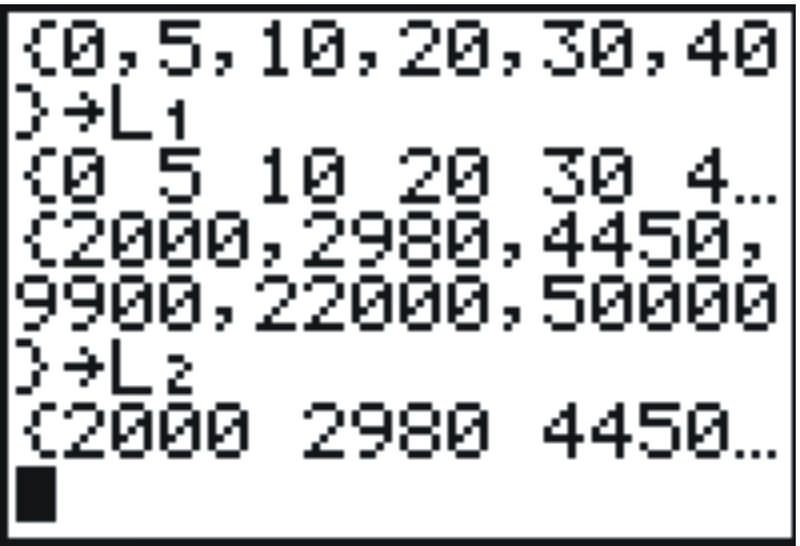
Data must be entered into “lists”. The calculator has six named lists, L1, L2, ... L6. We will enter the x values in L1 and the y values in L2. One way to do this is shown below:
::数据必须输入“列表”中。计算器有6个命名列表,L1、L2、......L6。我们将输入L1中的x值和L2中的y值。

Press [{] and then enter the numbers separated by commas, and close by pressing the following: [{] [L1].
::按 [{] 键,然后输入以逗号分隔的数字,然后按以下键关闭: [{] [L1]。

The top three lines of the figure below show the entry into list L1, followed by the entry of the y values into list L2.
::下图前三行显示列表L1中的条目,然后是列表L2中的Y值。

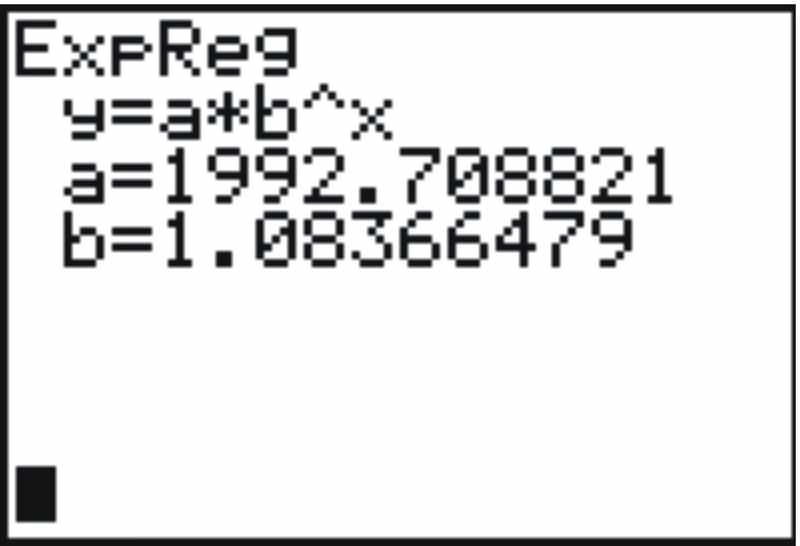
Now press , and move to the right to the CALC menu. Scroll down to option 10, ExpReg. Press , and you will return to the home screen. You should see ExpReg on the screen. As long as the numbers are in L1 and L2, the calculator will proceed to find an exponential function to fit the data you listed in List L1 and List L2. You should see on the home screen the values for a and b in the exponential function (See figure below).
::现在按下, 并移动到 CALC 菜单右侧。向下滚动到选项 10, Expreg. 按下, 您将返回到主屏幕上。您应该在屏幕上看到 Expreg 。只要数字在 L1 和 L2 中, 计算器将开始找到一个指数函数, 以匹配 L1 和 L2 列表中列出的数据。您应该在主屏幕上看到指数函数 a 和 b 的值( 见下表 )。

Therefore the function y = 1992.7(1.0837) ^x is an approximate model for the data.
::因此,函数y = 1992.7(1.0837x)是数据的大致模型。

Plotting the data and the equation
::绘制数据和方程

To view plots of the data points and the equation on the same screen, do the following.
::要在同一屏幕上查看数据点和方程式的图块,请做以下操作。

First, press and clear any equations.
::首先,按下并清除任何方程式。

You can type in the equation above, or to get the equation from the calculator, do the following:
::您可以在以上方程式中键入,或者从计算器中获取方程式,可以做以下操作:

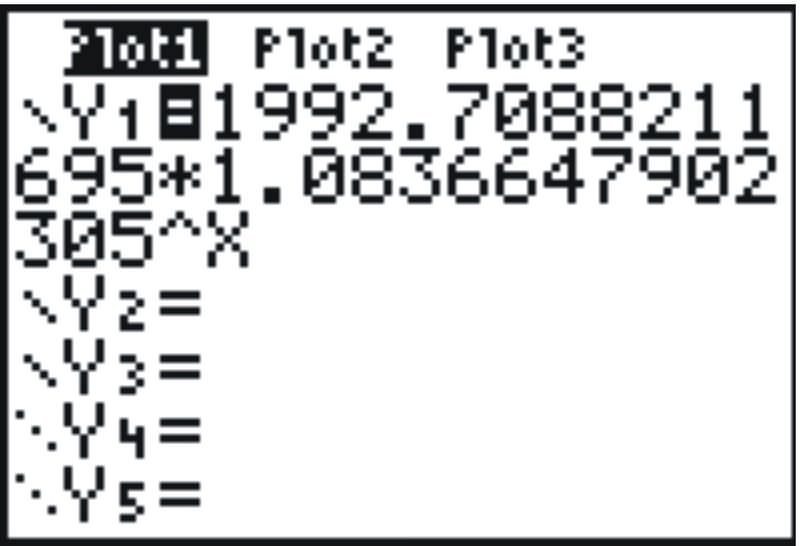
Enter the above rounded-off equation in Y1, or use the following procedure to get the full equation from the calculator: put the cursor in Y1, press , 5, EQ, and 1. This should place the equation in Y1 (see figure below).
::在Y1中输入以上四舍五入方程式,或使用以下程序从计算器中获取全部方程式:将光标放在Y1、按下、5、EQ和1中,这应该将方程式放在Y1中(见下图)。

Now press [STAT PLOT] and complete the items as shown in the figure below.
::现在按下[STAT PLOT],完成下图所示的项目。

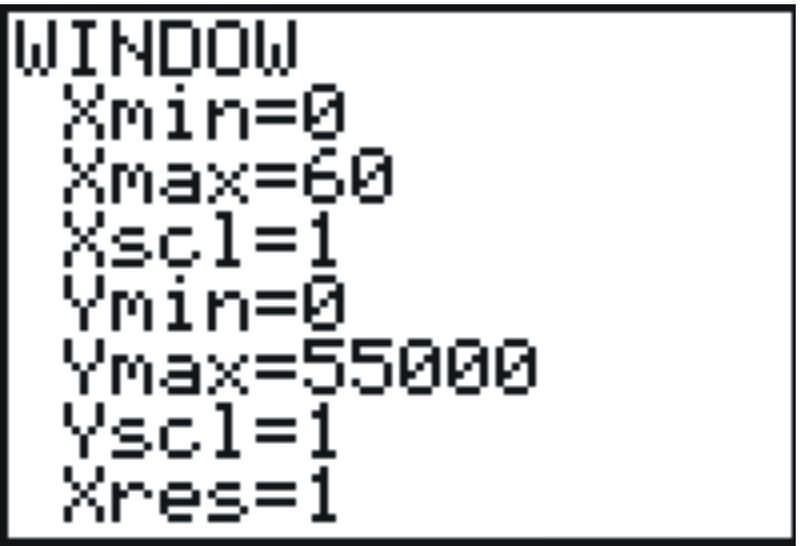
Now set your window. (Hint: use the range of the data to choose the window – the figure below shows our choices.)
::现在设置窗口。 (提示: 使用数据范围选择窗口 - 下图显示我们的选择。 )

Press and you will to see the function and the data points as shown in the figure below.
::按下键可以看到下图中显示的函数和数据点。

Comparing the real data with the modeled results
::将实际数据与模拟结果进行比较

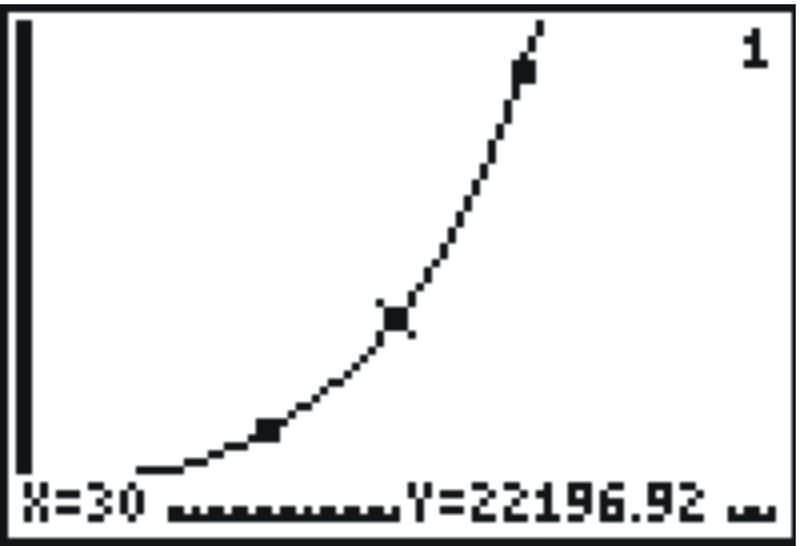
It looks as if the data points lie on the function. However, using the TRACE function you can determine how close the modeled points are to the real data. Press to enter the TRACE mode. Then press the right arrow to move from one data point to another. Do this until you land on the point with value Y=22000. To see the corresponding modeled value, press the up or down arrow. See the figure below. The modeled value is approximately 22197, which is quite close to the actual data. You can verify any of the other data points using the same method.
::它看起来像数据点位于函数上。但是, 使用 TRACE 函数, 您可以确定模型点与真实数据之间的距离。按键可以输入 TRACE 模式。然后按右箭头可以从一个数据点移动到另一个数据点。这样做直到您在值为 Y= 2000 的点上着陆。查看相应的模型值, 按上向或下向箭头。下向或上向箭头。参见下图。模型值约为 22197, 与实际数据相当接近。您可以使用同样的方法验证其他任何数据点。

Example 4
::例4

Tiny Town, CO, currently (year 2012) has a population of 26 people, but it is growing at a rate of 17% per year.
::目前(2012年),总公司小城人口为26人,但年增长率为17%。

Recall from the lesson that the simplified function for population growth is $\begin{align*}P_f = P_i \cdot r^t\end{align*}$ Where " P _f " is final population, " P _i " is initial (starting) population, " r " is growth rate, and " t " is time (in years).
::“Pf”是最终人口,“Pi”是初始(起始)人口,“r”是增长率,“t”是时间(年)。

What is the growth factor for Tiny Town?
::小城的增长因素是什么?

The growth factor is 1.17, since the population each year is the entire population from the year before: $\begin{align*}1 \cdot P\end{align*}$ added to the new population: $\begin{align*}.17 \cdot P\end{align*}$ .
::增长系数为1.17,因为从前一年开始,每年的人口是全部人口,1 加上新的人口:1.17-P。

What will the population be in 2030?
::2030年人口将是什么?

The population in 2030 will be apx 375:
::2030年的人口将达到375阿先令:

$\begin{align*}P_f = 26 \cdot 1.17^17\end{align*}$
::Pf=261.171717

$\begin{align*}P_f = 26 \cdot 14.426\end{align*}$
::Pf=2614.426

$\begin{align*}P_f = 375\end{align*}$
::Pf=375

Example 5
::例5

Abbi invests $4000 in a savings account with an APR of 6.5% compounded yearly.
::阿比比公司在一个储蓄账户投资4 000美元,每年增加6.5%的复兴共和军储蓄账户。

Abbi's money can be calculated with the same type of formula as above: $\begin{align*}A = P \cdot r^t\end{align*}$ Where " A " is final Amount, "'P " is principal (starting money), " r " is growth rate (interest), and " t " is time (in years).
::A=Pirt Where“A”是最终数额,“P”是本金(启动资金),“r”是增长率(利息),“t”是时间(年)。

How much will she have after 2 years?
::两年后她能吃多少?

After 2 years, Abbi will have apx $4500
::两年后,阿比有4500美元

$\begin{align*}A = \$4000 \cdot 1.065^2\end{align*}$
::A=4000-1.0652澳元

$\begin{align*}A = \$4000 \cdot 1.134\end{align*}$
::A=4000-1.1334美元

$\begin{align*}A = \$4536\end{align*}$
::A=4536美元

How much will she have after 15 years?
::15年后她要多少钱?

After 15 years, Abbi will have apx $10,300
::15年后,Abbi将拥有10 300美元的Apx10 300美元

$\begin{align*}A = \$4000 \cdot 1.065^15\end{align*}$
::A=4000-1.06515美元

$\begin{align*}A = \$4000 \cdot 2.5718\end{align*}$
::A=4 000002.5718美元

$\begin{align*}A = \$10287.20\end{align*}$
::A=10287.20美元

How many years will it take to reach $50,000?
::需要多少年才能达到5万美元?

To calculate how long it will take to reach $50,000, we use the formula with $\begin{align*}A = \$50,000\end{align*}$ and $\begin{align*}x\end{align*}$ (in the exponent) is the number of years.
::为了计算达到50 000美元需要多长时间,我们使用A=50 000美元的公式,x(指数)是年数。

$\begin{align*}\$50,000 = \$4000 \cdot 1.065^x\end{align*}$
::50 000美元=4 0000.00 1.065美元

$\begin{align*}12.5 = 1.065^x\end{align*}$ : Divide both sides by $4000
::12.5=1.065x:将双方除以4 000美元

$\begin{align*}log 12.5 = log 1.065^x\end{align*}$ : Take the log of both sides
::log12.5=log1.065x : 使用两侧的日志

$\begin{align*}log 12.5 = xlog 1.065\end{align*}$ : Using $\begin{align*}log x^y = ylog x\end{align*}$ from prior lesson
::log12.5 =xlog1.065 : 使用上一个课程的logxy=ylogx

$\begin{align*}\frac{log 12.5}{log 1.065} = x\end{align*}$ : Divide both sides by $\begin{align*}log 1.065\end{align*}$
::log12.5log1.065=x: 将两边除以 log1.065

$\begin{align*}\frac{1.096}{.0273} = x\end{align*}$ : With a calculator
::1.096.0273=x:使用计算器

$\begin{align*}40.14 = x\end{align*}$ : With a calculator
::40.14=x:使用计算器

It will take just over 40 years for Abbi's initial $4000 to become $50,000 at 6.5% interest compounded yearly.
::Abbi最初的4000美元需要40多年才能以每年6.5%的利息加起来成为50 000美元。

Example 6
::例6

Brandon bought a new car for $30,000. It wasn't until he drove away that his friend Kyle mentioned that the car was going to depreciate at a rate of 50% per year!
::布兰登花了30,000美元买了一辆新车。直到他开车离开,他的朋友凯尔才提到汽车每年以50%的速率贬值!

The formula for calculating decay is again very similar: $\begin{align*}V_f = V_i \cdot r^t\end{align*}$ Where " V _f " is final value, " V _i " is initial value, " r " is decay factor (depreciation rate), and " t " is time (in years).
::计算衰变的公式也非常相似:Vf=Viärt,“Vf”是最终值,“Vi”是初始值,“r”是衰变系数(折旧率),“t”是时间(年)。

What is the decay factor of the car?
::车的衰变因子是什么?

The decay rate is simply $\begin{align*}1 - .5 = .5\end{align*}$ since the car's value decays at a rate of 50% per year.
::衰变率仅为1--5=.5,因为汽车的价值每年以50%的速度衰减。

How much will the car be worth in 5 years?
::5年内这辆车值多少钱?

In 5 years, the car will be worth apx
::5年后,这辆车就值了

$\begin{align*}V_f = \$30,000 \cdot .5^5\end{align*}$
::Vf = 30 000 .55美元

$\begin{align*}V_f = \$30,000 \cdot .03125\end{align*}$
::Vf = 30 000 .03125美元

$\begin{align*}V_f = \$937.50\end{align*}$ OUCH!
::折合937.50美元!

Using your calculation from "b", apx how long will it take before the car is only worth $100?
::用你从"b"Apx的计算法汽车只值100美元需要多久?

If the car loses 1/2 of its value each year, and it is worth apx $1000 after 5 years:
::如果汽车每年损失价值的1/2, 5年后价值1000美元:

Year 6 = $\begin{align*}\$1000 \cdot .5 = \$500\end{align*}$
::6年=100美元=500美元

Year 7 = $\begin{align*}\$500 \cdot .5 = \$250\end{align*}$
::7年=500元=250美元

Year 8 = $\begin{align*}\$250 \cdot .5 = \$125\end{align*}$
::8年=250美元=125美元

It will take only about 8 years before the car is only worth $100. Brandon may have made a questionable purchase!
::这辆车只要100美元就花不了8年了布兰登可能买的货有问题!

Review
::回顾

Calculate the following values using: $\begin{align*}A = P \cdot r^t\end{align*}$
::使用以下值计算 : A=Prt

Assume all rates are x% per year, compounded yearly unless specified otherwise
::假定所有费率均为每年x%,除非另有说明,每年复数

What is the value of a $5000 investment after 5 years at a rate of 5% ?
::5年后投资5000美元的价值是多少? 5%?

What is the value of a $15000 investment after 3 years at a rate of 8% ?
::3年后投资1500美元的价值是多少? 利率为8%?

What is the value of a $3500 investment after 12 years at a rate of 2% ?
::12年后投资3500美元的价值是多少? 利率为2%?

What is the value of a $7550 investment after 7 years at a rate of 4.3% ?
::7年后投资7 550美元的价值是多少? 利率为4.3%?

What is the value of a $42,340 investment after 13 years at a rate of 5.034% ?
::13年后投资42 340美元的价值是多少? 利率为5.034%?

For question s 6-10, calculate:
::对于问题6-10,计算:

The growth factor
::增长因数

The final population
::最后人口

If a population starts at 5,000 people in 1995, and increases at a rate of 7% per year, what is the population in 2032?
::如果1995年人口开始为5,000人,年增长率为7%,那么2032年的人口是多少?

If a population starts at 15,000 people in 2000, and increases at a rate of 3% per year, what is the population in 2027?
::如果2000年人口开始为15 000人,年增长率为3%,那么2027年的人口是多少?

If a population starts at 25,500 people in 1900, and increases at a rate of 2% per year, what is the population in 2008?
::如果人口始于1900年的25,500人,以每年2%的速度增长,那么2008年的人口是多少?

If a population starts at 87,432 people in 1940, and increases at a rate of 4.3% per year, what is the population in 2040?
::如果人口始于1940年的87 432人,年增长率为4.3%,那么2040年的人口是多少?

If a population starts at 126,352 people in 1776, and increases at a rate of 1.067% per year, what is the population in 2012?
::如果1776年人口开始时为126,352人,每年增长率为1.067%,那么2012年的人口是多少?

For questions 11-15, calculate:
::对于问题11-15,计算:

The decay factor (recall that decay factor = 1 - %decay as a decimal)
::衰变系数(提醒注意衰变系数 = 1 - % 以小数计的衰减系数)

The final value, using $\begin{align*}V_f = V_i \cdot r^t\end{align*}$ from the lesson. (Round your answer to the nearest dollar)
::最后值, 使用 Vf= Vif= Viärt 从课程中得出。 (按最接近的美元回答)

A car is worth $4000, and loses value at a rate of 12% per year, what will it be worth in 5 years?
::一辆汽车价值4000美元,每年以12%的速率损失价值,5年内价值多少?

A boat is purchased for $14,000, and loses value at a rate of 16% per year, what will it be worth in 7 years?
::一艘船以14 000美元购买,每年损失16%,7年内价值多少?

A car is purchased for $40,500, and loses value at a rate of 21% per year, what will it be worth in 4 years?
::一辆汽车以40,500美元的价格购买,每年以21%的速度损失价值,四年内价值多少?

A motorcycle is worth $9350, and loses value at a rate of 6.5% per year, what will it be worth in 3.5 years?
::一辆摩托车价值9 350美元,每年损失6.5%,在3.5年中价值多少?

A plane is purchased for $342,137, and loses value at a rate of 4.67% per year, what will it be worth in 13 years?
::以342,137美元购买一架飞机,每年损失4.67%,13年内价值多少?

For questions 16-20, calculate the number of years required before the value reaches the specified total, using $\begin{align*}A_f = A_i \cdot r^t\end{align*}$ and beginning with $\begin{align*}A_f =\end{align*}$ final amount, and $\begin{align*}x\end{align*}$ (in the exponent) as the number of years.
::对于问题16-20,使用Af=Aiirt,从Af=最终数额开始,以x(指数)作为年数,计算数值达到规定总数之前所需的年数。

How many years before a population of 5,000 reaches at least 8,000 at a growth rate of 6%?
::五千人口以6%的增长率至少达到八千人,

How many years before a value of $4,000 reaches at least $7,000 at a growth rate of 4%?
::4 000美元的价值以4%的增长率至少达到7 000美元?

How many years before a value of $12,000 reaches at least $25,000 at a growth rate of 12%?
::12 000美元的价值以12%的增长率至少达到25 000美元?

How many years before a population of 15,500 reaches at least 46,000 at a growth rate of 8.5%?
::15,500人口以8.5%的增长率至少达到46,000人?

How many years before the value of a car currently worth $52,138 depreciates to at least $8,000 at a depreciation rate of 14.7% ?
::汽车价值目前为52,138美元, 以14.7%的折旧率,

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

指数模型

Exponential Models ::指数模型

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)