Course: 5.1 两维矢量 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

两维矢量

Brian was telling Tanya about his trip across the river earlier that day. If he wanted to be accurate and describe how the current made it very difficult for him to actually drive straight across, how could he clearly show the different forces of the motor on his boat pushing one way and the current pushing another? Specifically, how could he show that the boat was crossing the stream at 35 km/hr, and the current was pushing him downstream at 25 km/hr?
::Brian在那天早些时候告诉Tanya他穿越河流的行程。如果他想准确描述水流如何使得他很难真正直奔河面,那么他怎么能够清楚地显示他船上的发动机驱动力不同,而电流推力不同? 具体地说,他如何能显示船在35公里/小时的横越河面,水流将他推到25公里/小时的下游?

Two-Dimensional Vectors
::两维矢量

Throughout the study of vectors we will be using bold-face type to indicate vector quantities and regular face type for scalar quantities, whether we are using the endpoints of the vector or another variable to represent the vector quantity: AB or r. Another way to symbolize vector quantities is to use letters with arrows over them. For example, physicists use $\begin{aligned} \vec{v} \end{aligned}$ to indicate the velocity of an object.
::在整个矢量研究过程中,我们将使用粗体型表示矢量数量和正脸型,以表示标量,无论我们是使用矢量的端点还是另一个变量来表示矢量数量:AB或r。另一种表示矢量的方法是使用字母和箭头来表示它们。例如,物理学家使用 v来表示一个对象的速度。

Vectors can be represented graphically using an arrow which points from the vector’s initial point to its terminal point. The length of the arrow-shaft represents the magnitude of the vector. The arrowhead identifies the vector’s direction.
::矢量可以用箭头图形表示,箭头指向矢量初始点到终点。箭头的长度代表矢量的大小。箭头指向矢量的方向。

Vectors AB and CD have the same magnitude and the same direction, so we can say that AB = CD , even if they don’t have the same location in space. Vectors AB and EF have the same magnitude, but they have opposite directions, therefore EF = – AB . The magnitude of a vector is a scalar quantity, which can be symbolized by | AB |, | r | , $\begin{aligned} | \vec{v} | \end{aligned}$ , or v .
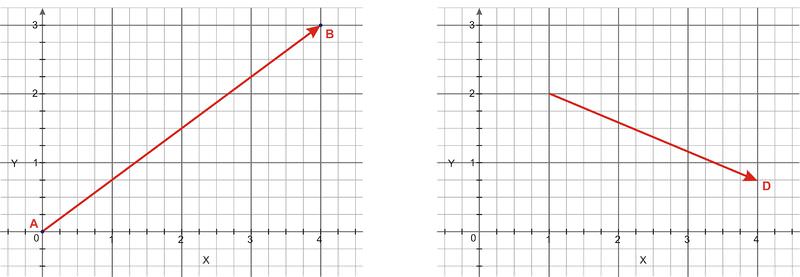
::矢量 AB 和 CD 的大小和方向相同,因此我们可以说 AB = CD, 即使它们在空间中的位置不同。矢量 AB 和 EF 的大小相同, 但方向相反, 因此 EF = - AB。矢量的大小是一个数量级数, 可以用 AB 、、、或 v 表示。

Vectors can also be represented algebraically, using component notation. The components tell us the extent of the vector along the coordinate directions. For example, the vector on the left in the image below has components in both the x -direction, AB _x , and the y-direction, AB _y . Here, AB _x = 4 and AB _y = 3 because point B is 3 units to the right and 3 units up from point A. Similarly, vector D has components D _x = 3 and D _y = –1.25. The negative sign in D _y indicates that the y -component of vector D is downward, in the negative y direction. As with other numbers, we usually only include the negative sign explicitly.
::矢量也可以使用元件标记来表示代数。组件告诉我们坐标方向的矢量范围。例如, 下面图像左侧的矢量在 x 方向、 ABx 和 y 方向、 ABy 中都有组件。这里, ABx = 4 和 ABy = 3, 因为点B 向右是 3 个单位, 从 A点向上是 3 个单位。同样, 矢量 D 含有 Dx = 3 和 Dy = - 1. 25 。 Dy 中的负号表示矢量D 的 Y 向下向, 在负 y 方向。和其他数字一样, 我们通常只明确包含负号。

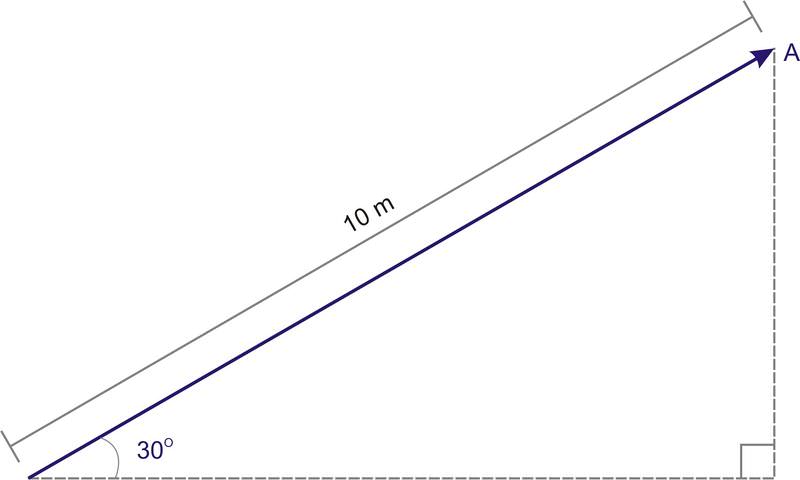
Sometimes bracket notation is used to identify the components of a vector. The components of the vector are written as an ordered set of values, similar to the coordinates of a point in space. For example, vector $\begin{aligned} A B = ⟨ 4, 3 ⟩ \end{aligned}$ and $\begin{aligned} D = ⟨ 3, - 1.25 ⟩ . \end{aligned}$
::有时用括号符号来识别矢量的成分。矢量的成分是按顺序排列的一组数值写成的,类似于空间点的坐标。例如,矢量 AB4,3和D3,-1.25。

If the coordinate system is polar rather than rectangular, a vector is identified by its magnitude and its direction with respect to the x -axis (or r -axis). In the case of the vector below, A = 10 m @ 30 ^o .
::如果坐标系为极性而非矩形,则根据矢量的大小及其相对于 x 轴(或 r 轴) 的方向确定矢量。对于以下的矢量,A = 10 m@ 30o。

The process of determining the components of a vector is also known as resolving the vector. For example, if we wish to convert the radial coordinate notation for vector A into rectangular coordinates, we can use right triangle trigonometry to resolve the vector. First, create a right triangle with the vector as the hypotenuse and with the two legs of the triangle parallel to the rectangular coordinate axes. Then, according to the definitions of sine and cosine, A _x = | A | cos 30 and A _y = | A | sin 30.
::确定矢量组件的过程也称为解析矢量。例如,如果我们想将矢量 A 的弧坐标符号转换为矩形坐标,我们可以使用右三角三角三角三角测量来解析矢量。首先,以矢量为下限,用三角的两腿与矩形坐标轴平行,建立一个右三角三角。然后,根据正弦和正弦的定义,Ax = A = = = = = = = = = = = = = spin 30 和 A = = spin 30 。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Brian and the different forces acting on his boat.
::早些时候,你得到一个问题关于布莱恩和不同的力量在他的船上行动。

If a boat is being motored perpendicularly at 35km/hr across a stream which is flowing at 25km/hr, how can the direction and speed that it travels be clearly shown using vectors?
::如果一艘船舶在每小时35公里处经过25公里/小时流动的溪流以直径35公里/小时的机动,如何用矢量清楚地显示其行驶的方向和速度?

There are a number of possible notations, one example is:
::有一些可能的标记,例如:

In vector notation, the x component is 30 units, and the y component is 25 units.
::在矢量标记方面,x部分为30个单位,y部分为25个单位。

$\begin{aligned} ∴ A B = ⟨ 30, 25 ⟩ \end{aligned}$
::AB30,25

Brian could also draw a diagram and represent the speed of the boat with an arrow 35units long, and the current with an arrow 25units long.
::Brian还可以绘制一个图表,用一条35毫米长的箭头代表船只的速度,用一条25毫米长的箭头代表洋流。

Example 2
::例2

Express the statements in your own words:
::以你的话语表示:

$\begin{aligned} A B_{x} = C D_{x} : A B_{y} = - C D_{y} \end{aligned}$
::ABx=CDx:AByCDy

Vector AB component x is equal to vector CD component x , AB component y is the same magnitude as CD component y , but in the opposite direction.
::矢量 AB 元件轴等于矢量 CD 元件x, AB 元件与 CD 元件相同, 但方向相反。

Vector $\begin{aligned} A B = ⟨ 4, 6 ⟩ \end{aligned}$
::矢量 AB4,6

Vector AB has x component of 4 units, and y component of 6 units.
::矢量 AB 包含 x 的 4 个元件, Y 的 6 个元件。

Example 3
::例3

What are the x and y components of the vectors shown in the diagram?
::图中显示的矢量的 x 和 Y 组件是什么 ?

	AB	CD	EF	GH	IJ	KL	MN
x - component	2.25	-1.5	0	-1.5	2.0	1.5	-2.25
y - component	0.25	-2.0	-2.25	-2.0	-1.5	2.0	0

In the diagram, each division is 0.25 units. All vectors which point toward the left have negative x -components and those that point downward have negative y-components. Notice that for the horizontal vector, MN , the y-component is equal to 0. Likewise, for the vertical vector, EF , the x -component is equal to 0.
::在图表中,每个区域为0.25个单位。所有向左点的矢量都有负 x 构件,向下点的矢量有负 Y 构件。请注意,对于水平矢量, MN, Y 构件等于 0。同样,对于垂直矢量, EF, x 构件等于 0。

Example 4
::例4

Which of the vectors in Example 3 is equal to vector CD ?
::例3中的哪个矢量等于矢量 CD ?

Vector GH = CD. Both vectors have the same length and the same orientation.
::矢量=CD。这两种矢量的长度相同,方向相同。

Which vector is equal to –CD ?
::哪个矢量等于-CD ?

Vector KL = –CD . Both vectors have the same length and the two vectors point in opposite directions.
::矢量 KL =- CD。两种矢量的长度相同,而两种矢量的方向相反。

Example 5
::例5

For the two vectors $\begin{aligned} \vec{A} \end{aligned}$ and $\begin{aligned} \vec{B} \end{aligned}$ shown in the diagram, determine the components, magnitude, and orientation angle for vector $\begin{aligned} \vec{C} = \vec{A} + \vec{B} \end{aligned}$ .
::对于图表中显示的两个矢量 A 和 B ,确定矢量 C 和 A 和 B 的成分、数量和方向角。

As we saw in the previous problem, $\begin{aligned} \vec{A} = ⟨ 4.75, 0.5 ⟩ \end{aligned}$ and $\begin{aligned} \vec{B} = ⟨ - 2.25, - 3.5 ⟩ \end{aligned}$ . To add the two vectors, we add the x-components together and we add the y-components together to give $\begin{aligned} \vec{C} = ⟨ (4.75 + (- 2.25)), (- 3.5 + 0.5) ⟩ = ⟨ 2.5, - 3 ⟩ \end{aligned}$
::正如我们在前一个问题(A4.75,0.5和B2.25,-3.5)中看到的那样,在添加两个矢量时,我们将 x 构件加在一起,将y 构件加在一起,给C(4.75+(-2.25)),(3.5+0.5) 2.5,-3 。

We can also add these two vectors graphically by positioning $\begin{aligned} \vec{A} \end{aligned}$ and $\begin{aligned} \vec{B} \end{aligned}$ head to tail. Vector $\begin{aligned} \vec{A} \end{aligned}$ is the single vector that begins where $\begin{aligned} \vec{A} \end{aligned}$ begins and ends where $\begin{aligned} \vec{B} \end{aligned}$ ends. As you can see from the diagram, the components of vector $\begin{aligned} \vec{C} \end{aligned}$ are $\begin{aligned} C_{x} = 2.5 \end{aligned}$ and $\begin{aligned} C_{y} = - 3 \end{aligned}$ .
::也可以用图形方式将这两个矢量添加到尾部, 将 A 和 B 和 B 分别定位为 A 和 B 和 B 和 B 。矢量 A 是 A 开始和 B 结束的单一矢量。从图表中可以看到, 矢量 C 的成分是 Cx= 2.5 和 Cy 3 。

Example 6
::例6

$\begin{aligned} \vec{A} = ⟨ 12, 7, 9.5 ⟩ \end{aligned}$ and $\begin{aligned} \vec{B} = ⟨ 8, 8, 11 ⟩ \end{aligned}$ Determine the vector $\begin{aligned} \vec{C} \end{aligned}$ that makes the following equation true: $\begin{aligned} \vec{A} + \frac{1}{2} \vec{C} = \frac{2}{5} \vec{B} \end{aligned}$ .
::A*12,7,9.5和B8,8,11确定矢量C,使以下等式成为事实:A12C25B。

Use standard algebraic techniques to solve for $\begin{aligned} \vec{C} \end{aligned}$ :
::使用标准的代数技术解析 C:

$\begin{aligned} \frac{1}{2} \vec{C} = \frac{2}{5} \vec{B} - \vec{A} \end{aligned}$
::12C25BA__A____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} \vec{C} = \frac{4}{5} \vec{B} - 2 \vec{A} \end{aligned}$
::45B2A

Remember that multiplying a vector by a scalar means multiplying each of the vector’s components by that vector. Therefore,
::记住,将矢量乘以一个星标意味着将矢量的每个组成部分乘以该矢量。因此,

$\begin{aligned} \frac{4}{5} \vec{B} = ⟨ (\frac{4}{5} * 8), (\frac{4}{5} * 8), (\frac{4}{5} * 11) ⟩ = ⟨ (\frac{32}{5}), (\frac{32}{5}), (\frac{44}{5}) ⟩ = ⟨ 6.4, 6.4, 8.8 ⟩ \end{aligned}$
::45B*(45*),(45*8),(45*8),(45*11),(325),(325),(445),(6.4),(6.4),(8.8)

$\begin{aligned} 2 \vec{A} = ⟨ (2 * 12), (2 * 7), (2 * 9.5) ⟩ = ⟨ 24, 14, 19 ⟩ \end{aligned}$
::2A*(2**12),(2*7),(2*9.5) 24,14,19

Therefore
::因此,

$\begin{aligned} \vec{C} = ⟨ (6.4 - 24), (6.4 - 14), (8.8 - 19) ⟩ = ⟨ - 17.6, - 7.6, - 10.2 ⟩ \end{aligned}$
::C*(6.4-24),(6.4-14),(8.8-19),(17.6),(7.6)-(10.2)

Example 7
::例7

A vector can be written as $\begin{aligned} \vec{R} = 2.74 m \end{aligned}$ @ $\begin{aligned} 60^{\circ} \end{aligned}$ . Identify this same vector using component notation.
::矢量可以写成 R2. 74m@ 60 。使用元件标记来识别相同的矢量。

When resolving a two-dimensional vector into components, remember that the vector itself is always the hypotenuse of a right triangle. If we define the x-axis as pointing from the origin along θ = 0 ^o and the y-axis as pointing along θ = 90 ^o , the x-component is given by R _x = R cos θ and R _y = R sin θ . In this case,
::当将二维矢量溶解为元件时,请记住矢量本身始终是右三角形的下限。如果我们将 X 轴定义为以 = 0o 和 Y 轴为源点,以 = = 90o为源点,则X 元由 Rx = R cos 和 Ry = R sin 提供。在这种情况下,

R _x = R cos θ = (2.74m) cos 60 ^o = 1.37m
::Rx = R = R = R cos = = (2.74米) = (60o = 1.37米)

R _y = R sin θ = (2.74m) sin 60 ^o = 2.37m
::Ry = R sin = (2.74米) sin 60o = 2.37米

Review
::回顾

Can the x or y component of a vector ever have a greater magnitude than the vector itself?
::矢量的 x 或 Y 组件是否比矢量本身具有更大的规模?

If two vectors have magnitudes that are not equal, can the sums of their magnitudes ever be zero?
::如果两个矢量的量值不相等,那么其量值的总和是否为零?

Using the Cartesian coordinate system, draw the vectors.
::使用笛卡尔坐标系统,绘制矢量。

$\begin{aligned} A = 1 x + 2 y \end{aligned}$
::A=1x+2y

$\begin{aligned} B = - 2 x + 2 y \end{aligned}$
::B2x+2y

$\begin{aligned} C = - 2 x - 3 y \end{aligned}$
::C2x-3y

Identify and plot the three angles, (a,b,c) to describe the direction of each vector.
::确定并绘制三个角度(a、b、c),以描述每个矢量的方向。

Calculate the magnitude and angles of each vector.
::计算每个矢量的大小和角度。

$\begin{aligned} A = 1 x + 2 y \end{aligned}$
1. Magnitude:
  ::磁度 :
2. Angle:
  ::角度 :
::A=1x+2y 磁度: 角度 :

$\begin{aligned} B = - 2 x + 2 y \end{aligned}$
1. Magnitude:
  ::磁度 :
2. Angle:
  ::角度 :
::B2x+2y 磁度: 角度 :

$\begin{aligned} C = - 2 x - 3 y \end{aligned}$
1. Magnitude:
  ::磁度 :
2. Angle:
  ::角度 :
::C2x-3y 磁度: 角度 :

Describe and sketch the set of all points (x, y) in that satisfy:
::描述和勾画符合以下条件的所有点数组(x, y):

$\begin{aligned} x = y \end{aligned}$
::x=y x=y

$\begin{aligned} x + y = 1 \end{aligned}$
::x+y=1 x+y=1

$\begin{aligned} x^{2} + y^{2} = 4 \end{aligned}$
::x2+y2=4 x2+y2=4

$\begin{aligned} x^{2} + y^{2} = 2 y \end{aligned}$
::x2+y2=2y

Identify the vectors using component notation.
::使用组件符号识别矢量。

A vector can be written as $\begin{aligned} \vec{R} = 3.45 m \end{aligned}$ @ $\begin{aligned} 170^{\circ} \end{aligned}$ .
::矢量可以写成 R3. 45m@ 170。

A vector can be written as $\begin{aligned} \vec{R} = 11 m \end{aligned}$ @ $\begin{aligned} 90^{\circ} \end{aligned}$ .
::矢量可以写为 R11m@ 90。

A vector can be written as $\begin{aligned} \vec{R} = 7.23 m \end{aligned}$ @ $\begin{aligned} 45^{\circ} \end{aligned}$ .
::矢量可以写成 R7. 23m@ 45.

A vector can be written as $\begin{aligned} \vec{R} = 2.7 m \end{aligned}$ @ $\begin{aligned} 235^{\circ} \end{aligned}$ .
::矢量可以写成 R2. 7m@ 235@ 235_ 。

A vector can be written as $\begin{aligned} \vec{R} = 23.75 m \end{aligned}$ @ $\begin{aligned} 255^{\circ} \end{aligned}$ .
::矢量可以写成 R23. 75m@ 255_ @ 255_ 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

两维矢量

Two-Dimensional Vectors ::两维矢量

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)