Course: 13.2 松, 脊弦, 唐恩特

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 顺弦、顺弦、正弦

Collapse Expand
顺弦、顺弦、正弦
An isosceles right triangle has leg lengths of 4 units each. What is the sine of each of the triangle's acute angles?
::右三角形的等离子体每条腿长为4个单位。三角形的急性角的正弦值是多少?

Sine, Cosine and Tangent
::顺弦、顺弦和唐敏

The trigonometric ratios sine, cosine and tangent refer to the known ratios between particular sides in a right triangle based on an acute angle measure.
::三角正弦、正弦和正切比例是指以急性角测量为基础的右三角中特定方之间已知的比率。

In this right triangle, side $\begin{aligned} c \end{aligned}$ is the hypotenuse.
::在右三角形中,C侧为下限。

If we consider the angle $\begin{aligned} B \end{aligned}$ , then we can describe each of the legs by its position relative to angle $\begin{aligned} B \end{aligned}$ : side $\begin{aligned} a \end{aligned}$ is adjacent to $\begin{aligned} B \end{aligned}$ ; side $\begin{aligned} b \end{aligned}$ is opposite $\begin{aligned} B \end{aligned}$
::如果我们考虑角度B,那么我们可以根据每一腿与角度B相对的位置来描述每一腿:一方a与B相邻;另一方b在B对面。

If we consider the angle $\begin{aligned} A \end{aligned}$ , then we can describe each of the legs by its position relative to angle $\begin{aligned} A \end{aligned}$ : side $\begin{aligned} b \end{aligned}$ is adjacent to $\begin{aligned} A \end{aligned}$ ; side $\begin{aligned} a \end{aligned}$ is opposite $\begin{aligned} A \end{aligned}$
::如果我们考虑A角度,那么我们可以用与A角度相对的位置来描述每条腿:A:B侧与A相邻;A对面是A侧;A对面是A侧;A对面是A侧;A对面是A侧;A对面是A方;A对面是A方;A对面是A方;A对面是A方。

Now we can define the trigonometry ratios as follows:
::现在,我们可以将三角测量比率定义如下:

$\begin{aligned} S i n e i s \frac{o p p o s i t e}{h y p o t e n u s e} C o s i n e i s \frac{a d j a c e n t}{h y p o t e n u s e} T a n g e n t i s \frac{o p p o s i t e}{a d j a c e n t} \end{aligned}$

::相邻的相邻的相邻的相邻相邻的相邻

A shorthand way to remember these ratios is to take the letters in red above and write the phrase:
::记住这些比率的捷径是,用上面的红色字母来写:

$\begin{aligned} S O H C A H T O A \end{aligned}$

::高山太地

Now we can find the trigonometric ratios for each of the acute angles in the triangle above.
::现在我们可以找到三角形上三角形每个急性角的三角比

$\begin{aligned} \sin A & = \frac{a}{c} \sin B = \frac{b}{c} \\ \cos A & = \frac{b}{c} \cos B = \frac{a}{c} \\ \tan A & = \frac{a}{b} \tan B = \frac{b}{a} \end{aligned}$

::A=absinB=bccosA=bccosB=actanA=abtanB=ba

It is important to understand that given a particular (acute) angle measure in a right triangle, these ratios are constant no matter how big or small the triangle. For example, if the measure of the angle is $\begin{aligned} 25^{\circ} \end{aligned}$ , then $\begin{aligned} \sin 25^{\circ} \approx 0.4226 \end{aligned}$ and ratio of the opposite side to the hypotenuse is always 0.4226 no matter how big or small the triangle.
::重要的是要理解,根据右三角形中特定(急性)角度的测量,这些比例无论三角形大小大小都是不变的。例如,如果角的测量值是 25 ,那么则sin25 0.4226 和对面的比值总是 0.4226, 不论三角形大小。

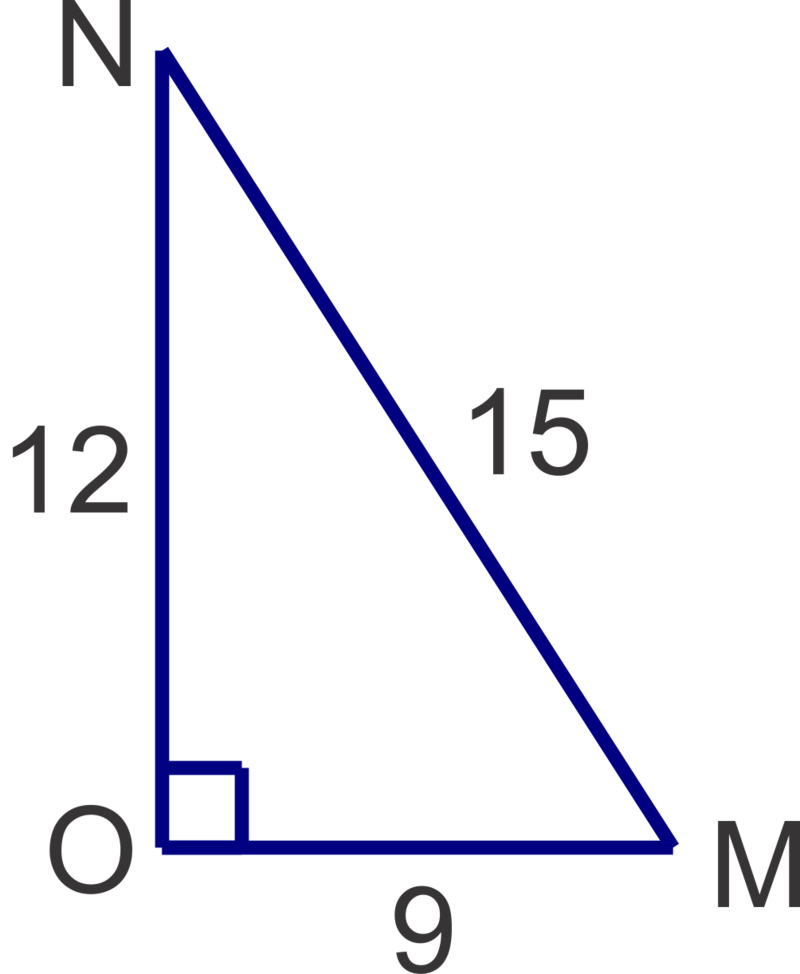
Let's find the trig ratios for the acute angles $\begin{aligned} R \end{aligned}$ and $\begin{aligned} P \end{aligned}$ in $\begin{aligned} Δ P Q R \end{aligned}$ .
::让我们在 QPQR 中找到急性角R和P的三角比。

From angle $\begin{aligned} R \end{aligned}$ , $\begin{aligned} O = 8 \end{aligned}$ ; $\begin{aligned} A = 15 \end{aligned}$ ; and $\begin{aligned} H = 17 \end{aligned}$ . Now the trig ratios are:
::从角R、O=8、A=15和H=17。现在的三角比率是:

$\begin{aligned} \sin R = \frac{8}{17}; \cos R = \frac{15}{17}; \tan R = \frac{8}{15} \end{aligned}$

::sinR=817; cosR=1517; tanR=815

From angle $\begin{aligned} P \end{aligned}$ , $\begin{aligned} O = 15 \end{aligned}$ ; $\begin{aligned} A = 8 \end{aligned}$ ; and $\begin{aligned} H = 17 \end{aligned}$ . Now the trig ratios are:
::从角P、O=15、A=8和H=17。现在的三角比率是:

$\begin{aligned} \sin P = \frac{15}{17}; \cos P = \frac{8}{17}; \tan P = \frac{15}{8} \end{aligned}$

::sinP=1517; cosP=817; tanP=158

Do you notice any patterns or similarities between the trigonometric ratios? The opposite and adjacent sides are switched and the hypotenuse is the same. Notice how this switch affects the ratios:
::您是否注意到三角比之间有任何模式或相似之处? 相对和相邻的边被切换, 下限相同。注意此开关如何影响比例 :

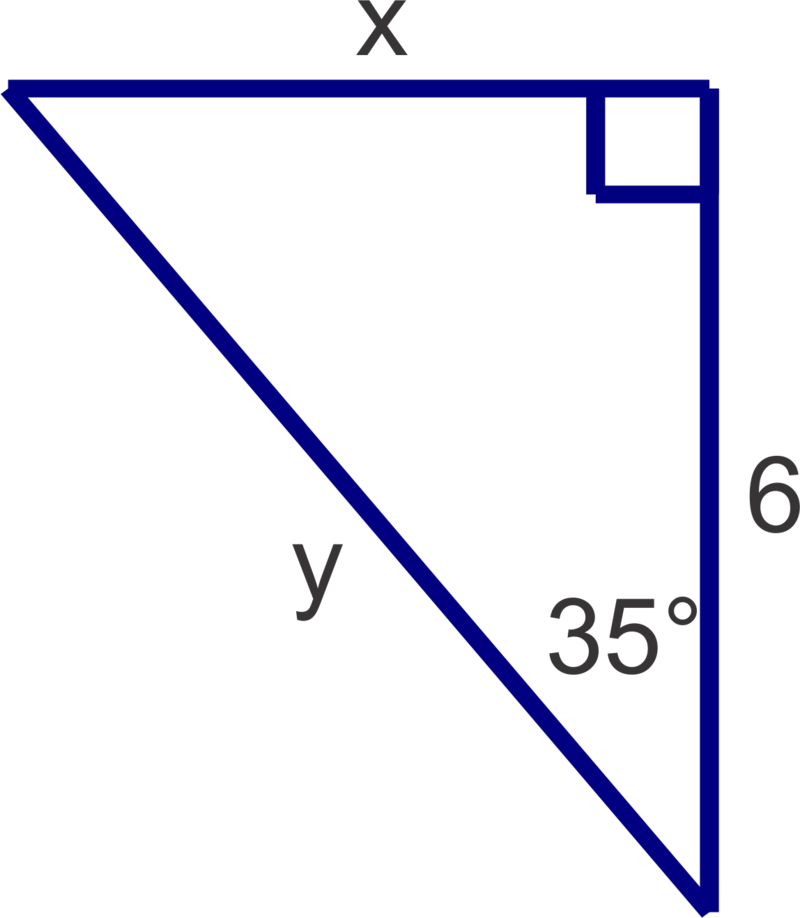
$\begin{aligned} \sin R = \cos P \cos R = \sin P \tan R = \frac{1}{\tan P} \end{aligned}$

::R=cosPcosR=sinPtanR=1tanP

Now, let's use trigonometric ratios to find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::现在,让我们用三角比来找到x和y。

First identify or label the sides with respect to the given acute angle. So, $\begin{aligned} x \end{aligned}$ is opposite, $\begin{aligned} y \end{aligned}$ is hypotenuse (note that it is the hypotenuse because it is the side opposite the right angle, it may be adjacent to the given angle but the hypotenuse cannot be the adjacent side) and 6 is the adjacent side.
::首先识别或标注给定的急性角的侧面。所以, x 是相反的, y 是下限( 注意它是下限, 因为它是右角的对面, 它可能与给定角相邻, 但下限不能是相邻的侧面) , 6 是相邻的侧面。

To find $\begin{aligned} x \end{aligned}$ , we must use the given length of 6 in our ratio too. So we are using opposite and adjacent. Since tangent is the ratio of opposite over adjacent we get:
::要找到 x, 我们也必须在比例中使用给定的 6 长度。所以我们使用相对和相邻的。因为正切是相对比, 我们得到的是 :

$\begin{aligned} \tan 35^{\circ} & = \frac{x}{6} \\ x & = 6 \tan 35^{\circ} multiply both sides by 6 \\ x & \approx 4.20 Use the calculator to evaluate-type in 6TAN(35) ENTER \end{aligned}$

::使用计算器在 6TAN (35) ENTER 中评估类型

NOTE: make sure that your calculator is in DEGREE mode. To check, press the MODE button and verify that DEGREE is highlighted (as opposed to RADIAN). If it is not, use the arrow buttons to go to DEGREE and press ENTER. The default mode is radian, so if your calculator is reset or the memory is cleared it will go back to radian mode until you change it.
::注意 : 请确定您的计算器是 DEGREE 模式。要检查, 请按 MODE 按钮并核实 DEGREE 是否被突出显示( 与 RADIAN 相对)。如果不是, 请使用箭头按钮去 DEGREE 并按 ENTER 键。默认模式是弧度。因此, 如果您的计算器被重设或内存被清除, 它将会返回到弧度模式, 直到您更改它。

To find $\begin{aligned} y \end{aligned}$ using trig ratios and the given length of 6, we have adjacent and hypotenuse so we’ll use cosine:
::使用三重比和六分之六的长度来查找y, 我们有相邻的和下限的, 所以我们会使用余弦:

$\begin{aligned} \cos 35^{\circ} & = \frac{6}{y} \\ \frac{\cos 35^{\circ}}{1} & = \frac{6}{y} set up a proportion to solve for y \\ 6 & = y \cos 35^{\circ} cross multiply \\ y & = \frac{6}{\cos 35^{\circ}} divide by \cos 35^{\circ} \\ y & = 7.32 Use the calculator to evaluate-type in 6/TAN(35) ENTER \end{aligned}$

::在 6/ TAN (35) 中使用计算器来评估类型 6/ TAN (35) ENTER

Alternatively, we could find $\begin{aligned} y \end{aligned}$ using the value we found for $\begin{aligned} x \end{aligned}$ and the :
::或者,我们也可以使用我们为 x 和 :

$\begin{aligned} {4.20}^{2} + 6^{2} & = y^{2} \\ 53.64 & = y^{2} \\ y & \approx 7.32 \end{aligned}$

::4.202+62=y253.64=y2y7.32

The downside of this method is that if we miscalculated our $\begin{aligned} x \end{aligned}$ value, we will double down on our mistake and guarantee an incorrect $\begin{aligned} y \end{aligned}$ value. In general you will help avoid this kind of mistake if you use the given information whenever possible.
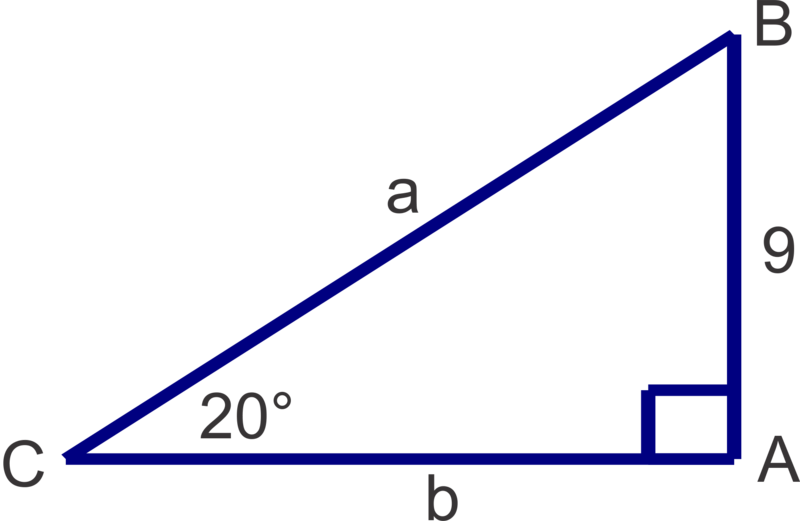
::这种方法的缺点是,如果我们误算了我们的x值,我们就会加倍犯错误,保证不正确的y值。一般来说,如果你尽可能使用给定的信息,你会帮助避免这种错误。

Finally, given $\begin{aligned} Δ A B C \end{aligned}$ , with $\begin{aligned} m ∠ A = 90^{\circ}, m ∠ C = 20^{\circ} \end{aligned}$ and $\begin{aligned} c = 9 \end{aligned}$ , let's find $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ .
::最后,根据 ABC,与mA=90,mC=20和c=9,让我们找a和b。

Visual learners may find it particularly useful to make a sketch of this triangle and label it with the given information:
::视觉学习者可能发现特别有用的是对这一三角形做一个草图,并用给定的信息标出:

To find $\begin{aligned} a \end{aligned}$ (the hypotenuse) we can use the opposite side and the sine ratio: $\begin{aligned} \sin 20^{\circ} = \frac{9}{a} \end{aligned}$ , solving as we did in the previous problem, we get $\begin{aligned} a = \frac{9}{\sin 20^{\circ}} \approx 26.31 \end{aligned}$ . To find $\begin{aligned} b \end{aligned}$ (the adjacent side) we can use the opposite side and the tangent ratio: $\begin{aligned} \tan 20^{\circ} = \frac{9}{b} \end{aligned}$ , solving for $\begin{aligned} b \end{aligned}$ we get $\begin{aligned} b = \frac{9}{\tan 20^{\circ}} \approx 24.73 \end{aligned}$ .
::为了找到一个(顶点),我们可以使用相反的一面和正弦比:sin209a(sin209a),像我们在前一个问题中所做的那样解决,我们得到一个=9sin2026.31。为了找到b(相邻的一面),我们可以使用相反的一面和正弦比:tan209b,解决b(b)我们得到 b=9tan2024.73。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the sine of each of the triangle's acute angles.
::早些时候,你被要求找到三角形每个急性角度的正弦

If you draw the triangle described in this problem, you will see that the sine $\begin{aligned} \frac{o p p o s i t e}{h y p o t e n u s e} \end{aligned}$ of each of the acute angles in the same. It is $\begin{aligned} \frac{4}{h y p o t e n u s e} \end{aligned}$ . So we need to find the hypotenuse.
::如果您绘制了这一问题中描述的三角形, 您就会看到每个急性角度的正反向同步。这是 4 yypotenuse 。所以我们需要找到 potenuse 。

Let's use the Pythagorean Theorem.
::让我们使用毕达哥伦神话

$\begin{aligned} 4^{2} + 4^{2} = c^{2} \\ 16 + 16 = c^{2} \\ 32 = c^{2} \\ c = 4 \sqrt{2} \end{aligned}$

::42+42=c216+16=c232=c2c=42

Therefore, the sine of both of the acute angles is $\begin{aligned} \frac{4}{4 \sqrt{2}} \end{aligned}$ or $\begin{aligned} \frac{\sqrt{2}}{2} \end{aligned}$ .
::因此,两个急性角的正弦值是442或22。

Example 2
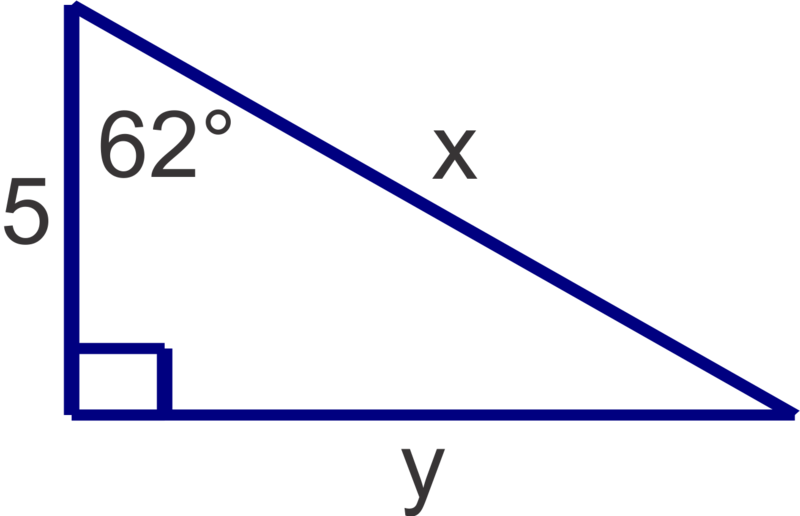
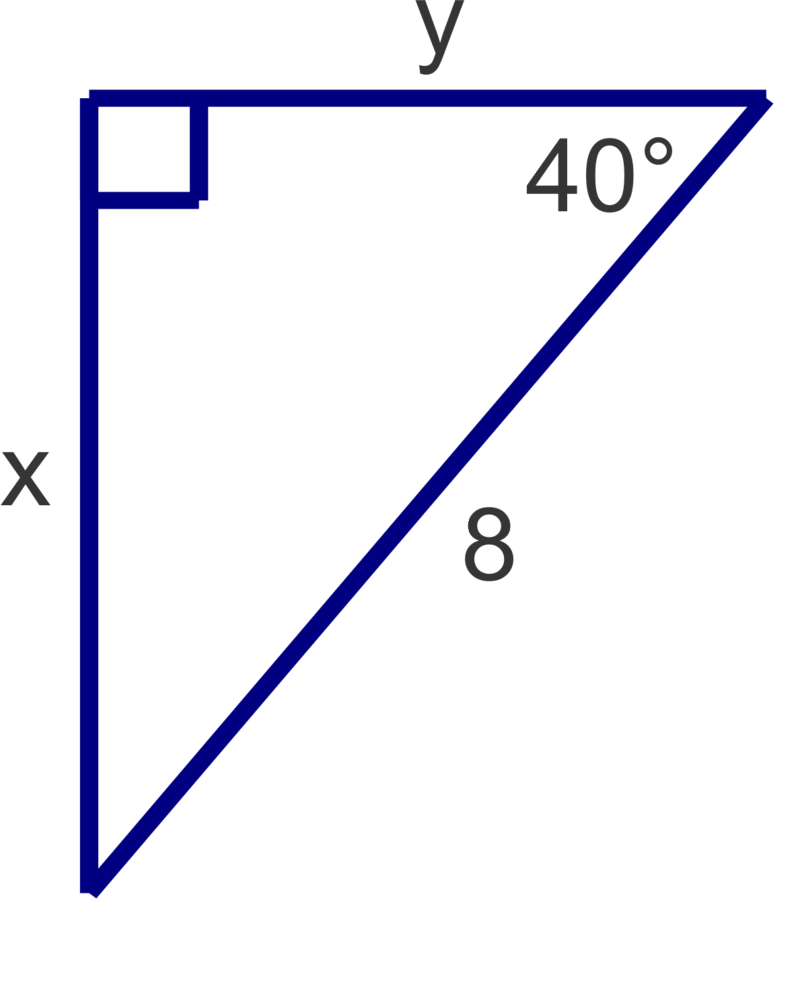
::例2

Use trig ratios to find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ :
::使用 trig 比率查找 x 和 y :

For $\begin{aligned} x \end{aligned}$ :
$\begin{aligned} \cos 62^{\circ} & = \frac{5}{x} \\ x & = \frac{5}{\cos 62^{\circ}} \approx 10.65 \end{aligned}$

::对于 x: cos625xx=5cos6210.65

For $\begin{aligned} y \end{aligned}$ :
$\begin{aligned} \tan 62^{\circ} & = \frac{y}{5} \\ y & = 5 \tan 62^{\circ} \approx 9.40 \end{aligned}$

::y5yy=5tan $62 $9.40

Example 3
::例3

Given $\begin{aligned} Δ A B C \end{aligned}$ with $\begin{aligned} m ∠ B = 90^{\circ}, m ∠ A = 43^{\circ} \end{aligned}$ and $\begin{aligned} a = 7 \end{aligned}$ , find $\begin{aligned} b \end{aligned}$ and $\begin{aligned} c \end{aligned}$ .
::鉴于ABC与mB=90,mA=43和a=7,发现b和c。

For $\begin{aligned} b \end{aligned}$ :
$\begin{aligned} \sin 43^{\circ} & = \frac{7}{b} \\ b & = \frac{7}{\sin 43^{\circ}} \approx 10.26 \end{aligned}$

::对于 b: sin437b=7sin4310.26

For $\begin{aligned} c \end{aligned}$ :
$\begin{aligned} \tan 43^{\circ} & = \frac{7}{c} \\ c & = \frac{7}{\tan 43^{\circ}} \approx 7.51 \end{aligned}$

::c: 对于 c: tann437cc=7tan437.51

Example 4
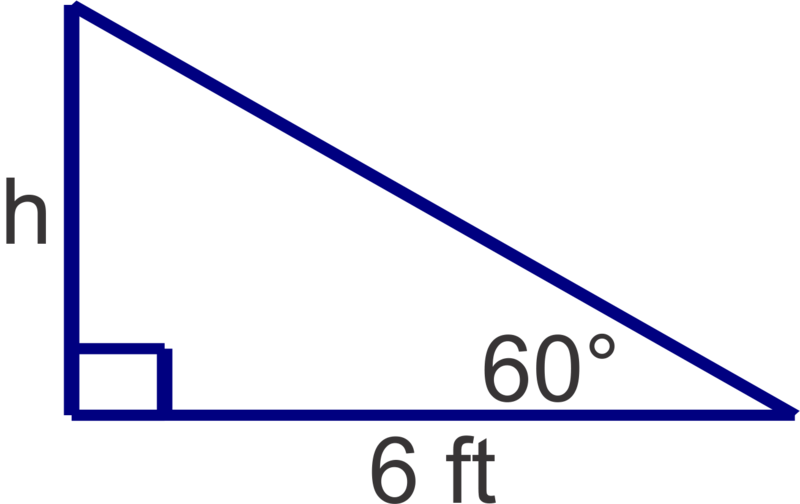
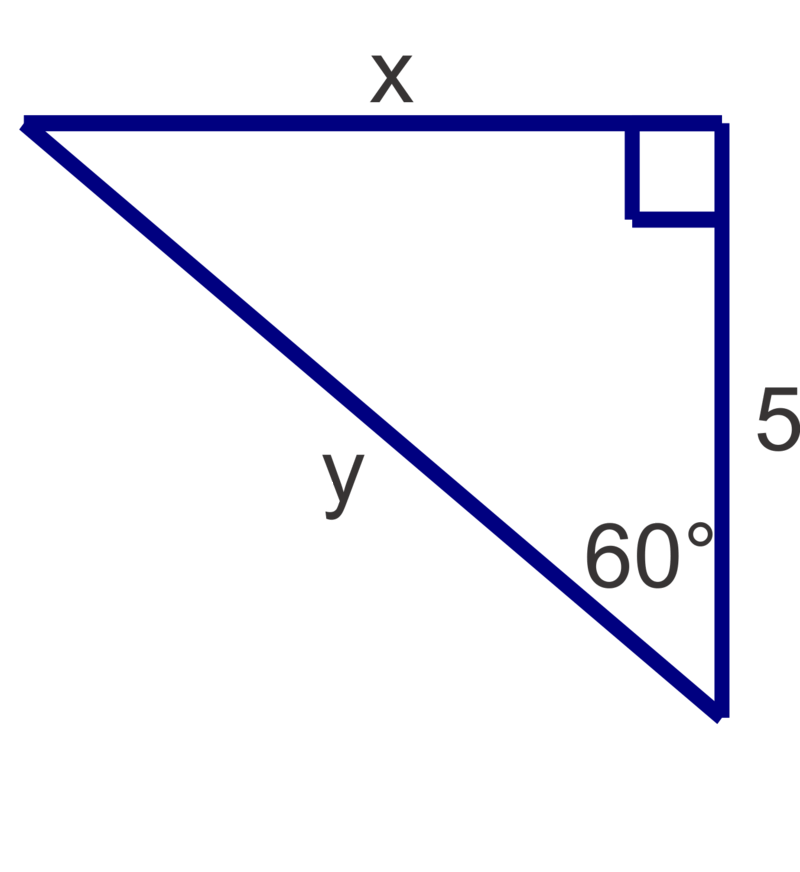
::例4

The base of a playground slide is 6 ft from the base of the platform and the slide makes a $\begin{aligned} 60^{\circ} \end{aligned}$ angle with the ground. To the nearest tenth of a foot, how high is the platform at the top of the slide?
::游乐场幻灯片的底部是平台底部的 6 英尺, 幻灯片的角是60 英寸。到最近的十分之一英尺, 幻灯片顶部的平台有多高 ?

$\begin{aligned} \tan 60^{\circ} & = \frac{h}{6} \\ h & = 6 \tan 60^{\circ} \approx 10.39 \end{aligned}$
So the height of the platform is 10.4 ft.
::60h6h=6tan6010.39 So,平台的高度为10.4英尺。

Review
::回顾

Use you calculator to find the following trigonometric ratios. Give answers to four decimal places.
::使用计算器查找以下三角比。给小数点后四位的答案。

$\begin{aligned} \sin 35^{\circ} \end{aligned}$
::三、三、三、三、一、二、二、四、四、四、四、四、四、四、四、五、五、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、六、七、七、八、八、八、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、十、

$\begin{aligned} \tan 72^{\circ} \end{aligned}$
::

$\begin{aligned} \cos 48^{\circ} \end{aligned}$
::{\pos(192,285)}翻譯: 48 * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

$\begin{aligned} \tan 45^{\circ} \end{aligned}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

$\begin{aligned} \sin 30^{\circ} \end{aligned}$
::问题 30

$\begin{aligned} \cos 88^{\circ} \end{aligned}$
::COS88

Write the three trigonometric ratios of each of the acute angles in the triangle below.
::写下三角形下每个急性角度的三个三角比。

Use trigonometric ratios to find the unknown side lengths in the triangles below. Round your answers to the nearest hundredth.
::使用三角比来查找以下三角形中未知的侧边长度。将您的答案绕到最近的一百位。

For problems 11-13 use the given information about $\begin{aligned} Δ A B C \end{aligned}$ with right angle $\begin{aligned} B \end{aligned}$ to find the unknown side lengths. Round your answer to the nearest hundredth.
::对于问题 11-13 , 使用带有右角 B 的 QABC 信息来查找未知的侧边长度。将您的答复四舍五入到最近的一百。

$\begin{aligned} a = 12 \end{aligned}$ and $\begin{aligned} m ∠ A = 43^{\circ} \end{aligned}$
::a=12和mA=43

$\begin{aligned} m ∠ C = 75^{\circ} \end{aligned}$ and $\begin{aligned} b = 24 \end{aligned}$
::mC=75和b=24

$\begin{aligned} c = 7 \end{aligned}$ and $\begin{aligned} m ∠ A = 65^{\circ} \end{aligned}$
::c=7和mA=65

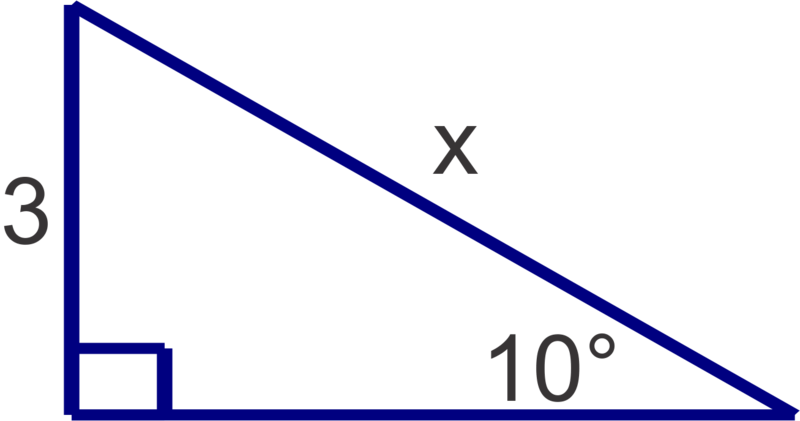
A ramp needs to have an angle of elevation no greater than 10 degrees. If the door is 3 ft above the sidewalk level, what is the minimum possible ramp length to the nearest tenth of a foot?
::斜坡需要有一个高度角不大于10度。如果门高于人行道水平3英尺,那么最接近10英尺的坡道长度是多少?

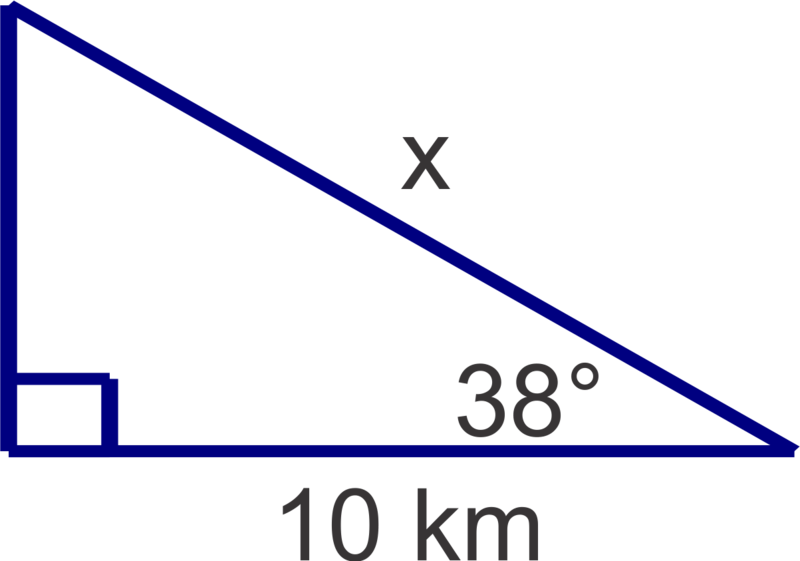
A ship, Sea Dancer , is 10 km due East of a lighthouse. A second ship, Nelly , is due north of the lighthouse. A spotter on the Sea Dancer measures the angle between the Nelly and the lighthouse to be $\begin{aligned} 38^{\circ} \end{aligned}$ . How far apart are the two ships to the nearest tenth of a kilometer?
::另一艘船,内利,在灯塔以北。海上舞蹈家的探察器将内利和灯塔之间的角测量为38英寸。两艘船距离距离最近的十分之一公里有多远?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

顺弦、顺弦、正弦

Sine, Cosine and Tangent ::顺弦、顺弦和唐敏

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Sine, Cosine and Tangent
::顺弦、顺弦和唐敏

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)