Course: 5.2 两维职位和中点

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 两维中的位置和中点

Collapse Expand
两维中的位置和中点
A digital graphic artist is designing a new company logo. Currently she is sketching a sample on graph paper to show her client, and needs to find the center of the text she has drawn so she can line up the artwork properly.
::一位数字图形艺术家正在设计一个新的公司标志。目前,她正在绘制图表纸上的样本,以展示客户,她需要找到她所绘制的文字的中心,以便她能够正确排列艺术作品。

If she knows that the first letter starts 10 boxes up and 5 boxes over from the bottom-left corner of the page, and the last letter ends 12 boxes up and 32 boxes over from the same corner, how could she find the center?
::如果她知道第一个字母是从页面左下角开始的10个箱子和5个箱子, 最后一个字母从同一个角落结束的12个箱子和32个箱子, 她怎么能找到中间位置?

Positions and Midpoints in Two Dimensions
::两维中的位置和中点

Using the Coordinate System Efficiently
::高效使用坐标系统

In the past, as you used the coordinate system for graphing in algebra and geometry, you probably became very familiar with the x / y axes running left/right and up/down on the page, with 0 in the center. In more advanced mathematics, and in physics or other motion studies, you will find that it is often much simpler to instead move the graph to line up with one vector than to align all of the vectors you are calculating with the standard orientation.
::过去,当你使用坐标系统用代数和几何来绘制图时,你可能非常熟悉在页面上左/右和上/下运行的x/y轴,中间有0轴。在更先进的数学、物理学或其他运动研究中,你会发现,将图与一个矢量排列起来比将计算的所有矢量与标准方向对齐要简单得多。

By aligning one of multiple vectors with either the x or y axis, and/or setting the origin of your graph at the start of a vector, you minimize the complexity of your calculations.
::通过将多个矢量之一与 x 或 Y 轴对齐,以及/或者在矢量起始处设置图形来源,您将计算的复杂性最小化。

Vectors Between Two Points
::两个点之间的矢量

A d isplacement vector represents motion beginning at one point and ending at another. In the diagram below, vector C starts at point A and ends at point B. This means that $\begin{aligned} \vec{A} + \vec{C} = \vec{B} \end{aligned}$ and $\begin{aligned} \vec{C} = \vec{B} - \vec{A} \end{aligned}$ . In this case, $\begin{aligned} \vec{A} = ⟨ 1, 3 ⟩ \end{aligned}$ and $\begin{aligned} \vec{B} = ⟨ 3, 2 ⟩ \end{aligned}$ , therefore $\begin{aligned} \vec{C} = ⟨ (3 - 1), (2 - 3) ⟩ = ⟨ 2, - 1 ⟩ \end{aligned}$ matching what we can see in the diagram.
::迁移矢量代表从一个点开始、到另一个点结束的运动。在下图中,矢量C从A点开始,到B点结束。这意味着 ACBBBBBBBABBBBBBBBBBABBBC1和B3,2B3,2C(3-1)CC3⁄3⁄2⁄1C匹配图表中我们可以看到的。

Vector to a Point Between Two Points
::矢量到两点之间两点之间的一点

Computer graphics artists frequently need to know the location of a point which lies midway between two other points. Once we know the position vectors for two discrete points, we can determine the midpoint between them using their coordinates. Specifically, the midpoint between points A and B is the “average” of the two positions, therefore the coordinates of the midpoint are given by $\begin{aligned} x_{m p} = \frac{1}{2} (x_{A} + x_{B}), y_{m p} = \frac{1}{2} (y_{A} + y_{B}) \end{aligned}$ , and $\begin{aligned} z_{m p} = \frac{1}{2} (z_{A} + z_{B}) \end{aligned}$ and the position vector for the midpoint can be written as $\begin{aligned} P_{m p} = ⟨ x_{m p}, y_{m p}, z_{m p} ⟩ \end{aligned}$ . The vector from any other point to this midpoint can then be calculated using the method described in our discussion of displacement vectors.
::计算机图形艺术家经常需要知道位于另外两个点中间的一个点的位置。一旦我们知道两个离散点的位置矢量, 我们就可以使用它们的坐标来确定它们之间的中点。具体地说, A点和 B点之间的中点是这两个位置的“ 平均 ” , 因此中点的坐标由 xmp=12( xA+xB)、 ymp=12(yA+yB) 和 zmp=12(zA+zB) 给出, 中点的中点的向量可以写成 Pmpxmp,ymp,zmp 。从任何其他点到这个中点的矢量可以使用我们在讨论移位矢量时描述的方法计算。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about finding the center of text on a sheet of graph paper.
::早些时候,有人给了你一个问题在图纸页上找到文字的中心

If she knows that the first letter starts 10 boxes up and 5 boxes over from the bottom-left corner of the page, and the last letter ends 12 boxes up and 32 boxes over from the same corner, how could she find the center?
::如果她知道第一个字母是从页面左下角开始的10个箱子和5个箱子, 最后一个字母从同一个角落结束的12个箱子和32个箱子, 她怎么能找到中间位置?

This is a midpoint question, so the x coordinate calculation is: $\begin{aligned} x_{m p} = \frac{1}{2} (x_{A} + x_{B}) = \frac{1}{2} (5 + 32) = 18.5 \end{aligned}$
::这是一个中点问题, 所以x坐标计算是: xmp=12( xA+xB)=12( 5+32)=18.5。

and the y-coordinate of the midpoint is given by: $\begin{aligned} y_{m p} = \frac{1}{2} (y_{A} + y_{B}) = \frac{1}{2} (10 + 12) = 11 \end{aligned}$
::中点的 Y 坐标由 : ymp= 12(yA+yB)= 12( 10+12)= 11 给出。

The coordinate of the center is: $\begin{aligned} 18.5, 11 \end{aligned}$ .
::中心坐标是18.511

Example 2
::例2

The motion of an object along an inclined plane is a very common problem in introductory physics. The diagram below shows one such situation.
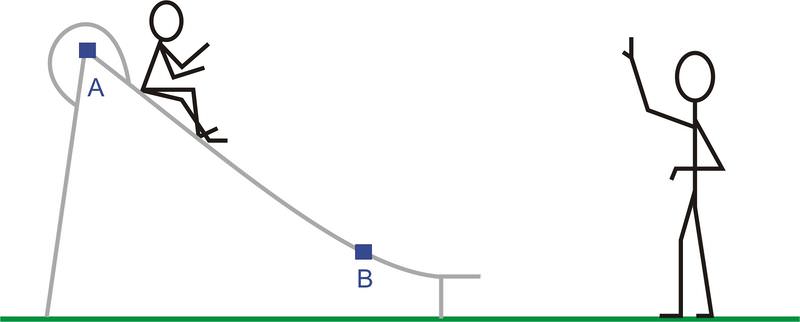
::物体沿着倾斜平面运动是入门物理学中一个非常常见的问题。

Stickman Beauford has taken his niece Brynna to the park and waves to her as she plays on the slide. Choose two coordinate systems that could be used to describe Brynna’s motion and identify the position vectors for points A and B in both coordinate systems.
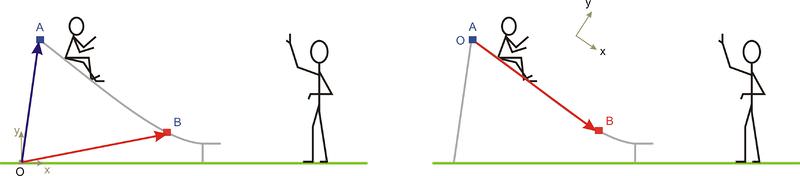
::施特曼·博福德(Sickman Beauford)带他的侄女布伦纳去公园,并在她玩滑板时向她挥手。选择两个可用来描述布莱纳运动的坐标系统,并确定两个坐标系统中A点和B点的位置矢量。

If we want to describe Brynna’s motion as she moves from point A to point B along the slide, we could use a standard horizontal and vertical coordinate system with the origin at the base of the slide’s ladder, but then the vector describing her motion would have components in both the x and y directions. Our mathematical description of her motion can be greatly simplified if we choose point A to be the origin and if we rotate the coordinate system such that the x-axis is parallel to the slide and the y-axis is perpendicular to the slide. Now Brynna’s motion from point A to point B is only along the x-axis. Note, other choices of origin are possible.
::如果我们想描述Brynna在幻灯片上从A点向B点移动时的动作,我们就可以使用标准水平和垂直协调系统,其来源在幻灯片的梯子底部,但描述其动作的矢量将具有x和y方向的成分。如果我们选择A点作为源头,如果我们旋转坐标系统,使x轴与幻灯片平行,Y轴与幻灯片垂直。现在,Brynna从A点到B点的动作只能沿着X轴线进行。注意,其他来源的选择是可能的。

Once we have identified an origin and coordinate axes for of our reference frames, we can use vector notation to identify the location of points A and B. The position vector for point A is the vector starting at the origin and ending at point A, $\begin{aligned} \vec{O A} \end{aligned}$ . For the standard coordinate system shown on the left above, the position vectors $\begin{aligned} \vec{O A} \end{aligned}$ and $\begin{aligned} \vec{O B} \end{aligned}$ are shown on the left below. For the rotated coordinate system, shown on the right above, the position vector $\begin{aligned} \vec{O A} = 0 \end{aligned}$ and $\begin{aligned} \vec{O B} = \vec{A B} \end{aligned}$ .
::一旦我们为我们的参照框架确定了来源并协调了轴轴,我们就可以使用矢量标记来确定A点和B点的位置。A点的位置矢量是指从源点A开始到A点OAQQ的矢量。对于上述左侧显示的标准协调系统,OAQQ和OBQN的位置在下面左侧显示。对于以上右侧显示的旋转坐标系统,OAQQQO和OBQABQQ。

Example 3
::例3

Determine the coordinates and magnitude of the vector, D , beginning at the point $\begin{aligned} \vec{P_{1}} = ⟨ 12, 7 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 8, 10 ⟩ \end{aligned}$ .
::确定矢量(D)的坐标和大小,从P112、7点开始,至P28、10结束。

The displacement vector D is the difference between the two position vectors:.
::移位矢量 D 是两个位置矢量之间的差异 :

$\begin{aligned} D = ⟨ P_{2 x} - P_{1 x}, P_{2 y} - P_{1 y} ⟩ = ⟨ 8 - 12, 10 - 7 ⟩ = ⟨ - 4, 3 ⟩ \end{aligned}$ .
::DP2x-P1x,P2y-P18-12,10-74,3。

The magnitude of the vector, D , can be found using the Pythagorean theorem:
::矢量的大小, D, 可以用 Pythagorean 定理找到 :

$\begin{aligned} | \vec{D} | = \sqrt{(- 4)^{2} + (3)^{2}} = \sqrt{25} = 5 \end{aligned}$ .
::D(-4)2+(3)2=25=5。

Example 4
::例4

Determine the position vector identifying the midpoint between points $\begin{aligned} \vec{P_{1}} = ⟨ 12, 7 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 8, 10 ⟩ \end{aligned}$ .
::确定位置矢量,确定P112、7和P28、10之间的中点。

Since these two points are located in the x-y plane, the x-coordinate of the midpoint is given by
::由于这两个点位于X-y平面,中点的X坐标由下列人员提供:

$\begin{aligned} x_{m p} = \frac{1}{2} (x_{A} + x_{B}) = \frac{1}{2} (12 + 8) = 10 \end{aligned}$
::xmp=12( xA+xB)=12( 12+8)=10

and the y-coordinate of the midpoint is given by
::中点的 Y 坐标由

$\begin{aligned} y_{m p} = \frac{1}{2} (y_{A} + y_{B}) = \frac{1}{2} (7 + 10) = 8.5 \end{aligned}$ .
::ymp=12(yA+yB)=12(7+10)=8.5。

Therefore the position vector for this midpoint can be written as
::因此,此中点的位置矢量可以写为

$\begin{aligned} P_{m p} = ⟨ 10, 8.5 ⟩ \end{aligned}$
::Pmp 10, 8.5

Example 5
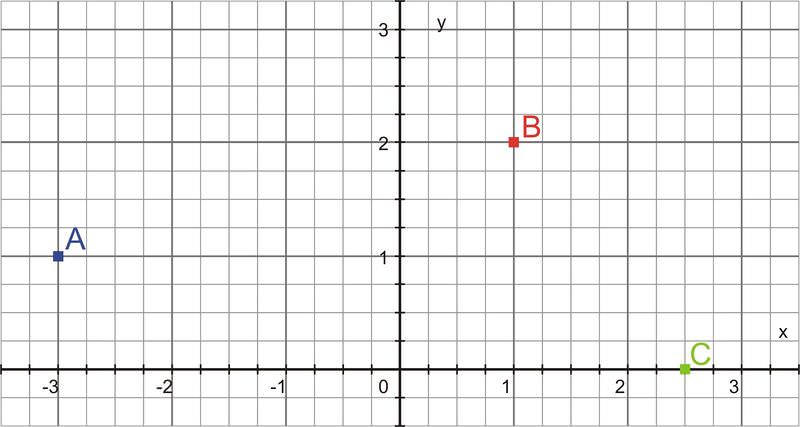
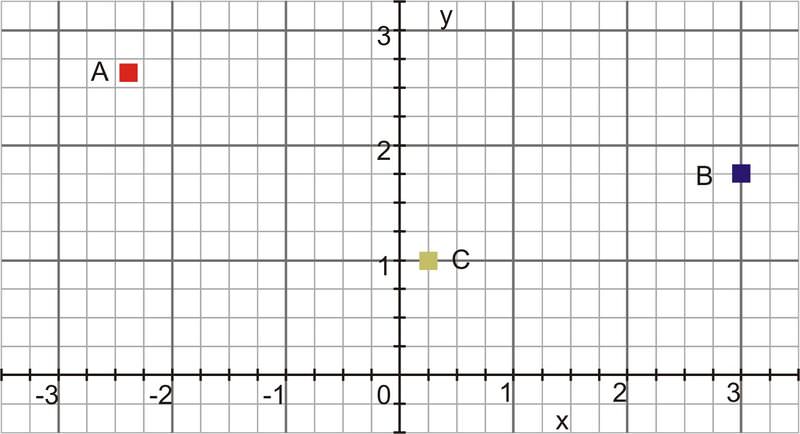
::例5

Identify the position vectors for the three points shown on the grid below.
::确定以下网格上显示的三个点的位置矢量。

The position vectors begin at the origin, (0, 0) and end at each point:
::位置矢量从来源于( 0, 0)开始,到每个点结束:

$\begin{aligned} \vec{O A} = ⟨ - 3, 1 ⟩, \vec{O B} = ⟨ 1, 2 ⟩ \end{aligned}$ and : $\begin{aligned} \vec{O C} = ⟨ 2.5, 0 ⟩ \end{aligned}$
::OA3,1,OB1,2 和:OC2.5,0

Example 6
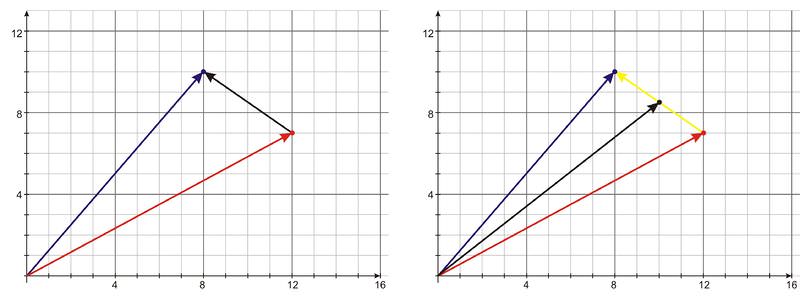
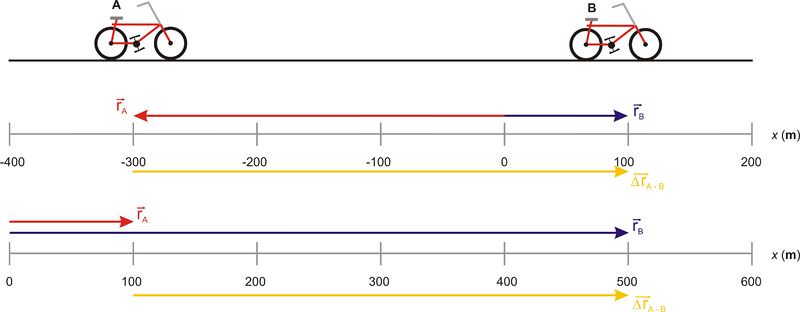
::例6

The diagram shows two positions of a bicycle as it moves along a long straight road. Two possible coordinate systems for the motion are shown below. Determine the position vectors in each of the two coordinate systems for the bicycle at points A and B. Then determine the displacement vector from A to B in each case. (Not drawn to scale.)
::图表显示自行车在一条长长的直路上行走时的两个位置。下面显示两种可能的动作协调系统。在A点和B点确定自行车两个坐标系统中的每一个位置矢量。然后在每种情况下确定从A到B的迁移矢量。 (未划为缩放范围。)

The diagram shows two positions of a bicycle as it moves along a long straight road. Two possible coordinate systems for the motion are shown below. Determine the position vectors in each of the two coordinate systems for the bicycle at points A and B. Then determine the displacement vector from A to B in each case.
::图表显示自行车在一条长长的直路上行走时的两个位置。下面显示两个可能的动作协调系统。确定A点和B点两个自行车协调系统中的每一个位置矢量。然后确定每个情况下从A到B的迁移矢量。

For the upper coordinate system, the position vector of the bicycle at point A is given by $\begin{aligned} \vec{r_{A}} = ⟨ - 300 m, 0, 0 ⟩ \end{aligned}$ and that at point B is given by $\begin{aligned} \vec{r_{B}} = ⟨ 100 m, 0, 0 ⟩ \end{aligned}$ . This gives a displacement of $\begin{aligned} \vec{△ r_{A - B}} = ⟨ (100 m - (- 300 m)), (0 - 0), (0 - 0) ⟩ = ⟨ 400 m, 0, 0 ⟩ . \end{aligned}$
::对于上坐标系统,A点的自行车位置矢量由 rA-300m,0,0 给出,B点由 rB-100m,0,0 给出。这就使 rA-B (100m-(300m)),(0-0),(0-0) 400m,0,0的位移。

For the upper coordinate system, the position vector of the bicycle at point A is given by $\begin{aligned} \vec{r_{A}} = ⟨ 100 m, 0, 0 ⟩ \end{aligned}$ and that at point B is given by $\begin{aligned} \vec{r_{B}} = ⟨ 500 m, 0, 0 ⟩ \end{aligned}$ . This gives a displacement of $\begin{aligned} \vec{△ r_{A - B}} = ⟨ (500 m - 100 m), (0 - 0), (0 - 0) ⟩ = ⟨ 400 m, 0, 0 ⟩ . \end{aligned}$
::就上坐标系统而言,A点的自行车位置矢量由 rA 100m,0,0 给出,B点由 rB 500m,0,0 给出,这导致 rA-B (500m-100m),(0-0),(0-0) 400m,0,0的位移。

The position vectors for the bicycle at point A are shown in red and the position vectors for point B are shown in blue. The displacement vector between points A and B is shown in gold. As you can see, the position vectors representing this motion depend on the choice of coordinate system, but the displacement vector is independent of the coordinate system. No matter how we define the origin, the bike moves 400 m in the + x direction and does not move in the y or z direction.
::A点的自行车位置矢量以红色显示, B点的位置矢量以蓝色显示。 A点和 B点之间的移位矢量以金色显示。您可以看到,代表此运动的定位矢量取决于协调系统的选择,但移位矢量独立于协调系统。无论我们如何定义来源,自行车在 +x 方向移动400米,而不会在 y 或 z 方向移动。

Example 7
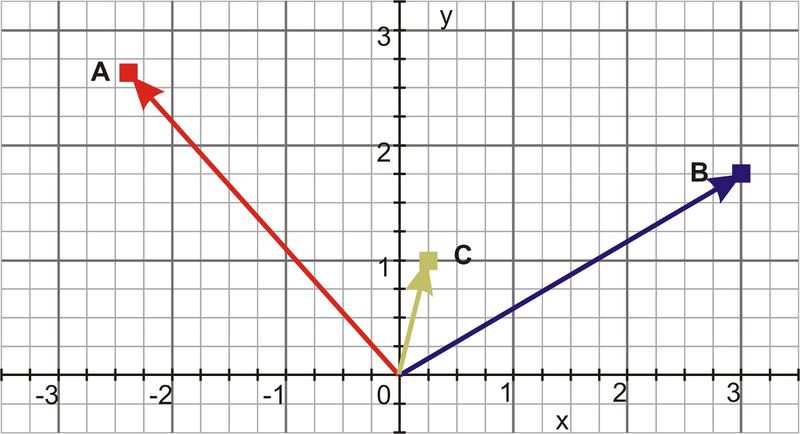
::例7

Identify the position vectors for the three points shown in the diagram below.
::确定下图所示三点的位置矢量。

$\begin{aligned} \vec{r_{A}} = ⟨ - 2.63, 2.63, 0 ⟩, \vec{r_{B}} = ⟨ 3, 1.75, 0 ⟩, \vec{r_{C}} = ⟨ 0.25, 1, 0 ⟩ \end{aligned}$
::rA2.63,2.63,0,rB3,1.75,0,rC0.25,1,0

Review
::回顾

What is a displacement vector used for?
::用于什么迁移矢量的迁移矢量?

Determine the coordinates and magnitude of the displacement vector, D, beginning at the point $\begin{aligned} \vec{P_{1}} \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} \end{aligned}$ .
::确定移位矢量(D)的坐标和大小,从P1 点开始,到P2 点结束。

$\begin{aligned} \vec{P_{1}} = ⟨ 25, 3 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 8, 11 ⟩ \end{aligned}$
::P125,33 至P28,1111

$\begin{aligned} \vec{P_{1}} = ⟨ 5, 3 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 7, 9 ⟩ \end{aligned}$
::P1,5,3 至P2,7,9

$\begin{aligned} \vec{P_{1}} = ⟨ 21, 18 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 4, 15 ⟩ \end{aligned}$
::P1,21,18,到P2,4,15

$\begin{aligned} \vec{P_{1}} = ⟨ 8, 5 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 5, 8 ⟩ \end{aligned}$
::P1,8,5 至P2,5,8

$\begin{aligned} \vec{P_{1}} = ⟨ 16, 25 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 9, 11 ⟩ \end{aligned}$
::P1 16,25 至P2,9,11

$\begin{aligned} \vec{P_{1}} = ⟨ 14, 3 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 23, 20 ⟩ \end{aligned}$
::P1 14,3 3 至P2 23,20

$\begin{aligned} \vec{P_{1}} = ⟨ 11, 4 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 15, 11 ⟩ \end{aligned}$
::P111,4 至P215,11

$\begin{aligned} \vec{P_{1}} = ⟨ 23, 13 ⟩ \end{aligned}$ and ending at $\begin{aligned} \vec{P_{2}} = ⟨ 1, 17 ⟩ \end{aligned}$
::P123,1313 至P21,17

Determine the position vector identifying the midpoint between points $\begin{aligned} \vec{P_{1}} \end{aligned}$ and $\begin{aligned} \vec{P_{2}} \end{aligned}$ .
::确定点P1和点P2之间的中点之间的位置矢量。

$\begin{aligned} \vec{P_{1}} = ⟨ 17, 6 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 18, 12 ⟩ \end{aligned}$
::P1 17,6 和P2 18,12

$\begin{aligned} \vec{P_{1}} = ⟨ 2, 5 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 1, 9 ⟩ \end{aligned}$
::P1,2,5和P2,1,9

$\begin{aligned} \vec{P_{1}} = ⟨ 24, 7 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 21, 10 ⟩ \end{aligned}$
::P1,24,7 和P2,21,10

$\begin{aligned} \vec{P_{1}} = ⟨ 12, 9 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 2, 20 ⟩ \end{aligned}$
::P112,9和P22,20

$\begin{aligned} \vec{P_{1}} = ⟨ 15, 17 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 18, 1 ⟩ \end{aligned}$
::P1 15,17 和P2 18,1

$\begin{aligned} \vec{P_{1}} = ⟨ 22, 14 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 23, 8 ⟩ \end{aligned}$
::P122,14和P223,8

$\begin{aligned} \vec{P_{1}} = ⟨ 1, 7 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 14, 21 ⟩ \end{aligned}$
::P1,1,7和P2,14,21

$\begin{aligned} \vec{P_{1}} = ⟨ 3, 9 ⟩ \end{aligned}$ and $\begin{aligned} \vec{P_{2}} = ⟨ 8, 1 ⟩ \end{aligned}$
::P1,3,9和P2,8,1

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

两维中的位置和中点

Positions and Midpoints in Two Dimensions ::两维中的位置和中点

Using the Coordinate System Efficiently ::高效使用坐标系统

Vectors Between Two Points ::两个点之间的矢量

Vector to a Point Between Two Points ::矢量到两点之间两点之间的一点

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)

Positions and Midpoints in Two Dimensions
::两维中的位置和中点

Using the Coordinate System Efficiently
::高效使用坐标系统

Vectors Between Two Points
::两个点之间的矢量

Vector to a Point Between Two Points
::矢量到两点之间两点之间的一点

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Review
::回顾

Review (Answers)
::回顾(答复)