Course: 13.3 逆三角函数和右三角的溶解

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 逆三角函数和正解右三角形

Collapse Expand
逆三角函数和正解右三角形
A right triangle has legs that measure 2 units and $\begin{aligned} 2 \sqrt{3} \end{aligned}$ units. What are the measures of the triangle's acute angles?
::右三角形的腿能测量2个单位和23个单位。三角形的急性角的度量是多少?

Inverse of Trigonometric Functions
::三角函数的逆函数

W e have used the trigonometric functions sine, cosine and tangent to find the ratio of particular sides in a right triangle given an angle. In this concept we will use the inverses of these functions, $\begin{aligned} \sin^{- 1} \end{aligned}$ , $\begin{aligned} \cos^{- 1} \end{aligned}$ and $\begin{aligned} \tan^{- 1} \end{aligned}$ , to find the angle measure when the ratio of the side lengths is known. When we type $\begin{aligned} \sin 30^{\circ} \end{aligned}$ into our calculator, the calculator goes to a table and finds the trig ratio associated with $\begin{aligned} 30^{\circ} \end{aligned}$ , which is $\begin{aligned} \frac{1}{2} \end{aligned}$ . When we use an inverse function we tell the calculator to look up the ratio and give us the angle measure. For example: $\begin{aligned} \sin^{- 1} (\frac{1}{2}) = 30^{\circ} \end{aligned}$ . On your calculator you would press $\begin{aligned} 2^{N D} SIN \end{aligned}$ to get $\begin{aligned} {SIN}^{- 1} ( \end{aligned}$ and then type in $\begin{aligned} \frac{1}{2} \end{aligned}$ , close the parenthesis and press ENTER. Your calculator screen should read $\begin{aligned} {SIN}^{- 1} (\frac{1}{2}) \end{aligned}$ when you press ENTER.
::我们使用三角函数正弦、正弦和正弦来查找右三角形中特定边边的比例。在这个概念中, 我们将使用这些函数的反函数, sin-1、 cos-1 和 tan-1, 以找到边长比的角度量。当我们在计算器中输入 sin\\ 30 时, 计算器会进入一个表格, 并找到与 30 相关的三角比, 也就是 12 。当我们使用反函数时, 我们告诉计算器来查看这个比例, 并给出角度量。例如 : sin- 1 {( 12) =30 。在您的计算器上, 您可以按 2NDSIN 键以获得 SIN-1 ( 并在 12 键上输入), 关闭括号并按 ENTER 键。您按 ENTER 时, 您的计算器屏幕应该读 SIN-1( 12) 。

Let's find the measure of angle $\begin{aligned} A \end{aligned}$ associated with the following ratios and round answers to the nearest degree .
::让我们找到角度A的量度与以下比率和圆形答案相关到最接近的程度。

$\begin{aligned} \sin A = 0.8336 \end{aligned}$
::A=0.8336

$\begin{aligned} \tan A = 1.3527 \end{aligned}$
::泰纳=1.3527

$\begin{aligned} \cos A = 0.2785 \end{aligned}$
::COS=0.2785 COS=0.2785

Using the calculator we get the following:
::使用计算器,我们得到以下数据:

$\begin{aligned} \sin^{- 1} (0.8336) \approx 56^{\circ} \end{aligned}$
:0.8336) 56

$\begin{aligned} \tan^{- 1} (1.3527) \approx 54^{\circ} \end{aligned}$
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

$\begin{aligned} \cos^{- 1} (0.2785) \approx 74^{\circ} \end{aligned}$
:0.2785)74

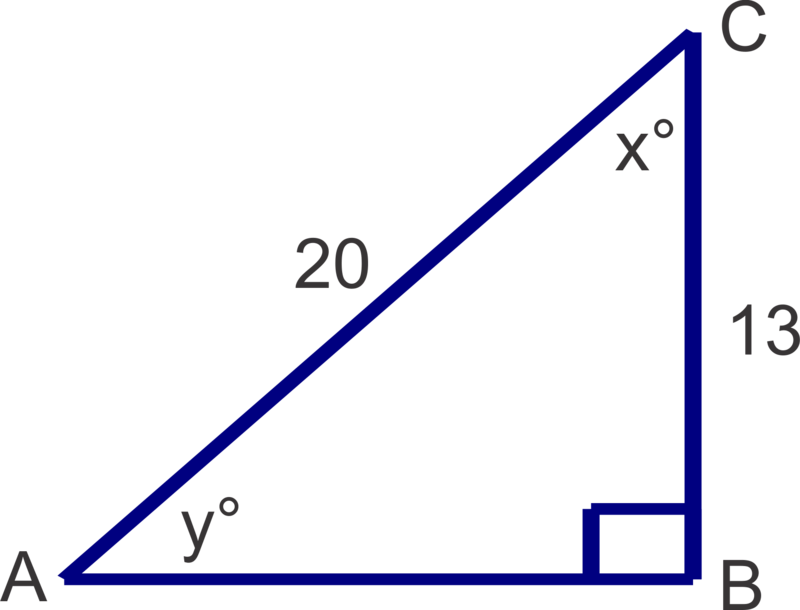
Now, let's find the measures of the unknown angles in the triangle shown and round answers to the nearest degree.
::现在,让我们来看看三角形中未知角度的度量以及最接近的圆形答案

We can solve for either $\begin{aligned} x \end{aligned}$ or $\begin{aligned} y \end{aligned}$ first. If we choose to solve for $\begin{aligned} x \end{aligned}$ first, the 23 is opposite and 31 is adjacent so we will use the tangent ratio.
::我们可以先解决 x 或 y 先解决。如果我们选择先解决 x 先解决, 23 是相反的, 31 是相邻的, 所以我们将使用正切比。

$\begin{aligned} x = \tan^{- 1} (\frac{23}{31}) \approx 37^{\circ} . \end{aligned}$

::X=tan-1(2331)37。

Recall that in a right triangle, the acute angles are always complementary, so $\begin{aligned} 90^{\circ} - 37^{\circ} = 53^{\circ} \end{aligned}$ , so $\begin{aligned} y = 53^{\circ} \end{aligned}$ . We can also use the side lengths an a trig ratio to solve for $\begin{aligned} y \end{aligned}$ :
::回顾在右三角形中, 急性角度总是互补的, 所以 903753, 所以y=53。我们也可以使用侧边长度一个三重比来解答 y:

$\begin{aligned} y = \tan^{- 1} (\frac{31}{23}) \approx 53^{\circ} . \end{aligned}$

::y'tan -1(3123) 53。

Finally, let's solve the right triangle shown below and round all answers to the nearest tenth.
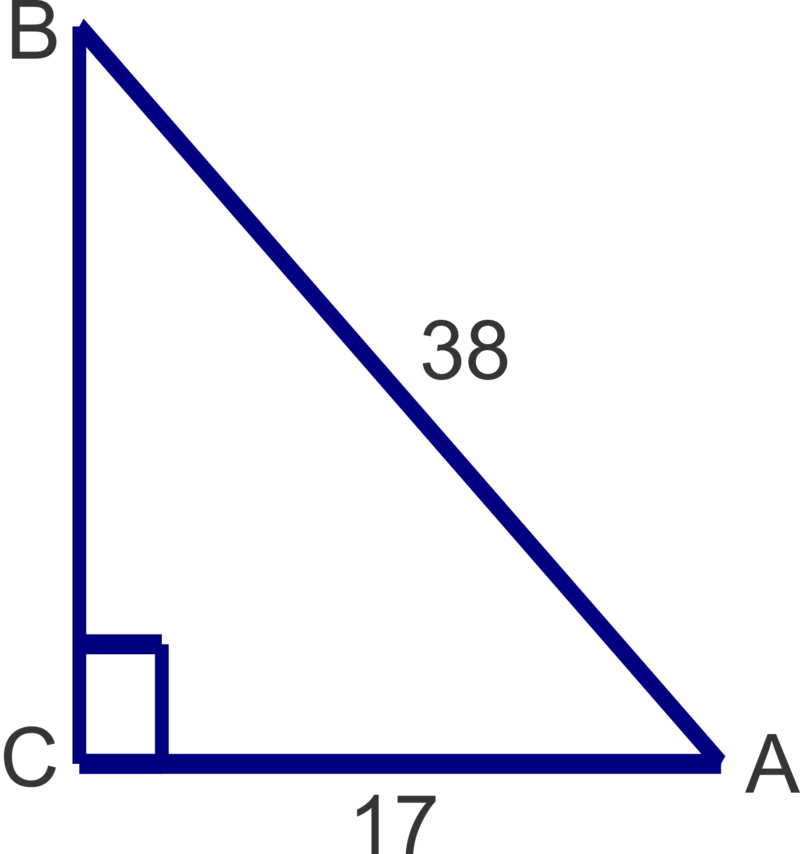
::最后,让我们解开下面显示的右三角形, 将所有答案转到最近的第十个答案。

We can solve for either angle $\begin{aligned} A \end{aligned}$ or angle $\begin{aligned} B \end{aligned}$ first. If we choose to solve for angle $\begin{aligned} B \end{aligned}$ first, then 8 is the hypotenuse and 5 is the opposite side length so we will use the sine ratio.
::我们可以首先解决角度 A 或角度 B 。如果我们选择先解决角度 B , 那么8 是下限, 5 是反侧长度, 所以我们将使用正弦比例。

$\begin{aligned} \sin B & = \frac{5}{8} \\ m ∠ B & = \sin^{- 1} (\frac{5}{8}) \approx {38.7}^{\circ} \end{aligned}$

::B=58m_B=sin_1}(58)_38.7

Now we can find $\begin{aligned} A \end{aligned}$ two different ways.
::现在我们可以找到两种不同的方式。

Method 1: We can using trigonometry and the cosine ratio:
$\begin{aligned} \cos A & = \frac{5}{8} \\ m ∠ A & = \cos^{- 1} (\frac{5}{8}) \approx {51.3}^{\circ} \end{aligned}$

::方法1:我们可以使用三角测量法和余弦比:cosA=58mA=cos-1(58)51.3

Method 2: We can subtract $\begin{aligned} m ∠ B \end{aligned}$ from $\begin{aligned} 90^{\circ} \end{aligned}$ : $\begin{aligned} 90^{\circ} - {38.7}^{\circ} = {51.3}^{\circ} \end{aligned}$ since the acute angles in a right triangle are always complimentary.
::方法2:我们可以从 90\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Either method is valid, but be careful with Method 2 because a miscalculation of angle $\begin{aligned} B \end{aligned}$ would make the measure you get for angle $\begin{aligned} A \end{aligned}$ incorrect as well.
::这两种方法都有效,但对于方法2要小心,因为对角度B的误算会使对角度A的测量也错误。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the measures of the triangle's acute angles.
::早些时候,有人要求你找到三角形的急性角度的测量结果

First, let's find the hypotenuse, then we can solve for either angle.
::首先,让我们找到低温, 然后我们可以解决两个角度。

$\begin{aligned} 2^{2} + (2 \sqrt{3})^{=} c^{2} \\ 4 + 12 = c^{2} \\ 16 = c^{2} \\ c = 4 \end{aligned}$

::22+(23)=c24+12=c216=c2c=4

One of the acute angles will have a sine of $\begin{aligned} \frac{2}{4} = \frac{1}{2} \end{aligned}$ .
::一个急性角度的正弦值为 24=12。

$\begin{aligned} \sin A & = \frac{1}{2} \\ m ∠ A & = \sin^{- 1} \frac{1}{2} = 30^{\circ} \end{aligned}$

::A=12m_A=sin_1_12=30_BAR__BAR_A=sin_1_12=30_BAR_A=sin_1_A=sin_12=30_BAR_

Now we can find $\begin{aligned} B \end{aligned}$ by subtracting $\begin{aligned} m ∠ A \end{aligned}$ from $\begin{aligned} 90^{\circ} \end{aligned}$ : $\begin{aligned} 90^{\circ} - 30^{\circ} = 60^{\circ} \end{aligned}$ since the acute angles in a right triangle are always complimentary.
::现在我们可以通过从 90 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

Example 2
::例2

Find the measure of angle $\begin{aligned} A \end{aligned}$ .
::查找角度A的量度。

$\begin{aligned} \sin A = 0.2894 \end{aligned}$
::A=0.2894

$\begin{aligned} \sin^{- 1} (0.2894) \approx 17^{\circ} \end{aligned}$
::-1 (0.2894) 17

Example 3
::例3

Find the measure of angle $\begin{aligned} A \end{aligned}$ .
::查找角度A的量度。

$\begin{aligned} \tan A = 2.1432 \end{aligned}$
::A=2.1432

$\begin{aligned} \tan^{- 1} (2.1432) \approx 65^{\circ} \end{aligned}$
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

Example 4
::例4

Find the measure of angle $\begin{aligned} A \end{aligned}$ .
::查找角度A的量度。

$\begin{aligned} \cos A = 0.8911 \end{aligned}$
::A=0.8911 COS=0.8911

$\begin{aligned} \cos^{- 1} (0.8911) \approx 27^{\circ} \end{aligned}$
::================================================================================================================================== ================================================================================================================================================================================================================================

Example 5
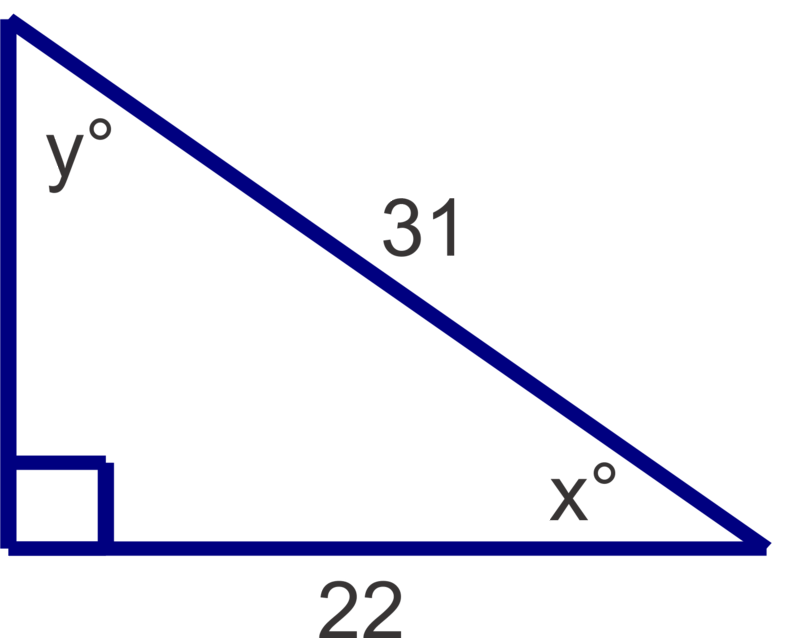
::例5

Find the measures of the unknown angles in the triangle shown. Round answers to the nearest degree.
::查找所显示三角形中未知角度的度量。圆圆回答到最接近的度。

$\begin{aligned} x = \cos^{- 1} (\frac{13}{20}) \approx 49^{\circ}; y = \sin^{- 1} (\frac{13}{20}) \approx 41^{\circ} \end{aligned}$

::x=cos- 1( 1320) 49;y=sin- 1( 1320) 41

Example 6
::例6

Solve the triangle. Round side lengths to the nearest tenth and angles to the nearest degree.
::解开三角形。圆边长至最近的十分点, 角度到最近的高度。

$\begin{aligned} m ∠ A = \cos^{- 1} (\frac{17}{38}) \approx 63^{\circ}; m ∠ B = \sin^{- 1} (\frac{17}{38}) \approx 27^{\circ}; a = \sqrt{38^{2} - 17^{2}} \approx 34.0 \end{aligned}$

::mA=cos-1(1738)__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Review
::回顾

Use your calculator to find the measure of angle $\begin{aligned} B \end{aligned}$ . Round answers to the nearest degree.
::使用您的计算器找到角度 B. 圆圆答案的量值, 以至最近的度。

$\begin{aligned} \tan B = 0.9523 \end{aligned}$
::泰纳B=0.9523

$\begin{aligned} \sin B = 0.8659 \end{aligned}$
::B=0.8659

$\begin{aligned} \cos B = 0.1568 \end{aligned}$
::COS=0.1568 COS=0.1568

$\begin{aligned} \sin B = 0.2234 \end{aligned}$
::B=0.2234

$\begin{aligned} \cos B = 0.4855 \end{aligned}$
::COS=0.4855 COS=0.4855 COS=0.4855

$\begin{aligned} \tan B = 0.3649 \end{aligned}$
::tan_B=0.3649

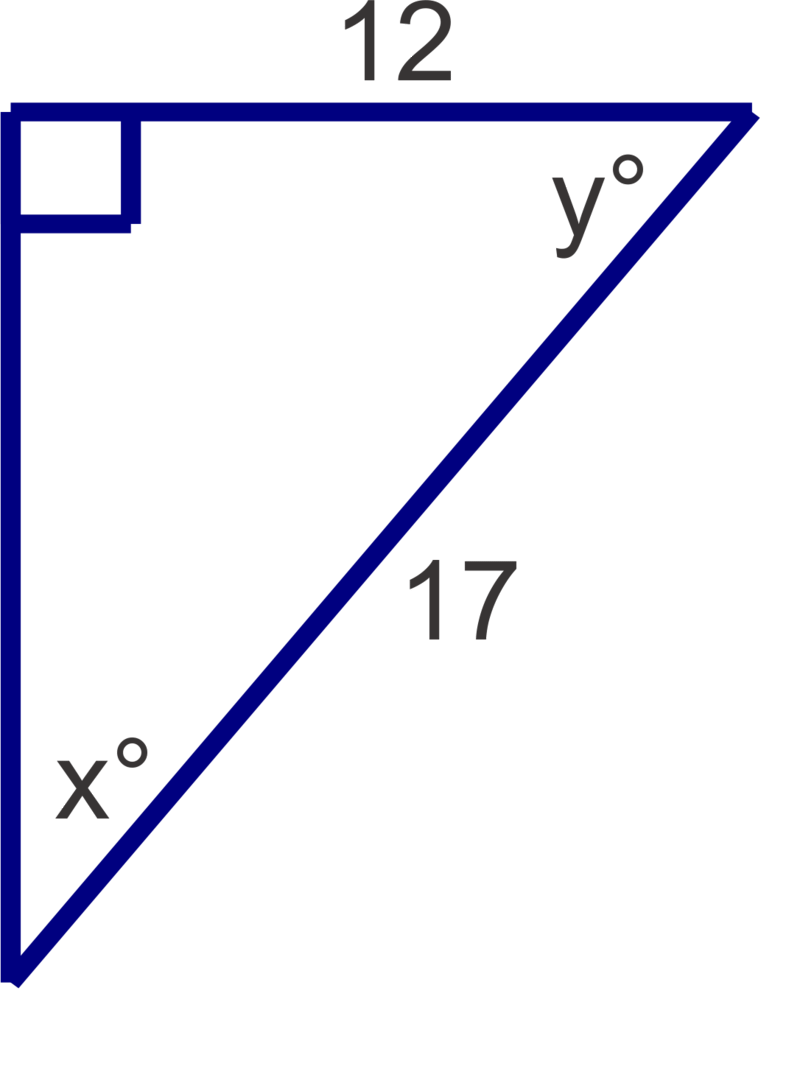
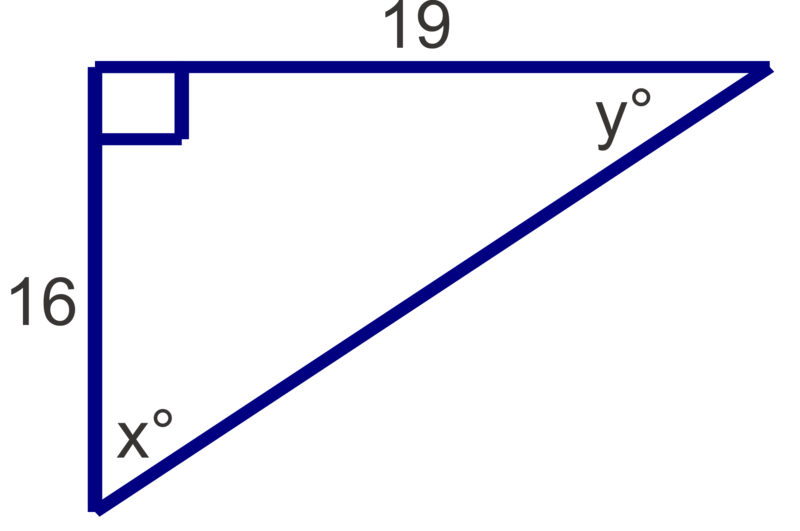
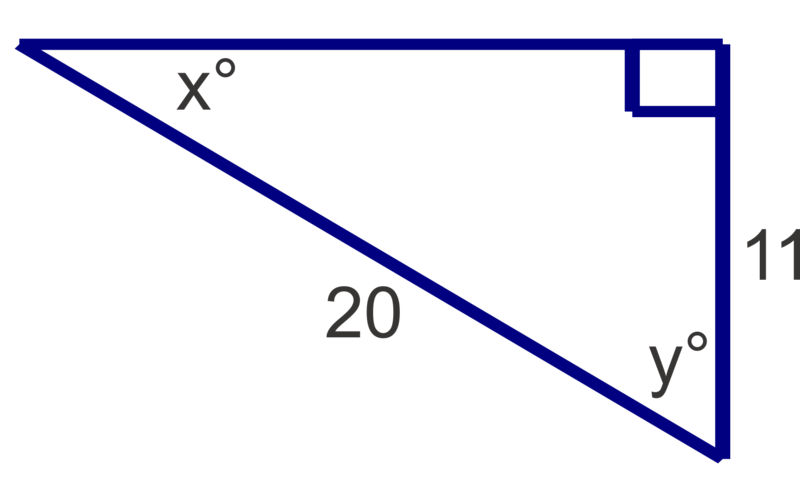
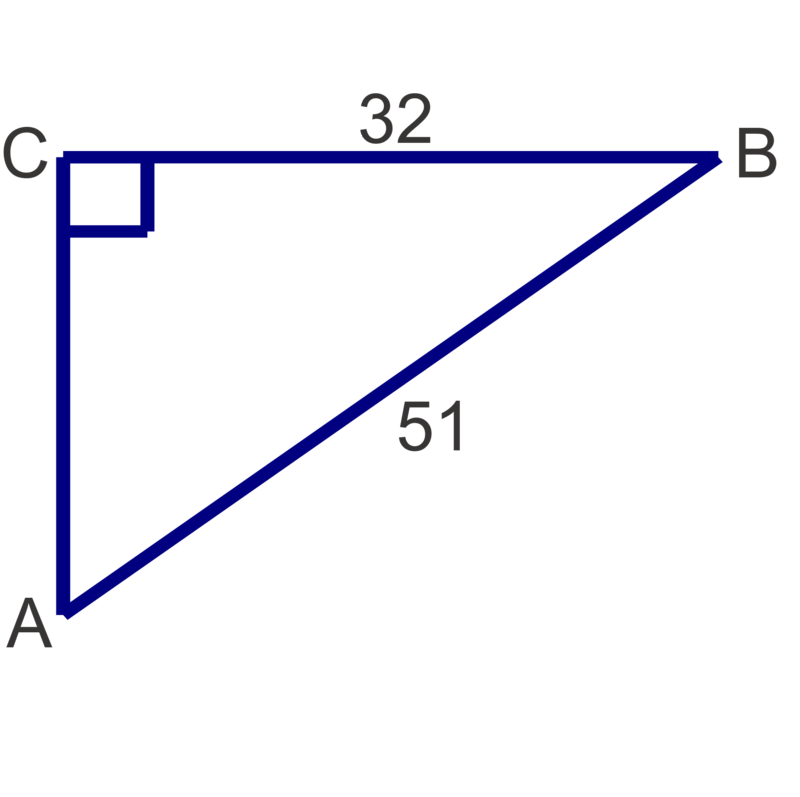
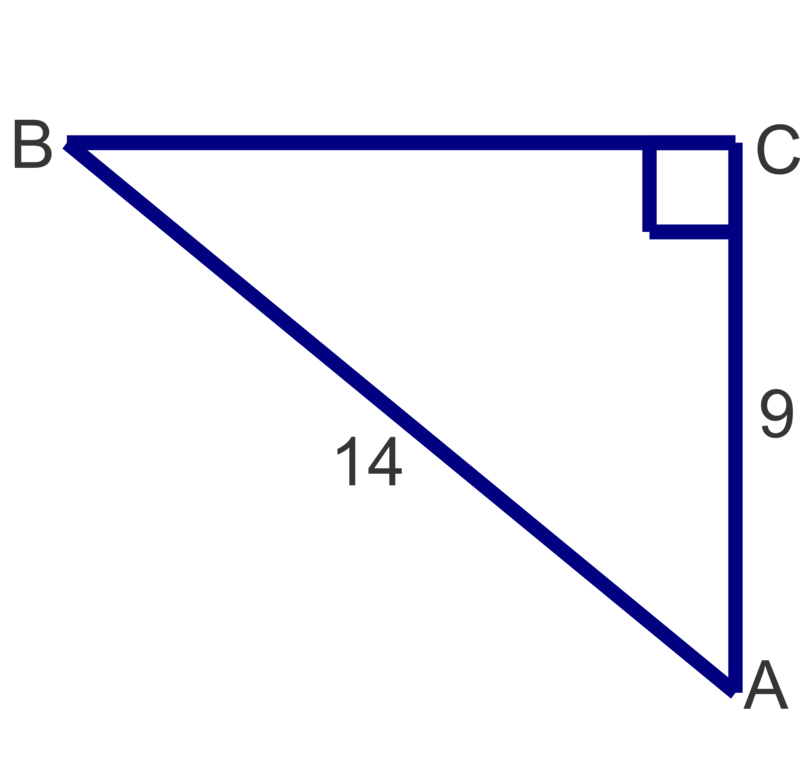
Find the measures of the unknown acute angles. Round measures to the nearest degree.
::查找未知急性角度的测量。圆形测量到最接近的程度。

Solve the following right triangles. Round angle measures to the nearest degree and side lengths to the nearest tenth.
::解决以下右三角形。圆角测量到最接近的位数和最接近的十分位数的侧边长度。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

逆三角函数和正解右三角形

Inverse of Trigonometric Functions ::三角函数的逆函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Inverse of Trigonometric Functions
::三角函数的逆函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)