5.4 点5.4产品

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 点产品

  Collapse Expand

  点产品

  播放段落

  Kelly is learning about flying airplanes so she can apply to take her pilot's exam. Right now she is studying the effect of wind on a flying plane, and she is supposed to describe the added "push" effect a NE wind of 50 mph would have on a plane traveling at 30 mph due NE relative the ground.
  ::Kelly正在学习飞行飞机,以便申请参加驾驶员考试。现在,她正在研究风对飞行飞机的影响,她应该描述在飞行飞机上增加的“推”效应,即NE风50毫米,在飞行30米的飞机上,NE与地面相对。

  播放段落

  How can she describe the combination of forces in the NE direction?
  ::她如何描述NE方向的力量组合?

  播放段落

  Dot Products
  ::点产品

  播放段落

  In common terms, the dot product of two vectors is a number that describes the amount of force that two different vectors both contribute in the direction. This value results from the multiplication of the appropriate parts of each vector, and is therefore sometimes referred to as the scalar product of the two vectors.
  ::通常,两个矢量的点产物是一个数字,它说明两种不同的矢量都朝向贡献的强度,这一数值来自每种矢量的适当部分的倍增,因此有时被称为两个矢量的标量产物。

  播放段落

  A dot product is a scalar quantity which varies as the angle between the two vectors changes. The angle between the vectors affects the dot product because the portion of the total force of a vector dedicated to a particular direction goes up or down if the entire vector is pointed toward or away from that direction.
  ::圆点产品是一个数量级数,随两个矢量之间的角变化而变化。矢量之间的角影响点产品,因为矢量用于特定方向的总力部分会上下移动,如果矢量被指向或偏离该方向,则整个矢量的全部力量部分会向上或向下移动。

  播放段落

  The maximum value for the dot product occurs when the two vectors are parallel to one another (all 'force' from both vectors is in the same direction), but when the two vectors are perpendicular to one another, the value of the dot product is equal to 0 (one vector has zero force aligned in the direction of the other, and any value multiplied by zero is zero).
  ::当两个矢量平行(两个矢量的所有“力”都朝同一方向),但当两个矢量相互垂直时,点产值等于0(一个矢量在另一个方向上为零,任何值乘以零为零)时,点产值即为0(一个矢量在另一个方向上为零,任何值乘以零为零)。

  播放段落

  There are two ways to calculate the dot product. One way is to multiply the individual components. Each component of vector $\begin{array}{r}\stackrel{\to }{A}\end{array}$ is multiplied by the component of vector $\begin{array}{r}\stackrel{\to }{B}\end{array}$ which is in the same direction. Then we add the results.
  ::计算点产品有两种方法。 一种是乘以单个组件。 矢量 A 的每个组件乘以方向相同的矢量 B 的组件。 然后我们添加结果 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=A_x{B}_x+A_y{B}_y+A_z{B}_z+...\end{array}$
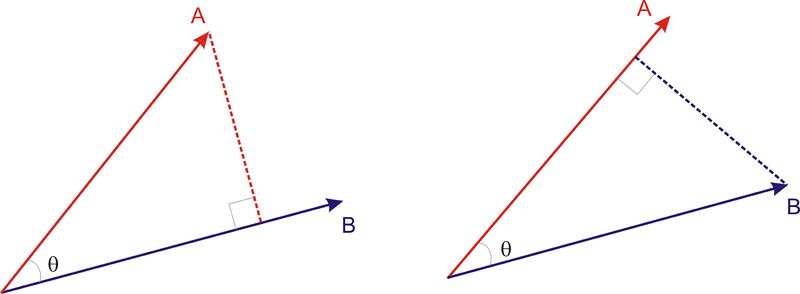
  ::AB+AxBx+AyBy+AzBz+... AxBx+AyBy+AzBz+...

  播放段落

  Another way to describe the process is to say that the dot product is the multiplication of one vector by the component of a second vector which is parallel to the first vector. In the diagram below are two vectors, A and B . A perpendicular line has been drawn radially outward from B towards A to create a right triangle with A as the hypotenuse.
  ::描述该过程的另一种方式是说点产品是第二个矢量的成分乘以与第一个矢量平行的第二个矢量。在下图中,有两个矢量A和B。一个垂直直径线从B向A方向直线向外拉,以创建一个右三角形,以A为下限。

  

  播放段落

  The component of $\begin{array}{r}\stackrel{\to }{A}\end{array}$ which is parallel to $\begin{array}{r}\stackrel{\to }{B}\end{array}$ is given by A cos θ so the second way to compute the dot product is $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=\stackrel{\to }{A}(\stackrel{\to }{B}\text{cos}\theta )=|\stackrel{\to }{A}||\stackrel{\to }{B}|\text{cos}\theta \end{array}$
  ::与B平行的A的成分由 A 给出, 所以计算点产品的第二种方法是 ABAA(BC) ABCC

  播放段落

  Likewise, the component of $\begin{array}{r}\stackrel{\to }{B}\end{array}$ which is parallel to $\begin{array}{r}\stackrel{\to }{A}\end{array}$ is given by B cos θ , so the dot product $\begin{array}{r}\stackrel{\to }{B}\times \stackrel{\to }{A}=|\stackrel{\to }{B}|(|\stackrel{\to }{A}|\text{cos}\theta )=|\stackrel{\to }{A}||\stackrel{\to }{B}|\text{cos}\theta \end{array}$
  ::同样,与A平行的B的成分由B提供,所以圆点产品BABB(AC)ABCC

  播放段落

  No matter which of the two vectors we "project" onto the other, the value of the dot product is maximized when the two vectors are parallel and zero when the two vectors are perpendicular to one another. When a vector is dotted with itself, the result is the square of the vector's magnitude since, by definition, a vector has the same direction as an equal vector.
  ::无论两个矢量中我们“预测”到另一个,当两个矢量平行时,点产品的价值最大化,当两个矢量相互垂直时,点产品的价值最大化,当两个矢量相互垂直时,点值最大化。当一个矢量本身被点点时,结果就是矢量星度的平方,因为根据定义,矢量的方向与相等矢量的方向相同。

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{A}=|\stackrel{\to }{A}|(|\stackrel{\to }{A}|\text{cos}\theta )=|\stackrel{\to }{A}||\stackrel{\to }{A}|\text{cos}0=|\stackrel{\to }{A}{|}^2\end{array}$
  ::

  播放段落

  Naturally the dot product of any vector with a zero vector is zero since the magnitude of the zero vector is 0.
  ::自然,任何矢量的零矢量的点产物为零,因为零矢量的大小为0。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a question about Kelly, who is studying the effect of wind on a flying plane.
  ::之前有人问你凯莉的事 他正在研究风对飞行飞机的影响

  播放段落

  Kelly is learning about flying airplanes so she can apply to take her pilot's exam. She is supposed to describe the added "push" effect a NE wind of 50 mph would have on a plane traveling at 30 mph due NE relative the ground. How can she describe the combination of forces in the NE direction?
  ::Kelly正在学习飞行飞机, 以便申请参加飞行员考试。 她应该描述在飞机上50米长的NE风在30米长的飞机上加上的“ 推推”效应, 因为NE与地面相对。 她如何描述NE方向的力量组合?

  播放段落

  Kelly could calculate the dot product of the two vectors and use the result to describe the total "push" in the NE direction.
  ::Kelly可以计算两个矢量的点产物, 并用结果来描述 NE 方向上的“ 推进” 总计 。

  播放段落

  Example 2
  ::例2

  播放段落
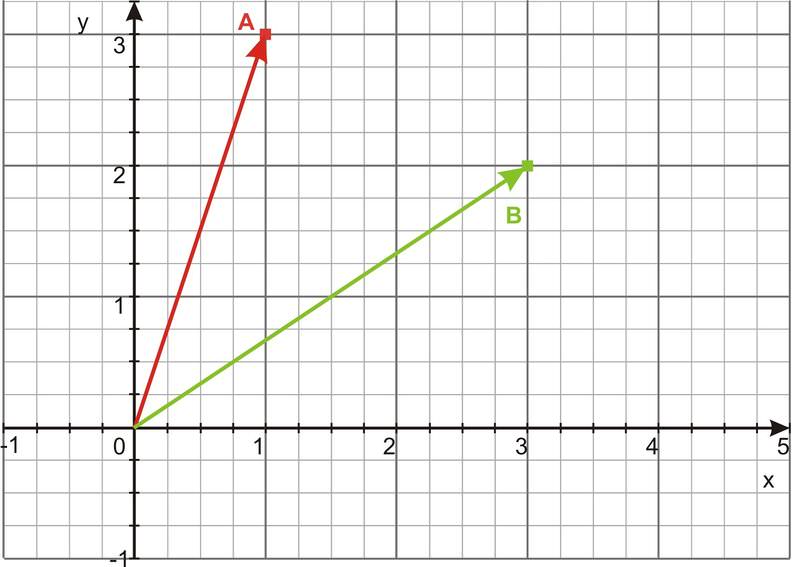
  1. Calculate the dot product of the two vectors shown below.
     ::计算以下两个矢量的点产物。

  播放段落

  First, we will use the components of the two vectors to determine the dot product.
  ::首先,我们将使用这两种矢量的成分来确定点产品。

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=A_x{B}_x+A_y{B}_y=(1\cdot 3)+(3\cdot 2)=3+6=9\end{array}$
  ::BAxBx+AyBy=(1)3+(3)2=3+6=9

  播放段落
  2. Determine the angle between the two vectors. $\begin{array}{r}\stackrel{\to }{A}=⟨1,3⟩\end{array}$ and $\begin{array}{r}\stackrel{\to }{B}=⟨3,2⟩\end{array}$ .
     ::确定两个矢量之间的角。

  

  播放段落

  Now that we know the dot product, the alternative definition of the dot product, $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|A||B|\text{cos}\theta \end{array}$ to find θ, the angle between the vectors.
  ::现在我们知道点产物, 点产物的替代定义, ABABBCos os 来寻找 , 矢量之间的角。

  播放段落

  First, find the magnitudes of the two vectors:
  ::首先,发现两个矢量的大小:

  播放段落

  $\begin{array}{r}|A|=\sqrt{{A_x}^2+{A_y}^2}=\sqrt{1^2+3^2}=\sqrt{1+9}=\sqrt{10}\end{array}$
  ::AAx2+Ay2=12+32=1+9=10

  播放段落

  $\begin{array}{r}|B|=\sqrt{{B_x}^2+{B_y}^2}=\sqrt{3^2+2^2}=\sqrt{9+4}=\sqrt{13}\end{array}$
  ::@BBx2+By2=32+22=9+4=13

  播放段落

  Then use these magnitudes with the cosine version of the dot product to find θ.
  ::然后用这些星等与点产品的余弦版来查找 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|A||B|\text{cos}\theta \end{array}$
  ::

  播放段落

  $\begin{array}{r}9=\sqrt{10}\sqrt{13}\text{cos}\theta \end{array}$
  ::9=1013 COs _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  $\begin{array}{r}\text{cos}\theta =\frac{9}{\sqrt{130}}=\frac{9}{11.4}=0.78935\end{array}$
  ::9130=911.4=0.78935

  $\begin{array}{r}\theta ={37.9}^{\circ }\end{array}$

  播放段落

  Example 3
  ::例3

  播放段落

  Calculate the dot product of the two vectors shown below. Then determine the angle between the two vectors.
  ::计算以下两个矢量的点产物。然后确定两个矢量之间的角。

  

  播放段落

  Use the components of the two vectors to determine the dot product.
  ::使用两个矢量的组件确定点产品。

  播放段落

  Here $\begin{array}{r}\stackrel{\to }{A}=⟨2,3⟩\end{array}$ and $\begin{array}{r}\stackrel{\to }{B}=⟨3,-1⟩\end{array}$ .
  ::这里是A2,3和B3,3 -1。

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=A_x{B}_x+A_y{B}_y=(2\cdot 3)+(3\cdot -1)=6+(-3)=3\end{array}$
  ::ABAxBx+AyBy=(23)+(31)=6+(3)=3

  播放段落

  Now to find the angle between the vectors, first find the magnitudes of the two vectors:
  ::现在要找到矢量之间的角, 首先找到两个矢量的大小 :

  播放段落

  $\begin{array}{r}|A|=\sqrt{{A_x}^2+{A_y}^2}=\sqrt{2^2+3^2}=\sqrt{4+9}=\sqrt{13}\end{array}$
  ::AAx2+Ay2=22+32=4+9=13

  播放段落

  $\begin{array}{r}|B|=\sqrt{{B_x}^2+{B_y}^2}=\sqrt{3^2+(-1{)}^2}=\sqrt{9+1}=\sqrt{10}\end{array}$
  ::BBx2+By2=32+(-1)2=9+1=10

  播放段落

  Then use these magnitudes with the cosine version of the dot product to find θ.
  ::然后用这些星等与点产品的余弦版来查找 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|A||B|\text{cos}\theta \end{array}$
  ::

  播放段落

  $\begin{array}{r}3=\sqrt{10}\sqrt{13}\text{cos}\theta \end{array}$
  ::3=1013 cos __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  $\begin{array}{r}\text{cos}\theta =\frac{3}{\sqrt{130}}=\frac{3}{11.4}=0.26312\end{array}$
  ::COs = 3130=311.4=0.2.6312

  $\begin{array}{r}\theta ={74.7}^{\circ }\end{array}$

  播放段落

  Example 4
  ::例4

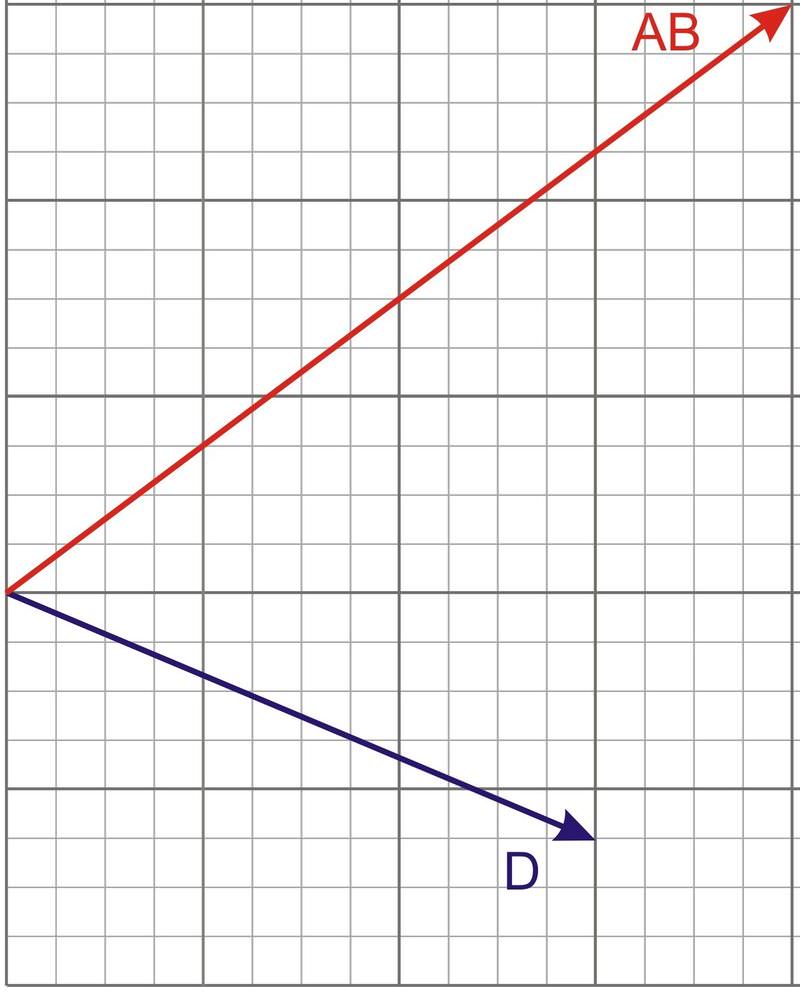
  播放段落

  The diagram below shows both vectors AB and D together on the same grid. Determine the of vector AB onto the direction of vector D .
  ::下图显示在同一网格上两个矢量的 AB 和 D 并列。确定矢量 AB 到 矢量 D 方向的矢量 AB 。

  播放段落

  To find the scalar projection onto the direction of another vector we need to know the unit vector in the direction of vector D .
  ::要找到向另一个矢量方向的斜线投影 我们需要了解向矢量D方向的单位矢量。

  播放段落

  First, the components of $\begin{array}{r}\stackrel{\to }{D}\end{array}$ are
  ::首先,D__的构成部分是:

  播放段落

  $\begin{array}{r}\stackrel{\to }{D}=⟨3,-1.25⟩\end{array}$
  ::D3,-1.25

  播放段落

  Now the magnitude of $\begin{array}{r}\stackrel{\to }{D}\end{array}$ is
  ::现在DQ的大小是

  播放段落

  $\begin{array}{r}|D|=\sqrt{(D_x{)}^2+(D_y{)}^2}=\sqrt{3^2+(-1.25{)}^2}=\sqrt{9+1.5625}=\sqrt{10.5625}\end{array}$ $\begin{array}{r}=3.25\end{array}$
  ::D(Dx)2+(Dy)2=32+(- 1. 252)=9+1. 5625=10. 5625=3. 25

  播放段落

  Finally, the direction vector of $\begin{array}{r}\stackrel{\to }{D}\end{array}$ is
  ::最后,D的方向矢量是

  播放段落

  $\begin{array}{r}\stackrel{\to }{D}=\frac{\stackrel{\to }{D}}{|D|}=\frac{3\hat{x}+(-1.25)\hat{y}}{3.25}=\frac{3}{3.25}\hat{x}+\frac{-1.25}{3.25}\hat{y}\end{array}$ .
  ::DD3x(- 1. 25y3. 25= 33. 25 x 1. 2. 2.5 x 1. 2. 2.5 y ) 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{D}=⟨0.923,-0.385⟩\end{array}$
  ::D0.923,-0.385

  播放段落

  Now we can use the dot-product to calculate the scalar projection of AB onto the direction of vector D .
  ::现在我们可以使用点产品来计算 AB 向矢量 D 方向的 ACAL 投影。

  播放段落

  $\begin{array}{r}\stackrel{\to }{AB}\times \stackrel{\to }{D}=(3\cdot 0.923)+(4\cdot -0.385)+(0\cdot 0)=2.769+(-1.54)=1.23\end{array}$
  ::AB ×D(30.923)+(40.385)+(00)= 2.769+(-1.54)=1.23

  

  播放段落

  Example 5
  ::例5

  播放段落

  Determine the dot product of two vectors $\begin{array}{r}\stackrel{\to }{E}=⟨14,8.5,21⟩\end{array}$ and $\begin{array}{r}\stackrel{\to }{G}=⟨15,12.4,-3.7⟩\end{array}$ . Then determine the angle between the two vectors.
  ::确定两个矢量E14、8.5、21和G15、12.4、-3.7之间的圆点产物。然后确定两个矢量之间的角。

  播放段落

  The dot product of two vectors is defined in two ways: $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=A_x{B}_x+A_y{B}_y+A_z{B}_z+...\end{array}$ and $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|A||B|\text{cos}\theta \end{array}$ . We will use the first to calculate the dot product and then we will use that result together with the second definition to determine the angle between the two vectors.
  ::两种矢量的点产物定义有两种方式:ABAxBx+AyBy+AzBz+...和ABABCos 。我们将使用第一种计算点产物,然后将使用该结果和第二个定义来确定两个矢量之间的角。

  播放段落

  $\begin{array}{r}\stackrel{\to }{E}\times \stackrel{\to }{G}=E_x{G}_x+E_y{G}_y+E_z{G}_z\end{array}$
  ::EQEXGx+EyGy+EzGz

  播放段落

  $\begin{array}{r}\stackrel{\to }{E}\times \stackrel{\to }{G}=(14)(15)+(8.5)(12.4)+(21)(-3.7)=210+105.4-77.7=237.7\end{array}$
  ::EG(14)(15)+(8.5)(12.4)+(21)(-3.7)=210+105.4-77.7=237.7

  播放段落

  To find the angle between the two vectors, we need to know not only the dot product of the two vectors, but also the length of each individual vector.
  ::要找到两个矢量之间的角,我们不仅要知道两个矢量的点产物,还要知道每个矢量的长度。

  播放段落

  $\begin{array}{r}|\stackrel{\to }{E}|=\sqrt{E_x^2+E_y^2+E_z^2}=\sqrt{(14{)}^2+(8.5{)}^2+(21{)}^2}=\sqrt{196+72.25+441}\end{array}$ $\begin{array}{r}=\sqrt{709.25}=26.63\end{array}$
  ::@EEx2+Ey2+Ez2=(142+(8.5)2+(212=196+72.25+441=709.25=26.63)

  播放段落

  $\begin{array}{r}|\stackrel{\to }{G}|=\sqrt{G_x^2+G_y^2+G_z^2}=\sqrt{(15{)}^2+(12.4{)}^2+(-3.7{)}^2}=\sqrt{225+153.76+13.69}\end{array}$ $\begin{array}{r}=\sqrt{392.45}=19.81\end{array}$
  ::@GGx2+Gy2+Gy2+Gz2=(152+(12.4)2+(-3.7)2=225+153.76+13.69=392.45=19.81

  播放段落

  Now use the second definition of the dot product to determine the angle
  ::现在使用点产品的第二个定义来确定角

  播放段落

  $\begin{array}{r}\stackrel{\to }{E}\times \stackrel{\to }{G}=|E||G|cos\theta \end{array}$
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

  播放段落

  $\begin{array}{r}\text{cos}\theta =\frac{\stackrel{\to }{E}\times \stackrel{\to }{G}}{|E||G|}=\frac{237.7}{(26.63)(19.81)}=\frac{237.7}{527.54}=0.45058\end{array}$
  ::287.7(26.63)(19.81)=237.7527.54=0.45058

  播放段落

  $\begin{array}{r}\theta ={\text{cos}}^{-1}(0.45058)={63.2}^{\circ }\end{array}$
  ::*cos-1(0.45058)=63.2

  播放段落

  Example 6
  ::例6

  播放段落

  Determine the dot product of the following two vectors.
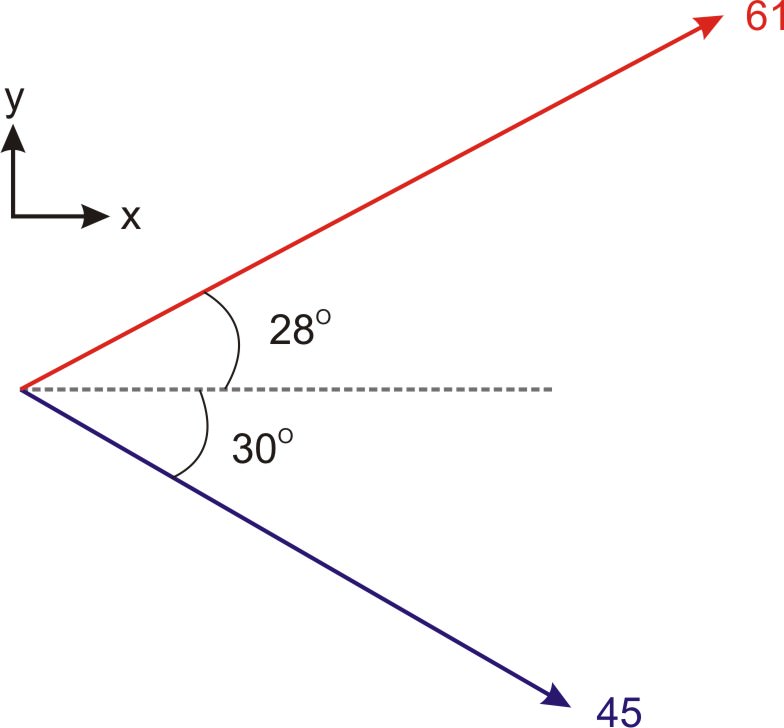
  ::确定以下两个矢量的点产物。

  

  播放段落

  The angle form of the dot product is given by $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|\stackrel{\to }{A}||\stackrel{\to }{B}|\text{cos}\theta \end{array}$ . In this case,
  ::点产品的角度形式由 ABABCos 提供。 在这种情况下,

  播放段落

  $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|\stackrel{\to }{A}||\stackrel{\to }{B}|\text{cos}\theta =(61)(45)\text{cos}58=2745\text{cos}58=1455\end{array}$
  ::BABCos (61)(45)cos 58=2745cos 58=1455

  播放段落

  Example 7
  ::例7

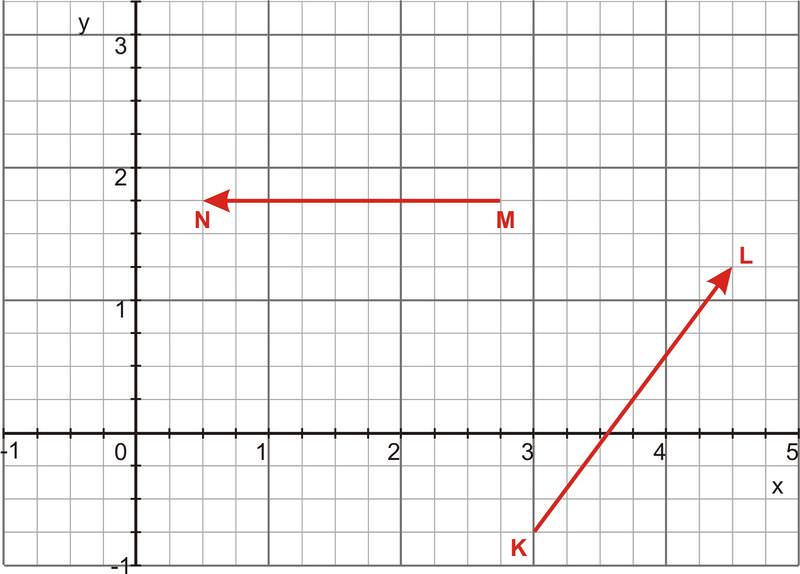
  播放段落

  Determine the angle between the vectors $\begin{array}{r}\stackrel{\to }{MN}\end{array}$ and $\begin{array}{r}\stackrel{\to }{KL}\end{array}$ .
  ::确定矢量 MN 和 KL 之间的角。

  

  播放段落

  First, we need to calculate the dot product of $\begin{array}{r}\stackrel{\to }{MN}\end{array}$ and $\begin{array}{r}\stackrel{\to }{KL}\end{array}$ :
  ::首先,我们需要计算MN和KL的点产物:

  播放段落

  $\begin{array}{r}\stackrel{\to }{MN}\times \stackrel{\to }{KL}=(MN{)}_x(KL{)}_x+(MN{)}_y(KL{)}_y+(MN{)}_z(KL{)}_z\end{array}$ $\begin{array}{r}=(2.25)(1.5)+(2)(0)+(0)(0)\end{array}$ $\begin{array}{r}=3.375\end{array}$
  ::MNKL(MN)x(KL)x+(MN)y(KL)y +(MN)z(KL)z=(2.25)(1.5)+(2)(0)+(0)(0)=3.375

  播放段落

  We can then use the definition $\begin{array}{r}\stackrel{\to }{MN}\times \stackrel{\to }{KL}=|\stackrel{\to }{MN}||\stackrel{\to }{KL}|\text{cos}\theta \end{array}$ to determine the angle between the two vectors. But first we need to determine the magnitudes of the two vectors.
  ::然后我们可以使用定义 MNQKLMNKL com 来决定两个矢量之间的角。 但是首先我们需要确定两个矢量的大小 。

  播放段落

  $\begin{array}{r}|\stackrel{\to }{MN}|=\sqrt{(MN{)}_x^2+(MN{)}_y^2+(MN{)}_z^2}=\sqrt{(-2.25{)}^2+(0{)}^2+(0{)}^2}\end{array}$ $\begin{array}{r}=2.25\end{array}$
  ::* *%(MN)x2+(MN)y2+(MN)z2=(-2.25)2+(0)2+(0)2+(0)2=2.25

  播放段落

  $\begin{array}{r}|\stackrel{\to }{KL}|=\sqrt{(KL{)}_x^2+(KL{)}_y^2+(KL{)}_z^2}=\sqrt{(1.5{)}^2+(2{)}^2+(0{)}^2}=\sqrt{2.25+4+0}\end{array}$ $\begin{array}{r}=\sqrt{6.25}=2.5\end{array}$
  ::KL(KL)x2+(KL)y2+(KL)y2+(KL)z2=(1.5)2+(2)2+(0)2=2.25+4+0=6.25=2.5

  播放段落

  $\begin{array}{r}\text{cos}\theta =\frac{\stackrel{\to }{MN}\times \stackrel{\to }{KL}}{|\stackrel{\to }{MN}||\stackrel{\to }{KL}|}=\frac{3.375}{(2.25)(2.5)}=\frac{3.375}{5.625}=0.6\end{array}$
  ::3.3775(2.25)(2.5)=3.3755.625=0.6

  播放段落

  $\begin{array}{r}\theta ={\text{cos}}^{-1}(-0.6)={53.1}^{\circ }\end{array}$
  ::cos-1 (-0.6) = 53.1

  播放段落

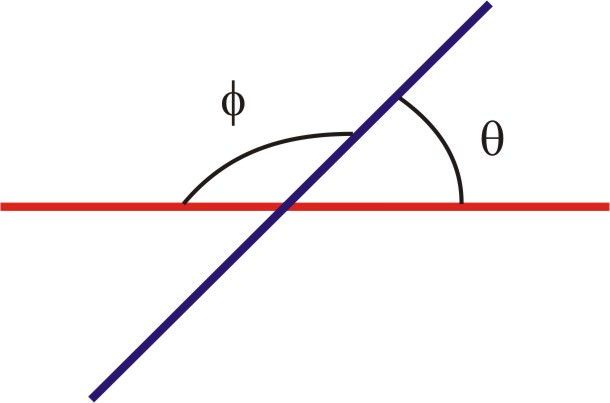
  By looking at the diagram, we can see that the angle between these two vectors is larger than 90 ^o . Many calculators only give the smaller of the two angles between two lines. As you can see below, both θ and $\begin{array}{r}\varphi \end{array}$ relate the blue line to the red line.
  ::通过查看图表,我们可以看到这两个矢量之间的角大于90o。许多计算器只给出两个线之间的两个角中较小的角。从下面可以看到, 和 将蓝线与红线联系起来。

  

  播放段落

  For our problem, the calculator returned a value of 53.1 ^o . The actual angle between the two vectors is 180 ^o - 53.1 ^o = 126.9 ^o when we take into account the directions of $\begin{array}{r}\stackrel{\to }{MN}\end{array}$ and $\begin{array}{r}\stackrel{\to }{KL}\end{array}$ .
  ::对于我们的问题,计算器返回了53.1o。当我们考虑到MNQ和KLQ方向时,两种矢量之间的实际角度是180o-53.1o=126.9o。

  播放段落

  Review
  ::回顾

  播放段落
  1. What is the magnitude of $\begin{array}{r}⟨-9,3⟩\end{array}$ ?
     ::9,3的幅度是多少?
  播放段落
  2. What is the magnitude of $\begin{array}{r}⟨-3,16⟩\end{array}$ ?
     ::3,16的幅度是多少?
  播放段落
  3. What is the magnitude of $\begin{array}{r}⟨6,18⟩\end{array}$ ?
     ::6,18的幅度是多少?
  播放段落
  4. What is the magnitude of $\begin{array}{r}⟨9,10⟩\end{array}$ ?
     ::9,10的幅度是多少?

  播放段落
  5. What is the direction of $\begin{array}{r}⟨-10,10⟩\end{array}$ ?
     ::10点10分的方向是什么?
  播放段落
  6. What is the direction of $\begin{array}{r}⟨9,17⟩\end{array}$ ?
     ::九点十七分的方向是什么?
  播放段落
  7. What is the direction of $\begin{array}{r}⟨2,17⟩\end{array}$ ?
     ::2,17"的方向是什么?
  播放段落
  8. What is the direction of $\begin{array}{r}⟨-6,12⟩\end{array}$ ?
     ::6点12点的方向是什么?

  播放段落

  Find: a) The dot product of Vectors A and B, and b) The measure of the angle found between the vectors, rounded to the nearest degree.
  ::查找a) 矢量A和B的点产物,和(b) 矢量之间所发现角的测量值,四舍五入至最接近的度。

  播放段落
  9. Vector A = $\begin{array}{r}-2i+5j\end{array}$ and Vector B = $\begin{array}{r}-3i+5j\end{array}$
     ::矢量A=-2i+5j和矢量B=-3i+5j
  播放段落
  10. Vector A = $\begin{array}{r}⟨6,13⟩\end{array}$ and Vector B = $\begin{array}{r}⟨9,10⟩\end{array}$
      ::矢量A = 6,13 和 矢量B = 9,10
  播放段落
  11. Vector A = $\begin{array}{r}⟨4,5⟩\end{array}$ and Vector B = $\begin{array}{r}⟨-4,8⟩\end{array}$
      ::矢量A = 4,5 和 矢量B = 4,8
  播放段落
  12. Vector A = $\begin{array}{r}-7i+4j\end{array}$ and Vector B = $\begin{array}{r}6i+3j\end{array}$
      ::矢量A=-7i+4j和矢量B=6i+3j
  播放段落
  13. Vector A = $\begin{array}{r}⟨-9,15⟩\end{array}$ and Vector B = $\begin{array}{r}⟨-7,11⟩\end{array}$
      ::矢量A = 9,15 和 矢量B = 7,11
  播放段落
  14. Vector A = $\begin{array}{r}⟨1,18⟩\end{array}$ and Vector B = $\begin{array}{r}⟨1,6⟩\end{array}$
      ::矢量 A = 1,18 和 矢量 B = 1,6
  播放段落
  15. Vector A = $\begin{array}{r}4i+11j\end{array}$ and Vector B = $\begin{array}{r}3i+14j\end{array}$
      ::矢量A=4i+11j和矢量B=3i+14j
  播放段落
  16. Prove that $\begin{array}{r}\stackrel{\to }{C}=2\hat{i}+5\hat{j}+2\hat{k}\end{array}$ and $\begin{array}{r}\stackrel{\to }{D}=3\hat{i}-2\hat{j}+2\hat{k}\end{array}$ are perpendicular by showing their dot product is zero.
      ::证明C*2i5j2k 和D*3i2j2kare 穿透性 显示他们的点产品为零。
  播放段落
  17. Explain why showing the dot product of two vectors is zero proves they are perpendicular.
      ::解释为什么显示两个矢量的圆点产物为零 证明它们是垂直的。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。