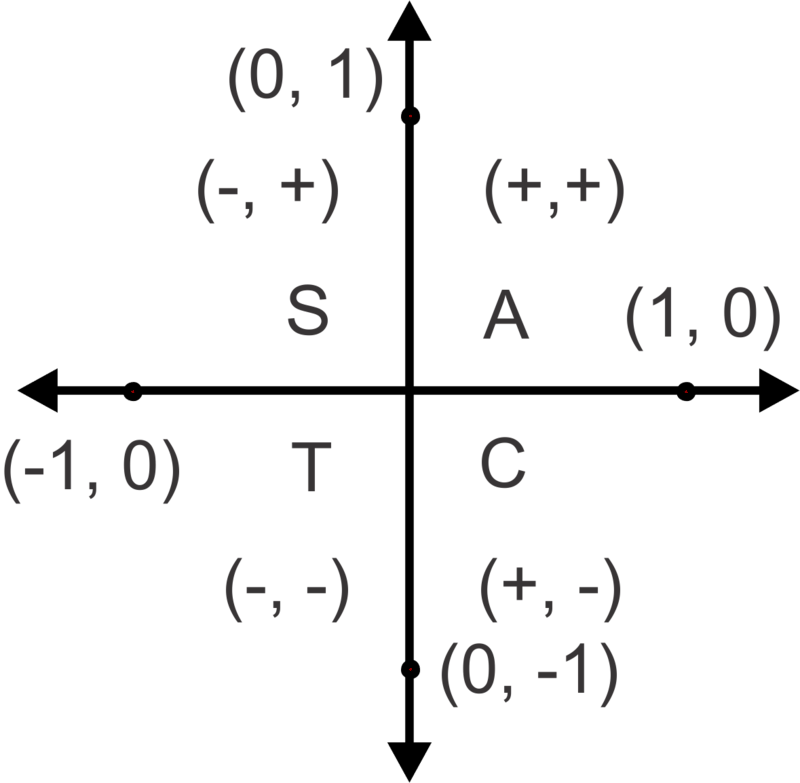13.7 单圆圆的三角比

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 单位圆圆的三角比

  Collapse Expand

  单位圆圆的三角比

  播放段落

  What are the exact values of the following trigonometric functions ?
  ::以下三角函数的确切值是多少?

  播放段落
  1. $\begin{array}{r}\cos {495}^{\circ }\end{array}$
     ::COS495
  播放段落
  2. $\begin{array}{r}\tan \frac{5\pi }{3}\end{array}$
     ::{\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F2F

  播放段落

  Trigonometric Ratios on the Unit Circle
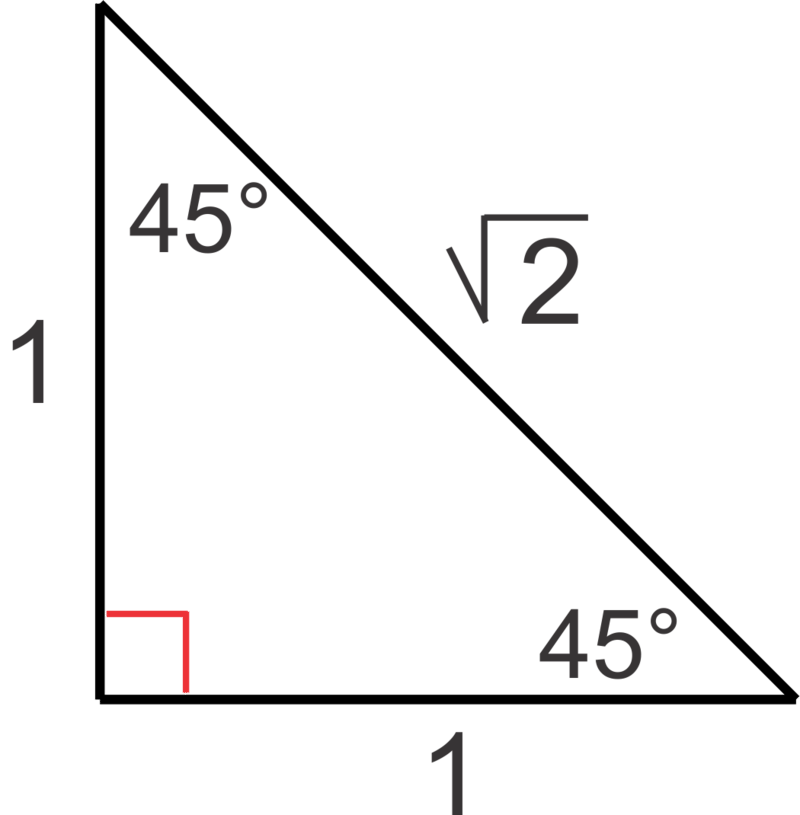
  ::单位圆圆的三角比

  播放段落

  Recall special right triangles from Geometry. In a $\begin{array}{r}({30}^{\circ }-{60}^{\circ }-{90}^{\circ })\end{array}$ triangle, the sides are in the ratio $\begin{array}{r}1:\sqrt{3}:2\end{array}$ .
  ::回顾几何中的特殊右三角。在( 306090) 三角形中,两边的比值为1: 3: 2。

  播放段落

  In an isosceles triangle $\begin{array}{r}({45}^{\circ }-{45}^{\circ }-{90}^{\circ })\end{array}$ , the congruent sides and the hypotenuse are in the ratio $\begin{array}{r}1:1:\sqrt{2}\end{array}$ .
  ::在等分三角形(45454590)中,相近边和下限在1:1:2的比率中。

  

  播放段落

  In a $\begin{array}{r}({30}^{\circ }-{60}^{\circ }-{90}^{\circ })\end{array}$ triangle, the sides are in the ratio $\begin{array}{r}1:\sqrt{3}:2\end{array}$ .
  ::在(306090)三角形中,两边的比例为1:3比2。

  

  播放段落

  Now let’s make the hypotenuse equal to 1 in each of the triangles so we’ll be able to put them inside the unit circle . Using the appropriate ratios, the new side lengths are:
  ::现在让我们把三角形的下限等于每个三角形的1,这样我们就能够把它们放入单位圆内。 用适当的比率,新的侧边长度是:

  

  

  播放段落

  Using these triangles, we can evaluate sine, cosine and tangent for each of the angle measures.
  ::使用这些三角形,我们可以评估每个角度测量的正弦、正弦、正弦和正正弦。

  播放段落

  $$\begin{array}{rl}& \sin {45}^{\circ }=\frac{\sqrt{2}}{2}\sin {60}^{\circ }=\frac{\sqrt{3}}{2}\sin {30}^{\circ }=\frac{1}{2}\\ & \cos {45}^{\circ }=\frac{\sqrt{2}}{2}\cos {60}^{\circ }=\frac{1}{2}\cos {30}^{\circ }=\frac{\sqrt{3}}{2}\\ & \tan {45}^{\circ }=1\tan {60}^{\circ }=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}\tan {30}^{\circ }=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{2}\end{array}$$

  
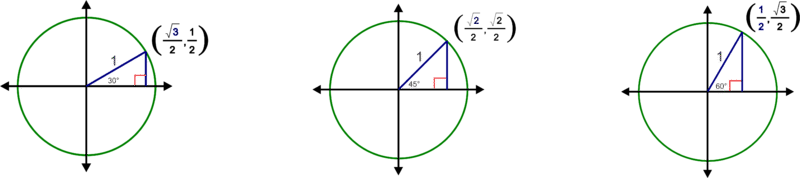
  ::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

  播放段落

  These triangles can now fit inside the unit circle.
  ::这些三角形现在可以融入单位圆圈。

  

  播放段落

  Putting together the trigonometric ratios and the coordinates of the points on the circle, which represent the lengths of the legs of the triangles, $\begin{array}{r}(\mathrm{\Delta }x,\mathrm{\Delta }y)\end{array}$ , we can see that each point is actually $\begin{array}{r}(\cos \theta ,\sin \theta )\end{array}$ , where $\begin{array}{r}\theta \end{array}$ is the reference angle . For example, $\begin{array}{r}\sin {60}^{\circ }=\frac{\sqrt{3}}{2}\end{array}$ is the $\begin{array}{r}y\end{array}$ – coordinate of the point on the unit circle in the triangle with reference angle $\begin{array}{r}{60}^{\circ }\end{array}$ . By reflecting these triangles across the axes and finding the points on the axes, we can find the trigonometric ratios of all multiples of $\begin{array}{r}{0}^{\circ },{30}^{\circ }\end{array}$ and $\begin{array}{r}{45}^{\circ }\end{array}$ (or $\begin{array}{r}0,\frac{\pi }{6},\frac{\pi }{4}\end{array}$ radians).
  ::将三角比和圆上各点的坐标( x, y)放在一起, 代表三角形腿的长度( x, y), 我们可以看到每个点实际上是( cos, sin) 的参考角度。 例如, sin6032 是三角形圆单位圆点的坐标, 以及参考角度 60。 通过在轴上反射这些三角形, 并在轴上找到点, 我们能找到所有倍数的三角比, 即 0, 30 和 45 ( or 0, 6, 4 弧度) 。

  播放段落

  Let's solve the following problems using the unit circle.
  ::让我们用单位圆来解决以下的问题。

  播放段落
  1. Find $\begin{array}{r}\sin \frac{3\pi }{2}\end{array}$ .
     ::找寻罪孽... 32 。

  播放段落

  Find $\begin{array}{r}\frac{3\pi }{2}\end{array}$ on the unit circle and the corresponding point is $\begin{array}{r}(0,-1)\end{array}$ . Since each point on the unit circle is $\begin{array}{r}(\cos \theta ,\sin \theta ),\sin \frac{3\pi }{2}=-1\end{array}$ .
  ::在单位圆上查找 32, 相应的点是 (0, - 1) 。 因为单位圆上的每个点是 (cos, sin) , sin32 1 。

  播放段落
  2. Find $\begin{array}{r}\tan \frac{7\pi }{6}\end{array}$ .
     ::寻找 ten\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

   This time we need to look at the ratio $\begin{array}{r}\frac{\sin \theta }{\cos \theta }\end{array}$ . We can use the unit circle to find $\begin{array}{r}\sin \frac{7\pi }{6}=-\frac{1}{2}\end{array}$ and $\begin{array}{r}\cos \frac{7\pi }{6}=-\frac{\sqrt{3}}{2}\end{array}$ . Now, $\begin{array}{r}\tan \frac{7\pi }{6}=\frac{-\frac{1}{2}}{-\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\end{array}$ .
  ::这一次我们需要查看比例 sin612 和 cos7632。 现在, tan7612- 32=13=33。

  播放段落

  Quadrants in a Unit Circle
  ::单圆圆的方形

  播放段落

  Another way to approach these exact value problems is to use the reference angles and the special right triangles. The benefit of this method is that there is no need to memorize the entire unit circle. If you memorize the special right triangles, can determine reference angles and know where the ratios are positive and negative you can put the pieces together to get the ratios. Looking at the unit circle above, we see that all of the ratios are positive in Quadrant I, sine is the only positive ratio in Quadrant II, tangent is the only positive ratio in Quadrant III and cosine is the only positive ratio in Quadrant IV.
  ::处理这些精确值问题的另一种方式是使用参考角度和特殊右三角。 这种方法的好处是, 不需要将整个单位圆重新命名。 如果您记住了特别右三角, 可以确定参考角度, 并且知道参考比例是正负的, 您可以将碎片放在一起来获得比率。 查看上面的单位圆, 我们看到在 Quadrant I 中所有比率都是正的, Sinr 是 Quadrant II 中唯一的正比, 切线是 Quadrant III 中唯一的正比, 而 Cosine 是 Quadrant IV 中唯一的正比 。

  播放段落

  Keeping this diagram in mind will help you remember where cosine, sine and tangent are positive and negative. You can also use the pneumonic device - A ll S tudents T ake C alculus, or ASTC , to recall which is positive (all the others would be negative) in which quadrant.
  ::记住这个图表会帮助您记住正负正正正正正正正正正正正正正正正向向向。 您也可以使用气动设备 - 所有学生都使用微积分, 或 ASTTC 来回忆正负的( 所有其他人都是负负的) 。

  播放段落

  The coordinates on the vertices will help you determine the ratios for the multiples of $\begin{array}{r}{90}^{\circ }\end{array}$ or $\begin{array}{r}\frac{\pi }{2}\end{array}$ .
  ::顶端的坐标将帮助您确定 90 或% 2 的倍数比率 。

  

  播放段落

  Now, let's find the exact values for the following trigonometric functions using the alternative method.
  ::现在,让我们用替代方法 找到以下三角函数的精确值。

  播放段落
  1. $\begin{array}{r}\cos {120}^{\circ }\end{array}$
     ::120

  播放段落

  First, we need to determine in which quadrant the angles lies. Since $\begin{array}{r}{120}^{\circ }\end{array}$ is between $\begin{array}{r}{90}^{\circ }\end{array}$ and $\begin{array}{r}{180}^{\circ }\end{array}$ it will lie in Quadrant II. Next, find the reference angle. Since we are in QII, we will subtract from $\begin{array}{r}{180}^{\circ }\end{array}$ to get $\begin{array}{r}{60}^{\circ }\end{array}$ . We can use the reference angle to find the ratio, $\begin{array}{r}\cos {60}^{\circ }=\frac{1}{2}\end{array}$ . Since we are in QII where only sine is positive, $\begin{array}{r}\cos {120}^{\circ }=-\frac{1}{2}\end{array}$ .
  ::首先, 我们需要确定角度所在的方位 。 由于 120 介于 90 至 180 之间, 它将位于 Quadrant II 。 下一步, 找到参考角度 。 既然我们在 QII , 我们将从 180 中减去 60 。 我们可以使用 参考角度来找到比例 , 共 = 60 12 。 既然我们在 QII 中, 只有正弦值, 共 = 120 12 。

  播放段落
  2. $\begin{array}{r}\sin \frac{5\pi }{3}\end{array}$
     ::问题53

  播放段落

  This time we will need to work in terms of radians but the process is the same. The angle $\begin{array}{r}\frac{5\pi }{3}\end{array}$ lies in QIV and the reference angle is $\begin{array}{r}\frac{\pi }{3}\end{array}$ . This means that our ratio will be negative. Since $\begin{array}{r}\sin \frac{\pi }{3}=\frac{\sqrt{3}}{2},\sin \frac{5\pi }{3}=-\frac{\sqrt{3}}{2}\end{array}$ .
  ::这一次我们需要在弧度方面工作,但过程是一样的。 角度 5+3 位于 QIV , 参考角度是 ++3 。 这意味着我们的比例将是负的。 因为 sin%3 = 32, sin%5Q3 = 32 。

  播放段落
  3. $\begin{array}{r}\tan \frac{7\pi }{2}\end{array}$
     ::72

  播放段落

  The angle $\begin{array}{r}\frac{7\pi }{2}\end{array}$ represents more than one entire revolution and it is equivalent to $\begin{array}{r}2\pi +\frac{3\pi }{2}\end{array}$ . Since our angle is a multiple of $\begin{array}{r}\frac{\pi }{2}\end{array}$ we are looking at an angle on an axis. In this case, the point is $\begin{array}{r}(0,-1)\end{array}$ . Because $\begin{array}{r}\tan \theta =\frac{\sin \theta }{\cos \theta },\tan \frac{7\pi }{2}=\frac{-1}{0}\end{array}$ , which is undefined. Thus, $\begin{array}{r}\tan \frac{7\pi }{2}\end{array}$ is undefined.
  ::角度 72 代表一个以上的整个革命, 相当于 232 。 由于我们的角度是% 2 的倍数, 我们所看到的是一个轴上的一个角度。 在此情况下, 点是 (0, - 1) 。 因为 tansincos , tan7210 尚未定义 。 因此, tan 72 未定义 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find  the exact values of the following trigonometric ratios.
  ::早些时候,你被要求找到以下三角比率的准确值。

  播放段落
  1. $\begin{array}{r}\cos {495}^{\circ }\end{array}$
     ::COS495

  播放段落

  First, we need to determine in which quadrant the angle lies. Since $\begin{array}{r}{495}^{\circ }-{360}^{\circ }={135}^{\circ }\end{array}$ is between $\begin{array}{r}{90}^{\circ }\end{array}$ and $\begin{array}{r}{180}^{\circ }\end{array}$ it will lie in Quadrant II. Next, find the reference angle. Since we are in QII, we will subtract from $\begin{array}{r}{180}^{\circ }\end{array}$ to get $\begin{array}{r}{45}^{\circ }\end{array}$ . We can use the reference angle to find the ratio, $\begin{array}{r}\cos {45}^{\circ }=\frac{\sqrt{2}}{2}\end{array}$ . Since we are in QII where only sine is positive, $\begin{array}{r}\cos {495}^{\circ }=-\frac{\sqrt{2}}{2}\end{array}$ .
  ::首先, 我们需要确定角度所在的方位 。 由于 495 360 135 介于 90 至 180 之间, 它将位于 Quadrant II 。 下一步, 找到参考角度 。 由于我们在 QII , 我们将从 180 中减去 45 。 我们可以使用 参考角度来找到比例 , cos 45 22 。 既然我们是在 QII 中, 只有正弦是正的, cos 495 22 。

  播放段落
  2. $\begin{array}{r}\tan \frac{5\pi }{3}\end{array}$
     ::{\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F2F

  播放段落

  In p roblem #2 above  we established that the angle $\begin{array}{r}\frac{5\pi }{3}\end{array}$ lies in QIV and the reference angle is $\begin{array}{r}\frac{\pi }{3}\end{array}$ . This means that the tangent ratio will be negative. Since $\begin{array}{r}\tan \frac{\pi }{3}=\sqrt{3},\tan \frac{5\pi }{3}=-\sqrt{3}\end{array}$ .
  ::在上文问题2中,我们确定角度5Q3位于QIV, 参考角度为 Q3。 这意味着正切比为负。 从 tanQ3 = 3, tanQ5Q3 3 开始 。

  播放段落

  Find the exact trigonometric ratios. You may use either method.
  ::找到精确的三角比。 您可以使用两种方法 。

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{array}{r}\cos \frac{7\pi }{3}\end{array}$
  ::COS=73

  播放段落

  $\begin{array}{r}\frac{7\pi }{3}\end{array}$   has a reference angle of $\begin{array}{r}\frac{\pi }{3}\end{array}$ in QI. $\begin{array}{r}\cos \frac{\pi }{3}=\frac{1}{2}\end{array}$ and since cosine is positive in QI, $\begin{array}{r}\cos \frac{7\pi }{3}=\frac{1}{2}\end{array}$ .
  ::7+3 在 QI. cos=3=12中参考角为%3, 由于 QI 的余弦正弦值为%7Q3=12。

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{array}{r}\tan \frac{9\pi }{2}\end{array}$
  ::{\pos(192,2)\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F2F2

  播放段落

  $\begin{array}{r}\frac{9\pi }{2}\end{array}$ is coterminal to $\begin{array}{r}\frac{\pi }{2}\end{array}$ which has coordinates (0, 1). So $\begin{array}{r}\tan \frac{9\pi }{2}=\frac{\sin \frac{9\pi }{2}}{\cos \frac{9\pi }{2}}=\frac{1}{0}\end{array}$ which is undefined.
  ::9% 2 与有座标( 0, 1) 的 % 2 相交, 坐标为 # 2, 坐标为 0, 坐标为 0. 1 , 所以 tan 92 =sin = @ 92cos @ 92 = 10 未定义 。

  播放段落

  Example 4
  ::例4

  播放段落

  $\begin{array}{r}\sin {405}^{\circ }\end{array}$
  ::-405 -405 -405

  播放段落

  $\begin{array}{r}{405}^{\circ }\end{array}$ has a reference angle of $\begin{array}{r}{45}^{\circ }\end{array}$ in QI. $\begin{array}{r}\sin {45}^{\circ }=\frac{\sqrt{2}}{2}\end{array}$ and since sine is positive in QI, $\begin{array}{r}\sin {405}^{\circ }=\frac{\sqrt{2}}{2}\end{array}$ .
  ::405的参考角度在QI中为454522, QI中为正弦, Sin40522。

  播放段落

  Example 5
  ::例5

  播放段落

  $\begin{array}{r}\tan \frac{11\pi }{6}\end{array}$
  ::tan116

  播放段落

  $\begin{array}{r}\frac{11\pi }{6}\end{array}$ is coterminal to $\begin{array}{r}\frac{\pi }{6}\end{array}$ in QIV. $\begin{array}{r}\tan \frac{\pi }{6}=\frac{\sqrt{3}}{3}\end{array}$ and since tangent is negative in QIV, $\begin{array}{r}\tan \frac{11\pi }{6}=-\frac{\sqrt{3}}{3}\end{array}$ .
  ::QIV. tan6=33中,116同6是共同的,而且由于QIV, tan11633中正切值为负。

  播放段落

  Example 6
  ::例6

  播放段落

  $\begin{array}{r}\cos \frac{2\pi }{3}\end{array}$
  ::COs%23

  播放段落

  $\begin{array}{r}\frac{2\pi }{3}\end{array}$ is coterminal to $\begin{array}{r}\frac{\pi }{3}\end{array}$ in QII. $\begin{array}{r}\cos \frac{\pi }{3}=\frac{1}{2}\end{array}$ and since cosine is negative in QII, $\begin{array}{r}\cos \frac{2\pi }{3}=\frac{1}{2}\end{array}$ .
  ::23在 QII. cos 3= 12 中为%3, 并且由于在 QII 中为负余, com#23= 12 。

  播放段落

  Review
  ::回顾

  播放段落

  Find the exact values for the following trigonometric functions.
  ::查找以下三角函数的确切值。

  播放段落
  1. $\begin{array}{r}\sin \frac{3\pi }{4}\end{array}$
     ::三、四、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、九、十、九、九、九、九、九、九、九、九、九、九、九、九、九、
  播放段落
  2. $\begin{array}{r}\cos \frac{3\pi }{2}\end{array}$
     ::COs=32
  播放段落
  3. $\begin{array}{r}\tan {300}^{\circ }\end{array}$
     ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不,不,不,不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不
  播放段落
  4. $\begin{array}{r}\sin {150}^{\circ }\end{array}$
     ::150
  播放段落
  5. $\begin{array}{r}\cos \frac{4\pi }{3}\end{array}$
     ::CO=43
  播放段落
  6. $\begin{array}{r}\tan \pi \end{array}$
     ::丹纳
  播放段落
  7. $\begin{array}{r}\cos \left(-\frac{15\pi }{4}\right)\end{array}$
     ::COs(- 154)
  播放段落
  8. $\begin{array}{r}\sin {225}^{\circ }\end{array}$
     ::确实如此... . 225 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
  播放段落
  9. $\begin{array}{r}\tan \frac{7\pi }{6}\end{array}$
     ::76
  播放段落
  10. $\begin{array}{r}\sin {315}^{\circ }\end{array}$
      ::31511111111111111111111111111111111111111111111113111111113111111111111111111111111111111111111111111111111
  播放段落
  11. $\begin{array}{r}\cos {450}^{\circ }\end{array}$
      ::450
  播放段落
  12. $\begin{array}{r}\sin \left(-\frac{7\pi }{2}\right)\end{array}$
      :-72)
  播放段落
  13. $\begin{array}{r}\cos \frac{17\pi }{6}\end{array}$
      ::COS%176
  播放段落
  14. $\begin{array}{r}\tan {270}^{\circ }\end{array}$
      ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不!
  播放段落
  15. $\begin{array}{r}\sin (-{210}^{\circ })\end{array}$
      : - 210 )

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。