5.6 交叉产品

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 交叉产品

  Collapse Expand

  交叉产品

  播放段落

  are related to in a number of ways. Both are vector calculations, both are related not only to the magnitude of each vector, but also to the relative directions of both vectors.
  ::两者都是矢量计算,不仅与每种矢量的大小有关,而且与两种矢量的相对方向有关。

  播放段落

  Dot products in a sense calculate the joined force of two vectors in a given direction, and so are greatest when the vectors are parallel. Cross products, however, are greatest when the vectors are perpendicular... what then do they calculate?
  ::圆点产品在某种意义上计算两个矢量在特定方向的结合力, 当矢量平行时最大。 但是, 当矢量垂直时, 交叉产品最大... 它们计算什么?

  播放段落

  Cross Products
  ::交叉产品

  播放段落

  Whereas a dot product of two vectors produces a scalar value; the cross product of the same two vectors produces a vector quantity having a direction perpendicular to the original two vectors.
  ::两个矢量的点产物产生一个天平值;同一两个矢量的交叉产物产生一个矢量,其方向与原来的两个矢量垂直。

  播放段落

  The cross product of two vector quantities is another vector whose magnitude varies as the angle between the two original vectors changes. The cross product is sometimes referred to as the vector product of two vectors. The magnitude of the cross product represents the area of the parallelogram whose sides are defined by the two vectors, as shown in the figure below. Therefore, the maximum value for the cross product occurs when the two vectors are perpendicular to one another, but when the two vectors are parallel to one another the magnitude of the cross product is equal to zero.
  ::两个矢量的交叉产物是另一个矢量,其数量随两个原始矢量之间的角变化而不同。交叉产物有时被称为两个矢量的矢量产物。交叉产物的大小代表由两个矢量定义的平行图的面积,如下图所示。因此,交叉产物的最大值出现在两个矢量相互垂直时,但当两个矢量相互平行时,交叉产物的大小等于零。

  

  播放段落

  The algebraic form of the cross product equation is more complicated than that for the dot product. For two 3D vectors $\begin{align*}\overrightarrow{A}\end{align*}$ and $\begin{align*}\overrightarrow{B}\end{align*}$ ,
  ::跨产品方程式的代数形式比点产品更为复杂。

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle (A_2 B_3 - A_3 B_2),(A_3 B_1 - A_1 B_3), (A_1 B_2 - A_2 B_1)\right \rangle\end{align*}$
  ::B(A2B3-A3B2),(A3B1-A1B3),(A1B2-A2B1)

  播放段落

  Another way to describe the process is to say that the cross product is the multiplication of one vector by the component of the other vector which is perpendicular to the first vector. In the diagram below are two vectors, A and B . A perpendicular line has been drawn radially outward from B towards A to create a right triangle with A as the hypotenuse.
  ::描述该过程的另一种方式是说,交叉产品是另一个矢量的成分乘以另一个矢量的乘法,而另一个矢量与第一个矢量是垂直的。在下图中,两个矢量是A和B。一个垂直的直线从B向A向外被直线划出,以建立一个右三角形,以A为下限。

  

  播放段落

  The component of $\begin{align*}\overrightarrow{A}\end{align*}$ which is perpendicular to $\begin{align*}\overrightarrow{B}\end{align*}$ is given by A sin θ so the magnitude of the cross product can be written as $\begin{align*}| \overrightarrow{A} \times \overrightarrow{B} | = \overrightarrow{A} (\overrightarrow{B} \mbox{sin}\ \theta) = | \overrightarrow{A} | | \overrightarrow{B} | \ \mbox{sin}\ \theta\end{align*}$
  ::与BQQQ的直角的A的成分是由罪孽所赋予的 这样,交叉产品的大小就可以写成 ABAA(Bsin ) ABSin BSin ABSin

  播放段落

  The direction of the cross product is perpendicular to the plane defined by the two crossed vectors. For example, the cross product of two vectors in the x-y plane will be parallel to the z-axis. This still leaves two possible directions for the cross product, though: either $\begin{align*}+ \hat{z}\end{align*}$ or $\begin{align*}-\hat{z}\end{align*}$ .
  ::交叉产品的方向与两个交叉矢量所定义的平面是垂直的,例如,x-y平面上两个矢量的交叉产品将与z轴平行。这仍然为交叉产品留下两个可能的方向:+z或-z。

  播放段落

  We use a right-hand-rule to indicate the direction of the cross product. Position the thumb and index finger of your right hand with the first vector along your thumb and the second vector along your index finger. Your middle finger, when extended perpendicular to your palm, will indicate the direction of the cross product of the two vectors.
  ::我们使用右手法则来指示交叉产物的方向。 右手的拇指和食指与第一个矢量放在拇指上, 第二个矢量在你的食指上。 您的中手指, 当伸展到您的手掌上时, 将指示两个矢量的交叉产物的方向 。

  

  播放段落

  As you can see in the diagram above, $\begin{align*}\overrightarrow{A} \times \overrightarrow{B}\end{align*}$ is along $\begin{align*}+\hat{z}\end{align*}$ (coming up out of the page) while $\begin{align*}\overrightarrow{B} \times \overrightarrow{A}\end{align*}$ is along $\begin{align*}-\hat{z}\end{align*}$ (going down into the page) and $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = - \overrightarrow{B} \times \overrightarrow{A}\end{align*}$
  ::如上图所示,AB和A和A和A和A和B和B和A和+z(正从页面中浮出),而BA和B和Z和Z和B和B和B和A和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和B和A和B和B和B和B和B和B和B和B和A和B和B和B和B和B和B和B和B和B和B和B。

  播放段落

  The Normal Vector
  ::普通矢量

  播放段落

  We can use the cross product and the definition of the unit vector to determine the direction which is perpendicular to a plane.
  ::我们可以使用交叉产品和单位矢量的定义来确定与飞机相关的方向。

  播放段落

  In general, we can define a normal vector, $\begin{align*}\hat{n}\end{align*}$ , which has a unity magnitude (i.e. magnitude equal to one) and which is perpendicular to a plane occupied by a pair of vectors, U and V .
  ::总而言之,我们可以定义一个正常的矢量,即n,它具有统一级(即等于1的量),与一对矢量(U和V)所占用的平面是垂直的。

  播放段落

  $\begin{align*}\hat{n} = \frac{\overrightarrow{U} \times \overrightarrow{V}} {|\overrightarrow{U} \times \overrightarrow{V}|}\end{align*}$
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Calculate the cross product of the two vectors shown below.
  ::计算以下两个矢量的交叉产品。

  

  播放段落

  Use the components of the two vectors to determine the cross product.
  ::使用两个矢量的组件确定交叉产品。

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle (A_y B_z - A_z B_y), (A_zB_x - A_x B_z), (A_x B_y - A_y B_x)\right \rangle\end{align*}$
  ::B(AyBz-AzBy),(AzBx-AxBz),(AxBy-AyBx)

  播放段落

  Since these two vectors are both in the x-y plane, their own z-components are both equal to 0 and the vector product will be parallel to the z axis.
  ::由于这两种矢量都存在于X-y平面上,因此它们自己的Z成分均等于0,而矢量产品将与z轴平行。

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle [(3 \cdot 0) - (0 \cdot 2)], [(0 \cdot -4) - (2.5 \cdot 0)], [(2.5 \cdot 2) - (3 \cdot -4)]\right \rangle\end{align*}$
  ::[(30)-(02),[(04)-(2.50)],[(2.52)-(34)]

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle [(0) - (0)], [(0) - (0)], [(5) - (-12)]\right \rangle = \left \langle 0,0,(5 + 12)\right \rangle = \left \langle 0,0,17\right \rangle\end{align*}$
  ::[0)-(0)],[0)-(0)],[5)-(12)],[5)-(12)] 0,0,0,(5+12)-(0)-0,0,17]

  播放段落

  We can check our answer using the sine version of the cross product, but first we need to know the angle between the two vectors. We can use the dot product to find θ. First use the components to find the dot product.
  ::我们可以使用交叉产品的正弦版本来检查答案, 但是首先我们需要知道两个矢量之间的角。 我们可以使用点产品来找到 。 首先使用部件来找到点产品 。

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = A_x B_x + A_y B_y + A_z B_z = (2.5 * -4) + (3 * 2) + (0 * 0) = -10 + 6 + 0 =\end{align*}$ $\begin{align*}-4\end{align*}$
  ::ABAxBx+AyBy+AzBz=(2.54)+(3*2)+(0*0)+(10+6+04)

  播放段落

  Then find the magnitudes of the two vectors:
  ::然后发现两个矢量的大小:

  播放段落

  $\begin{align*}| \overrightarrow{A} | = \sqrt{A^2_x + A^2_y + A^2_z} = \sqrt{2.5^2 + 3^2 + 0^2} = \sqrt{6.25 + 9 + 0} = \sqrt{15.25}\end{align*}$
  ::AAx2+Ay2+Az2=2.52+32+02=6.25+9+0=15.25

  播放段落

  $\begin{align*}| \overrightarrow{B} | = \sqrt{B^2_x + B^2_y + B^2_z} = \sqrt{(-4)^2 + 2^2 + 0^2} = \sqrt{16 + 4 + 0} = \sqrt{20}\end{align*}$
  ::@BBx2+By2+Bz2=(-4)2+22+02=16+4+0=20

  播放段落

  Then use these magnitudes with the cosine version of the dot product to find θ.
  ::然后用这些星等与点产品的余弦版来查找 。

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = | A | | B |\ \mbox{cos}\ \theta\end{align*}$
  ::

  播放段落

  $\begin{align*}-4 = \sqrt{15.25} \sqrt{20}\ \mbox{cos}\ \theta\end{align*}$
  ::- 4=15.2520 COs ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  $\begin{align*}\mbox{cos}\ \theta = \frac{-4} {\sqrt{305}} \approx \frac{-4} {17.5} = -0.229\end{align*}$
  ::4305417.50.229

  $\begin{align*}\theta = 103^\circ\end{align*}$

  播放段落

  Now use the sine of this angle and the two magnitudes to determine the cross product:
  ::现在使用这个角度的正弦值和两个大小来确定交叉产品 :

  播放段落

  $\begin{align*}| \overrightarrow{A} \times \overrightarrow{B} | = | \overrightarrow{A} | | \overrightarrow{B} | \ \mbox{sin}\ \theta\end{align*}$
  ::

  播放段落

  $\begin{align*}| \overrightarrow{A} \times \overrightarrow{B} | = \sqrt{15.25} \sqrt{20}\ \mbox{sin}\ 103^\circ = \sqrt{305}\ \mbox{sin}\ 103^\circ = 17\end{align*}$
  ::AB15.2520 罪 103305 罪 10317

  播放段落

  This is the same answer that we obtained from the component notation, which is good. We use the right-hand rule to determine the direction of the vector product. If you place your thumb along vector A and your forefinger along vector B , your middle finger will point along $\begin{align*}+\hat{z}\end{align*}$ and $\begin{align*}| \overrightarrow{A} \times \overrightarrow{B} | = \left \langle 0, 0, 17\right \rangle\end{align*}$
  ::这是我们从构件符号中获取的同样答案, 这是很好的。 我们使用右手规则来确定矢量产品的方向。 如果您在矢量 A 上放拇指, 在矢量 B 上放食指, 您的中指将指向 +z 和 B0, 0, 17 。

  播放段落

  Example 2
  ::例2

  播放段落

  The diagram shows two vectors A and B which define a plane passing through the origin. Use these two vectors to determine the normal vector to this plane. $\begin{align*}\overrightarrow{A} = \left \langle 3, 0, 4\right \rangle\end{align*}$ and $\begin{align*}\overrightarrow{B} = \left \langle 5, 10, 0\right \rangle\end{align*}$
  ::该图显示两个矢量 A 和 B 来定义通过源的平面。 使用这两个矢量来确定此平面的正常矢量 。 A 3, 0, 4 和 B 5, 10,0 和 B 5, 10 。

  播放段落

  The normal vector is defined by
  ::通常矢量由

  播放段落

  $\begin{align*}\hat{n} = \frac{\overrightarrow{U} \times \overrightarrow{V}} {|\overrightarrow{U} \times \overrightarrow{V}|}\end{align*}$
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不

  播放段落

  In this case, we obtain
  ::在这种情况下,我们获得

  播放段落

  $\begin{align*}\hat{n} = \frac{\overrightarrow{A} \times \overrightarrow{B}} {|\overrightarrow{A} \times \overrightarrow{B}|}\end{align*}$
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

  播放段落

  Use the component version of the cross-product equation to find the components of $\begin{align*}\overrightarrow{A} \times \overrightarrow{B}\end{align*}$
  ::使用跨产品方程式的元件版本查找 AB的元件

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle (A_y B_z - A_z B_y), (A_z B_x - A_x B_z), (A_x B_y - A_y B_x)\right \rangle\end{align*}$
  ::B(AyBz-AzBy),(AzBx-AxBz),(AxBy-AyBx)

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle [(0 \cdot 0) - (4 \cdot 10)], [(4 \cdot 5) - (3 \cdot 0)], [(3 \cdot 10) - (0 \cdot 5)]\right \rangle\end{align*}$
  ::[(0)0-(4)10],[(4)5]-(3)0)],[(3)(10)-(0)5]

  播放段落

  $\begin{align*}\overrightarrow{A} \times \overrightarrow{B} = \left \langle (0 - 40), (20 - 0), (30 - 0)\right \rangle = \left \langle -40, 20, 30\right \rangle\end{align*}$
  ::================================================================================================================================================================================================================================================================================================================================================== ==========================================================================================================================================================================

  播放段落

  Next, calculate the magnitude of the cross product, $\begin{align*}| \overrightarrow{A} \times \overrightarrow{B}|\end{align*}$
  ::下一步,计算交叉产品的大小, AB。

  播放段落

  $\begin{align*}| \overrightarrow{A} \times \overrightarrow{B}| = \sqrt{(-40)^2 + 20^2 + 30^2} = \sqrt{1600 + 400 + 900} = \sqrt {2900} =\end{align*}$ $\begin{align*}53.8516\end{align*}$
  ::AB(- 402)+202+302=1600+400+900+900=2900=53.8516

  播放段落

  $\begin{align*}\hat{n} = \frac{\overrightarrow{A} \times \overrightarrow{B}} {|\overrightarrow{A} \times \overrightarrow{B}|} = \frac{\left \langle -40, 20, 30\right \rangle} {53.9} = \left \langle \frac{-40} {53.9}, \frac{20} {53.9}, \frac{30} {53.9}\right \rangle = \left \langle -0.743, 0.371, 0.557\right \rangle\end{align*}$
  ::-=YTET -伊甸园字幕组=- 翻译:

  播放段落

  Example 3
  ::例3

  播放段落

  Determine the cross product $\begin{align*}\overrightarrow{F} \times \overrightarrow{r}\end{align*}$ for the two vectors $\begin{align*}\overrightarrow{F} = \left \langle 2, 3, 4\right \rangle\end{align*}$ and $\begin{align*}\overrightarrow{r} = \left \langle 7, 6, 5\right \rangle\end{align*}$ . Then use the cross product to determine the angle between the two vectors.
  ::确定两个矢量的交叉产品FrF2,3,4和r7,6,5。然后使用交叉产品确定两个矢量之间的角。

  播放段落

  One of the two ways to determine the magnitude of the cross product of two vectors uses the components of the two vectors:
  ::确定两种矢量的交叉产品规模的两种方法之一使用两种矢量的成分:

  播放段落

  $\begin{align*}\overrightarrow{F} \times \overrightarrow{r} = \left \langle (F_y r_z - F_z r_y), (F_z r_x - F_x r_z),(F_x r_y - F_y r_x)\right \rangle\end{align*}$
  ::Fór(Fyrz-Fzry),(Fzrx-Fxrz),(Fxry-Fyrx)_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  $\begin{align*}\overrightarrow{F} \times \overrightarrow{r} = \left \langle(3 \cdot 5 - 4 \cdot 6), (4 \cdot 7 - 2 \cdot 5), (2 \cdot 6 - 3 \cdot 7)\right \rangle = \left \langle(15 - 24), (28 - 10), (12 - 21)\right \rangle\end{align*}$
  ::Fr(35-46),(47-25),(26-37) (15～24),(28～10),(12～21) (12～21)

  播放段落

  $\begin{align*}\overrightarrow{F} \times \overrightarrow{r} = \left \langle -9, 18, -9 \right \rangle\end{align*}$
  ::Fr9,18,-99

  播放段落

  Now we can use the cross product and the second definition of the cross product to determine the angle between the two vectors.
  ::现在我们可以使用交叉产品和交叉产品的第二个定义来确定两个矢量之间的角。

  播放段落

  $\begin{align*}| \overrightarrow{F} \times \overrightarrow{r} | = | F | | r | \ \mbox{sin}\ \theta\end{align*}$
  ::{\fn华文楷体\fs16\1cHE0E0E0}罪孽

  播放段落

  We need to calculate the magnitudes of the vectors and of the cross product.
  ::我们需要计算矢量和交叉产品的数量。

  播放段落

  $\begin{align*}| \overrightarrow{F} | = \sqrt{F^2_x + F^2_y + F^2_z} = \sqrt{2^2 + 3^2 + 4^2} = \sqrt{ 4 + 9 + 16} = \sqrt{29} = 5.385\end{align*}$
  ::@FFx2+Fy2+Fz2=22+32+42=4+9+16=29=5.385

  播放段落

  $\begin{align*}| \overrightarrow{r}| = \sqrt{r^2_x + r^2_y + r^2_z} = \sqrt{7^2 + 6^2 + 5^2} = \sqrt{49 + 36 + 25} = \sqrt{110} =\end{align*}$ $\begin{align*}10.488\end{align*}$
  ::rrx2+ry2+rz2=72+62+52=49+36+25=110=10.488

  播放段落

  $\begin{align*}| \overrightarrow{F} \times \overrightarrow{r}| = \sqrt{(-9)^2 + 18^2 + (-9)^2} = \sqrt{81 + 324 + 81} = \sqrt{486} = 22.0454\end{align*}$
  ::@Fr(- 9)2+182+(- 9)2=81+324+81=486=22.0454

  播放段落

  $\begin{align*}\mbox{sin}\ \theta = \frac{|\overrightarrow{F} \times \overrightarrow{r}|} {| F | | r |} = \frac{22.0454} {(5.385)(10.488)} = 0.390\end{align*}$
  ::-=0.390 -=====================================================================================================================================================================================================================

  播放段落

  $\begin{align*}\theta = \mbox{sin}^{-1} (0.390) = 22.98^\circ\end{align*}$
  ::=22.98\\\\\\\\\\\\1(0.390)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  We can use the dot product of the two vectors to check our solution.
  ::我们可以使用两个矢量的点产物来检查我们的解决方案。

  播放段落

  $\begin{align*}\overrightarrow{F} \times \overrightarrow{r} = |\overrightarrow{F}| |\overrightarrow{r}| \mbox{cos}\ \theta\end{align*}$
  ::

  播放段落

  $\begin{align*}\overrightarrow{F} \times \overrightarrow{r} = F_x r_x + F_y r_y + F_z r_z = 2*7 + 3*6 + 4*5 = 14 + 18 + 20 = 52\end{align*}$
  ::FrFxrx+Fyry+Fzrz=2*7+3*6+4*5=14+18+20=52

  播放段落

  $\begin{align*}\mbox{cos}\ \theta = \frac{\overrightarrow{F} \times \overrightarrow{r}} {|\overrightarrow{F}| |\overrightarrow{r}|} = \frac{52} {(5.385)(10.488)} = 0.920714\end{align*}$
  ::=0.920714 (5.385) (10.488)=0.920714)

  播放段落

  $\begin{align*}\theta = \mbox{cos}^{-1} (0.920714) = 22.97\end{align*}$
  ::cos-1(0.920714)=22.97

  播放段落

  This answer matches our value from the cross product to within rounding variations.
  ::这一答案与我们从交叉产品到四舍五入差异的价值相符。

  播放段落

  Example 4
  ::例4

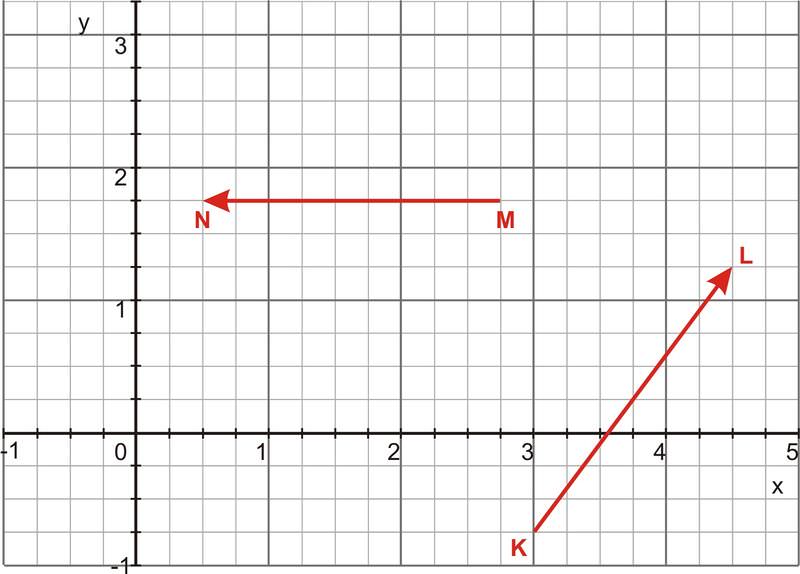
  播放段落

  Determine the magnitude of the cross product of the two vectors shown below.
  ::确定以下两个矢量的交叉产值。

  

  播放段落

  First we need to identify the components of the two vectors by using the information given on the graph. In this case, $\begin{align*}\overrightarrow{MN} = \left \langle -2.25, 0, 0\right \rangle\end{align*}$ and $\begin{align*}\overrightarrow{KL} = \left \langle 1.5, 2, 0\right \rangle\end{align*}$
  ::首先,我们需要使用图中提供的信息来识别两个矢量的成分。 在这种情况下, MN2.25,0,0 和 KL1.5,2,0。

  播放段落

  $\begin{align*}\overrightarrow{MN} \times \overrightarrow{KL} = \left \langle(MN_y KL_z- MN_z KL_y), (MN_z KL_x - MN_x KL_z), (MN_x KL_y - MN_y KL_x)\right \rangle\end{align*}$
  ::MNQKL(MNYKLZ-MNZKLy),(MNZKKLX-MNKKLz),(MNKKLY-MNKLx)

  播放段落

  $\begin{align*}\overrightarrow{MN} \times \overrightarrow{KL} = \left \langle(0 \cdot 0 - 0 \cdot 2), (0 \cdot 1.5 - (-2.25) \cdot 0), ((-2.25) \cdot 2 - 0 \cdot 1.5)\right \rangle\end{align*}$
  ::MNQKL(00-02,),(01.5-(-2.25)),(- 2.25),(- 2.25),(2)-2-01.5)

  播放段落

  $\begin{align*}\overrightarrow{MN} \times \overrightarrow{KL} = \left \langle0 - 0, 0 - 0, -4.5 - 0\right \rangle = \left \langle0, 0, -4.5\right \rangle\end{align*}$
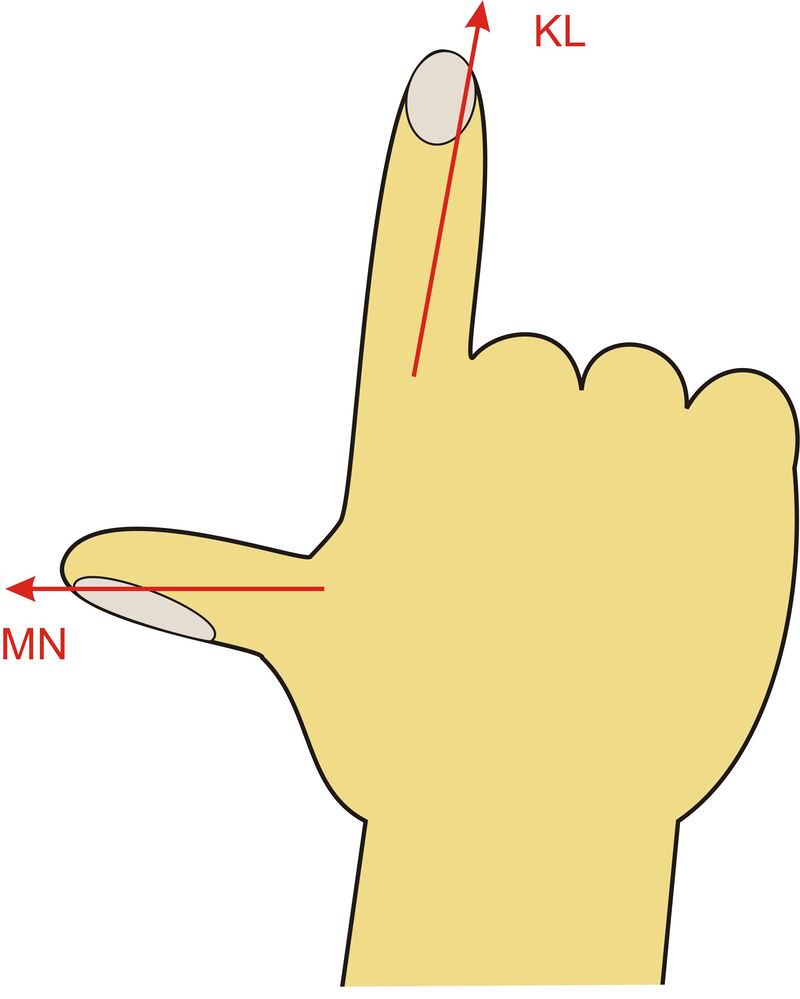
  ::MNKL0-00-00-4.5-00-00-4.5*

  播放段落

  As we can see by the components, this vector has a magnitude of 4.5 units and lies in the –z direction. We can also use the right-hand-rule to see the direction of the cross product. As shown in the figure below, if we align the right thumb with vector MN and the right fore-finger with vector KL, the palm and extended middle-finger point in the –z direction.
  ::正如我们从组件中可以看到的那样,该矢量的尺寸为4.5个单位,位于-z方向。我们也可以使用右手规则来查看交叉产品的方向。 如下图所示,如果我们将右拇指与矢量MN和右前指与矢量KL、棕榈和延伸中指点对齐,则右拇指与矢量MN和右前指对齐。

  

  播放段落

  Example 5
  ::例5

  播放段落

  A plane passing through the origin is defined by the two vectors, $\begin{align*}\overrightarrow{W} = \left \langle 4, 5, 2\right \rangle\end{align*}$ and $\begin{align*}\overrightarrow{L} = \left \langle 8, 1, 9\right \rangle\end{align*}$ . Determine the equation of a unit vector representing a direction perpendicular to this plane.
  ::飞经原体的平面由两个向量(W4,5,2和L8,1,9)确定。确定代表与该平面垂直方向的单位向量的方程。

  播放段落

  To solve this problem we need to use the definition of the normal vector $\begin{align*}\hat{n} = \frac{\overrightarrow{W} \times \overrightarrow{L}} {|\overrightarrow{W} \times \overrightarrow{L}|}\end{align*}$ , the component form of the definition of the cross product,
  ::为了解决这个问题,我们需要使用普通矢量的定义 nWLWLL, 即交叉产品定义的构成形式,

  播放段落

  $\begin{align*}\overrightarrow{W} \times \overrightarrow{L} = \left \langle(W_y L_z - W_z L_y), (W_z L_x - W_x L_z), (W_x L_y - W_y L_x)\right \rangle\end{align*}$ . In this case, we obtain
  ::W(WyLz-WzLy),(WzLx-WxLz),(WxLy-WyLx),(WxLy-WyLx)。

  播放段落

  $\begin{align*}\overrightarrow{W} \times \overrightarrow{L} = \left \langle(5 \cdot 9 - 2 \cdot 1),(2 \cdot 8 - 4 \cdot 9), (4 \cdot 1 - 5 \cdot 8)\right \rangle\end{align*}$
  ::W(59-21),(28-49),(41-58)

  播放段落

  $\begin{align*}\overrightarrow{W} \times \overrightarrow{L} = \left \langle(45 - 2),(16 - 36), (4 - 40)\right \rangle = \left \langle43, -20, -36\right \rangle\end{align*}$
  ::W(45-2),(16)-36,(4-40) 43,(20)-36

  播放段落

  We also need to know the magnitude of this cross product
  ::我们还需要了解这一跨产品的规模。

  播放段落

  $\begin{align*}|\overrightarrow{W} \times \overrightarrow{L}| = \sqrt{x^2 + y^2 + z^2} = \sqrt{(43)^2 + (-20)^2 + (-36)^2} = \sqrt{1849 + 400 + 1296} =\end{align*}$ $\begin{align*}\sqrt{3545} = 59.54\end{align*}$
  ::Lx2+y2+z2=(432+(-20)+(-36)2+(-36)2=1849+400+1296=3545=59。

  播放段落

  Now we can determine the normal vector
  ::现在我们可以确定正常矢量

  播放段落

  $\begin{align*}\hat{n} = \frac{\overrightarrow{W} \times \overrightarrow{L}} {| \overrightarrow{W} \times \overrightarrow{L}|} = \frac{\left \langle 43, -20, -36\right \rangle} {59.54} = \left \langle \frac{43} {59.54}, \frac{-20} {59.54}, \frac{-36} {59.54}\right \rangle = \left \langle 0.7222, -0.3359, -0.6046\right \rangle\end{align*}$
  ::==================================================================================================================================================== ========================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  Example 6
  ::例6

  播放段落

  Determine the area of a parallelogram whose sides are defined by the vectors $\begin{align*}\overrightarrow{w} = \left \langle 85, 89, 91\right \rangle\end{align*}$ and $\begin{align*}\overrightarrow{h} = \left \langle 67, 70, 88\right \rangle\end{align*}$ , lengths measured in centimeters.
  ::确定以厘米计测量的矢量(w85、89、91和h67、70、88)所定义的平行图的侧面区域。

  播放段落

  The area of the parallelogram whose sides are defined by a pair of vectors is equal to the magnitude of the cross product of the two vectors, $\begin{align*}|\overrightarrow{w} \times \overrightarrow{h}|\end{align*}$ . First we need to find the cross product of the two vectors:
  ::以一对矢量来定义其侧面的平行图区域与两种矢量的交叉产物(wh)的大小相等。 首先,我们需要找到两种矢量的交叉产物:

  播放段落

  $\begin{align*}\overrightarrow{w} \times \overrightarrow{h} = \left \langle(w_y h_z - w_z h_y), (w_z h_x - w_x h_z), (w_x h_y - w_y h_x)\right \rangle\end{align*}$
  ::wh(wyhz-wzhy),(wzhx-wxhz),(wxhy-wyhx)

  播放段落

  $\begin{align*}\overrightarrow{w} \times \overrightarrow{h} = \left \langle (89 \cdot 88 - 91 \cdot 70), (91 \cdot 67 - 85 \cdot 88), (85 \cdot 70 - 89 \cdot 67)\right \rangle\end{align*}$
  ::wh(89-88-91-70),(91-67-85-88),(85-70-89-67)

  播放段落

  $\begin{align*}\overrightarrow{w} \times \overrightarrow{h} = \left \langle (7832 - 6370), (6097 - 7480), (5950 - 5963)\right \rangle = \left \langle 1462, -1383, -13\right \rangle\end{align*}$
  ::wh(7832-6370),(6097-7480),(5950-5963) 1462,-1383,-13

  播放段落

  $\begin{align*}| \overrightarrow{w} \times \overrightarrow{h} | = \sqrt{x^2 + y^2 + z^2} = \sqrt{1462^2 + (-1383)^2 + (13)^2} = \sqrt{4050302} \approx\end{align*}$ $\begin{align*}2012.5\end{align*}$
  ::{whx2+y2+z2=14622+(-1383)2+(-1313)2+(-13)2=40503022012.5

  播放段落

  Since the lengths of the two vectors were measured in centimeters, the area of the parallelogram is 2013 cm ² measured to the nearest square centimeter.
  ::由于两个矢量的长度是以厘米测量的,平行图的面积是2013cm2,测量到最接近的平方厘米。

  播放段落

  Example 7
  ::例7

  播放段落

  Determine the cross product of the two vectors $\begin{align*}\overrightarrow{f} = \left \langle 3, 13, 11\right \rangle\end{align*}$ and $\begin{align*}\overrightarrow{g} = \left \langle 9, 6, 15\right \rangle\end{align*}$
  ::确定两个矢量的交叉产品f3,13,11和g9,6,15。

  播放段落

  $\begin{align*}\overrightarrow{f} \times \overrightarrow{g} = \left \langle(f_y g_z - f_z g_y), (f_z g_x - f_x g_z), (f_x g_y - f_y g_x)\right \rangle\end{align*}$
  ::fg*g*(fygz-fzgy),(fzgx-fxgz),(fxgy-fygx)

  播放段落

  $\begin{align*}\overrightarrow{f} \times \overrightarrow{g} = \left \langle(13 \cdot 15 - 11 \cdot 6), (11 \cdot 9 - 3 \cdot 15), (3 \cdot 6 - 13 \cdot 9)\right \rangle\end{align*}$
  ::-=YTET -伊甸园字幕组=- 翻译:

  播放段落

  $\begin{align*}\overrightarrow{f} \times \overrightarrow{g} = \left \langle(195 - 66), (99 - 45), (18 - 117)\right \rangle = \left \langle 129, 54, -99\right \rangle\end{align*}$
  :195-66),(99-45),(18-117),(129,54)-(99)

  播放段落

  Example 8
  ::例8

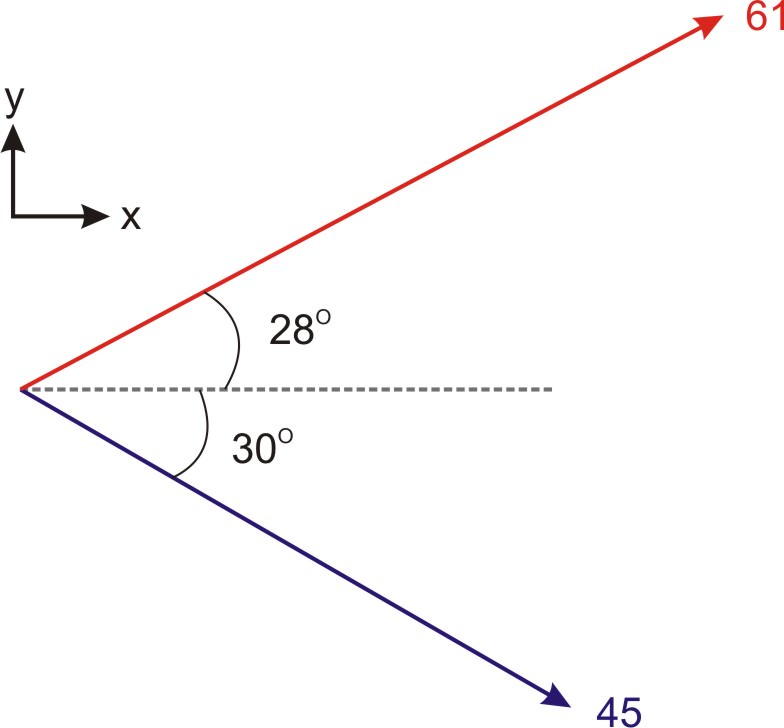
  播放段落

  Determine the magnitude of the cross-product of these two vectors.
  ::确定这两个矢量的交叉产品规模。

  

  播放段落

  Since we know the magnitudes of the two vectors and the angle between them, we can use the angle-version of the cross-product equation to determine the magnitude of the cross-product: $\begin{align*}|\overrightarrow{A} \times \overrightarrow{B}| = | \overrightarrow{A}| | \overrightarrow{B}| \ \mbox{sin}\ \theta = (61)(45) \mbox{sin}\ 58 = 2328\end{align*}$
  ::由于我们知道两个矢量的大小以及它们之间的角,我们可以使用交叉产品方程的角转换来确定交叉产品的规模: ABABBsin (61)(45)sin 58=2328

  播放段落

  Since these two vectors lie in the x-y plane, the direction of the cross-product will be parallel to the z-axis.
  ::由于这两个矢量位于X-y平面上,交叉产品的方向将与z轴平行。

  播放段落

  Review
  ::回顾

  播放段落

  Calculate the cross products:
  ::计算交叉产品 :

  播放段落
  1. Vectors c = $\begin{align*}-6i + 2j + 3k\end{align*}$ and a = $\begin{align*}-6i + 2j + 13k\end{align*}$
     ::矢量c = - 6i+2j+3k和 a = - 6i+2j+13k
  播放段落
  2. Vectors v = $\begin{align*}\left \langle-1,4,7\right \rangle\end{align*}$ and u = $\begin{align*}\left \langle -5,10,3\right \rangle\end{align*}$
     ::矢量 v=1,4,7和u =5,10,3
  播放段落
  3. Vectors f = $\begin{align*}-6i + 8j -6k\end{align*}$ and s = $\begin{align*}-3i + 15j + 19k\end{align*}$
     ::矢量f =-6i+8j-6k和s =-3i+15j+19k
  播放段落
  4. Vectors j = $\begin{align*}-3i + 15j -4k\end{align*}$ and t = $\begin{align*}7i + 10j + 6k\end{align*}$
     ::矢量j =- 3i+15j-4k和 t = 7i+10j+6k
  播放段落
  5. Vectors r = $\begin{align*}\left \langle3,13,-1\right \rangle\end{align*}$ and v = $\begin{align*} \left \langle7,6,1\right \rangle\end{align*}$
     ::矢量 r = 3,13,-1,和 v 7,6,1
  播放段落
  6. Vectors e = $\begin{align*}\left \langle-1,8,-3\right \rangle\end{align*}$ and a = $\begin{align*}\left \langle -2,1,19\right \rangle\end{align*}$
     ::矢量 e = 1,8,-3和 a = 2,1,19
  播放段落
  7. Vectors j = $\begin{align*}-3i + 17j + 6k\end{align*}$ and h = $\begin{align*}8i + 9j + 7k\end{align*}$
     ::矢量j = - 3i+17j+6k和h = 8i+9j+7k
  播放段落
  8. Vectors a = $\begin{align*}9i + 10j + 9k\end{align*}$ and g = $\begin{align*}-5i + 19j + 15k\end{align*}$
     ::矢量 a = 9i+10j+9k 和 g = 5i+19j+15k
  播放段落
  9. Vectors j = $\begin{align*}4i + 18j -8k\end{align*}$ and m = $\begin{align*}2i + j + 19k\end{align*}$
     ::矢量j = 4i+18j-8k和m = 2i+j+19k
  播放段落
  10. What is the cross product of $\begin{align*}\left \langle-2,1,-2\right \rangle\end{align*}$ and $\begin{align*}\left \langle5,6,9\right \rangle?\end{align*}$
      ::2,1,2-2和5,6,9的交叉产物是什么?
  播放段落
  11. Find a vector orthogonal to both $\begin{align*}\left \langle1,20,2\right \rangle\end{align*}$ and $\begin{align*}\left \langle4,2,3\right \rangle\end{align*}$
      ::查找一个矢量正对到 1,20,2和4,2,3。
  播放段落
  12. Vectors $\begin{align*}y = 5i + 6j + 6k\end{align*}$ and $\begin{align*}f = -4i + 9j + 3k.\end{align*}$ What is the area of the parallelogram formed by having y and f as adjacent sides?
      ::矢量 y= 5i+6j+6k 和 f4i+9j+3k。 以 y 和 f 作为相邻侧构成的平行图的区域是什么 ?
  播放段落
  13. What is the area of the parallelogram formed by having $\begin{align*}\left \langle-2,1,7\right \rangle\end{align*}$ and $\begin{align*}\left \langle5,7,16\right \rangle \end{align*}$ as adjacent sides?
      ::以2,1,7和5,7,16为邻边形成的平行图面积是多少?
  播放段落
  14. What is the cross product between $\begin{align*}\left \langle 8,6,8 \right \rangle\end{align*}$ and $\begin{align*}\left \langle 8,6,8 \right \rangle\end{align*}$ ?
      ::8,6,8和8,6,8之间的交叉产品是什么?
  播放段落
  15. Vectors $\begin{align*} g = -6i + 9j -7k\end{align*}$ and $\begin{align*}y = -24i + 36j -28k\end{align*}$ What is the cross product between g and y?
      ::矢量 g6i+9j-7k 和y24i+36j-28k g与y之间的交叉产品是什么?
  播放段落
  16. A boat is sailing on a bearing of 89° east of north at 564 feet per min. A tail wind is adding to the plane's velocity and blowing 78° west of north at 25 feet per min. Determine the actual speed of the plane in mph.
      ::一艘船只在北纬89度以东,每分钟564英尺处航行,尾风增加飞机速度,向北飞行78度,每分钟25英尺。
  播放段落
  17. A plane is flying on a bearing of 77° east of south at 606 mph. A tail wind is adding to the plane's velocity and blowing 33° west of south at 80 mph. Determine the direction of the plane.
      ::一架飞机在南纬77度以东606英里处飞行,尾风增加飞机速度,在80英里处向南33度以西吹,确定飞机方向。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。