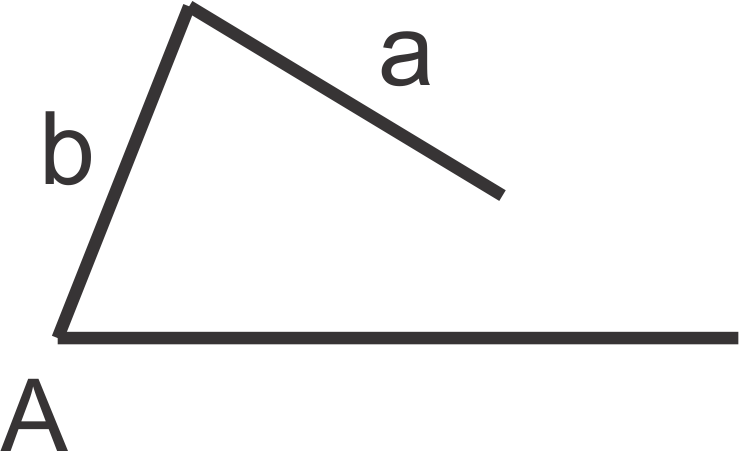13.13 不明的个案 -- -- 特别服务协定
章节大纲
-
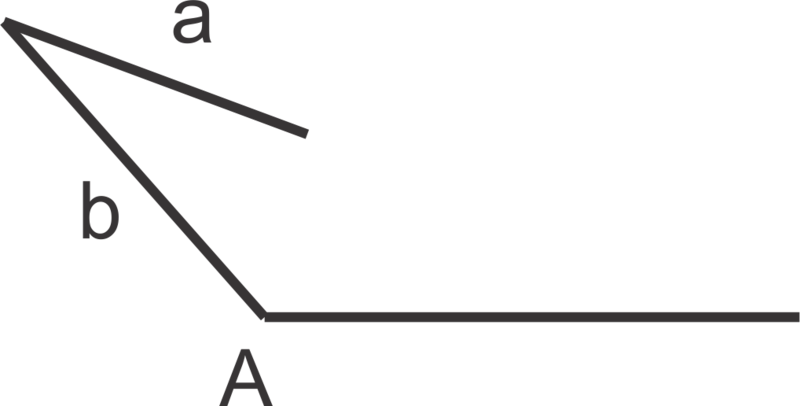
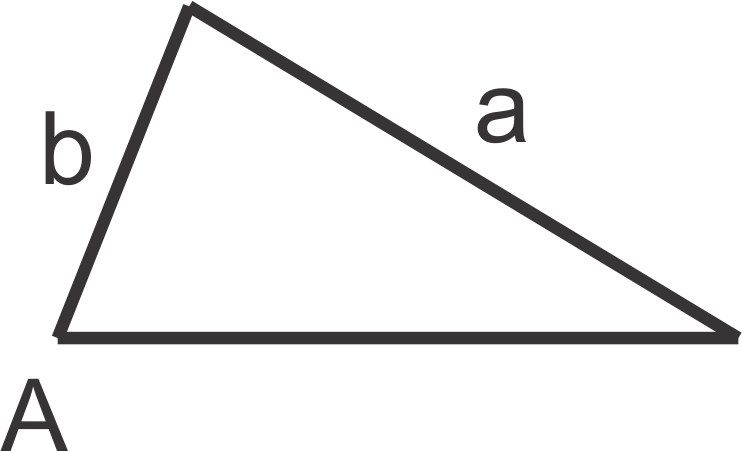
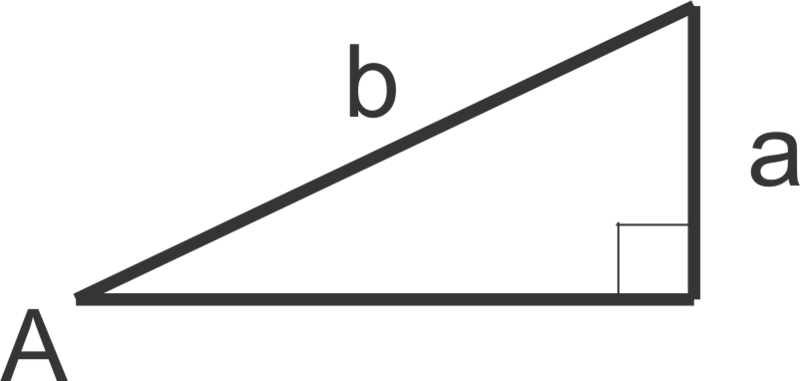
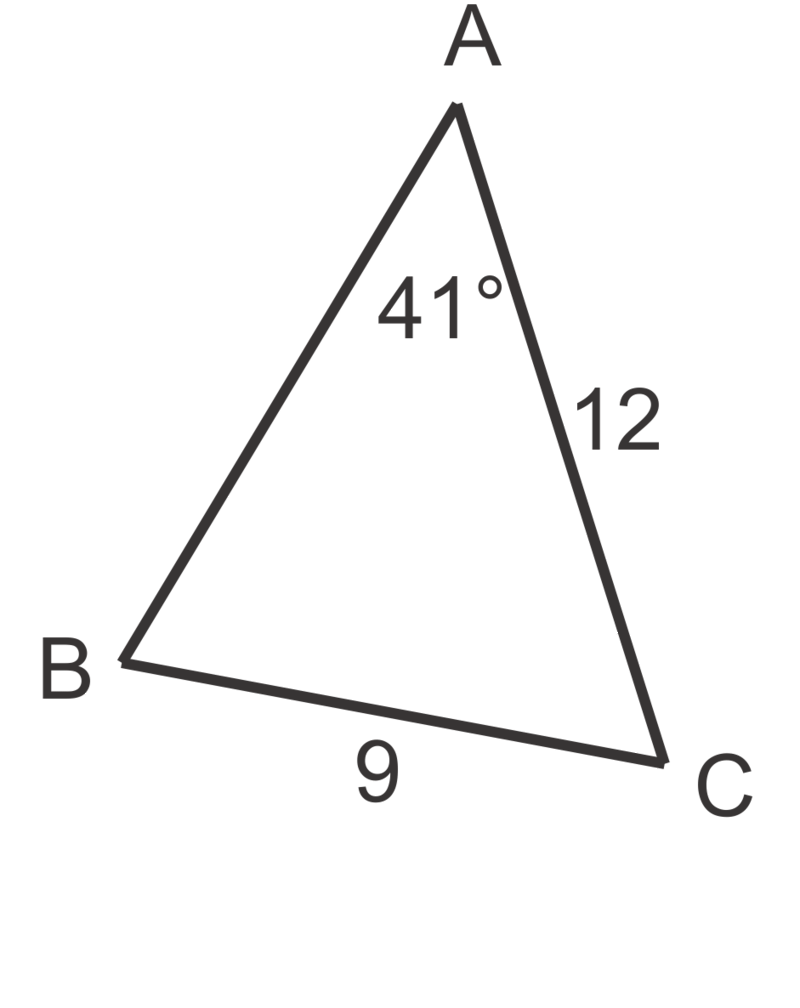
A triangle has two sides of lengths 2 (a) and 5 (b). The non-included angle (B) of the triangle measures . What are possible measures for the two other angles and the remaining side?
::三角形的长度为2(a)和5(b)的两面。 三角形中未包含角(B)的度量为45。 对于其他两个角度和另一面,可以采取哪些措施?SSA
::特别特别服务Recall that the sine ratios for an angle and its supplement will always be equal. In other words, . In Geometry you learned that two triangles could not be proven congruent using SSA and you investigated cases in which there could be two triangles. In the first problem below, we will explore how the can be used to find two possible triangles when given two side lengths of a triangle and a non-included angle.
::回顾角度的正弦比及其补充值总是相等。 换句话说, sinsin( 180) 。 在几何学中, 你发现使用 SSA 无法证明两个三角形是相同的, 你调查了可能有两个三角形的案件。 在下面第一个问题中, 我们将会探索当给三角形和未包含角两个侧长时, 如何使用这两个三角形来找到两个可能的三角形 。Given with , , and , let's solve for the other angle and side measures.
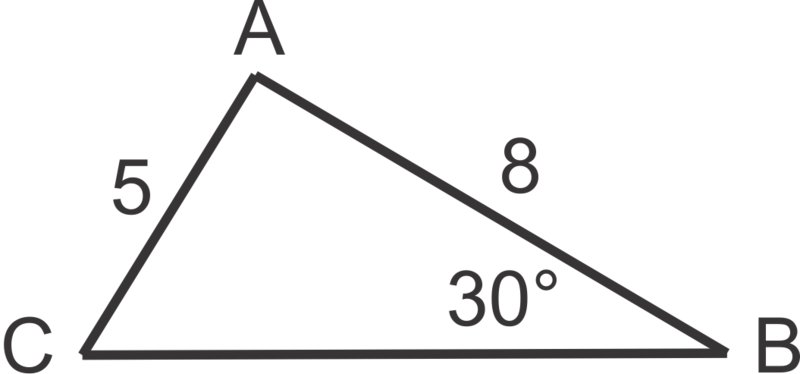
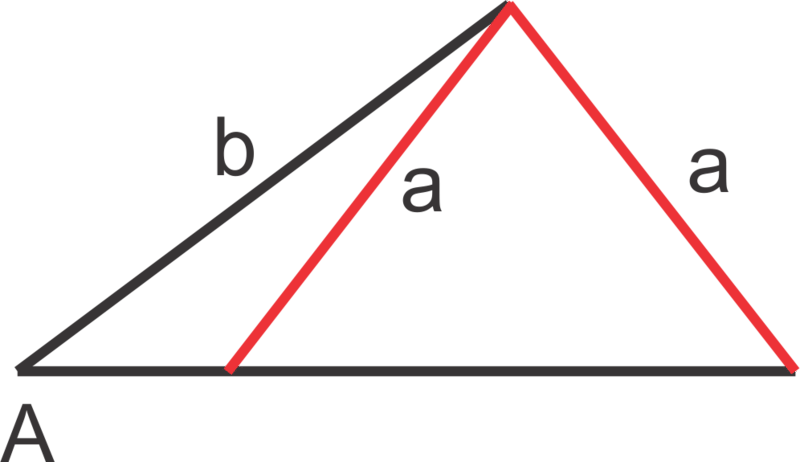
::鉴于 ABC 与 mA=30, a=5, b=8, 让我们解决其他角度和侧边措施 。First, let’s make a diagram to show the relationship between the given sides and angles. Then we can set up a proportion to solve for angle :
::首先,让我们绘制一个图表来显示给定的边和角之间的关系。 然后我们可以设定一个比例来解答角C:
::-=YTET -伊甸园字幕组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=-From here we can find , since the three angles must add up to . We can also find the third side using another Law of Sines ratio:
::我们从这里可以找到 mA=96.9, 因为这三个角度必须加到180。
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:Putting these measures in the triangle, we get:
::把这些措施放在三角形上,我们得到:But, we know that so when we solved for we only got one of the two possible angles. The other angle will be . Next we need to determine the measure of angle for and the length of the third side in this second possible triangle. The sum of the three angles must still be , so . Now set up a proportion to solve for the third side just as before:
::但是,我们知道,当我们为C解决了问题时,我们只有两个可能的角中的一个。另一个角将是 18053.1126.9。接下来我们需要确定这个第二个可能的三角形的A角和第三面的长度。这三个角的总和必须仍然是 180, 所以 mA=23.1。 现在为第三面设定一个比例, 和以前一样 :
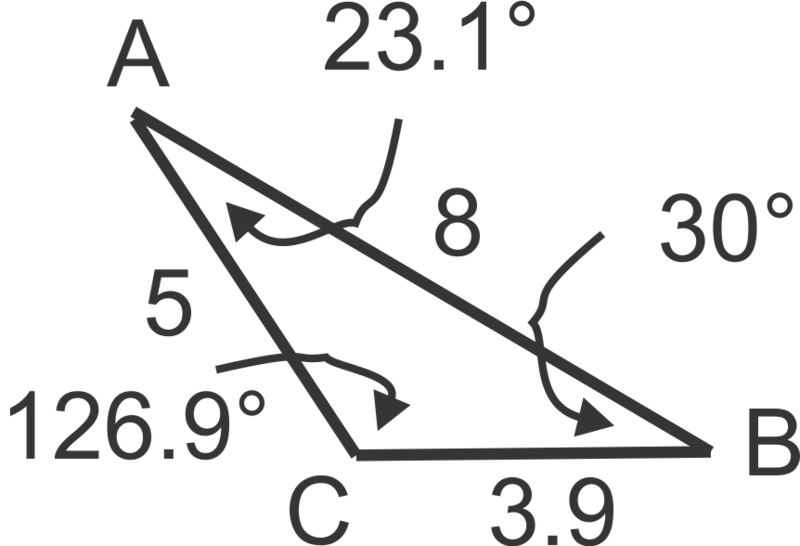
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:The second triangle would look like this:
::第二个三角形看起来是这样的:In this instance there were two possible triangles.
::在这种情况下,可能有两个三角形。Now, given with , and , let's solve for the other angle and side measures.
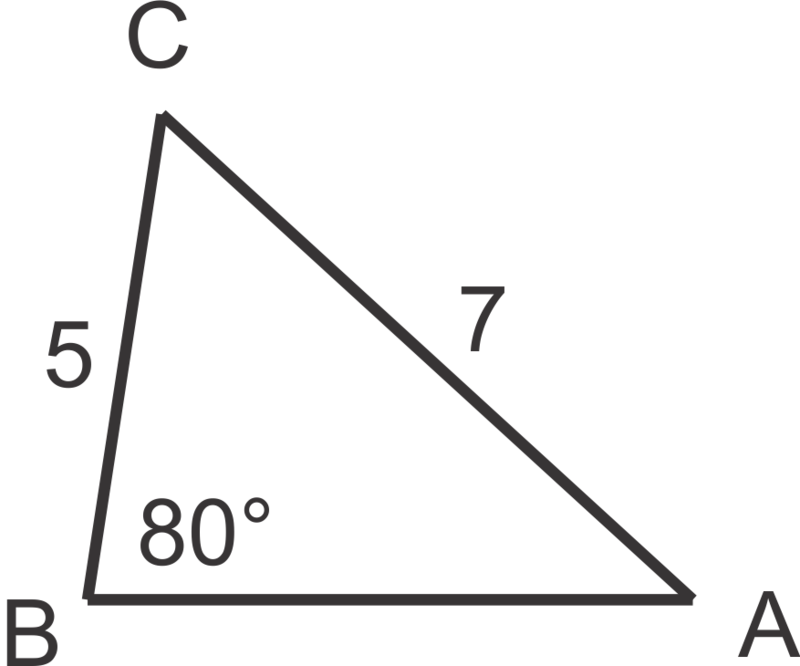
::现在, 给 QB=80, a=5 和 b= 7 的 ABC 加上 mB=80, a=5 和 b= 7 , 我们为其它角度和侧边度量度解决 。Again we will start with a diagram and use the law of sines proportion to find a second angle measure in the triangle.
::我们将从图表开始,使用正弦比例法来在三角形中找到第二个角度量。
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:Now find the third angle, and solve for the third side:
::现在找到第三个角度,1808044755.3, 并解决第三边:
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:Because we used the inverse sine function to determine the measure of angle , the angle could be the supplement of or so we need to check for a second triangle. If we let and then attempt to find the third angle, we will find that the sum of the two angles we have is greater than and thus no triangle can be formed.
::因为我们使用反正正弦函数来确定角度 A 的度量, 角度可能是44.7 或135.3 的补充值, 所以我们需要检查第二个三角 。 如果我们让 mA=135.3 然后试图找到第三个角度, 我们就会发现我们拥有的两个角度的总和大于 180, 因此无法形成三角 。
::mA+mB+mC=18013580mC=180215.3C>180This problem shows that two triangles are not always possible. Note that if the given angle is obtuse, there will only be one possible triangle for this reason.
::这个问题表明两个三角并非总有可能。 请注意, 如果给定角度是隐蔽的, 为此原因只可能有一个三角 。In both problems, we simply tested to see if there would be a second triangle. There are, however, guidelines to follow to determine when a second triangle exists and when it does not. The “check and see” method always works and therefore it is not necessary to memorize the following table. It is interesting, however, to see to pictures and make the connection between the inequalities and what if any triangle can be formed.
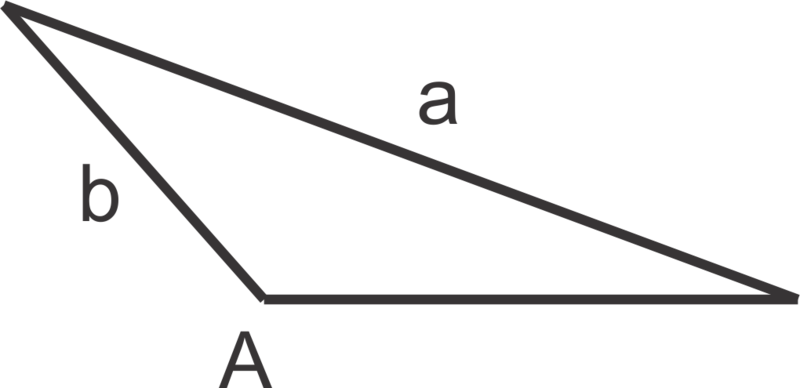
::在这两个问题中,我们只是试探是否会出现第二个三角。然而,在确定第二个三角何时存在和何时不存在时,需要遵循一些准则。 “检查和观察”方法总是有效的,因此没有必要背念下一张表格。然而,令人感兴趣的是,看到图象,将不平等与任何三角之间形成何种联系。First, consider when is obtuse:
::首先,考虑A是隐蔽的:If , then one triangle can be formed.
::如果 a>b,则可以组成一个三角形。If , then no triangle can be formed.
::如果 ab, 则无法形成三角形 。Now, consider the possible scenarios when is acute.
::现在,考虑一下A急性时可能出现的情况。If , the one triangle can be formed.
::如果 a>b , 一个三角形可以组成 。For the following cases, where , keep in mind that we would be using the proportion:
::对于以下情况,如果a <b,应铭记我们将使用该比例:and that
::Aa=sin_Bb 和sin_B=bsin_Aa 和sin_B=bsin_Aa 和sin_B=bsin_Aa 和sin_B=bsin_AaIf , no triangle can be formed because .
::如果 bsinA>a, 因为 B>1 无法形成三角形 。If , one right triangle can be formed because .
::如果 bsinA=a, 一个右三角形可以组成, 因为 sinB=1 。If (and ), two triangles can be formed because .
::如果 bsinA<a (和 a<b) , 则会因 sinB < 1 而形成两个三角形 。Finally, given with , and , let's use the rules to determine how many, if any, triangles can be formed and then solve the possible triangle(s).
::最后,根据 A=42, b=10 和 a=8 的 ABC 和 mA=42, b=10 和 a=8, 我们使用规则来确定可以组成多少三角形, 如果有的话, 然后解决可能的三角形 。In this case, is acute and , so we need to look at the value of . Since , there will be two triangles. To solve for these triangles, use the Law of Sines extended proportion instead of making a diagram. Plugging in what we know, we have:
::在此情况下, A是急性和 a<b, 所以我们需要查看 bsina 的值。 由于 bsinA = 10sin426. 69<a, 将有两个三角形。 要解决这些三角形, 请使用Sines 法则扩展比例, 而不是绘制图表 。 插进我们所知道的情况, 我们发现 :
::-42=8=sin=Bb=sin=C10 -Take the first and last ratios to solve a proportion to find the measure of angle .
::使用第一个和最后一个比率来解析比例以找到角度 A 的度量 。
::-=YTET -伊甸园字幕组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=-So, the or and or respectively.
::因此,分别是mC56.8或123.2和14.8BB81.2或14.8。Solve for the measure of side in each triangle:
::每个三角形的侧边 b 的度量 :
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:Putting it all together, we have:
::将所有这一切结合在一起,我们有:Triangle 1:
::三角1: mA42, mB81.2, mC=56.8a=8,b11.8,c=10Triangle 2:
::三角形2: mA42,mB14.8,mC=123.2a=8,b3.1,c=10Examples
::实例Example 1
::例1Earlier, you were asked to find the other two angles and the remaining side given that a triangle has two sides of lengths 2 (a) and 5 (b) and the non-included angle (B) measures .
::早些时候,有人要求你找到另外两个角度和另一边,因为三角形的长度为2(a)和5(b)两面,而未包括角(B)的度量为45{____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
::5=sinA2sinA=2sin455A=sin_12sin45516.44Now find the third angle, and solve for the third side:
::现在找到第三个角度, 1804516.4118.6,
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:Use the given side lengths and angle measure to determine whether zero, one or two triangles exists.
::使用给定的侧边长度和角度量来确定是否存在零、一个或两个三角形。Example 2
::例2.
::mA=100,a=3,b=4。Since is obtused and , no triangle can be formed.
::由于A被蒙蔽和 ab, 无法形成三角形 。Example 3
::例3.
::mA=50,a=8,b=10。Since is acute, and , two triangles can be formed.
::由于A是急性、a<b和bsinA>a,可以形成两个三角形。Example 4
::例4.
::mA=72,a=7,b=6。Since is acute and , there is one possible triangle.
::由于A是急性和 a>b,所以可能有一个三角形。Solve the following triangles.
::解决以下三角形。Example 5
::例5There will be two triangles in this case because is acute, and .
::在此情况下将有两个三角形, 因为 A是急性的, a <b > 和 bsinA <a > 。Using the extended proportion: , we get:
::使用扩展比例: sin256=sinB8=sinCc,我们得到:
::@ @ @ @ @ @ @ @ @%34.3 @_orm @B_145.7 @m @C_120.7 @m_C_9.3 @c_12.2c}c%2.3Example 6
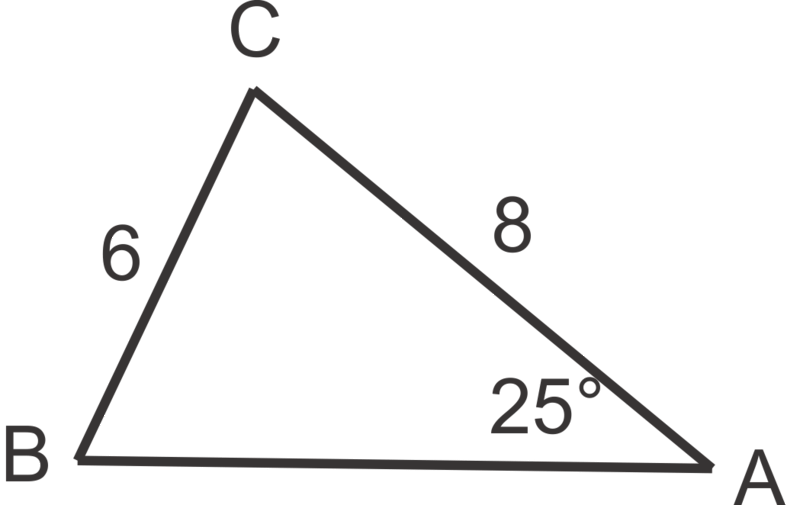
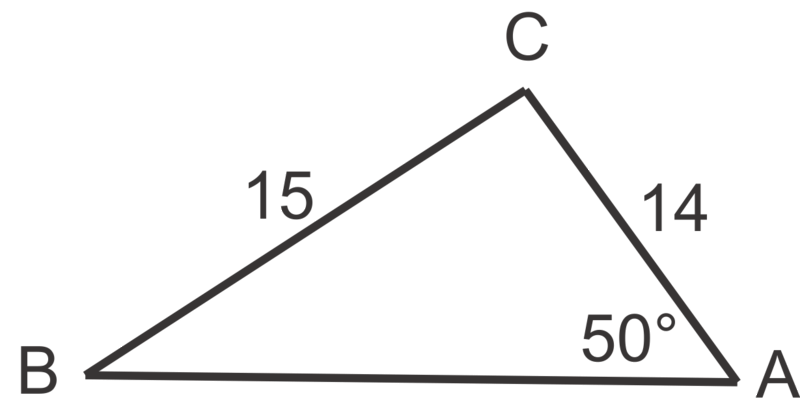
::例6Using the extended proportion: , we get:
::使用扩展比例: sin5015=sinB14=sinCc,我们得到:
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}...Example 7
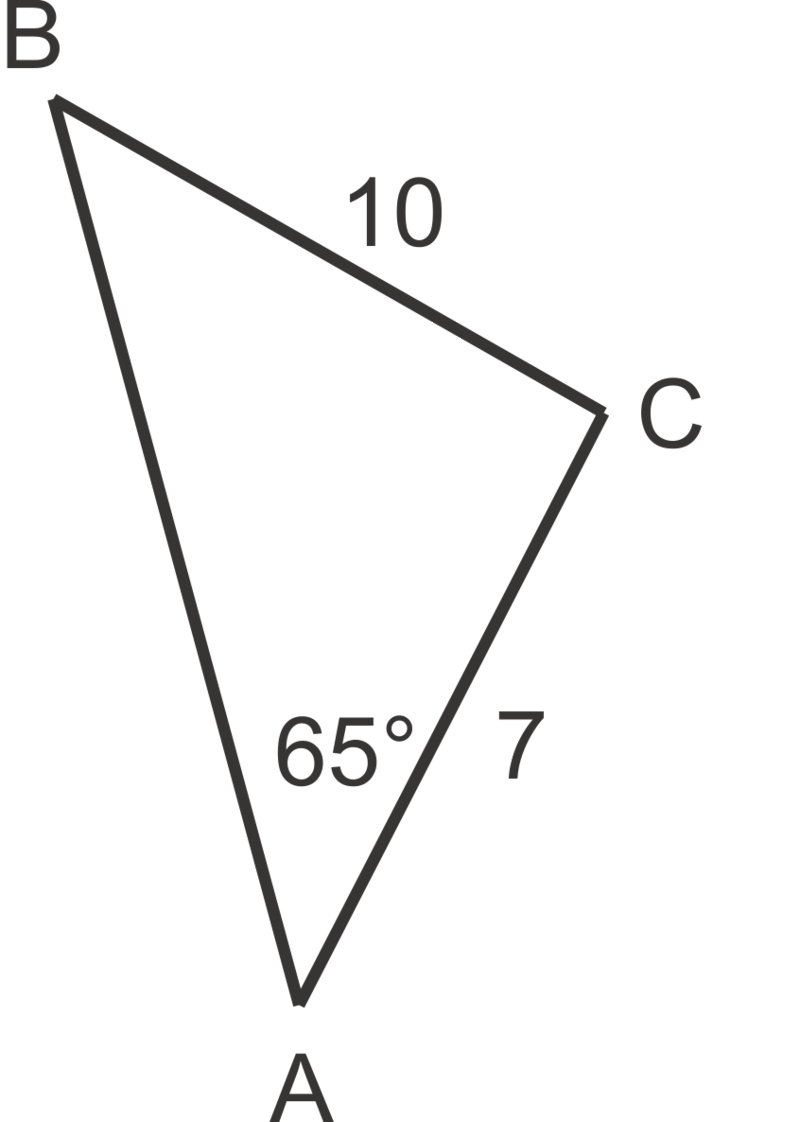
::例7Given , and , find .
::鉴于mA=30,a=80和b=150,找到mC。In this instance is acute, and so two triangles can be formed. So, once we find the two possible measures of angle , we will find the two possible measures of angle . First find :
::在此例中, A是急性的, a < b 和 bsina < a 使两个三角形能够形成。 因此, 一旦找到角 B 的两种可能的度量, 我们就会找到角 C 的两种可能的度量 。 首先找到 mB :
::=150sin_B=150sin_B=150sin_30_B_80_B_69.6_,110.4_Now that we have , use the triangle sum to find .
::现在我们有了B,用三角形的金额 找到mC80.4,39.9。Review
::回顾For problems 1-5, use the rules to determine if there will be one, two or no possible triangle with the given measurements.
::对于问题1至5,使用规则来确定是否与给定的测量结果有1、2或不可能的三角形。-
::mA=65,a=10,b=11 -
::mA=25,a=8,b=15 -
::mA=100a=6,b=4 -
::mA=75,a=25,b=30 -
::mA=48a=41,b=50
Solve the following triangles, if possible. If there is a second possible triangle, solve it as well.
::如果可能的话, 解决以下三角形 。 如果有第二个可能的三角形, 也解决它 。Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -