13.14 三角地区

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三角三角区域区域

  Collapse Expand

  三角三角区域区域

  播放段落

  Toby draws a triangle that has two side lengths of 8 inches and 5 inches. He measures the included angle with a protractor and gets $\begin{array}{r}{75}^{\circ }\end{array}$ . What is the area of this triangle?
  ::托比绘制一个边长为8英寸和5英寸的三角形。 他用一个减速器测量包含的角度, 并获得 75 。 这个三角形的面积是什么 ?

  播放段落

  Area of a Triangle
  ::三角三角区域区域

  播放段落

  Recall the non right triangle for which we derived the law of sine.
  ::回想一下非右三角,我们由此推导出正弦定律。

  播放段落

  We are most familiar with the area formula: $\begin{array}{r}A=\frac{1}{2}bh\end{array}$ where the base, $\begin{array}{r}b\end{array}$ , is the side length which is perpendicular to the altitude. If we consider angle $\begin{array}{r}C\end{array}$ in the diagram, we can write the following trigonometric expression for the altitude of the triangle, $\begin{array}{r}h\end{array}$ :
  ::我们最熟悉区域公式:A=12bh,其基数,b,是与高度垂直的侧长。如果我们在图表中考虑角度C,我们可以写下三角形高度的三角表达式,h:

  播放段落

  $$\begin{array}{rl}\sin C& =\frac{h}{b}\\ b\sin C& =h\end{array}$$

  
  ::C=hbbsin\\\\\\h\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  

  播放段落

  No we can replace $\begin{array}{r}h\end{array}$ in the formula with $\begin{array}{r}b\sin C\end{array}$ and the side perpendicular to $\begin{array}{r}h\end{array}$ is the base, $\begin{array}{r}a\end{array}$ . Our new area formula is thus:
  ::无法用 bsinC 替换公式中的 h , 而与 h 垂直的侧面是基底, a。 因此,我们的新区域公式是:

  播放段落

  $$\begin{array}{r}A=\frac{1}{2}ab\sin C.\end{array}$$

  
  ::A=12ab sin_C. 12ab sin_C. 12ab sin_C. 12ab sin_C. 12ab sin_C. 12ab sin_C. 12ab sin_C. 12ab sin_C.

  播放段落

  It is important to note that $\begin{array}{r}C\end{array}$ is the angle between sides $\begin{array}{r}a\end{array}$ and $\begin{array}{r}b\end{array}$ and that any two sides and the included angle can be used in the formula.
  ::必须指出,C是a方和b方之间的角,在公式中可以使用任何两方和包括的角。

  播放段落

  Let's find the area of the following triangles.
  ::让我们找到以下三角形的面积。

  1. 

  播放段落

  We are given two sides and the included angle so let $\begin{array}{r}a=6\end{array}$ , $\begin{array}{r}b=9\end{array}$ and $\begin{array}{r}C={62}^{\circ }\end{array}$ . Now we can use the formula to find the area of the triangle:
  ::我们得到两面和包括的角度,所以让我们用 a=6, b=9 和 C=62\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  $$\begin{array}{r}A=\frac{1}{2}(6)(9)\sin ({62}^{\circ })\approx 23.8squareunits\end{array}$$

  
  ::A=12(6)(9)sin(62)23.8平方单位

  2. 

  播放段落

  In this triangle we do not have two sides and the included angle. We must first find another side length using the . We can find the third angle using the triangle sum: $\begin{array}{r}{180}^{\circ }-{51}^{\circ }-{41}^{\circ }={88}^{\circ }\end{array}$ . Use the Law of Sines to find the side length opposite $\begin{array}{r}{41}^{\circ }\end{array}$ :
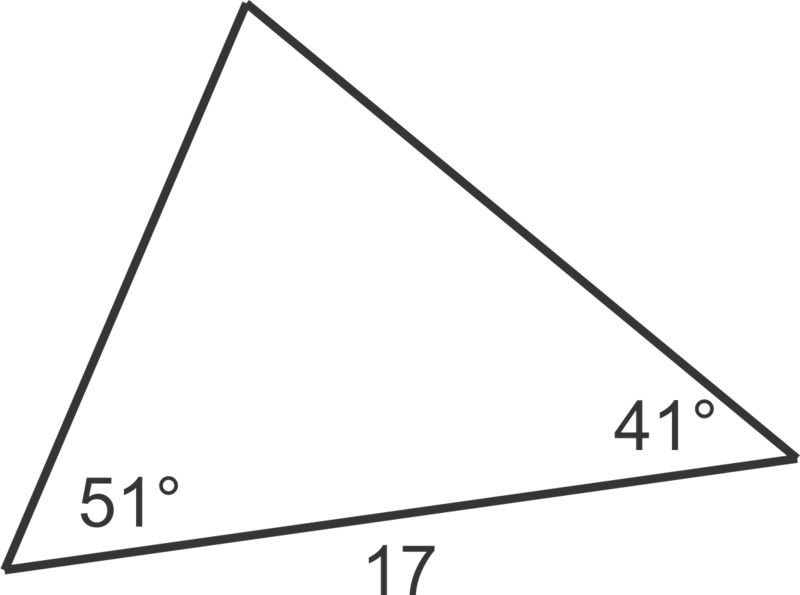
  ::在此三角形中, 我们没有两边和包含角度。 我们必须首先使用此边找到另一边长度 。 我们可以使用三角形总和, 找到第三个角度 : 180514188\\\\\\\\。 使用辛那法则找到对面41\\\\\\\\\\\\\\\\\的侧长度 :

  播放段落

  $$\begin{array}{rl}\frac{\sin {88}^{\circ }}{17}& =\frac{\sin {41}^{\circ }}{x}\\ x& =\frac{17\sin {41}^{\circ }}{\sin {88}^{\circ }}\approx 11.2\end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么?

  3. 

  播放段落

  We now have two sides and the included angle and can use the area formula:
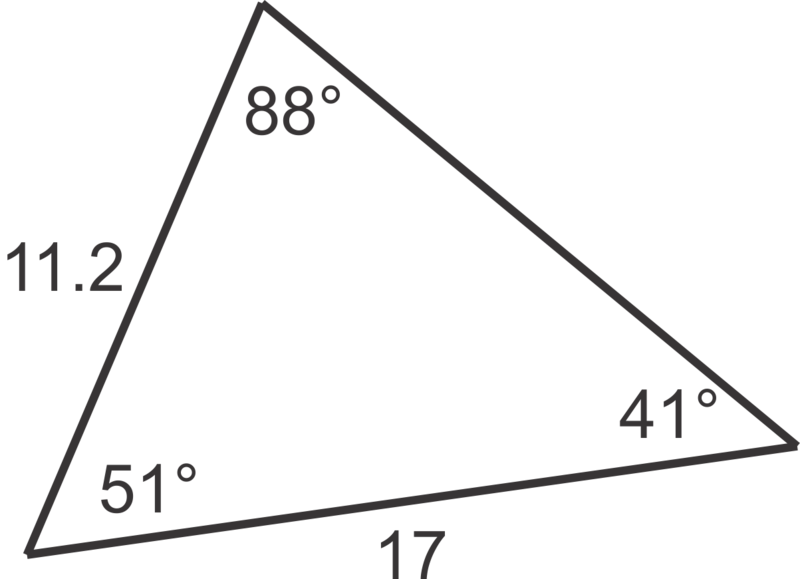
  ::我们现在有两面和包括的角度,可以使用面积公式:

  播放段落

  $$\begin{array}{r}A=\frac{1}{2}(11.2)(17)\sin ({51}^{\circ })\approx 74squareunits\end{array}$$

  
  ::A=12(11.2)(17)sin(51)(74平方单位)

  播放段落

  Finally, given $\begin{array}{r}c=25cm\end{array}$ , $\begin{array}{r}a=31cm\end{array}$ and $\begin{array}{r}B={78}^{\circ }\end{array}$ , find the area of $\begin{array}{r}\mathrm{\Delta }ABC\end{array}$ .
  ::最后,如果有c=25厘米、a=31厘米和B=78厘米,请找到ABC的区域。

  播放段落

  Here we are given two sides and the included angle. We can adjust the formula to represent the sides and angle we are given: $\begin{array}{r}A=\frac{1}{2}ac\sin B\end{array}$ . It really doesn’t matter which “letters” are in the formula as long as they represent two sides and the included angle (the angle between the two sides.) Now put in our values to find the area: $\begin{array}{r}A=\frac{1}{2}(31)(25)\sin ({78}^{\circ })\approx 379c{m}^2\end{array}$ .
  ::这里给出了两面和包含角度。 我们可以调整公式以代表我们给出的边和角度: A=12ac sinB。 只要“ 字母” 代表了两面和包含角度( 双方的角度) , 公式中的“ 字母” 在公式中其实并不重要 。 ) 现在, 在我们的数值中放入我们的数值以找到这个区域 : A=12( 31) (25)sin( 78)\\\\\\\_379 cm2。 A=12( 271)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find  the area of the triangle that has two side lengths of 8 inches and 5 inches and an included angle of  $\begin{array}{r}{75}^{\circ }\end{array}$ .
  ::早些时候,有人要求你找到三角形的面积,两侧长度为8英寸5英寸,其中角为75英寸。

  播放段落

  We are given two sides and the included angle so let $\begin{array}{r}a=8\end{array}$ , $\begin{array}{r}b=5\end{array}$ and $\begin{array}{r}C={75}^{\circ }\end{array}$ . Now we can use the formula to find the area of the triangle:
  ::我们得到两面和包括的角度,所以让我们 a=8, b=5 和 C=75\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  $$\begin{array}{r}A=\frac{1}{2}(8)(5)\sin ({75}^{\circ })\approx 19.4squareinches\end{array}$$

  
  ::A=12(8)(5)sin(75)19.4平方英寸

  播放段落

  Find the area of each of the triangles below. Round answers to the nearest square unit.
  ::查找下面每个三角形的面积。 圆对最近的平方单位的答案 。

  播放段落

  Example 2
  ::例2

  

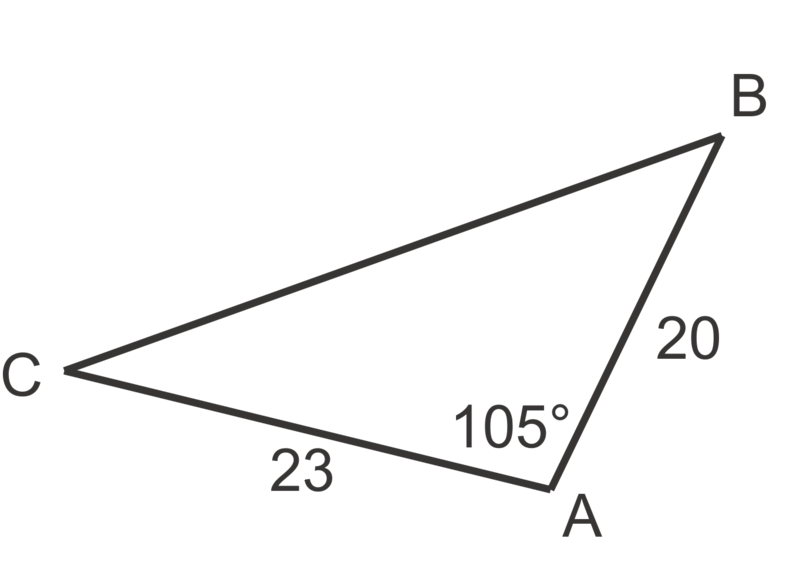
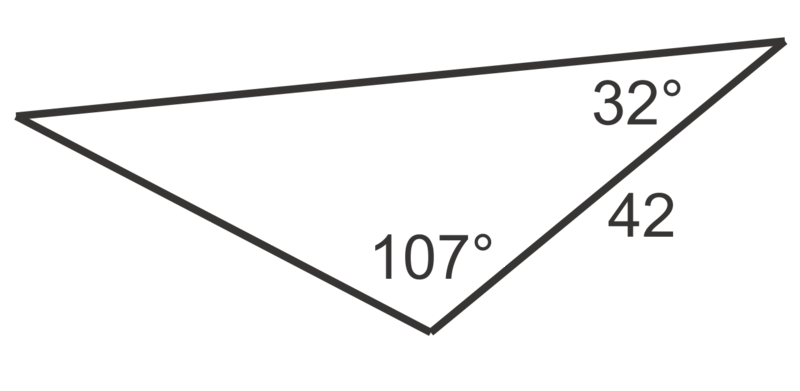
  播放段落

  Two sides and the included angle are given so $\begin{array}{r}A=\frac{1}{2}(20)(23)\sin {105}^{\circ }\approx 222squnits\end{array}$ .
  ::A=12(20)(23)sin105222平方米单位。

  播放段落

  Example 3
  ::例3

  

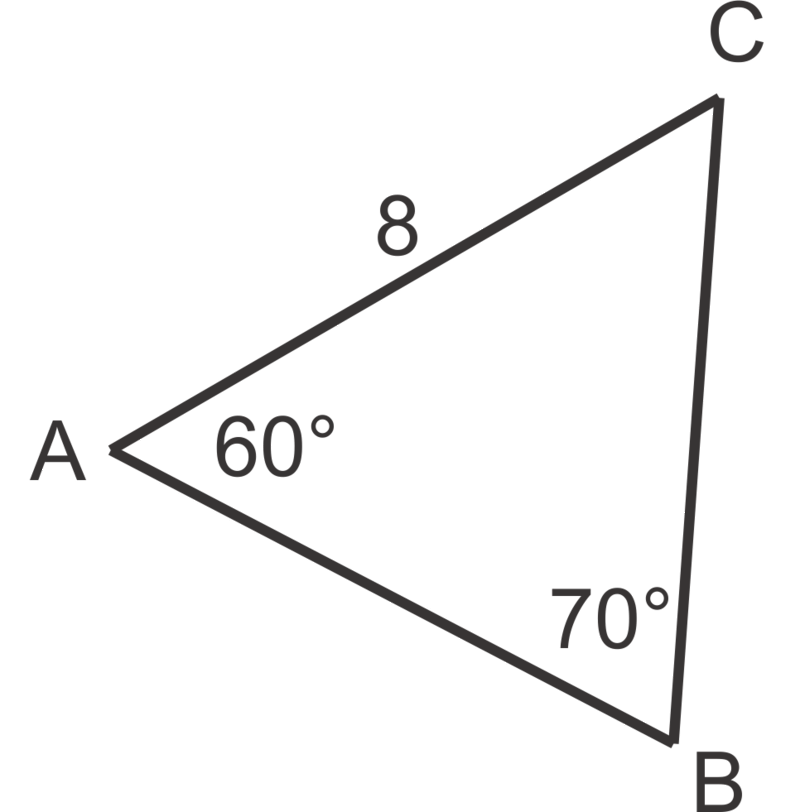
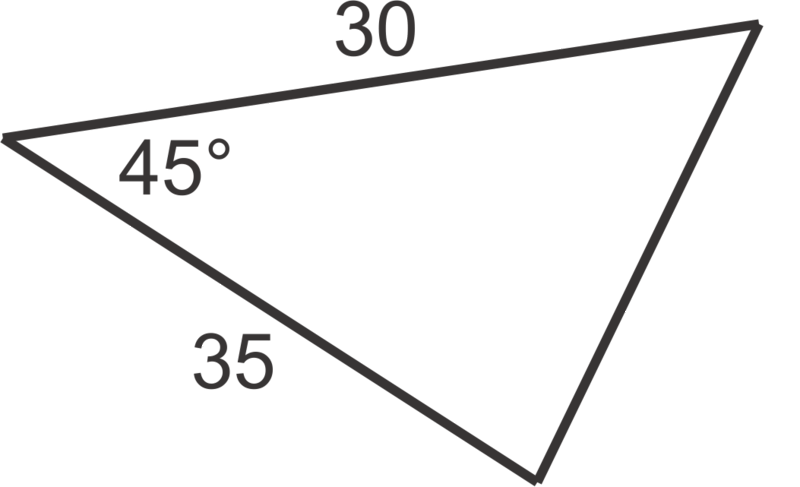
  播放段落

  Find side $\begin{array}{r}a\end{array}$ first: $\begin{array}{r}\frac{\sin {70}^{\circ }}{8}=\frac{\sin {60}^{\circ }}{a}\end{array}$ , so $\begin{array}{r}a=\frac{8\sin {60}^{\circ }}{\sin {70}^{\circ }}\approx 7.4\end{array}$ . Next find $\begin{array}{r}m\mathrm{\angle }C={180}^{\circ }-{60}^{\circ }-{70}^{\circ }={50}^{\circ }\end{array}$ .
  ::找到第一面: sin@708=sin60a, 所以a=8sin6060707. 4。 下一个找到 mC=180607050 。

  播放段落

  Using the area formula, $\begin{array}{r}A=\frac{1}{2}(7.4)(8)\sin {50}^{\circ }\approx 22.7squnits\end{array}$ .
  ::使用区域公式,A=12(7.4)(8)sin5022.7平方米单位。

  播放段落

  Example 4
  ::例4

  

  播放段落

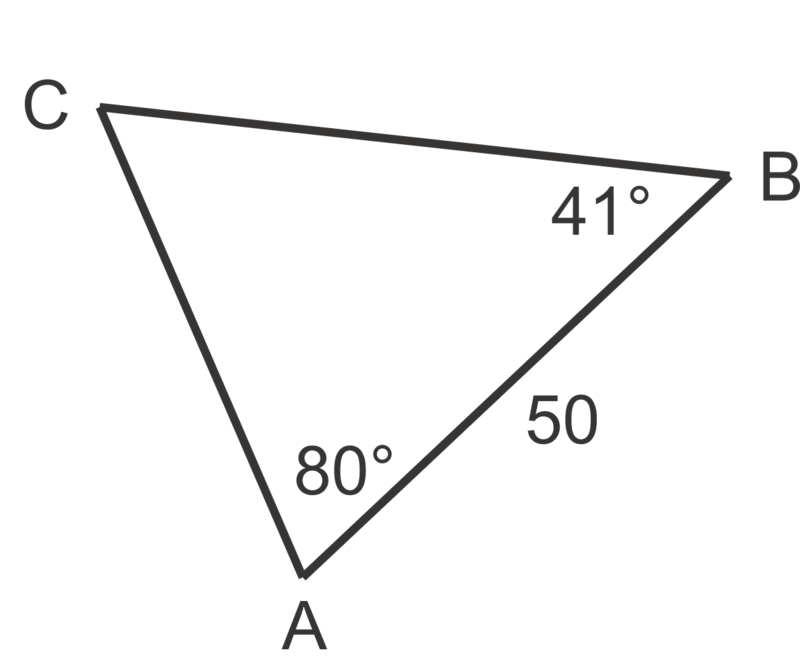
  Find $\begin{array}{r}m\mathrm{\angle }C={180}^{\circ }-{80}^{\circ }-{41}^{\circ }={59}^{\circ }\end{array}$ . Find a second side: $\begin{array}{r}\frac{\sin {59}^{\circ }}{50}=\frac{\sin {80}^{\circ }}{a}\end{array}$ , so $\begin{array}{r}a=\frac{50\sin {80}^{\circ }}{\sin {59}^{\circ }}\approx 57.4\end{array}$ .
  ::找到 mC = 180 80 41 59 。 找到第二面: sin 59 50 80 a, 所以 a= 50 sin80 59 57.4 。

  播放段落

  Using the area formula, $\begin{array}{r}A=\frac{1}{2}(57.4)(50)\sin {41}^{\circ }\approx 941squnits\end{array}$ .
  ::使用区域公式,A=12(57.4)(50)sin41941 sq单位。

  播放段落

  Review
  ::回顾

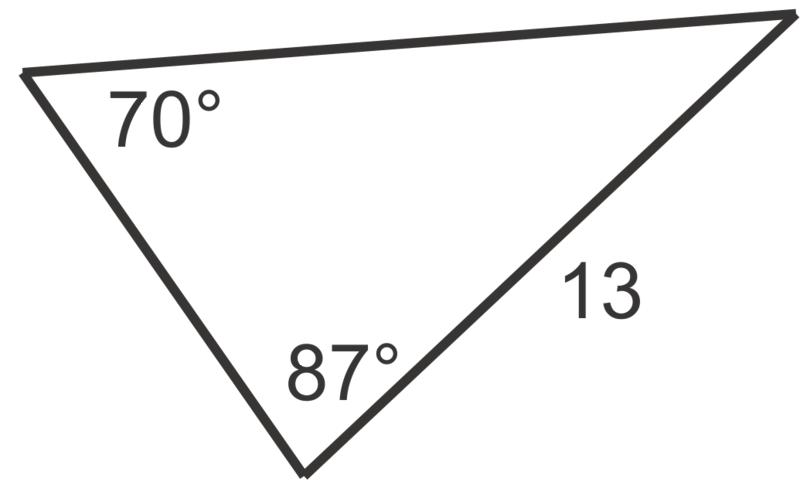
  播放段落

  Find the area of each of the triangles below. Round your answers to the nearest square unit.
  ::查找下面每个三角形的面积。 将您的答案绕到最近的平方单位 。

  1. 
  2. 
  3. 
  播放段落
  4. $\begin{array}{r}m\mathrm{\angle }A={71}^{\circ },b=15,c=19\end{array}$
     ::mA=71,b=15,c=19
  播放段落
  5. $\begin{array}{r}m\mathrm{\angle }C={120}^{\circ },b=22,a=16\end{array}$
     ::mC=120,b=22,a=16
  播放段落
  6. $\begin{array}{r}m\mathrm{\angle }B={60}^{\circ },a=18,c=12\end{array}$
     ::mB=60,a=18,c=12
  播放段落
  7. $\begin{array}{r}m\mathrm{\angle }A={28}^{\circ },m\mathrm{\angle }C={73}^{\circ },b=45\end{array}$
     ::mA=28\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
  播放段落
  8. $\begin{array}{r}m\mathrm{\angle }B={56}^{\circ },m\mathrm{\angle }C={81}^{\circ },c=33\end{array}$
     ::mB=56,mC=81,c=33
  播放段落
  9. $\begin{array}{r}m\mathrm{\angle }A={100}^{\circ },m\mathrm{\angle }B={30}^{\circ },a=100\end{array}$
     ::mA=100,mB=30,a=100
  播放段落
  10. The area of $\begin{array}{r}\mathrm{\Delta }ABC\end{array}$ is 66 square units. If two sides of the triangle are 11 and 21 units, what is the measure of the included angle? Is there more than one possible value? Explain.
      ::QABC 区域为 66 平方单位。 如果三角形的两边是 11 和 21 单位, 则包含角度的度量是多少? 是否有一个以上的值? 请解释 。
  播放段落
  11. A triangular garden is bounded on one side by a 20 ft long barn and a second side is bounded by a 25 ft long fence. If the barn and the fence meet at a $\begin{array}{r}{50}^{\circ }\end{array}$ angle, what is the area of the garden if the third side is the length of the segment between the ends of the fence and the barn?
      ::三角花园一面被20英尺长的谷仓捆绑,另一面被25英尺长的围栏捆绑,如果谷仓和栅栏在50英尺角相交,如果第三个边是栅栏两端与谷仓之间的部分长度,那么花园的面积是多少?
  播放段落
  12. A contractor is constructing a counter top in the shape of an equilateral triangle with side lengths 3 ft. If the countertop material costs $25 per square foot, how much will the countertop cost?
      ::承包商正在建造一个顶部柜台,其形状是侧长3英尺的等边三角形。 如果反顶材料每平方英尺花费25美元,反顶要花多少钱?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。