Course: 13.15 使用SAS的 " 共信法 " (以找到第三面)

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 使用SAS的Casine定律(寻找第三面)

Collapse Expand
使用SAS的Casine定律(寻找第三面)
Toby draws a triangle that has two side lengths of 8 inches and 5 inches. He measures the included angle with a protractor and gets $\begin{align*}75^\circ\end{align*}$ . What is the length of the third side?
::托比绘制一个三角形,其两侧长度为8英寸和5英寸。他用一个减速器测量包含的角度,然后获得75英寸。第三边的长度是多少?

Law of Cosines
::科士法

The Law of Cosines can be used to solve for the third side of a triangle when two sides and the included angle are known in a triangle. consider the non right triangle below in which we know $\begin{align*}a, b\end{align*}$ and $\begin{align*}C\end{align*}$ . We can draw an altitude from $\begin{align*}B\end{align*}$ to create two smaller right triangles as shown where $\begin{align*}x\end{align*}$ represents the length of the segment from $\begin{align*}C\end{align*}$ to the foot of the altitude and $\begin{align*}b-x\end{align*}$ represents the length of remainder of the side opposite angle $\begin{align*}B\end{align*}$ .
::当三角形中知道两边和包括角度时,Casines定律可用于三角形第三侧的解析。考虑以下非右三角形, 我们从B中绘制一个高度, 以创建两个较小的右三角形, 如 x 表示段的长度, 从 C 到高度的脚, b- x 表示侧角 B 的剩余长度。

Now we can use the to relate the lengths of the segments in each of the right triangles shown.
::现在我们可以使用它来连接显示的每个右三角形的区段长度。

Triangle 1: $\begin{align*}x^2+k^2=a^2\end{align*}$ or $\begin{align*}k^2=a^2-x^2\end{align*}$
::三角形1: x2+k2=a2或k2=a2-x2

Triangle 2: $\begin{align*}(b-x)^2+k^2=c^2\end{align*}$ or $\begin{align*}k^2=c^2-(b-x)^2\end{align*}$
::三角形 2: (b-x) 2+k2=c2 或 k2=c2 - (b-x)2

Since both equations are equal to $\begin{align*}k^2\end{align*}$ , we can set them equal to each other and simplify:
::由于两个方程式都等于k2, 我们可以把它们等同, 并简化:

$\begin{aligned} a^{2} - x^{2} & = c^{2} - (b - x)^{2} \\ a^{2} - x^{2} & = c^{2} - (b^{2} - 2 b x + x^{2}) \\ a^{2} - x^{2} & = c^{2} - b^{2} + 2 b x - x^{2} \\ a^{2} & = c^{2} - b^{2} + 2 b x \\ a^{2} + b^{2} - 2 b x & = c^{2} \end{aligned}$
$\begin{align*}a^2-x^2 &=c^2-(b-x)^2 \\ a^2-x^2 &=c^2-(b^2-2bx+x^2) \\ a^2-x^2 &=c^2-b^2+2bx-x^2 \\ a^2 &=c^2-b^2+2bx \\ a^2+b^2-2bx &=c^2\end{align*}$
::a2-x2=c2-(b-x)2-(b-x)2-a2-x2=c2-2-(b2-2bx+x2)-(b2-2bx+x2)-x2=c2-2-b2-x2x-x2a2=c2-2-b2+2bx2+b2-b2-2bx=c2

Recall that we know the values of $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ and the measure of angle $\begin{align*}C\end{align*}$ . We don’t know the measure of $\begin{align*}x\end{align*}$ . We can use the cosine ratio as show below to find an expression for $\begin{align*}x\end{align*}$ in terms of what we already know.
::回顾我们知道a和b的值以及角度C的度量。我们不知道x的度量。我们可以用下文显示的余弦比来找到x的表达方式, 即我们已经知道的。

$\begin{aligned} \cos C = \frac{x}{a} so x = a \cos C \end{aligned}$
$\begin{align*} \cos C=\frac{x}{a} \quad \text{so} \quad x=a \cos C\end{align*}$
::COsC = Xassox=acosC =xassox=acosC =xassox=acosC =xxxxxxxx=acos=acosC =xxxxxxxxx=acos=acos=C

Finally, we can replace $\begin{align*}x\end{align*}$ in the equation to get the Law of Cosines: $\begin{align*}a^2+b^2-2ab \cos C=c^2\end{align*}$
::最后,我们可以在方程中替换 x , 以获得科辛定律: a2+b2-2- 2abcosC=c2

Keep in mind that $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are the sides of angle $\begin{align*}C\end{align*}$ in the formula.
::铭记a和b是公式中角度C的两边。

Let's find $\begin{align*}c\end{align*}$ when $\begin{align*}m \angle C=80^\circ, a = 6\end{align*}$ and $\begin{align*}b = 12\end{align*}$ .
::让我们在 mC=80,a=6和b=12时找到c。

Replacing the variables in the formula with the given information and solve for $\begin{align*}c\end{align*}$ :
::以给定的信息替换公式中的变量,并解决 c:

$\begin{aligned} c^{2} & = 6^{2} + 12^{2} - 2 (6) (12) \cos 80^{\circ} \\ c^{2} & \approx 154.995 \\ c & \approx 12.4 \end{aligned}$
$\begin{align*}c^2 &=6^2+12^2-2(6)(12) \cos 80^\circ \\ c^2 & \approx 154.995 \\ c & \approx 12.4\end{align*}$
::c2=62+122-2(6)(12)cos80c2154.995c12.4

Now, let's find $\begin{align*}a\end{align*}$ , when $\begin{align*}m \angle A=43^\circ\end{align*}$ , $\begin{align*}b=16\end{align*}$ and $\begin{align*}c=22\end{align*}$ .
::现在,让我们找到一个, 当mA=43,b=16和c=22。

This time we are given the sides surrounding angle $\begin{align*}A\end{align*}$ and the measure of angle $\begin{align*}A\end{align*}$ . We can rewrite the formula as: $\begin{align*}a^2=c^2+b^2-2cb \cos A\end{align*}$ . Just remember that the length by itself on one side should be the side opposite the angle in the cosine ratio. Now we can plug in our values and solve for $\begin{align*}a\end{align*}$ .
::这一次,我们得到角A周围的侧面和角A的度量。我们可以将公式重写为: a2=c2+b2-2-2cbccosA。只需记住, 单面的长度应该是正对角的对面, 在余弦比例中。现在我们可以插入我们的值, 并解决一个值。

$\begin{aligned} a^{2} & = 16^{2} + 22^{2} - 2 (16) (22) \cos 43^{\circ} \\ a^{2} & \approx 225.127 \\ a & \approx 15 \end{aligned}$
$\begin{align*}a^2 &=16^2+22^2-2(16)(22) \cos 43^\circ \\ a^2 & \approx 225.127 \\ a & \approx 15 \end{align*}$
::a2=162+222-216(22)cos43a2225.127a}15

Finally, let's solve the following problem.
::最后,让我们解决以下问题。

Rae is making a triangular flower garden. One side is bounded by her porch and a second side is bounded by her fence. She plans to put in a stone border on the third side. If the length of the porch is 10 ft and the length of the fence is 15 ft and they meet at a $\begin{align*}100^\circ\end{align*}$ angle, how many feet of stone border does she need to create?
::Rae正在造一个三角花园,一面与她的门廊相邻,另一面与她的栅栏相邻,她计划把第三边的边框放在一块石头上。如果门廊的长度是10英尺,栅栏的长度是15英尺,他们以100英尺的角相会,那么她需要建造多少英尺的石头边框?

Let the two known side lengths be $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ and the angle between is $\begin{align*}C\end{align*}$ . Now we can use the formula to find $\begin{align*}c\end{align*}$ , the length of the third side.
::让已知的两个侧边长度为a和b, 中间的角度为C。现在我们可以使用公式来找到c, 即第三边的长度。

$\begin{aligned} c^{2} & = 10^{2} + 15^{2} - 2 (10) (15) \cos 100^{\circ} \\ c^{2} & \approx 377.094 \\ c & \approx 19.4 \end{aligned}$
$\begin{align*}c^2 &=10^2+15^2-2(10)(15) \cos 100^\circ \\ c^2 & \approx 377.094 \\ c & \approx 19.4\end{align*}$
::c2=102+152-2(10)(15cos100c2377.094c19.4)

So Rae will need to create a 19.4 ft stone border.
::所以雷伊需要建立一个19.4英尺的石头边界

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the length of the third side given a triangle that has two sides of length 5 inches and 8 inches and an included angle of $\begin{align*}75^\circ\end{align*}$ .
::早些时候,有人要求你找到第三边的长度, 给出一个三角形, 其两边的长度为5英寸8英寸, 包括角度为75英寸。

We are trying to find $\begin{align*}c\end{align*}$ . We are given $\begin{align*}m \angle C=75^\circ, a = 8\end{align*}$ and $\begin{align*}b = 5\end{align*}$ .
::我们试图找到c。我们得到了 mC=75,a=8和b=5。

Replacing the variables in the formula with the given information and solve for $\begin{align*}c\end{align*}$ :
::以给定的信息替换公式中的变量,并解决 c:

$\begin{aligned} c^{2} & = 8^{2} + 5^{2} - 2 (8) (5) \cos 75^{\circ} \\ c^{2} = 64 + 25 - 80 \cos 75^{\circ} \\ c^{2} = 89 - 80 (0.26) \\ c^{2} & \approx 68.2 \\ c & \approx 8.26 \end{aligned}$
$\begin{align*}c^2 &=8^2+5^2-2(8)(5) \cos 75^\circ \\ c^2=64 + 25 - 80 \cos 75^\circ \\ c^2=89 - 80(0.26)\\ c^2 & \approx 68.2 \\ c & \approx 8.26\end{align*}$
::c2=89-80(0.26)c2_68.2c_8.26

Therefore, the third side is approximately 8.26 inches long.
::因此,第三面大约长8.26英寸。

Example 2
::例2

Find $\begin{align*}c\end{align*}$ when $\begin{align*}m \angle C=75^\circ, a = 32\end{align*}$ and $\begin{align*}b = 40\end{align*}$ .
::在 mC=75,a=32和b=40时查找 c。

$\begin{aligned} c^{2} & = 32^{2} + 40^{2} - 2 (32) (40) \cos 75^{\circ} \\ c^{2} & \approx 1961.42 \\ c & \approx 44.3 \end{aligned}$
$\begin{align*}c^2 &=32^2+40^2-2(32)(40) \cos 75^\circ \\ c^2 & \approx 1961.42 \\ c & \approx 44.3\end{align*}$
::c2=322+402-2(32)(40cos75c21961.42c44.3)。

Example 3
::例3

Find $\begin{align*}b\end{align*}$ when $\begin{align*}m \angle B=120^\circ, a = 11\end{align*}$ and $\begin{align*}c =17\end{align*}$ .
::在 mB=120,a=11和c=17时查找b。

$\begin{aligned} b^{2} & = 11^{2} + 17^{2} - 2 (11) (17) \cos 120^{\circ} \\ b^{2} & \approx 597 \\ b & \approx 24.4 \end{aligned}$
$\begin{align*}b^2 &=11^2+17^2-2(11)(17) \cos 120^\circ \\ b^2 & \approx 597 \\ b & \approx 24.4\end{align*}$
::b2=112+172-2(11)(17cos120b2597b24.4)。

Example 4
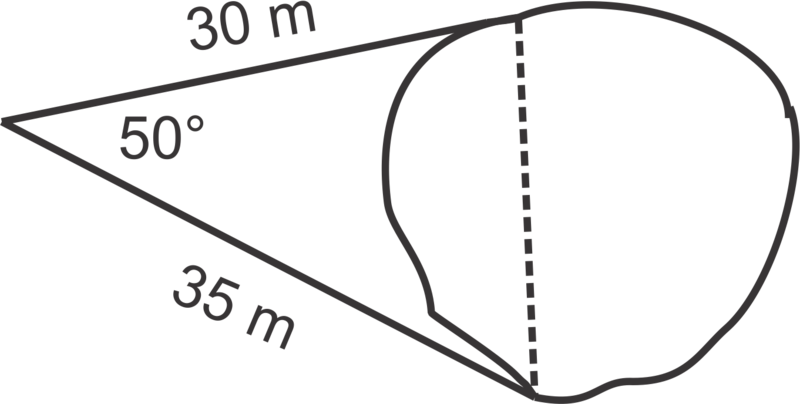
::例4

Dan likes to swim laps across a small lake near his home. He swims from a pier on the north side to a pier on the south side multiple times for a workout. One day he decided to determine the length of his swim. He determines the distances from each of the piers to a point on land and the angles between the piers from that point to be $\begin{align*}50^\circ\end{align*}$ . How many laps does Dan need to swim to cover 1000 meters?
::丹喜欢在离家附近的一个小湖上游圈。他从北边的码头游到南边的码头,多次锻炼。有一天他决定了游泳的长度。他决定了从每个码头到陆地的一个点的距离,以及从那个点到码头之间的角度是50。丹需要游泳多少圈才能覆盖1000米?

$\begin{aligned} c^{2} & = 30^{2} + 35^{2} - 2 (30) (35) \cos 50^{\circ} \\ c^{2} & \approx 775.146 \\ c & \approx 27.84 \end{aligned}$
$\begin{align*}c^2 &=30^2+35^2-2(30)(35) \cos 50^\circ \\ c^2 & \approx 775.146 \\ c & \approx 27.84\end{align*}$
::c2=302+352-2(30) (35)cos50c2775.146c27.84

Since each lap is 27.84 meters, Dan must swim $\begin{align*}\frac{1000}{27.84} \approx 36\end{align*}$ laps.
::因为每圈27.84米丹必须游泳100027.8436圈

Review
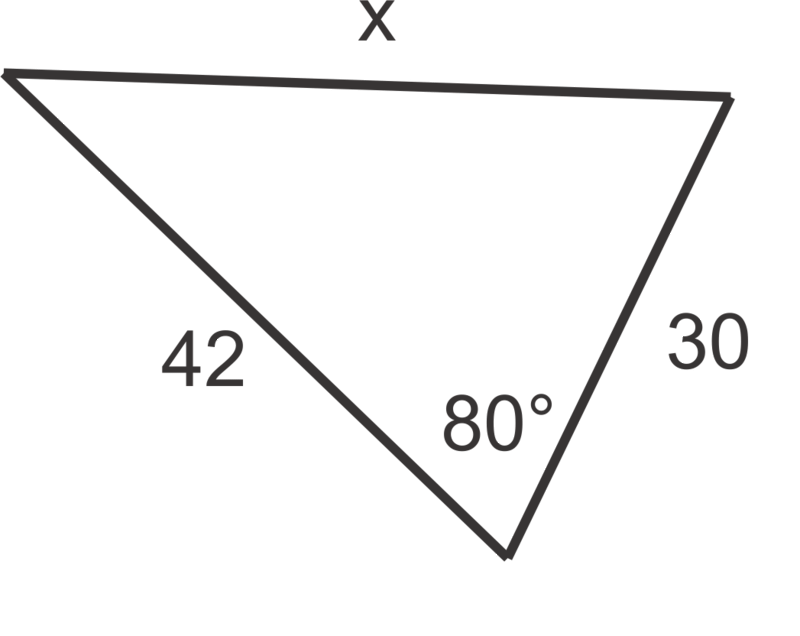
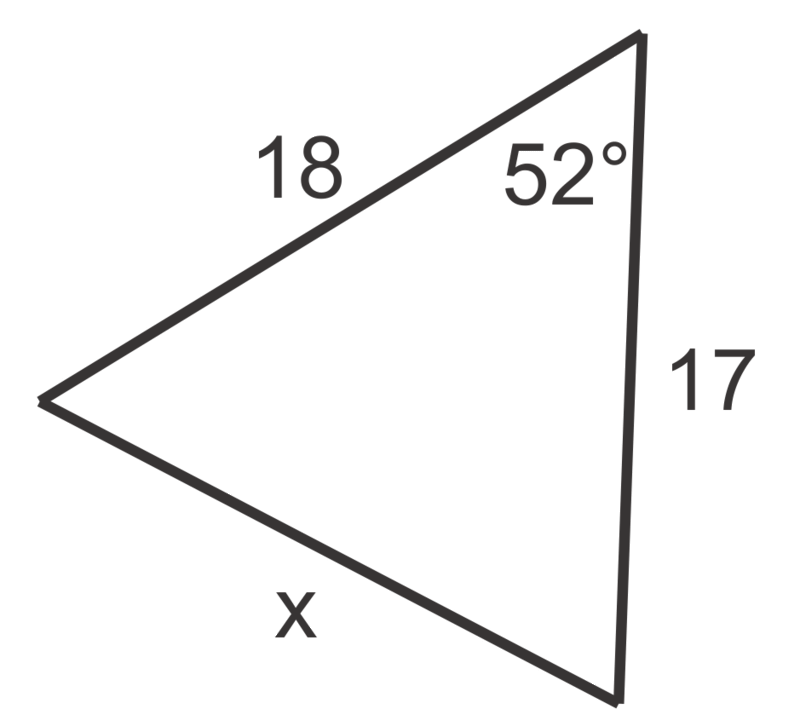
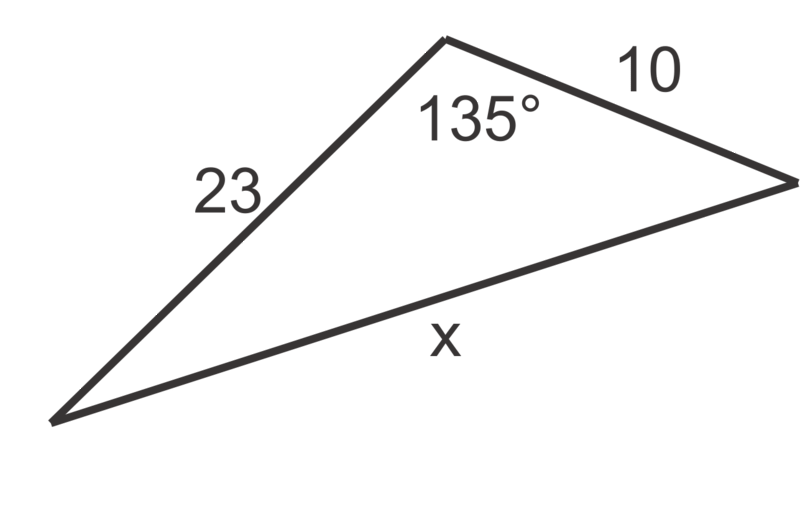
::回顾

Use the Law of Cosines to find the value of $\begin{align*}x\end{align*}$ , to the nearest tenth, in problems 1 through 6.
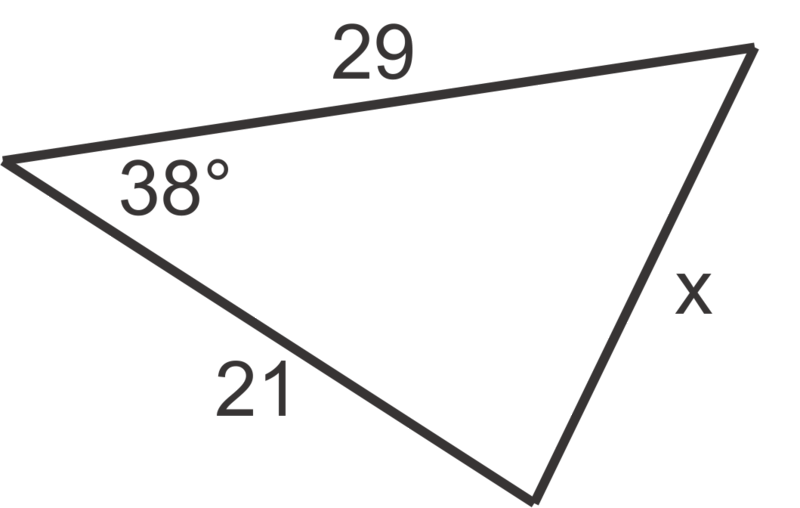
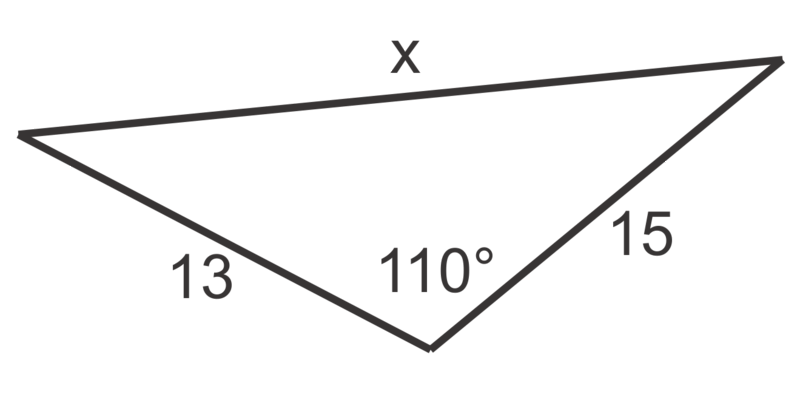
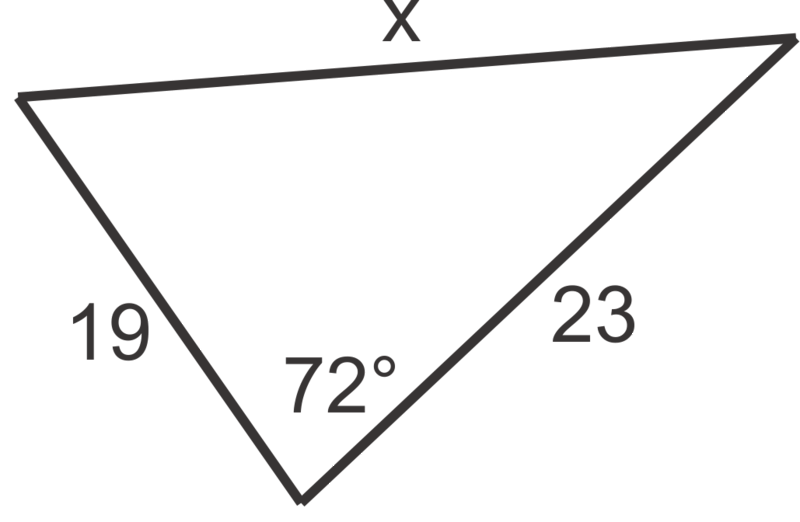
::使用科辛斯定律在问题1至6中找到x的值,至最近的十分点。

For problems 7 through 10, find the unknown side of the triangle. Round your answers to the nearest tenth.
::对于问题 7 到 10, 找到三角形的未知边。将您的答案绕到最近的 10 。

Find $\begin{align*}c\end{align*}$ , given $\begin{align*}m \angle C=105^\circ\end{align*}$ , $\begin{align*}a = 55\end{align*}$ and $\begin{align*}b = 61\end{align*}$ .
::查找 c, 给定 mC=105, a=55 和 b=61。

Find $\begin{align*}b\end{align*}$ , given $\begin{align*}m \angle B=26^\circ\end{align*}$ , $\begin{align*}a = 33\end{align*}$ and $\begin{align*}c = 24\end{align*}$ .
::查找 b, 给定 mB=26 , a= 33 和 c= 24 。

Find $\begin{align*}a\end{align*}$ , given $\begin{align*}m \angle A=77^\circ\end{align*}$ , $\begin{align*}b = 12\end{align*}$ and $\begin{align*}c = 19\end{align*}$ .
::查找 a, 给定 mA=77, b=12 和 c=19 。

Find $\begin{align*}b\end{align*}$ , given $\begin{align*}m \angle B=95^\circ\end{align*}$ , $\begin{align*}a = 28\end{align*}$ and $\begin{align*}c = 13\end{align*}$ .
::查找 b, 给定 mB=95, a=28 和 c=13 。

Explain why when $\begin{align*}m \angle C=90^\circ\end{align*}$ , the Law of Cosines becomes the Pythagorean Theorem.
::解释为什么当 mC=90, 科辛斯定律成为毕达哥里安神话。

Luis is designing a triangular patio in his backyard. One side, 20 ft long, will be up against the side of his house. A second side is bordered by his wooden fence. If the fence and the house meet at a $\begin{align*}120^\circ\end{align*}$ angle and the fence is 15 ft long, how long is the third side of the patio?
::Luis正在其后院设计三角庭院。一边, 20英尺长, 将站在他家的侧面。另一边, 与他的木墙相邻。如果栅栏和房子在120英尺角相交, 栅栏是15英尺长, 院子的第三边还要多久?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

使用SAS的Casine定律(寻找第三面)

Law of Cosines ::科士法

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Law of Cosines
::科士法

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)