课程： 13.17 Heron三角区和用三角测量法解决问题的海隆公式

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节三角区和用三角度量法解决问题的海隆公式

折叠展开
三角区和用三角度量法解决问题的海隆公式
Sarine draws a triangle and measures its sides as 2 inches, 5 inches and 6 inches. What is the area of her triangle?
::沙林绘制一个三角形,用两英寸、五英寸和六英寸测量其侧面。她的三角形的面积是多少?

Heron's Formula
::海隆的方程式

Heron’s Formula, named after Hero of Alexandria 2000 years ago, can be used to find the area of a triangle given the three side lengths. The formula requires the semi-perimeter, $\begin{align*}s\end{align*}$ , or $\begin{align*}\frac{1}{2}(a+b+c)\end{align*}$ , where $\begin{align*}a, b\end{align*}$ and $\begin{align*}c\end{align*}$ are the lengths of the sides of the triangle.
::以亚历山德里亚2000年前的英雄命名的Heron公式可以用来根据三边长度找到三角形的区域。公式要求半边(s)或12(a+b+c),其中a、b和c是三角形两边的长度。

Heron’s Formula:
$\begin{aligned} Area = \sqrt{s (s - a) (s - b) (s - c)} \end{aligned}$
$\begin{align*}\text{Area} =\sqrt{s(s-a)(s-b)(s-c)}\end{align*}$
::Heron的公式:面积(s-a)(s-b)(s-c)

Let's use Heron’s formula to find the area of a triangle with side lengths 13 cm, 16 cm and 23 cm.
::让我们使用Heron的公式来找到边长13厘米、16厘米和23厘米的三角形区域。

First, find the semi-perimeter or $\begin{align*}s\end{align*}$ : $\begin{align*}s=\frac{1}{2}(13+16+23)=26\end{align*}$ . Next, substitute our values into the formula as shown and evaluate:
::首先,找到半外围线或s:s=12(13+16+23)=26。接下来,将我们的值替换为所示的公式并进行评估:

$\begin{aligned} A = \sqrt{26 (26 - 13) (26 - 16) (26 - 23)} = \sqrt{26 (13) (10) (3)} = \sqrt{10140} \approx 101 c m^{2} \end{aligned}$
$\begin{align*}A=\sqrt{26(26-13)(26-16)(26-23)}=\sqrt{26(13)(10)(3)}=\sqrt{10140} \approx 101 \ cm^2\end{align*}$
::A=26(26)-(13)-(26)-16(26-23)=26(13)-(10)(3)=10140)-(101)-(cm2)

Now, let's answer the following questions.
::现在,让我们回答以下的问题。

Alena is planning a garden in her yard. She is using three pieces of wood as a border. If the pieces of wood have lengths 4 ft, 6ft and 3 ft, what is the area of her garden?
::Alena正在计划在其院子里建造花园,她用三块木头作为边界,如果木头的长度是4英尺、6英尺和3英尺,她的花园面积是多少?

The garden will be triangular with side lengths 4 ft, 6 ft and 3 ft. Find the semi-perimeter and then use Heron’s formula to find the area.
::花园的边长为4英尺、6英尺和3英尺。找到半外围计,然后用Heron的公式找到这个区域。

$\begin{aligned} s & = \frac{1}{2} (4 + 6 + 3) = \frac{13}{2} \\ A & = \sqrt{\frac{13}{2} (\frac{13}{2} - 4) (\frac{13}{2} - 6) (\frac{13}{2} - 3)} = \sqrt{\frac{13}{2} (\frac{5}{2}) (\frac{1}{2}) (\frac{7}{2})} = \sqrt{\frac{455}{16}} \approx 28 f t^{2} \end{aligned}$
$\begin{align*}s &=\frac{1}{2}(4+6+3)=\frac{13}{2} \\ A &=\sqrt{\frac{13}{2} \left(\frac{13}{2} -4 \right) \left(\frac{13}{2} -6 \right) \left(\frac{13}{2} -3 \right)}=\sqrt{\frac{13}{2} \left(\frac{5}{2} \right) \left(\frac{1}{2} \right) \left(\frac{7}{2} \right)}=\sqrt{\frac{455}{16}} \approx 28 \ ft^2\end{align*}$
::=12(4+6+3)=132A=132(132-4)(132-6)(132-6)(132-3)=132(52)(12)(72)=4551628英尺

Caroline wants to measure the height of a radio tower. From some distance away from the tower, the angle of elevation from her spot to the top of the tower is $\begin{align*}65^\circ\end{align*}$ . Caroline walks 100 m further away from the tower and measures the angle of elevation to the top of tower to be $\begin{align*}48^\circ\end{align*}$ . How tall is the tower?
::Caroline想测量无线电塔的高度。从离塔的距离,从她的位置到塔顶的高度角度是65英寸。Caroline走在离塔更远100米的地方,测量高到塔顶的高度角度是48英寸。这个塔有多高?

First, make a diagram to illustrate the situation.
::首先,绘制一个图表来说明情况。

We can use angle properties (linear pair and triangle sum) to find the angles shown in green in the diagram.
::我们可以使用角度属性(线性对子和三角形总和)来查找图表中绿色显示的角度。

$\begin{align*}180^\circ-65^\circ=115^\circ\end{align*}$ and $\begin{align*}180^\circ-48^\circ-115^\circ=17^\circ\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Next, we can use the in the obtuse triangle to find the hypotenuse in the right triangle:
::接下来,我们可以在隐形三角形中找到右三角形的下限:

$\begin{aligned} \frac{\sin 17^{\circ}}{100} & = \frac{\sin 48^{\circ}}{x} \\ x & = \frac{100 \sin 48^{\circ}}{\sin 17^{\circ}} \approx 254.18 \end{aligned}$
$\begin{align*}\frac{\sin 17^\circ}{100} &=\frac{\sin 48^\circ}{x} \\ x &=\frac{100 \sin 48^\circ}{\sin 17^\circ} \approx 254.18\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不

Finally we can use the sine ratio in the right triangle to find the height of the tower:
::最后,我们可以使用右三角形的正弦比来找到塔的高度:

$\begin{align*}\sin 65^\circ=\frac{h}{254.18}, h=254.18 \sin 65^\circ \approx 230.37 \ m\end{align*}$
::=254.18sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\30.37米

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the area of the triangle with sides of length 2 inches, 5 inches, and 6 inches.
::早些时候,有人要求你找到三角形的区域,两英寸长,五英寸长,六英寸长。

First, find the semi-perimeter or $\begin{align*}s\end{align*}$ : $\begin{align*}s=\frac{1}{2}(2+5+6)=6.5\end{align*}$ . Next, substitute our values into Heron's formula and evaluate:
::首先,找到半外围线或s:s=12(2+5+6)=6.5。接下来,将我们的值替换成Heron的公式,并评估:

$\begin{aligned} A = \sqrt{6.5 (6.5 - 2) (6.5 - 5) (6.5 - 6)} = \sqrt{6.5 (4.5) (1.5) (0.5)} = \sqrt{21.94} \approx 4.7 i n .^{2} \end{aligned}$
$\begin{align*}A=\sqrt{6.5(6.5-2)(6.5-5)(6.5-6)}=\sqrt{6.5(4.5)(1.5)(0.5)}=\sqrt{21.94} \approx 4.7 \ in.^2\end{align*}$
::A=6.5(6.5-2)(6.5-5)(6.5-6)=6.5(4.5)(1.5)(0.5)=21.944.7英寸。

Use the most appropriate rule or formula (Law of Sines, , area formula with sine or Heron’s formula) to answer the following questions.
::使用最适当的规则或公式(Sines法、Sines公式、reaty公式或Heron公式)回答下列问题。

Example 2
::例2

Find the area of a triangle with side lengths 50 m, 45 m and 25 m.
::查找侧长50米、45米和25米的三角形区域。

Heron’s Formula: $\begin{align*}s=\frac{1}{2}(50+45+25)=60, A=\sqrt{60(60-50)(60-45)(60-25)} \approx 561 \ m^2\end{align*}$ .
::Heron的公式:S=12(50+45+25)=60,A=60(60-50)(60-45)(60-25)=561平方米。

Example 3
::例3

Matthew is planning to fertilize his grass. Each bag of fertilizer claims to cover 500 sq ft of grass. His property of land is approximately in the shape of a triangle. He measures two sides of his yard to be 75 ft and 100 ft and the angle between them is $\begin{align*}72^\circ\end{align*}$ . How many bags of fertilizer must he buy?
::马修计划施肥他的草。每袋肥料都声称覆盖500平方英尺的草。他的地产大致是三角形。他将院子的两边测量成75平方和100平方英尺,两边的角是72平方英尺。他必须买多少袋肥料?

Area formula with sine: $\begin{align*}\frac{1}{2}(75)(100) \sin 72^\circ \approx 3566 \ ft^2\end{align*}$ , Number of bags $\begin{align*}\frac{3566}{500} \approx 7.132 \approx 8\end{align*}$ bags. We round up because 7 bags is not quite enough.
::区域公式正弦值: 12 (75) (100sin723566 ft2, 袋数: 35665007. 1328 袋数。我们聚集在一起是因为有7个袋不够用。

Example 4
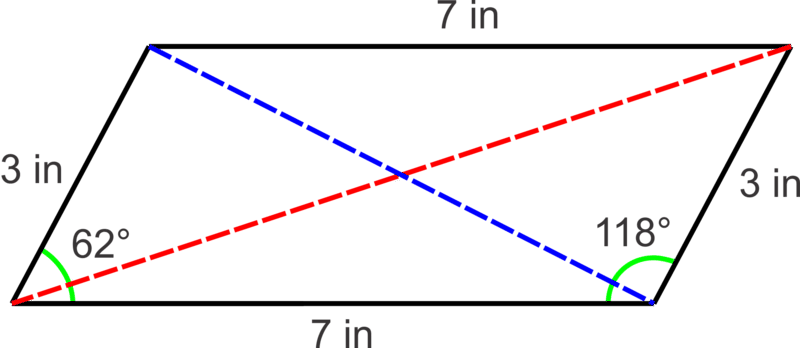
::例4

A pair of adjacent sides in a parallelogram are 3 in and 7 in and the angle between them is $\begin{align*}62^\circ\end{align*}$ , find the length of the diagonals.
::一对相邻的侧面的平行图是3和7,它们之间的角是62,找到对角线的长度。

Law of Cosines to find the blue diagonal:
::寻找蓝色对角线的科辛斯定律:

$\begin{aligned} c^{2} & = 3^{2} + 7^{2} - 2 (3) (7) \cos 62^{\circ} \\ c & = \sqrt{38.28} \approx 6.19 \end{aligned}$
$\begin{align*}c^2 &=3^2+7^2-2(3)(7) \cos 62^\circ \\ c &=\sqrt{38.28} \approx 6.19\end{align*}$ So, 6.19 in
::c2=32+72-2(3)(7)(7)cos62c=38.286.19 So, 6.19 in

To find the green diagonal we can use the Law of Cosines with the adjacent angle: $\begin{align*}180^\circ-62^\circ-118^\circ\end{align*}$ :
::为了找到绿色对角形, 我们可以使用近角的科辛斯定律:18062118:

$\begin{aligned} c^{2} & = 7^{2} + 3^{2} - 2 (7) (3) \cos 118^{\circ} \\ c & = \sqrt{77.72} \approx 8.82 \end{aligned}$
$\begin{align*}c^2 &=7^2+3^2-2(7)(3) \cos 118^\circ \\ c &=\sqrt{77.72} \approx 8.82\end{align*}$ So, 8.82 in
::c2=72+32-2(7)(3)cos118c=77.72.728.82 So 8.82 in

Review
::回顾

Use the Law of Sines, Law of Cosine, area of triangle with sine or Heron’s Formula to solve the real world application problems.
::使用Sines法、Casine法、带有正弦或Heron公式的三角区域来解决真正的世界应用问题。

Two observers, Rachel and Luis, are standing on the shore, 0.5 miles apart. They each measure the angle between the shoreline and a sailboat out on the water at the same time. If Rachel’s angle is $\begin{align*}63^\circ\end{align*}$ and Luis’ angle is $\begin{align*}56^\circ\end{align*}$ , find the distance between Luis and the sailboat to the nearest hundredth of a mile.
::有两个观察家 — — 瑞秋和路易斯(Rachel和Luis) — — 站在海岸上,相距0.5英里。他们各自同时测量海岸线和一艘帆船在水面上之间的角。如果Rachel的角是63°Z,而Luis的角是56°Z,请找到Luis和帆船之间的距离,距离是距离最近的100英里。如果Rachel的角是63°Z,而Luis的角是56°Z,请找到Luis和帆船之间的距离。

Two pedestrians walk from opposite ends of a city block to a point on the other side of the street. The angle formed by their paths is $\begin{align*}125^\circ\end{align*}$ . One pedestrian walks 300 ft and the other walks 320 ft. How long is the city block to the nearest foot?
::两个行人从一个城市街区的对面步行到另一条街道的一个点,他们的行道所形成的角度是125英尺。一个行人行走300英尺,另一个行人行走320英尺。城市街区离最近的脚还有多久?

Two sides and the included angle of a parallelogram have measures 3.2 cm, 4.8 cm and $\begin{align*}54.3^\circ\end{align*}$ respectively. Find the lengths of the diagonals to the nearest tenth of a centimeter.
::两面和包含的平行图角分别测量3.2厘米、4.8厘米和54.3英寸。

A bridge is supported by triangular braces. If the sides of each brace have lengths 63 ft, 46 ft and 40 ft, find the measure of the largest angle to the nearest degree.
::桥梁由三角形支架支撑。如果每个支架的两侧长度为63英尺、46英尺和40英尺,则可以找到距离最近的最大角度。

Find the triangular area, to the nearest square meter, enclosed by three pieces of fencing 123 m, 150 m and 155 m long.
::寻找最接近平方平方米的三角区域,以三块123米、150米和155米长的栅栏围住。

Find the area, to the nearest square inch, of a parallelogram with sides of length 12 in and 15 in and included angle of $\begin{align*}78^\circ\end{align*}$ .
::找到最接近平方英寸的区域,以78角为角,其侧角为12英寸和15英寸,并包括78角。

A person at point $\begin{align*}A\end{align*}$ looks due east and spots a UFO with an angle of elevation of $\begin{align*}40^\circ\end{align*}$ . At the same time, another person, 1 mi due west of A looks due east and sights the same UFO with an angle of elevation of $\begin{align*}25^\circ\end{align*}$ . Find the distance between $\begin{align*}A\end{align*}$ and the UFO. How far is the UFO above the ground? Give answers to the nearest hundredth of a mile.
::A点上的人向东看,发现UFO的高度为40°Q。同时,A点上的另一个人,即A点以西1米处向东看,看到同一UFO的高度为25°C。找到A点与UFO之间的距离。UFO在地面上方有多远?回答最近的100英里。

Find the area of a triangular playground, to the nearest square meter, with sides of length 10 m, 15 m and 16 m.
::寻找三角运动场的面积,至最近的平方平方米,两边的长度为10米、15米和16米。

A yard is bounded on two sides with fences of length 80 ft and 60 ft. If these fences meet at a $\begin{align*}75^\circ\end{align*}$ angle, how many feet of fencing are required to completely enclosed a triangular region?
::院子两侧有80英尺长和60英尺长的栅栏。如果这些栅栏在75英寸角相交,则需要多少英尺的栅栏才能完全封闭三角区域?

When a boy stands on the bank of a river and looks across to the other bank, the angle of depression is $\begin{align*}12^\circ\end{align*}$ . If he climbs to the top of a 10 ft tree and looks across to other bank, the angle of depression is $\begin{align*}15^\circ\end{align*}$ . What is the distance from the first position of the boy to the other bank of the river? How wide is the river? Give your answers to the nearest foot.
::当一个男孩站在河岸对面看着另一条河岸时,萧条的角是12英寸。如果他爬到10英尺树的顶部,然后望到另一条河岸,萧条的角是15英尺。从男孩的第一位置到河另一边的距离是多少?河的宽度是多少?给最近的脚提供答案。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

三角区和用三角度量法解决问题的海隆公式

Heron's Formula ::海隆的方程式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Heron's Formula
::海隆的方程式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)