14.2 转化松和余弦函数

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 转换正弦和余弦函数

  Collapse Expand

  转换正弦和余弦函数

  播放段落

  Your best friend asks you to describe how the graph of $\begin{align*}y= \sin (x-\pi)-2\end{align*}$ is different from the graph of $\begin{align*}y= \sin x\end{align*}$ . What do you tell your friend?
  ::您最好的朋友要您描述 y=sin( x)- 2 的图形与 y=sinx 的图形有何不同。 您要告诉您的朋友什么 ?

  播放段落

  Translating Sine and Cosine Functions
  ::转换正弦和余弦函数

  播放段落

  Just like other functions, curves can be moved to the left, right, up and down. The general equation for a sine and cosine curve is $\begin{align*}y=a \sin (x-h)+k\end{align*}$ and $\begin{align*}y=a \cos(x-h)+k\end{align*}$ , respectively. Also, just like in other functions, $\begin{align*}h\end{align*}$ is the horizontal shift, also called a phase shift , and $\begin{align*}k\end{align*}$ is the vertical shift . Notice, that because it is $\begin{align*}x - h\end{align*}$ in the equation, $\begin{align*}h\end{align*}$ will always shift in the opposite direction of what is in the equation.
  ::与其他函数一样, 曲线可以向左、 右、 上、 下移动。 正弦和正弦曲线的一般方程分别是 y=asin( x-h)+k 和 y=asos( x-h)+k 。 与其他函数一样, h 是水平转换, 也称为 阶段转换, k 是垂直转换 。 注意, 由于正弦和正弦曲线是 x-h , h 总是会向正方程的相反方向移动 。

  播放段落

  Let's graph $\begin{align*}y=\cos \left(x - \frac{\pi}{4}\right)\end{align*}$ .
  ::让我们用图y=cos(x% 4) 来图解 y=cos(x% 4) 。

  播放段落

  This function will be shifted $\begin{align*}\frac{\pi}{4}\end{align*}$ units to the right. The easiest way to sketch the curve, is to start with the parent graph and then move it to the right the correct number of units.
  ::此函数将被移到右侧 4 个单位。 最容易绘制曲线的方法是从父图形开始, 然后将其移到右侧, 正确的单位数 。

  

  播放段落

  Now, let's graph $\begin{align*}y=\sin (x+2)+3\end{align*}$ .
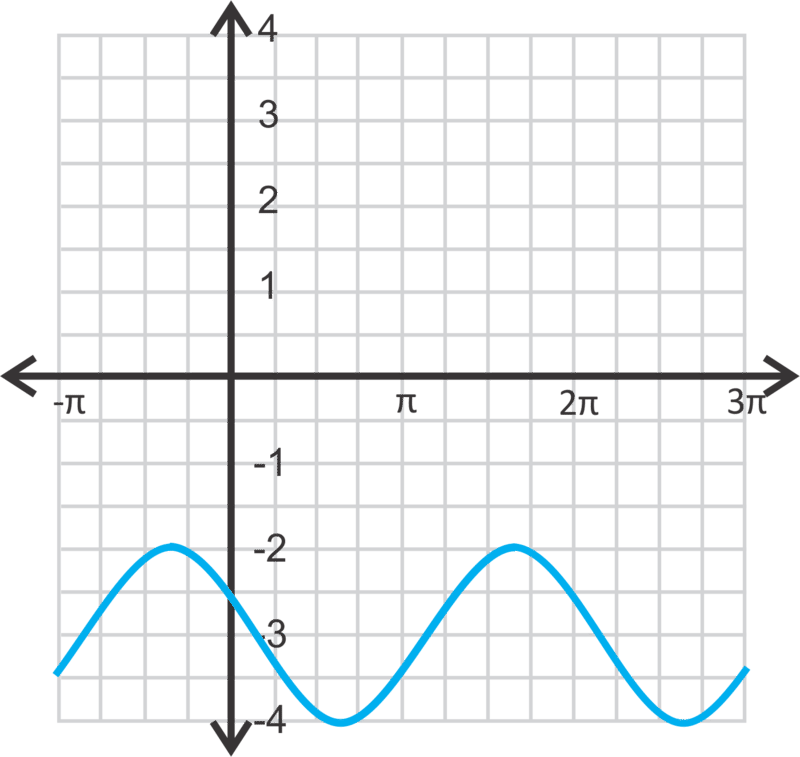
  ::现在,让我们用图y=sin( x+2)+3来表示。

  播放段落

  Because -2 is not written in terms of $\begin{align*}\pi\end{align*}$ (like the $\begin{align*}x\end{align*}$ -axis), we need to estimate where it would be on the axis. $\begin{align*}- \frac{3 \pi}{4}=2.35 \ldots\end{align*}$ So, -2 will be shifted not quite to the $\begin{align*}- \frac{3 \pi}{4}\end{align*}$ tic mark. Then, the entire function will be shifted up 3 units. The red graph is the final answer.
  ::-2不是以 {( 和 x 轴一样) 写成的, 我们需要估计轴上的位置 。 -3}4=2.35... 所以, -2 将不完全移到 3§4 的标记上。 然后, 整个函数会向上移动 3 个单位。 红色图是最后答案 。

  

  播放段落

  Finally, let's find the equation of the sine curve below.
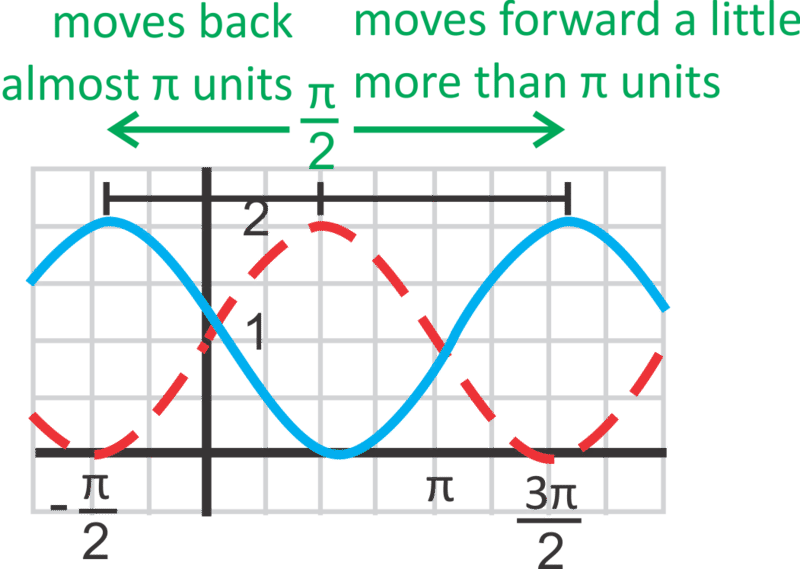
  ::最后,让我们在下面找到正弦曲线的方程。

  

  播放段落

  First, we know the is 1 because the average between 2 and 0 (the maximum and minimum) is 1. Next, we can find the vertical shift. Recall that the maximum is usually 1, in this equation it is 2. That means that the function is shifted up 1 unit $\begin{align*}(2-1)\end{align*}$ . The horizontal shift is the hardest to find. Because sine curves are periodic, the horizontal shift can either be positive or negative.
  ::首先,我们知道是1,因为2到0之间的平均值(最大值和最小值)是1。接下来,我们可以找到垂直变化。在此方程中,回顾最大值通常为1,在此方程中是2。这意味着函数向上移动1个单位(2-1),横向变化是最难找到的。由于正弦曲线是周期性的,横向变化可以是正的,也可以是负的。

  播放段落

  Because $\begin{align*}\pi\end{align*}$ is $\begin{align*}3.14 \ldots\end{align*}$ , we can say that “moves back almost $\begin{align*}\pi\end{align*}$ units” is -3 units. So, the equation is $\begin{align*}y=\sin (x+3)+1\end{align*}$ . If we did the positive horizontal shift, we could say that the equation would be $\begin{align*}y=\sin (x-3.28)+1\end{align*}$ .
  ::因为 □ 是 3. 14..., 我们可以说“ 移动后几乎 □ 单位” 是 - 3 单位。 所以, 等式是 y=sin( x+3) +1. 如果我们做了正水平转换, 我们可以说 y=sin( x-3. 28) +1 等式是 y=sin( x-3. 28) +1 。

  

  播放段落

  To determine the value of the horizontal shift, you might have to estimate. For example, we estimated that the negative shift was -3 because the maximum value of the parent graph is at $\begin{align*}x=\frac{\pi}{2}\end{align*}$ and the maximum to the left of it didn’t quite make it to $\begin{align*}x=- \frac{\pi}{2}\end{align*}$ (the distance between $\begin{align*}\frac{\pi}{2}\end{align*}$ and $\begin{align*}-\frac{\pi}{2}\end{align*}$ is $\begin{align*}\pi\end{align*}$ ). Then, to determine the positive shift equation, recall that a period is $\begin{align*}2 \pi\end{align*}$ , which is $\begin{align*}6.28 \ldots\end{align*}$ So, the positive shift would be $\begin{align*}2 \pi - 3\end{align*}$ or $\begin{align*}6.28 - 3 = 3.28.\end{align*}$ .
  ::为了确定水平转换的值, 您可能需要估计。 例如, 我们估计负变化是 - 3, 因为母图的最大值是 x2, 左侧的最大值没有完全达到 x2 。 然后, 要确定正变化方程, 请记住一个时间段是 22, 也就是 6. 28... 所以正变化是 23 或 6. 28 - 3= 3. 28 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to tell your friend how the graph of  $\begin{align*}y= \sin (x-\pi)-2\end{align*}$  is different from the graph of  $\begin{align*}y = \sin x\end{align*}$ . 
  ::早些时候,有人要求你告诉朋友y=sin(x)-2的图与y=sinx的图有何不同。

  播放段落

  If you compare $\begin{align*}y= \sin (x-\pi)-2\end{align*}$ to the general equation $\begin{align*}y=a \sin(x-h)+k\end{align*}$ , you see that $\begin{align*}h=\pi\end{align*}$ and $\begin{align*}k=-2\end{align*}$ .
  ::如果您比较 y=sin( x)-2 和 y=asin( x-h)+k 等式, 您可以看到 h 和 k 2 。

  播放段落

  $\begin{align*}h\end{align*}$ is the horizontal shift, so the function is $\begin{align*}\pi\end{align*}$ units to the right of $\begin{align*}y= \sin x\end{align*}$ .
  ::h 是水平移动, 所以函数是 y=sinx 右边的 __ 单位 。

  播放段落

  $\begin{align*}k\end{align*}$ is the vertical shift, so the function is 2 units down from $\begin{align*}y= \sin x\end{align*}$ .
  ::k 是垂直移动, 所以函数从 y=sinx 向下是 2 个单位 。

  播放段落

  Therefore, the graph of $\begin{align*}y= \sin (x-\pi)-2\end{align*}$ is shifted $\begin{align*}\pi\end{align*}$ units to the right and two units down from the graph of $\begin{align*}y= \sin x\end{align*}$ .
  ::因此, y=sin(x)-2 的图被移到右侧, 从 y=sinx 的图中向下移了两个单位 。

  播放段落

  In Examples 2 & 3, g raph the function from $\begin{align*}[\pi, 3 \pi]\end{align*}$ .
  ::在例2和例3中,请用 [_,3__] 绘制函数图。

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{align*}y=-1+\sin x\end{align*}$
  ::y1+sinx y1+sinx y1+sinx

  播放段落

  Shift the parent graph down one unit.
  ::将母图向下移动一个单位。

  

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{align*}y=\cos\left(x+\frac{\pi}{3}\right) - 2\end{align*}$
  ::y=cos(x%3)- 2

  播放段落

  Shift the parent graph to the left $\begin{align*}\frac{\pi}{3}\end{align*}$ units and down 2 units.
  ::将父图移到左+++3 单位, 向下移到 2 个单位 。

  

  播放段落

  Example 4
  ::例4

  播放段落

  Find the equation of the cosine curve below.
  ::在下面查找余弦曲线的方程。

  

  播放段落

  The parent graph is in green. It moves up 3 units and to the right $\begin{align*}\frac{3 \pi}{4}\end{align*}$ units. Therefore, the equation is $\begin{align*}y=\cos \left(x-\frac{3 \pi}{4}\right)+3\end{align*}$ .
  ::父图以绿色表示。 它向上移动 3 个单位, 向右移动 3 4 个单位。 因此, 公式是 y=cos( x-3 4)+ 3 。

  

  播放段落

  If you moved the cosine curve backward, then the equation would be $\begin{align*}y=\cos \left(x+\frac{5 \pi}{4}\right)+3\end{align*}$ .
  ::如果将余弦曲线向后移动,则公式为y=cos(x+5+4)+3。

  播放段落

  Review
  ::回顾

  播放段落

  For questions 1-4, match the equation with its graph.
  ::对于问题14, 问题14, 将方程式与其图表匹配 。

  

  播放段落
  1. $\begin{align*}y=\sin \left(x-\frac{\pi}{2}\right)\end{align*}$
     ::y=sin(x2)
  播放段落
  2. $\begin{align*}y=\cos \left(x-\frac{\pi}{4}\right)+3\end{align*}$
     ::y=cos( x4)+3
  播放段落
  3. $\begin{align*}y=\cos \left(x+\frac{\pi}{4}\right)-2\end{align*}$
     ::y=cos(x%4)-2
  播放段落
  4. $\begin{align*}y=\sin \left(x-\frac{\pi}{4}\right)+2\end{align*}$
     ::y=sin( x4)+2

  播放段落

  Which graph above also represents these equations?
  ::以上哪个图表也代表这些方程式?

  播放段落
  5. $\begin{align*}y=\cos(x-\pi)\end{align*}$
     ::y=cos(x)
  播放段落
  6. $\begin{align*}y=\sin \left(x+\frac{3 \pi}{4}\right)-2\end{align*}$
     ::y=sin( x+3+4)-2
  播放段落
  7. Write another sine equation for graph A.
     ::为图A写一个正弦方程。
  播放段落
  8. Writing How many sine (or cosine) equations can be generated for one curve? Why?
     ::写入一个曲线可以生成多少正弦( 或余弦) 方程式 ? 为什么 ?
  播放段落
  9. Fill in the blanks below.
     播放段落
     1. $\begin{align*}\sin x=\cos(x-\underline{\;\;\;\;\;})\end{align*}$
        ::sinx=cos(x)
     播放段落
     2. $\begin{align*}\cos x=\sin(x-\underline{\;\;\;\;\;})\end{align*}$
        ::COsx=sin(x)
     
     ::填充下面的空白。 sinx=cos(x) cosx=sin(x)

  播放段落

  For questions 10-15, graph the following equations from $\begin{align*}[-2\pi, 2\pi]\end{align*}$ .
  ::关于问题10-15, 如下方程式,取自[-2 2]。

  播放段落
  10. $\begin{align*}y=\sin \left(x+\frac{\pi}{4}\right)\end{align*}$
      ::y=sin(x4)
  播放段落
  11. $\begin{align*}y=1+\cos x\end{align*}$
      ::y=1+cosx y=1+cosx
  播放段落
  12. $\begin{align*}y=\cos(x+\pi)-2\end{align*}$
      ::y=cos(x)-2
  播放段落
  13. $\begin{align*}y=\sin(x+3)-4\end{align*}$
      ::y=sin( x+3)- 4
  播放段落
  14. $\begin{align*}y=\sin \left(x-\frac{\pi}{6}\right)\end{align*}$
      ::y=sin(x6)
  播放段落
  15. $\begin{align*}y=\cos(x-1)-3\end{align*}$
      ::y=cos( x- 1) - 3
  播放段落
  16. Critical Thinking Is there a difference between $\begin{align*}y=\sin x +1\end{align*}$ and $\begin{align*}y=\sin(x+1)\end{align*}$ ? Explain your answer.
      ::关键思考 y= sinx+1 和 y=sin( x+1) 之间有区别吗? 请解释您的答案 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。