Course: 14.3 将所有这一切放在一起 | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 将所有这一切放在一起

Collapse Expand
将所有这一切放在一起
Your mission, should you choose to accept it, as Agent Trigonometry is to the find the domain and the range of the function $\begin{aligned} y = \frac{1}{2} \sin (x + 2) - 3 \end{aligned}$ .
::您的任务, 如果您选择接受它, 因为Trigono量度代理是找到域和函数 y= 12sin( x+2) - 3 的范围。

Graphing Functions
::图图函数

Here you'll change the , the horizontal shifts, vertical shifts , and reflections.
::在这里,你将改变, 横向的转变,垂直的转变, 和反射。

Let's graph $\begin{aligned} y = 4 \sin (x - \frac{π}{4}) \end{aligned}$ and find the domain and range.
::让我们绘制 y= 4sin(x4) 并找到域和范围。

First, stretch the curve so that the amplitude is 4, making the maximums and minimums 4 and -4. Then, shift the curve $\begin{aligned} \frac{π}{4} \end{aligned}$ units to the right.
::首先,拉伸曲线,使振幅为 4 , 使最大和最小值为 4 和 - 4 。然后, 将曲线 + 4 单位向右移动。

As for the domain, it is all real numbers because the sine curve is periodic and infinite. The range will be from the maximum to the minimum; $\begin{aligned} y \in [- 4, 4] \end{aligned}$ .
::至于域,它都是真实的数字, 因为正弦曲线是周期性的, 无限的。范围从最大到最小; y y [- 4, 4] 。

Now, let's graph $\begin{aligned} y = - 2 \cos (x - 1) + 1 \end{aligned}$ and find the domain and range.
::现在,让我们来绘制 y2cos (x- 1) +1, 并找到域名和范围。

The -2 indicates the cosine curve is flipped and stretched so that the amplitude is 2. Then, move the curve up one unit and to the right one unit.
::-2表示余弦曲线被翻转和拉伸,使振幅为2,然后将曲线向上移动一个单位,向右移动一个单位。

The domain is all real numbers and the range is $\begin{aligned} y \in [- 1, 3] \end{aligned}$ .
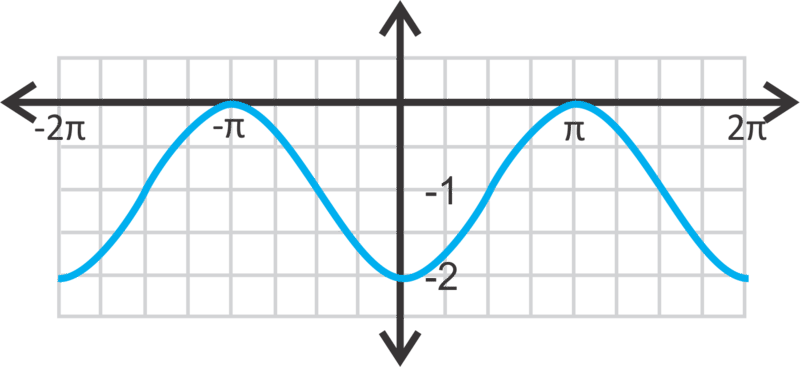
::域名是所有真实数字,范围是y[-1,3]。

Finally, let's find the equation of the sine curve below.
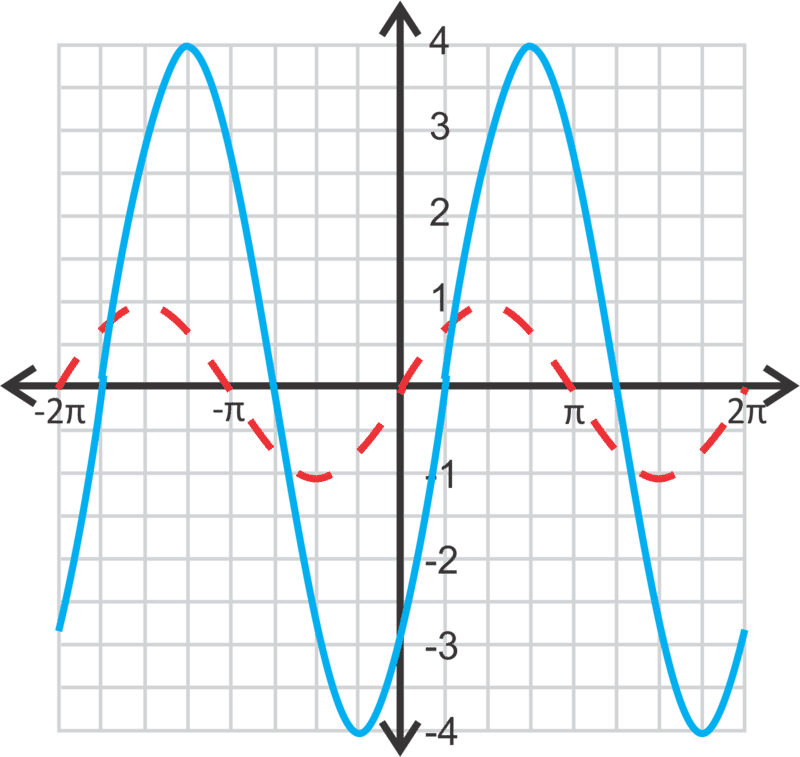
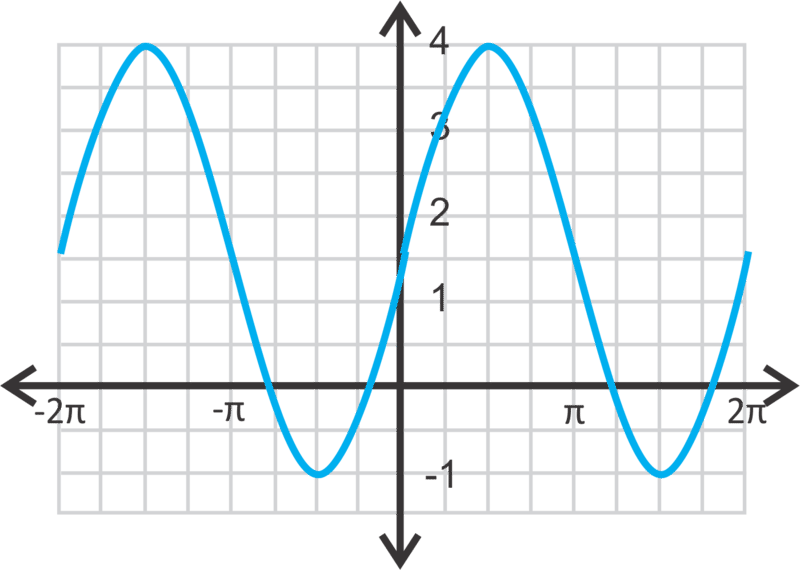
::最后,让我们在下面找到正弦曲线的方程。

First, let’s find the amplitude. The range is from 1 to -5, which is a total distance of 6. Divided by 2, we find that the amplitude is 3. Halfway between 1 and -5 is $\begin{aligned} \frac{1 + (- 5)}{5} = - 2 \end{aligned}$ , so that is our vertical shift. Lastly, we need to find the horizontal shift. The easiest way to do this is to superimpose the curve $\begin{aligned} y = 3 \sin (x) - 2 \end{aligned}$ over this curve and determine the movement from one maximum to the closest maximum of this curve.
::首先,让我们找到振幅。范围从1到5, 总距离是6, 除以2, 我们发现振幅是3, 1到5之间的半径是1+( - 5-5)52, 这就是我们垂直的转变。最后, 我们需要找到横向的转变。最简单的办法是将曲线 y=3sin( x)-2 叠加到这个曲线上, 并确定从这个曲线的最大一个向最接近的最大移动。

Subtracting $\begin{aligned} \frac{π}{2} \end{aligned}$ and $\begin{aligned} \frac{π}{6} \end{aligned}$ , we have:
::以2和6为减号,我们已:

$\begin{aligned} \frac{π}{2} - \frac{π}{6} = \frac{3 π}{6} - \frac{π}{6} = \frac{2 π}{6} = \frac{π}{3} \end{aligned}$

Making the equation $\begin{aligned} y = 3 \sin (x + \frac{π}{3}) - 2 \end{aligned}$ .
::使公式y=3sin(x3)-2。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the domain and range of the function $\begin{aligned} y = \frac{1}{2} \sin (x + 2) - 3 \end{aligned}$ .
::早些时候, 您被要求查找 y= 12sin {( x+2) - 3 函数的域名和范围。

The $\begin{aligned} \frac{1}{2} \end{aligned}$ indicates the sine curve is smooshed so that the amplitude is $\begin{aligned} \frac{1}{2} \end{aligned}$ . Then, move the curve down two units and to the left three units.
::12 表示正弦曲线被打乱, 使振幅为12。然后, 将曲线向下移动两个单位, 向左移动三个单位。

The domain is all real numbers and the range is $\begin{aligned} y \in [- \frac{5}{2}, - \frac{3}{2}] \end{aligned}$ .
::域名是所有实际数字,范围是y[-52,-32]。

For Examples 2 & 3, graph the functions. State the domain and range. Show two full periods.
::对于例2和例3,请绘制函数图。说明域和范围。显示两个完整的周期。

Example 2
::例2

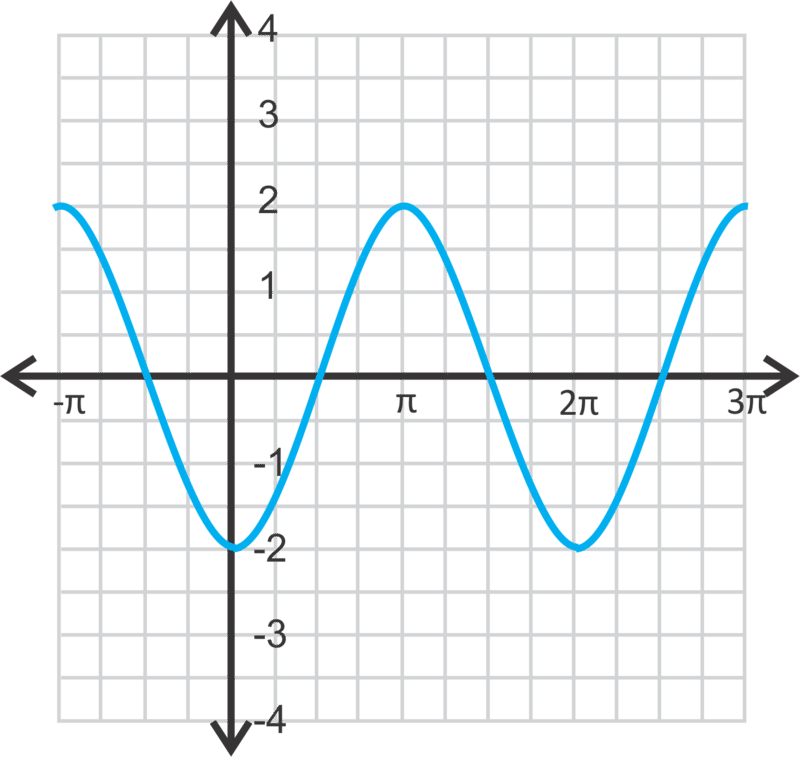
$\begin{aligned} y = - 2 \sin (x - \frac{π}{2}) \end{aligned}$
::y2sin(x%2)

The domain is all real numbers and the range is $\begin{aligned} y \in [- 2, 2] \end{aligned}$ .
::域名是所有真实数字,范围是y[-2,2]。

Example 3
::例3

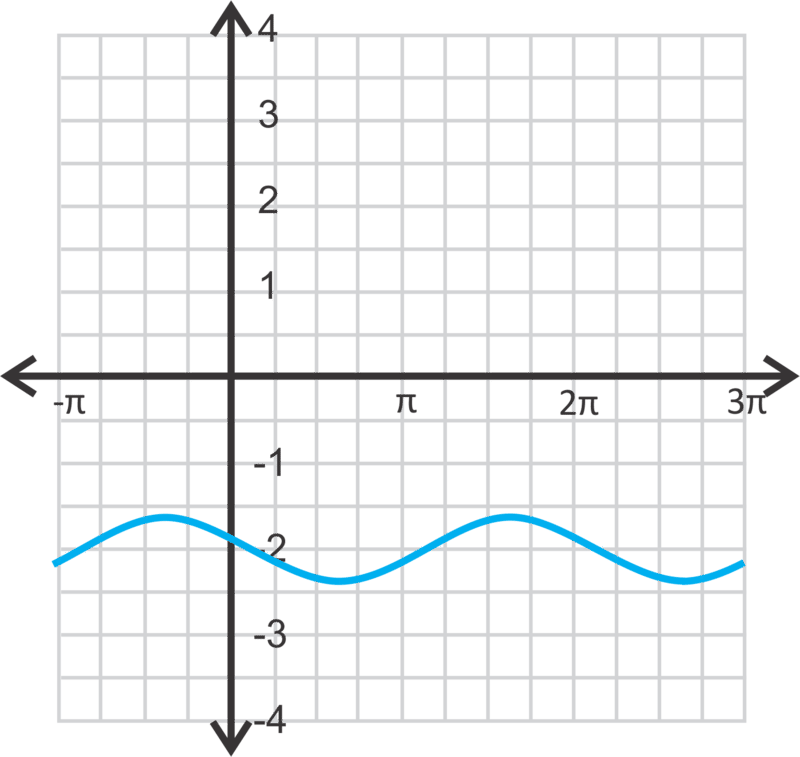
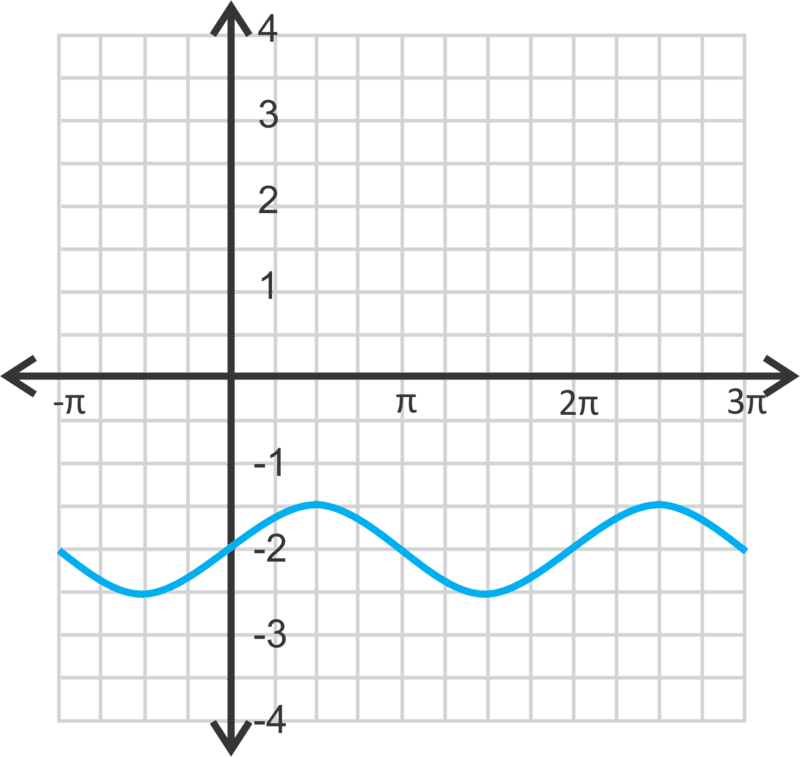
$\begin{aligned} y = \frac{1}{3} \cos (x + 1) - 2 \end{aligned}$
::y=13cos( x+1)-2

The domain is all real numbers and the range is $\begin{aligned} y \in [- 2 \frac{1}{3}, - 1 \frac{2}{3}] \end{aligned}$ .
::域名是所有实际数字,范围是y[-213,-123]。

Example 4
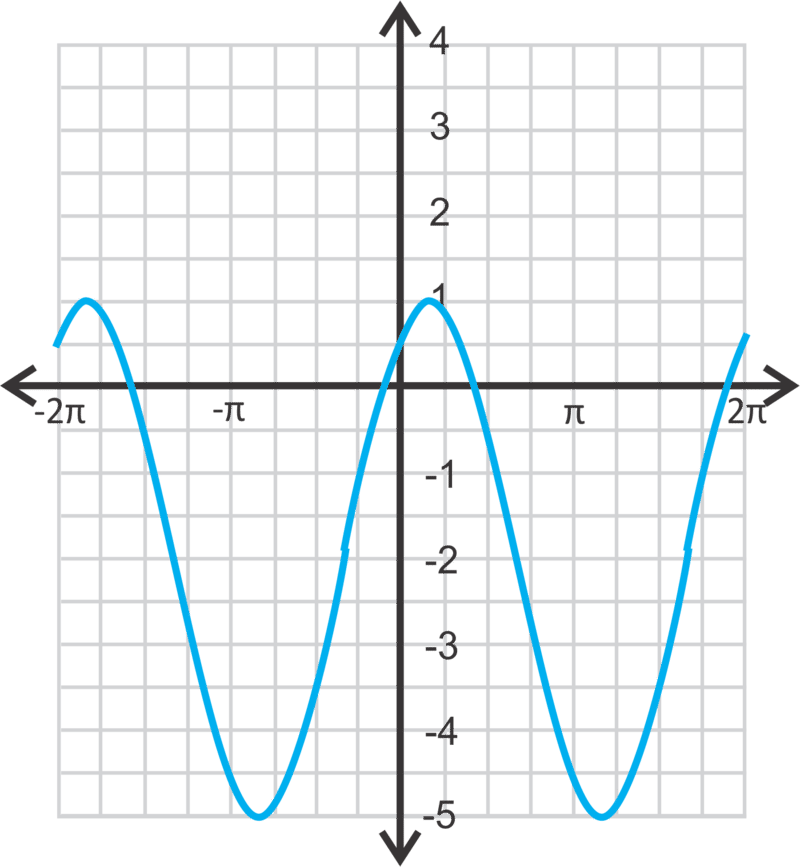
::例4

Write one sine equation and one cosine equation for the curve below.
::为下面的曲线写一个正弦方程和一个正弦方程。

The amplitude and vertical shift is the same, whether the equation is a sine or cosine curve. The vertical shift is -2 because that is the number that is halfway between the maximum and minimum. The difference between the maximum and minimum is 1, so the amplitude is half of that, or $\begin{aligned} \frac{1}{2} \end{aligned}$ . As a sine curve, the function is $\begin{aligned} y = - 2 + \frac{1}{2} \sin x \end{aligned}$ . As a cosine curve, there will be a shift of $\begin{aligned} \frac{π}{2}, y = \frac{1}{2} \cos (x - \frac{π}{2}) - 2 \end{aligned}$ .
::振幅和垂直变化是相同的, 不论方程式是正弦曲线还是正弦曲线。垂直变化是 - 2, 因为数字是最大和最小值之间的一半。最大和最小值之间的差值是 1, 因此振幅是该值的一半, 或12。作为正弦曲线, 函数是 y2+12sinx。作为正弦曲线, 将会有 2, y=12cos( x2)-2 的移动。

Review
::回顾

Determine if the following statements are true or false.
::确定以下声明是真实的还是虚假的。

To change a cosine curve into a sine curve, shift the curve $\begin{aligned} \frac{π}{2} \end{aligned}$ units.
::将余弦曲线改变为正弦曲线,将曲线 2 单位移动。

For any given sine or cosine graph, there are infinitely many possible equations that can be written to represent the curve.
::对于任何给定的正弦或正弦图,可以写出无数可能的方程式来表示曲线。

The amplitude is the same as the maximum value of the sine or cosine curve.
::振幅与正弦或余弦曲线的最大值相同。

The horizontal shift is always in terms of $\begin{aligned} π \end{aligned}$ .
::横向变化总是以为单位。

The domain of any sine or cosine function is always all real numbers.
::任何正弦或余弦函数的域始终是所有实际数字。

Graph the following sine or cosine functions such that $\begin{aligned} x \in [- 2 π, 2 π] \end{aligned}$ . State the domain and range.
::下图的正弦函数或余弦函数为 x[-222]。请标明域和范围。

$\begin{aligned} y = \sin (x + \frac{π}{4}) + 1 \end{aligned}$
::y=sin(x4)+1

$\begin{aligned} y = 2 - 3 \cos x \end{aligned}$
::y=2 - 3cosx

$\begin{aligned} y = \frac{3}{4} \sin (x - \frac{2 π}{3}) \end{aligned}$
::y=34sin(x-23)

$\begin{aligned} y = - 5 \sin (x - 3) - 2 \end{aligned}$
::y5sin(x-3)-2

$\begin{aligned} y = 2 \cos (x + \frac{5 π}{6}) - 1.5 \end{aligned}$
::y=2cos(x+56)-1.5

$\begin{aligned} y = - 2.8 \cos (x - 8) + 4 \end{aligned}$
::y2.8cos(x-8)+4

Use the graph below to answer questions 12-15.
::用下图回答问题12-15。

Write a sine equation for the function where the amplitude is positive.
::为振幅为正数的函数写入正数等式。

Write a cosine equation for the function where the amplitude is positive.
::为振幅为正数的函数写入余弦方程。

How often does a sine or cosine curve repeat itself? How can you use this to help you write different equations for the same graph?
::正弦或余弦曲线的重复频率是多少? 您如何使用它来帮助您为同一图表写出不同的方程式 ?

Write a second sine and cosine equation with different horizontal shifts.
::以不同的水平移动写入二次正弦和连弦方程。

Use the graph below to answer questions 16-20.
::用下图回答问题16-20。

Write a sine equation for the function where the amplitude is positive.
::为振幅为正数的函数写入正数等式。

Write a cosine equation for the function where the amplitude is positive.
::为振幅为正数的函数写入余弦方程。

Write a sine equation for the function where the amplitude is negative .
::在振幅为负值的函数中写入正弦方程。

Write a cosine equation for the function where the amplitude is negative .
::为振幅为负的函数写入余弦方程。

Describe the similarities and differences between the four equations from questions 16-19.
::说明问题16-19的四个方程之间的相似和不同之处。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。