5.11 矢量分析应用

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 矢量分析应用

  Collapse Expand

  矢量分析应用

  播放段落

  How much work is done by a 10kg ball rolling down a 25 ^o slope for 10 yards?
  ::一个10公斤的球在25度的斜坡上滚下10码 做了多少工作?

  播放段落

  How can the force which propels a proton through a magnetic field be calculated?
  ::如何计算推动质子穿过磁场的力量?

  播放段落

  How could you calculate the torque exerted by children on a see-saw?
  ::你怎能计算儿童在锯锯子上施加的扭力呢?

  播放段落

  This lesson is all about real-world uses of vector analysis.
  ::这都是关于现实世界使用矢量分析的教训。

  播放段落

  Vector Analysis Applications
  ::矢量分析应用

  播放段落

  Vectors can be used by air-traffic controllers when tracking planes, by meteorologists when describing wind conditions, and by computer programmers when they are designing virtual worlds. In this section, we will present three applications of vectors which are commonly used in the study of physics: work, torque, and magnetic force.
  ::空中交通控制器在跟踪飞机时、气象学家在描述风情时、计算机程序员在设计虚拟世界时,都可以使用矢量。 在本节中,我们将介绍物理学研究中常用的三种矢量应用:工作、压力和磁力。

  播放段落

  Work
  ::工作 工作 工作 工作

  播放段落

  In physics, the term work is used to describe energy that is added to or removed from an object or system when a force is applied to it. From experiment, it has been determined that work is maximized when the applied force is parallel to the motion of the object and that no work is done when the force is applied perpendicular to the motion. Therefore, the work done by a force can be described by the dot product of the force vector and the displacement vector. For example, several forces act on the skier in the diagram below.
  ::在物理学中,工作一词用来描述在对物体或系统施用一种力量时,该物体或系统的能量被添加或从该物体或系统中去除的能量;通过实验,确定在应用力量与物体运动平行时,工作是最大化的;在施用与该运动相对应的力时,没有做任何工作;因此,一种力量所完成的工作可以用力量矢量和移位矢量的点产物来描述;例如,在下图中,一些力量对滑雪者采取行动。

  

  播放段落

  Sven’s weight pulls downward toward the center of the earth, the snow support’s Sven by pushing upward on his skis perpendicular to the slope, and the friction between Sven’s skis and the snow points in the opposite direction from his motion. The work done by each of these forces can be determined using the dot product of the force and the displacement vector $\begin{array}{r}\stackrel{\to }{\mathrm{△}x}\end{array}$ .
  ::斯文的重量向下推向了地球的中心,雪力支撑的斯文(Sven)向上推向与斜坡垂直的滑雪滑雪滑雪台,以及斯文的滑雪台与雪点之间的摩擦与运动相反的方向。 这些力量所完成的工作可以用力量的圆点产物和移位矢量 x 来决定。

  播放段落

  $\begin{array}{r}W=\stackrel{\to }{F}\times \stackrel{\to }{\mathrm{△}x}=F(\mathrm{△}x)\text{cos}\theta \end{array}$
  ::W=F*x*F*F(x)cos _______________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  $\begin{array}{r}{W}_{friction}=\stackrel{\to }{F_{friction}}\times \stackrel{\to }{\mathrm{△}x}=(F_{friction})(\mathrm{△}x)\text{cos}{180}^{\circ }=-F_{friction}\mathrm{△}x\end{array}$
  ::Wfriction = Ffriction_x}( Ffriction (\\\\\\\\x) COs 180\\\Ffriction_x)

  播放段落

  $\begin{array}{r}{W}_{support}=\stackrel{\to }{F_{support}}\times \stackrel{\to }{\mathrm{△}x}=(F_{support})(\mathrm{△}x)\text{cos}{90}^{\circ }=0\end{array}$
  ::Wsupid=Fsupportx(Fsupid (x) cos 900

  播放段落

  $\begin{array}{r}{W}_{weight}=\stackrel{\to }{F_{weight}}\times \stackrel{\to }{\mathrm{△}x}=(F_{weight})(\mathrm{△}x)\text{cos}\theta =(F_{weight})(\mathrm{△}x)\text{sin}\varphi \end{array}$
  ::W重量=F重量=xxx(F重量=xx)cos *(F重量=xx) sin {_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Magnetic Force
  ::磁力

  播放段落

  The force that a magnetic field exerts on a charged particle is strongest when the particle moves perpendicular to the field and the magnetic force on the particle is equal to zero when it moves parallel to the field. Therefore the magnetic force can be described using the cross-product of the field strength vector and the particle’s velocity vector: $\begin{array}{r}\stackrel{\to }{F}=q\stackrel{\to }{v}\times \stackrel{\to }{B}\end{array}$ where $\begin{array}{r}\stackrel{\to }{F}\end{array}$ is the force on the particle, q is the charge of the particle, $\begin{array}{r}\stackrel{\to }{v}\end{array}$ is the velocity of the particle, and $\begin{array}{r}\stackrel{\to }{B}\end{array}$ is the vector representing the magnetic field. If the velocity is measured in m/s and if the magnetic field is measured in tesla, the force will be measured in newtons, the metric base-unit of force.
  ::磁场对充电粒子施加的最强力是粒子对地的垂直移动,而粒子的磁力在与场平行移动时等于零。因此,磁力可以用场强度矢量和粒子速度矢量的交叉产品来描述:FqvB是粒子的力,q是粒子的电荷,v是粒子的速率,B是代表磁场的矢量。如果以 m/s测量速度,如果磁场以特斯拉测量,那么力将用牛顿测量,即强度的公吨。

  播放段落

  Torque
  ::托盘

  播放段落

  When you lift a baseball off a table-top, you are exerting a force that moves the object as a whole. When you apply a force to a doorknob, you cause the door to rotate on its hinges. Scientists use the term torque to describe the force-like property that affects the rotation of an object. The torque can be described using the cross-product of the force vector and the lever arm, a vector pointing radially outward from the axis of rotation to the point where the force is applied to the object: $\begin{array}{r}\stackrel{\to }{\tau }=\stackrel{\to }{r}\times \stackrel{\to }{F}\end{array}$ , where $\begin{array}{r}\stackrel{\to }{\tau }\end{array}$ is the torque, $\begin{array}{r}\stackrel{\to }{r}\end{array}$ is the lever arm, and $\begin{array}{r}\stackrel{\to }{F}\end{array}$ is the applied force.
  ::当您将棒球从桌面上举起时,您正在施压将物体整体移动。当您对门把手施压时,您会让门在门把手上旋转。 科学家使用“ 托克” 一词来描述影响物体旋转的类似力的属性。 托克可以使用“ 托克” 和“ 杠杆臂” 的交叉产物来描述。 托克从旋转轴向外直直直指到“ rF” ,“ 托克” 是“ 托克” , “ r ” 是“ 杠杆臂” , F是应用力 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

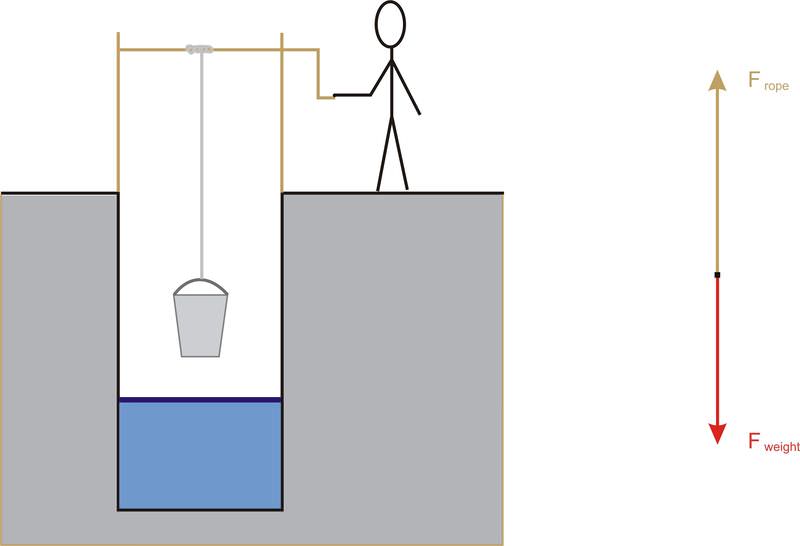
  播放段落

  Xiao turns a crank to lower a bucket of water into a well. Determine the total work done on the bucket if the weight of the bucket is 15 N and the tension force in the rope is 13 N. The bucket rises a distance of 4.5 m while he is cranking.
  ::Xiao把一个曲柄把一桶水降为一口井。如果桶的重量为15牛顿,绳子的紧张力为13牛顿,确定桶上完成的全部工作。 当他转动时,桶子上升的距离为4.5米。

  

  播放段落

  The work done by a force acting on an object is described by the dot product of the force vector and the displacement vector: $\begin{array}{r}W=\stackrel{\to }{F}\times \stackrel{\to }{\mathrm{△}x}=F(\mathrm{△}x)\text{cos}\theta \end{array}$ . In this case, the rope does negative work on the bucket because the motion and the force are in opposite directions. If the force is measured in newtons and the displacement in meters, the work is measured in Joules.
  ::在物体上发挥作用的一股力量所完成的工程由力量矢量和移位矢量的点产物W=FxF(x)(x)cs * 来描述。在这种情况下,绳子在桶上做负工作,因为运动和力向相反的方向。如果用牛顿和米的移位测量力,则用Joules测量工作。

  播放段落

  $\begin{array}{r}{W}_{rope}=\stackrel{\to }{F_{rope}}\times \stackrel{\to }{\mathrm{△}x}=F_{rope}(\mathrm{△}x)\text{cos}\theta =(13N)(4.5m)\text{cos}{180}^{\circ }=-58.5J\end{array}$
  ::Wrope=FropexFrope (x) cos (13N)(4.5m) cos 18058.5J

  播放段落

  The weight force does positive work on the bucket because the motion and the force are in the same direction.
  ::重量力在桶上确实起到了积极作用,因为运动和力是朝着同一方向前进的。

  播放段落

  $\begin{array}{r}{W}_{weight}=\stackrel{\to }{F_{weight}}\times \stackrel{\to }{\mathrm{△}x}=F_{weight}(\mathrm{△}x)\text{cos}\theta =(15N)(4.5m)\text{cos}{0}^{\circ }=\end{array}$ $\begin{array}{r}67.5J\end{array}$
  ::W重量=F重量=F重量=x重量=F重量==F重量=F重量==F重量==F重量==F重量==F重量==F重量==F重量=F重量=F重量=x)cos *===(15N)(4.5m)cs 0=67.5J

  播放段落

  The total work is the sum of the two individual amounts of work.
  ::总工作量是两种单项工作量的总和。

  播放段落

  $\begin{array}{r}{W}_{total}=W_{rope}+W_{weight}=-58.5+67.5J=9.0J\end{array}$
  ::W总计=作物+体重58.5+67.5J=9.0J

  播放段落

  A total of 9.0 J of work is done on the bucket as the bucket moves downward into the well.
  ::随着桶向下进入井中,在桶上总共做了9.0焦耳的工作。

  播放段落

  Example 2
  ::例2

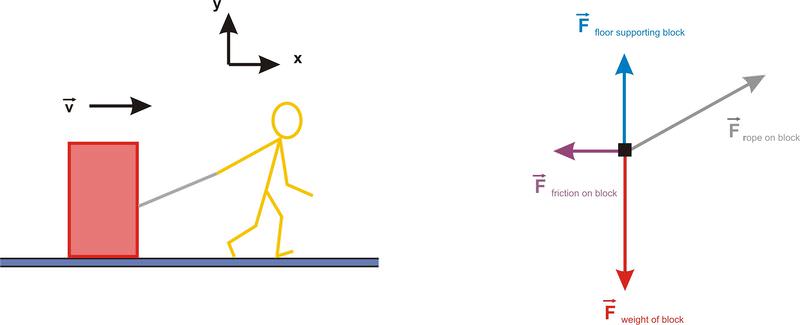
  播放段落

  The diagram below shows Sanjay pulling a large crate across the floor. The four forces which act on the crate during this process are shown in the diagram below. Which of the four forces exert non-zero force on the crate?
  ::下图显示Sanjay在地板上拉着一个大箱子。在此过程中在箱子上行动的四支力量如下图所示。这四支力量中的哪支在箱子上施加了非零力?

  

  播放段落

  The dot product is defined by $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|A||B|\text{cos}\theta \end{array}$ therefore only forces which have at least some component parallel to the motion will do non-zero work on the object. The angle θ between the displacement and forces perpendicular to the motion is 90 ^o so $\begin{array}{r}\stackrel{\to }{A}\times \stackrel{\to }{B}=|A||B|\text{cos}\theta =0\end{array}$ . The force from the floor and the weight of the crate do no work, since both of these forces are perpendicular to the motion of the crate. The rope does positive work on the crate since the force of the rope on the crate has a non-zero x-component. The friction does negative work on the crate since it is in the opposite direction from the displacement.
  ::圆点产品由 ABABBCC BAABBB BBBBB

  播放段落

  Example 3
  ::例3

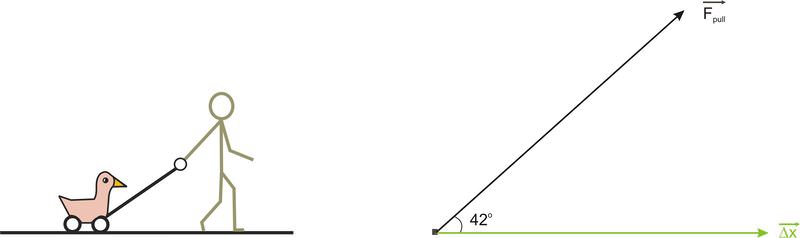
  播放段落

  De’andra is pulling her toy duck (mass 0.75 kg) at a constant speed of 3.0 m/s. The string she uses to pull the duck makes an angle of 42 ^o above the horizontal and De’andra keeps a constant tension in the string of 2.0 N. What is the amount of work done by the tension force when the duck is pulled forward a distance of 2.8 m?
  ::Deandra正以3.0米/秒的恒定速度拉起她的玩具鸭(0.75公斤)。她用来拉鸭的绳子的角是水平的42o,而Deandra在2.0牛身的绳子上保持了恒定的紧张。 当鸭子被拉到2.8米的距离时,紧张力量完成的工作量是多少?

  

  播放段落

  The work done by De’andra on the duck depends on the force she uses to pull the duck and on the distance the duck moves while she pulls. It also depends on the angle between the pulling force and the displacement vector.
  ::Deandra对鸭子的工作取决于她拉鸭子所使用的力以及鸭子拉动时的距离。 这还取决于拉动力和移位矢量之间的角。

  播放段落

  $\begin{array}{r}\stackrel{\to }{F_{pull}}\times \stackrel{\to }{x}=|\stackrel{\to }{F_{pull}}||\stackrel{\to }{x}|\text{cos}\theta =(2.0N)(2.8m)\text{cos}{42}^{\circ }=4.16Nm\end{array}$
  ::FpullxFpullxcos(2.0N)(2.8m) com 424.16Nm

  播放段落

  The N represents “newton”, the unit of force. The m represents “meters,” the unit of displacement. (1.0 N)(1.0 m) = 1.0 J where J represents “joules,” the unit of work and energy.
  ::N表示“牛顿”,即武力单位,m表示“米”,即流离失所单位。 (1.0N(1.0m)=1.0J,J表示“焦耳”,即工作单位和能量单位。)

  播放段落

  Example 4
  ::例4

  播放段落

  Beuford has once again taken Brynna to the park to play on the slide. If Brynna has a weight of 25 kg and if the slide has a 30 ^o incline above the horizontal, what work is done by her weight as she slides down the 3.5 m incline? Remember that the weight force in newtons is equal to the product of the mass and the acceleration of gravity, 9.8 m/s ² .
  ::Beuford再次将Brynna带到公园播放幻灯片。如果Brynna的重量为25公斤,如果幻灯片在水平上方有30摄氏线,那么在她滑下3.5米摄氏线时,她的重量会做什么工作?记住牛顿的重量力相当于质量和重力加速的产物,9.8 m/s2。

  

  播放段落

  If the slide is inclined at 30 ^o above the horizontal, then θ = 60 ^o from the vertical. The work done by a force on an object is given by the dot product of the force and the displacement of the object. Here $\begin{array}{r}\stackrel{\to }{F_{weight}}=mg=(25kg)(9.8m/s^2)=245N\end{array}$ . Therefore,
  ::如果幻灯片的倾角为水平上方30o, 则 = = 60o, 则从垂直 = = = 60o。 物体上的力所完成的工作由物体的点产物和物体的移位提供。 这里的 Fxight\ mg=( 25kg)( 9. 8m/ s2) = 245N。 因此,

  播放段落

  $\begin{array}{r}W=\stackrel{\to }{F_{weight}}\times \stackrel{\to }{d}=|\stackrel{\to }{F_{weight}}||\stackrel{\to }{d}|\text{cos}\theta =(245N)(3.5m)\text{cos}{60}^{\circ }=428.75J\end{array}$
  ::W=F重量=F重量=F重量=F重量=F重量=D重量=Cos=(245N(3.5m)cs 60428.75J)

  播放段落

  Example 5
  ::例5

  播放段落

  The scientists at Fermi Lab in Chicago, IL use magnetic fields to direct beams of protons during their explorations of the submicroscopic structure of atoms and quarks. Both magnetic field strength and the velocity of the protons are vector quantities. Determine the force on a proton moving northward at 4.2 × 10 ⁶ m/s through a magnetic field of 2.5 T oriented from east to west. (Note: protons are very tiny and are therefore able to move VERY fast.)
  ::芝加哥Fermi实验室的科学家们在探索原子和夸克亚微微微层结构时,IL利用磁场引导质子束。磁场强度和质子速度都是矢量。确定质子上向北移动的强度为4.2×106米/秒,从东向西移动为2.5T的磁场。 (注意:质子非常小,因此移动速度非常快。 )

  播放段落

  Define a coordinate system where eastward is the +z direction, northward is the +y direction, and upward is the +z direction. In this coordinate system, $\begin{array}{r}\stackrel{\to }{v}=⟨0,4.2\times {10}^6,0⟩\end{array}$ and $\begin{array}{r}\stackrel{\to }{B}=⟨-2.5,0,0⟩\end{array}$ . Therefore, $\begin{array}{r}|\stackrel{\to }{F}|=q|\stackrel{\to }{v}\times \stackrel{\to }{B}|=q\left(|\stackrel{\to }{v}||\stackrel{\to }{B}|\text{sin}\theta \right)\end{array}$ . Since the velocity is northward and the magnetic field is westward, the angle between the two vectors is 90 ^o .
  ::定义一个坐标系统, 向东是 +z 方向, 向北是 +y 方向, 向上是 +z 方向。 在这个坐标系统中, v0, 42x106, 0 和 B2.5, 0, 0。 因此, FqvBq (vBsin ) 。 由于速度向北, 磁场向西, 两个矢量之间的角是 90 。

  播放段落

  $\begin{array}{r}|\stackrel{\to }{F}|=q|\stackrel{\to }{v}\times \stackrel{\to }{B}|=q\left(|\stackrel{\to }{v}||\stackrel{\to }{B}|\text{sin}\theta \right)=(1.6\times {10}^{-19})\left((4.2\times {10}^6)(2.5)\text{sin}{90}^{\circ }\right)=\end{array}$ $\begin{array}{r}16.8\times {10}^{-13}N\end{array}$
  ::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  Using the right-hand-rule, we can determine the direction of the force on the proton. If you point your thumb northward along the velocity vector and your fore-finger westward along the magnetic field vector, your palm and your extended middle-finger point upward. Therefore the force which the magnetic field exerts on the proton is in the +z direction: $\begin{array}{r}|\stackrel{\to }{F}|=q\stackrel{\to }{v}\times \stackrel{\to }{B}=⟨0,0,16.8\times {10}^{-13}N⟩\end{array}$ .
  ::使用右手法则, 我们可以确定质子上的力的方向。 如果您用拇指向北指向速度矢量和前指向西指向磁场矢量、 手掌和伸展的中指点向上。 因此, 质子上磁场所施加的力在 +z 方向 : @FqvB0, 0, 16.8×10- 13N 。 @ fqvB0, 0, 16.8×13N 。

  播放段落

  Example 6
  ::例6

  播放段落

  If two children, Rudolfo (weight = 210 N) and Jennifer (weight = 175 N), sit on either end of a see-saw as shown below. Rudolfo is 1.0 m from the pivot and Jennifer is 1.4 m from the pivot. What torques are exerted by the children on the see-saw?
  ::如果Rudolfo(重量=210 N)和Jennifer(重量=175 N)这两个孩子坐在下文所示的锯锯两端,Rudolfo在支流上为1.0米,Jennifer在支流上为1.4米。

  

  播放段落

  The coordinate system has been defined such that the weight-force vectors are parallel to the y-axis and the lever-arm vectors are parallel to the x-axis. First determine the component form of each vector equation and then use the component version of the cross-product equation to determine the torque exerted by each child.
  ::坐标系统的定义是,重量力矢量与 Y 轴平行,杠杆-手臂矢量与 x 轴平行。首先确定每个矢量方程式的组件形式,然后使用跨产品方程式的组件版本来确定每个孩子的托盘。

  播放段落

  $\begin{array}{r}\stackrel{\to }{{\tau }_R}=\stackrel{\to }{r_R}\times \stackrel{\to }{F_{weight,R}}=⟨-1.0m,0,0⟩\times ⟨0,-210N,0⟩\end{array}$
  ::RrF重量,R1.0m,0,00,2-210N,0

  播放段落

  $\begin{array}{r}\stackrel{\to }{r}\times \stackrel{\to }{F}=⟨(r_y{F}_z-r_z{F}_y),(r_z{F}_x-r_x{F}_z),(r_x{F}_y-r_y{F}_x)⟩\end{array}$
  ::rF(ryFz-rzFy),(rzFx-rxFz),(rxFy-ryFx)

  播放段落

  $\begin{array}{r}\stackrel{\to }{r_R}\times \stackrel{\to }{F_R}=⟨\left((0\ast 0)-(0\ast -210)\right),\left((0\ast 0)-(-1\ast 0)\right),\left((-1\ast -210)-(0\ast 0)\right)⟩=\end{array}$ $\begin{array}{r}⟨0,0,210mN⟩\end{array}$
  ::rRFR(00)-(0210),(00)-(10)),((1210)-(00),0,210mN

  播放段落

  $\begin{array}{r}\stackrel{\to }{{\tau }_J}=\stackrel{\to }{r_J}\times \stackrel{\to }{F_{weight,J}}=⟨1.4m,0,0⟩\times ⟨0,-170N,0⟩\end{array}$
  ::JrJF重量,J140m,0,00,-170N,00

  播放段落

  $\begin{array}{r}\stackrel{\to }{r}\times \stackrel{\to }{F}=⟨(r_y{F}_z-r_z{F}_y),(r_z{F}_x-r_x{F}_z),(r_x{F}_y-r_y{F}_x)⟩\end{array}$
  ::rF(ryFz-rzFy),(rzFx-rxFz),(rxFy-ryFx)

  播放段落

  $\begin{array}{r}\stackrel{\to }{r_J}\times \stackrel{\to }{F_J}=⟨\left((0\ast 0)-(0\ast -170)\right),\left((0\ast 0)-(1.4\ast 0)\right),\left((1.4\ast -170)-(0\ast 0)\right)⟩=\end{array}$ $\begin{array}{r}⟨0,0,-238mN⟩\end{array}$
  :0*0)-(0*170),(0*0)-(1.4*0),(14*170)-(0*0),(0}0,0,-238mN)

  播放段落

  Example 7
  ::例7

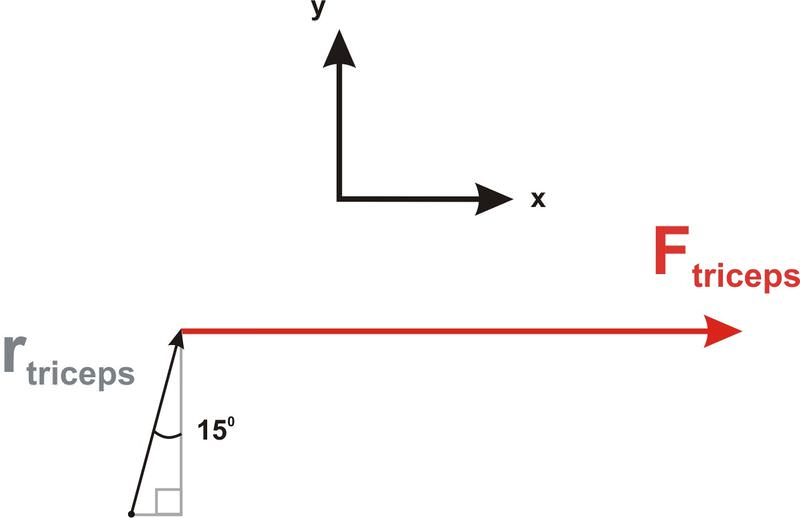
  播放段落

  Exercise scientists and physical therapists use torque to analyze various exercises such as the triceps exercise shown in the diagram below. Here, the triceps muscle exerts a force on the elbow-end of the forearm, affecting the rotation of the forearm. If the triceps exerts a force of 17 N, what torque is applied to the forearm?
  ::运动科学家和物理治疗师用硬力分析各种练习,例如下图所示的三环运动。这里,三环肌肉在前臂肘端施加力力,影响前臂的旋转。如果三环施加力为17N,对前臂施用什么力?

  

  播放段落

  Since the forearm is positioned at an angle of 15 ^o to the vertical, the angle between the two vectors is 90 ^o – 15 ^o = 75 ^o . The magnitude of the lever-arm vector is the distance from the elbow-pivot to the point where the triceps pulls on the bone, $\begin{array}{r}|\stackrel{\to }{r}|=2.5cm\end{array}$ . Similarly, the magnitude of the force vector is the strength of the force, $\begin{array}{r}|\stackrel{\to }{F}|=17N\end{array}$ . Since we know the magnitudes of both vectors and the angle between them, we can use the angle-version of the cross-product equation to determine the magnitude of the torque.
  ::由于前臂位于15o到垂直角的角上, 两个矢量之间的角是 90o - 15o = 75o。 杠杆- 手臂矢量的大小是从肘- pivot 到三角拉到骨头的距离, r\\\\ 2.5cm。 同样, 力矢量的大小是力的强度, F17N。 由于我们了解两个矢量的大小以及它们之间的角, 我们可以使用交叉产品方程的角转换来确定托盘的大小 。

  播放段落

  $\begin{array}{r}|\stackrel{\to }{\tau }|=rF\text{sin}\theta =(2.5cm)(17N)\text{sin}75=41.05cm\cdot N\end{array}$
  ::*rF sin * (2.5cm(17N)) sin 75=41.05cmN*

  播放段落

  Review
  ::回顾

  播放段落
  1. A fishing boat sails due west at a constant 15 km/h. A current of 3 km/h is running due south. What is the velocity of the boat relative the sea floor?
     ::一艘渔船在西面以恒定的每小时15公里处航行。 3公里/小时的洋流正向南流。 该船的速度与海底相比是多少?
  播放段落
  2. Two bulldozers pull on a large tree to move it out of the way of a road. One bulldozer pulls 3000N west and the other bulldozer 2500N in a southerly direction because of the terrain. Determine the resultant force acting on the tree. If the tree has a mass of 1000 kg calculate the acceleration of the tree due to the resultant force acting on it.
     ::两辆推土机拉着一棵大树,将树从一条道路的道路上移开,一辆推土机从西3 000N向南拉动,另一辆推土机从南方向2 500N,确定树上随后的动力,如果树上的动力为1000公斤,则计算树上因动力而加速的树速。
  播放段落
  3. Three coplanar horizontal forces each of magnitude 10 N act on a body of mass 5 kg. Determine the magnitude of the net force acting on the body and the magnitude of the resultant acceleration.
     ::3个共平面水平力,每个10N级,对一个质量为5千克的物体采取行动。确定对体净力的大小和由此加速的程度。
  播放段落
  4. If vector A = 5 N north and vector B = 10 N east, find the resultant of vector A – vector B.
     ::如果矢量A = 5 N 北纬5 N 和矢量B = 10 N 东经10 N,则发现矢量A - 矢量B的产物。
  播放段落
  5. A submarine is travelling at 20 km/h due east. Shortly after, it is travelling due north at 15 km/h. Calculate the change in velocity.
     ::一艘潜艇正向东行驶20公里/小时,随后不久向北行驶15公里/小时。 计算速度的变化。
  播放段落
  6. An fighter jet has a true airspeed of 1000 km/h due east. There is a cross wind blowing 60 degrees east of south at 100 km/h. Calculate the velocity of the jet relative to the ground.
     ::一架战斗机的飞行速度为每小时1000公里/小时,向东飞来,横风向南以东60度,每小时100公里/小时。 计算喷气飞机相对于地面的速度。
  播放段落
  7. A pallet of mass 10 kg sits on a horizontal surface, a force is exerted on the pallet by means of a chain inclined at 60° to the horizontal. If the tension in the chain is 150 N and the frictional force between the pallet and the horizontal surface is 55 N, will the pallet move under these conditions? Explain. If the pallet does move determine the size of the acceleration with which it moves.
     ::10公斤质量的托盘坐落在水平表面,通过一个在60°向水平倾斜的链条对托盘施加了力量。如果链条的紧张度为150牛顿,托盘与水平表面之间的摩擦力为55牛顿,托盘在这些条件下会移动吗?解释。如果托盘确实移动决定其移动的加速度大小。
  播放段落
  8. A broken down car with a total mass of 300 kg is pulled by a single tow line attached to a tow-truck with a mass of 1000 kg. If the drag on the truck and the car is one-tenth of their respective weights, and the total forward force exerted by the tow-truck is 5130 kg force (ie 5130 x 9.8 N), find the magnitude of: a. the total force resisting the forward motion of the truck and car; b. the acceleration of the truck/car system; c. the unbalanced accelerating force on the broken down car; d. the tension in the towing line.
     ::一辆总重量为300公斤的破碎汽车由一条连接拖车-拖车-拖车-拖车-总重量为1000公斤的单拖线拉扯,如果卡车和汽车拖拉力是其各自重量的十分之一,拖车-拖车总向前力为5130公斤(即5130x9.8N),则发现以下强度:a. 抵抗卡车和汽车前向运动的总力;b. 卡车/车系统的加速;c. 破损汽车的加速力不平衡;d. 拖车线的紧张。
  播放段落
  9. A fighter pilot with a mass of MA = 80 kg sits in the cock-pit with his back horizontal to the ground. His jet is moving vertically with acceleration a. If the acceleration due to gravity on the pilot is g = 9.8 ms-2, write a mathematical expression for and calculate the value of the reaction force R between the pilot and the back of his seat in the jet when: a. a = 0; b. a = 8 ms-2 upwards; c. a = 8 ms-2 downwards.
     ::a. a. a = 0; b. a = 8 ms-2 向上; c. a = 8 ms-2 向下。
  播放段落
  10. A plane is flying 691mph headed 13° east of north. A tail wind is blowing 67° west of north at 92 mph. Determine the actual speed of the plane relative the ground.
      ::一架飞机向北13度以东飞行691厘米,尾风向北67度以92米以西吹,确定飞机的实际速度与地面相对应。
  播放段落
  11. A UFO is gliding along at 516 mph, headed 32° east of south. Determine the direction of the UFO if the wind is blowing 42° west of north at 29 mph.
      ::UFO在516米时正在滑行,向南以东32度,确定UFO的方向,如果风向在29米时向北以西42度吹,则确定UFO的方向。
  播放段落
  12. A rocket is flying 63° west of north at 575 mph. Determine the actual direction of the rocket if the wind is blowing 22° west of south at 78 mph.
      ::一枚火箭在北纬63度以西575英里处飞行,如果风吹向南纬22度以西78英里处,确定火箭的实际方向。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。