Course: 7.9 精度几何系列的总数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

精度几何系列总和

Anna is on a progressive workout plan, so every day she adds 5% to her exercise time. If she starts by exercising 15 mins on the first day, how many minutes will she have exercised all together on day 45?
::安娜在逐步健身计划上,所以她每天的锻炼时间增加5%。如果她在第一天以锻炼15分钟开始,她第45天会一起锻炼多少分钟?

This is a geometric series, since the difference between the exercise time on any two days is greater than the difference between any prior two days. You could just add: $\begin{aligned} 15 + (15 \cdot 1.05) + [(15 \cdot 1.05) \cdot 1.05] . . . \end{aligned}$ and so on up to 45, but that would be horribly tedious. In this lesson, you will learn how to answer a question like this will little effort.
::这是一个几何序列, 因为任何两天的练习时间之间的差大于前两天的差。您可以添加: 15+( 15_ 1. 05) +[ (15_ 1. 05. 05) +[ (15_ 1. 055) + [ (15_ 1. 05. 1.05) +... 等, 最多45 个, 但这会非常无聊。在这个教训中, 您将学习如何回答这样的问题, 这样的努力是微不足道的。

Sums of Finite Geometric Series
::精度几何系列总和

A finite geometric series is simply a geometric series with a specific number of terms. For example, consider the series: 50 + 25 + 12.5 + ....The series is geometric: the first term is 50, and the common ration is (1/2).
::限定几何序列只是一个带有若干具体术语的几何序列,例如,考虑该序列:50+25+12.5+......。该序列是几何序列:第一个术语是50,共同配给(1/2)。

The sum of the first two terms is 50 + 25 = 75. We can write this as S ₂ = 75
::前两个任期的总和是50+25=75,我们可以写成S2=75

The sum of the first three is 50 + 25 + 12.5 = 87.5. We can write this as S ₃ = 87.5
::前三个加50+25+12.5=87.5。我们可以把它写成S3=87.5。

To find the value of S _n in general, we could simply add together the first n terms in a series. However, this would obviously be tedious for a large value of n . Given the regular pattern in a geometric series - every term is (1/ r ) of the previous term, and the n ^th term is a _n = a ₁ r ^{n - 1} , we can use induction to prove a formula for S _n .
::为了找到一般的SN值,我们可以简单地在一系列中将第一个 n 术语加在一起。然而,这显然对一个 n 的较大值是乏味的。鉴于几何序列中的常规模式-每个术语都是上一术语的1/r, 而 n 术语是 = a1n - 1, 我们可以用感应来证明 Sn 的公式。

The sum of the first n terms in a geometric series is $\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} \end{aligned}$
::几何序列中第一个 n 术语的总和是 Sn=a1( 1- rn) 1-r

For example, for the series 50 + 25 + 12.5 + ... , the sum of the first 6 terms is:
::例如,在50+25+12.5+...系列中,前6个术语的总和是:

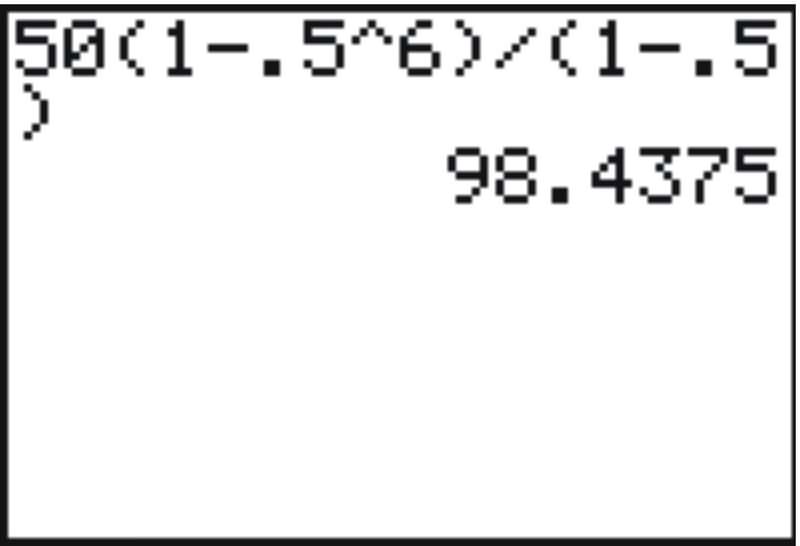
$\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} = \frac{50 (1 - (\frac{1}{2})^{6})}{1 - \frac{1}{2}} = \frac{50 (1 - \frac{1}{64})}{\frac{1}{2}} = \frac{50 (\frac{63}{64})}{\frac{1}{2}} = 50 (\frac{63}{64}) (\frac{2}{1}) = 98 \frac{7}{16} \end{aligned}$
::Sn=a1(1-rn)1-r=50(1-(126)1-12=50(1-164)12=50(6364)12=50(6364)(21)=98716

The figure below shows the same calculation on a TI-83/4 calculator:
::下图显示对TI-83/4计算器的计算结果相同:

We can use this formula as long as the series in question is geometric.
::只要有关序列是几何数,我们就可以使用这个公式。

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about Anna and her progressive workout plan.
::之前有人问过你安娜和她的累进疗养计划

Every day she adds 5% to her exercise time. If she starts by exercising 15 mins on the first day, how many minutes will she have exercised all together on day 45?
::她每天的锻炼时间增加5%,如果第一天她以锻炼15分钟开始,第45天她将一起锻炼多少分钟?

Use the formula: $\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} \end{aligned}$
::使用公式: Sn=a1 (1-rn)1-r

$\begin{aligned} S_{n} = \frac{15 (1 - {1.05}^{45})}{1 - 1.05} \end{aligned}$
::Sn=15(1-1.05451-1.05)

$\begin{aligned} S_{n} = 2395.5 \end{aligned}$ minutes.
::Sn=2395.5分钟。

Example 2
::例2

Find the sum of the first 10 terms of a geometric series with a ₁ = 3 and r = 5.
::查找几何序列中前10个条件的a1 = 3和r = 5的总和。

The sum is 58,593.
::合计58 593美元。

$\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} = \frac{3 (1 - 5^{7})}{1 - 5} = \frac{3 (1 - 78, 125)}{- 4} = \frac{3 (- 78, 124)}{- 4} = 58, 593 \end{aligned}$
::Sn=a1(1-rn)1-r=3(1-57)1-5=3(1-78,125)-4=3(-78,124)-4=58,593

Notice that because the common ratio in this series is 5, the terms get larger and larger. This means that for increasing values of n the sums will also get larger and larger. In contrast, in the series with common ratio (1/2), the terms gets smaller and smaller. This situation implies something important about the sum.
::请注意, 由于这个系列中的通用比率是 5, 条件会越来越大。这意味着对于增加的 n 值来说, 总额也会越来越大。相反, 在具有通用比率(1/2)的序列中, 条件会越来越小。这种情况意味着总和的重要性。

Example 3
::例3

Find the sum of each series:
::查找每个序列的总和 :

The first term of a geometric series is 4, and the common ratio is 3. Find S ₈ .
::几何序列的第一个任期是4,共同比率是3. 查找S8。

$\begin{aligned} S_{8} = \frac{4 (1 - 3^{8})}{1 - 3} = 13, 120 \end{aligned}$
::S8=4(1-38)1-3=13,120

The first term of a geometric series is 80, and the common ratio is (1/4). Find S ₇ .
::几何序列的第一个任期为80,共同比率为1/4。

$\begin{aligned} S_{7} = \frac{80 (1 - {(\frac{1}{4})}^{7})}{1 - \frac{1}{4}} \approx 106.66 \end{aligned}$
::S7=80(1-(147)1-14106.66

Example 4
::例4

Prove the formula $\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} \end{aligned}$ by induction.
::通过诱导证明公式Sn=a1(1-rn)1-r。

Step 1) If n = 1, the n ^th sum is the first sum, or a ₁ . Using the hypothesized equation, we get $\begin{aligned} S_{1} = \frac{a_{1} (1 - r^{1})}{1 - r} = \frac{a_{1} (1 - r)}{1 - r} = a_{1} \end{aligned}$ . This establishes the base case.
::步骤1 如果 n = 1, 则nth和为第一个和或a1。使用假设方程,我们得到S1=a1(1-r1)1-r=a1(1-r)1-r=a1。这确定了基数。

Step 2) Assume that the sum of the first k terms in a geometric series is $\begin{aligned} S_{k} = \frac{a_{1} (1 - r^{k})}{1 - r} \end{aligned}$ .
::第2步假设几何序列中第一个 k 术语的总和是 Sk=a1(1-rk)1-r。

Step 3) Show that the sum of the first k +1 terms in a geometric series is $\begin{aligned} S_{k + 1} = \frac{a_{1} (1 - r^{k + 1})}{1 - r} \end{aligned}$ .
::步骤3)显示几何序列中第一个 k+1 术语的总和是 Sk+1=a1(1- rk+1)1-r。

$\begin{aligned} S_{k + 1} = S_{k} + a_{k + 1} \end{aligned}$	The $\begin{aligned} k + 1 \end{aligned}$ sum is the $\begin{aligned} k^{t h} \end{aligned}$ sum, plus the $\begin{aligned} k + 1 \end{aligned}$ term
$\begin{aligned} = \frac{a_{1} (1 - r^{k})}{1 - r} + a_{1} r^{k + 1 - 1} \end{aligned}$	Substitute from step 2, and substitute the $\begin{aligned} k + 1 \end{aligned}$ term
$\begin{aligned} = \frac{a_{1} (1 - r^{k})}{1 - r} + \frac{a_{1} r^{k} (1 - r)}{1 - r} \end{aligned}$	The common denominator is $\begin{aligned} 1 - r \end{aligned}$
$\begin{aligned} = \frac{a_{1} (1 - r^{k}) + a_{1} r^{k} (1 - r)}{1 - r} \end{aligned}$	Simplify the fraction
$\begin{aligned} = \frac{a_{1} [1 - r^{k} + r^{k} (1 - r)]}{1 - r} \end{aligned}$
$\begin{aligned} = \frac{a_{1} [1 - r^{k} + r^{k} - r^{k + 1}]}{1 - r} \end{aligned}$
$\begin{aligned} = \frac{a_{1} [1 - r^{k + 1}]}{1 - r} \end{aligned}$	It is proven.

Therefore we have shown that $\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} \end{aligned}$ for a geometric series. Now we can use this equation to find any sum of a geometric series.
::因此,我们已经展示了 Sn=a1(1-rn)1-r 用于几何序列。现在我们可以使用这个方程来找到几何序列的任何数量。

Example 5
::例5

Find the sum: $\begin{aligned} 5 + 10 + 20 + . . . + 640 \end{aligned}$ (Hint: if a _n = 640 , what is n ?).
::查找总和: 5+10+20+...+640 (提示: 如果 = 640, 什么是 n?) 。

$\begin{aligned} S_{8} = \frac{5 (1 - 2^{8})}{1 - 2} = 1275 \end{aligned}$
::S8=5(1-28)1-2=1275

Example 6
::例6

Write the first 5 terms of the : $\begin{aligned} - 5 \cdot {\frac{3}{4}}^{n} \end{aligned}$ .
::写下前五个条款: - 534n。

Just do the multiplication for each term $\begin{aligned} n = 0 \to n = 4 \end{aligned}$
::只做每个术语的乘数 n=0n=4

$\begin{aligned} - 5 \cdot {\frac{3}{4}}^{0} \to - 5 \cdot 1 \to - 5 \end{aligned}$ ..... for $\begin{aligned} n = 0 \end{aligned}$
::- 5 = 0 = 0 = = 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

$\begin{aligned} - 5 \cdot {\frac{3}{4}}^{1} \to - 5 \cdot \frac{3}{4} \to - \frac{15}{4} \to - 3.75 \end{aligned}$ ..... for $\begin{aligned} n = 1 \end{aligned}$
::-5 -341 -534 -534 -154 -3.75 N=1

$\begin{aligned} - 5 \cdot {\frac{3}{4}}^{2} \to - 5 \cdot \frac{9}{16} \to - \frac{45}{16} \to - 2.8 \end{aligned}$ ..... for $\begin{aligned} n = 2 \end{aligned}$
::-5 -342 -5 -916 -4516 -2.8 N=2

$\begin{aligned} - 5 \cdot {\frac{3}{4}}^{3} \to - 5 \cdot \frac{27}{64} \to - \frac{135}{64} \to - 2.1 \end{aligned}$ ..... for $\begin{aligned} n = 3 \end{aligned}$
::-534352764135642.1.n=3

$\begin{aligned} - 5 \cdot {\frac{3}{4}}^{4} \to - 5 \cdot \frac{81}{256} \to - \frac{405}{256} \to - 1.6 \end{aligned}$ ..... for $\begin{aligned} n = 4 \end{aligned}$
::-53445812564052561.6.n=4

$\begin{aligned} ∴ \end{aligned}$ the first 5 terms are: $\begin{aligned} - 5, - 3.75, - 2.8, - 2.1, - 1.6 \end{aligned}$
::前5个学期为:-5,-3.75,-2.8,-2.1,-1.6。

Example 7
::例7

Write the 3rd, 4th, and 6th terms of: $\begin{aligned} (3)^{(\frac{n}{2})} \end{aligned}$ .
::撰写第3、第4和第6个条款3)(n2)项。

As with Example 6, just perform the operations on the indicated values of n :
::与例6一样,仅按 n 的表示值执行操作:

$\begin{aligned} 3^{\frac{3}{2}} \to \sqrt{3^{3}} \to \sqrt{27} \to 5.2 \end{aligned}$ ..... for $\begin{aligned} n = 3 \end{aligned}$
::3 = 3 = 333 = 27 = 5.2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

$\begin{aligned} 3^{\frac{4}{2}} \to 9 \end{aligned}$ ..... for $\begin{aligned} n = 4 \end{aligned}$
::N=4 = 342=9...

$\begin{aligned} 3^{\frac{6}{2}} \to 3^{3} \to 27 \end{aligned}$ ..... for $\begin{aligned} n = 6 \end{aligned}$
::362-33-27... n=6

$\begin{aligned} ∴ \end{aligned}$ the 3rd, 4th, and 6th terms are: $\begin{aligned} 5.2, 9, 27 \end{aligned}$
::第3、第4和第6个学期是: 5.2,9,27

Example 8
::例8

Find the sum of the series: $\begin{aligned} \sum_{n = 1}^{6} {(- \frac{3}{2})}^{n - 1} \end{aligned}$ .
::查找序列的总和:n=16(- 32)n-1。

We could calculate all of the values for $\begin{aligned} n = 1 \to 6 \end{aligned}$ and add them, getting:
::我们可以计算所有 n=16 的值, 并添加它们, 获取 :

$\begin{aligned} 1 + \frac{- 3}{2} + \frac{9}{4} + \frac{- 27}{8} + \frac{81}{16} + \frac{- 243}{32} = \frac{- 133}{32} \end{aligned}$

Or we can use the formula: $\begin{aligned} (\frac{1 - r^{k}}{1 - r}) \end{aligned}$
::或者我们可以使用公式( 1- rk1- r) 。

$\begin{aligned} (\frac{1 - {(\frac{- 3}{2})}^{6}}{1 - (\frac{- 3}{2})}) = \frac{- 133}{32} \end{aligned}$

Review
::回顾

Find the sum of the finite series. You may simply calculate the individual terms and add them, or you may use the formula: $\begin{aligned} S_{n} = \frac{a_{1} (1 - r^{n})}{1 - r} \end{aligned}$ .
::查找限制序列的总和。您可以简单地计算单个术语并添加它们, 或者使用公式: Sn=a1( 1-rn)1-r。

$\begin{aligned} 1 + (- \frac{1}{2}) + \frac{1}{4} + . . . + \frac{1}{64} \end{aligned}$
$\begin{aligned} - 6 + 12 - 24 + . . . - 6144 \end{aligned}$
$\begin{aligned} (- 4) + (- 12) + (- 36) + . . . + (- 2916) \end{aligned}$
$\begin{aligned} 9 + (- 45) + 225 + . . . + (- 17, 578, 125) \end{aligned}$

$\begin{aligned} \sum_{n = 1}^{5} - (2)^{n - 1} \end{aligned}$
:n)=15-(2)-(n-1)

$\begin{aligned} \sum_{n = 1}^{10} 6 {(\frac{1}{2})}^{n - 1} \end{aligned}$
::=1106 (12)n-1

$\begin{aligned} \sum_{n = 1}^{6} 8 \cdot 3^{n - 1} \end{aligned}$
::=1683n-1
$\begin{aligned} (- 5) + 10 + (- 20) + . . . + (- 1280) \end{aligned}$
$\begin{aligned} (- 9) + \frac{9}{2} + (- \frac{9}{4}) + . . . + (- \frac{9}{16}) \end{aligned}$

$\begin{aligned} \sum_{n = 1}^{9} 4 \cdot {(\frac{1}{2})}^{n - 1} \end{aligned}$
::=1944(12)-1

$\begin{aligned} \sum_{n = 1}^{10} 4 \cdot {(- \frac{2}{3})}^{n - 1} \end{aligned}$
::=1104}(-23-1)
$\begin{aligned} (- 3) + (- \frac{3}{2}) + (- \frac{3}{4}) + . . . + (- \frac{3}{1024}) \end{aligned}$

$\begin{aligned} \sum_{n = 1}^{11} - 9 \cdot (- 2)^{(n - 1)} \end{aligned}$
::=111-9(-2)(n-1)

$\begin{aligned} \sum_{n = 1}^{9} - 9 \cdot {(- \frac{5}{3})}^{n - 1} \end{aligned}$
::=19-9(-53)-1

$\begin{aligned} \sum_{n = 1}^{6} - 2 \cdot {(- \frac{5}{4})}^{n - 1} \end{aligned}$
::=16-2(-54-1)

$\begin{aligned} \sum_{n = 1}^{11} 8 \cdot {(- \frac{1}{3})}^{n - 1} \end{aligned}$
::=1118 (- 13- 13n-1)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

精度几何系列总和

Sums of Finite Geometric Series ::精度几何系列总和

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Review ::回顾

Review (Answers) ::回顾(答复)