Course: 5.2 几何平均值 | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 几几何平均值

Collapse Expand
几几何平均值
Suppose you were assigned to help evaluate the scoring from surveys given to students to choose the prom king at your high school prom. The survey asked the students to score the nominees on a five-point scale for each of four categories, on a twenty-five point scale for each of three categories, and on a thirty-five point scale for the last 4 categories.
::假设你被指派帮助评估学生在高中毕业舞会上选择舞会王的考试成绩。调查要求学生按四类中的每类五分位、三个类中的每类二十五分位、最后四类中的每类三十五分位,按五分位评分。

How could you average the total scores for each nominee without the scores of the higher point categories overshadowing the scores of the lower-point ones?
::如何平均每个被提名人的总分数? 高分的分数不会掩盖低分的分数?

Geometric Mean
::几几何平均值

The geometric mean (also known as the mean proportional ) is a method of finding the ‘middle’ value in a set that contains some values that are intrinsically more influential than others. The geometric mean takes into account the differences in proportion between values in different ranges.
::几何平均值(也称为平均比例)是一种方法,用以在包含某些内在比其他数值更有影响力的一组数值中找到“中值 ” 。几何平均值考虑到不同范围数值之间的比例差异。

To calculate the geometric mean of a set of data :
::计算一组数据的几何平均值:

Multiply the value of each member of the set by the next, as in $\begin{align*}x_1 \times x_2 \times x_3 \times x_4\end{align*}$ , etc.
::乘以下一组的每个成员的值, 如 x1x2xx3x4 等。

Find the $\begin{align*}n^{th}\end{align*}$ root of the product of the set values, where $\begin{align*}n\end{align*}$ is the number of values in the set
::查找设定值的产值的 nth 根, n 是集中的数值数

The $\begin{align*}n^{th}\end{align*}$ root of the product of the set values is the geometric mean of the set
::设定值的产值 nth 根是集的几何平均值

The mean proportional can also be described in a couple of ways using geometry:
::平均比例也可以用几何方式描述:

If you have a rectangle with side lengths $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ , then the side length of a square with area equal to the rectangle is the mean proportional of $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ .
::如果有一个边长a和b的矩形,则方形的侧长与矩形相等的区域是a和b的平均值比例。

Alternatively:
::或者:

Construct a semicircle with a diameter length of $\begin{align*}a+b\end{align*}$ and a perpendicular line from the diameter to the semicircle located at the intersection of $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ . The length of the perpendicular line is the geometric mean of $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ .
::构造直径长为a+b的半圆圈和直径至位于a和b交点的半圆圈的直径直径至半圆圈的直径直线和直径至半圆圈的直径直径直线。垂直直圆线的长度为a和b的几何平均值。

Finding the Value a Mean is Proportional to
::查找值平均值的成比例值

What is the mean proportional of $\begin{align*}x\end{align*}$ ?
::x的平均值比例是多少?

$\begin{aligned} x = {8, 12, 14, 6, 9, 15, 22, 7} \end{aligned}$
$\begin{align*}x=\{8, 12, 14, 6, 9, 15, 22, 7\}\end{align*}$
::X8,12,14,6,9,9,15,22,7}

First find the product of the members of the set:
::首先找到集成成成份的产物:

$\begin{aligned} 8 \times 12 \times 14 \times 6 \times 9 \times 15 \times 22 \times 7 = 167, 650, 560 \end{aligned}$
$\begin{align*}8 \times 12 \times 14 \times 6 \times 9 \times 15 \times 22 \times 7=167, 650, 560\end{align*}$

Now take the 8 ^th root of the product (since there are 8 members in the set):
::现在选择产品的第8根根(因为集中有8个成员):

$\begin{aligned} \sqrt[8]{167, 650, 650} \approx 10.667 \end{aligned}$
$\begin{align*}\sqrt[8]{167, 650, 650} \approx 10.667\end{align*}$

Finding Unknown Values
::查找未知值

Ken has a dog kennel in back of his house. The dimensions of the kennel are 9 feet by 13 feet. What would be the side lengths of a square kennel enclosing the same area? What is another name for this value?
::Ken家后面有一条狗狗狗狗。狗狗的尺寸是9英尺乘13英尺。在同一个区域内,方格狗狗的侧长是多少?这个价值又叫什么?

First find the area of the original kennel:
::首先找到原始狗窝的面积 :

$\begin{aligned} 9 f t \times 13 f t = 117 f t^{2} \end{aligned}$
$\begin{align*}9 \ ft \times 13 \ ft= 117 \ ft^2\end{align*}$
::9英尺×13英尺=117英尺2

Now find the lengths of the sides of the square:
::现在找到广场两侧的长度:

$\begin{aligned} \sqrt{117 f t^{2}} = 10.82 f t \end{aligned}$
$\begin{align*}\sqrt{117 \ ft^2}=10.82 \ ft\end{align*}$
::117英尺2=10.82英尺

10.82 is the geometric mean of 9 and 13.
::10.82是9和13的几何平均值。

Finding the Average Rate of Return
::寻找平均回报率

Assume that $5000 was invested at a starting interest rate of 7%, and the rate increased by 2% each year for years 2, 3, 4, and 5 then decreased by 3% for year 6. What would the average rate of return be for the whole period?
::假设5 000美元投资的起始利率为7%,而第2、3、4和5年的利率每年增加2%,然后第6年减少3%。整个期间的平均收益率是多少?

It may seem that you could simply calculate the arithmetic mean of the interest rates to find the average yearly return. However, the arithmetic mean of the 6 yearly rates would only describe the average of the stated percentages each year. The complication is that a 7% interest rate in the first year would only result in 107% of the initial value, whereas a 7% rate in the 6 ^th year would yield 107% of the initial investment plus 107% of all of the interest from the prior years! Therefore, a different ‘middle number’ is needed.
::似乎你可以简单地计算利率的算术平均值以找到平均年回报率。但是,6年利率的算术平均值只能描述每年申报百分比的平均值。复杂的是,第一年7%的利率只能产生初始值的107 % , 而6年7%的利率将产生初始投资的107 % , 加上前几年的全部利息的107 % 。因此,需要有一个不同的“中数 ” 。

The geometric mean of the interest rates would provide the correct average yearly rate. We need to find the product of all of the yearly rates, and then take the 6 ^th root (since there are 6 rates in this problem) of that product. The correct calculation looks like this:
::利率的几何平均值可以提供正确的平均年利率。我们需要找到所有年利率的产物, 然后取出该产品的第六根( 因为这个问题有6个利率 ) 。正确的计算方法是这样的:

$\begin{aligned} \sqrt[6]{1.07 \times 1.09 \times 1.11 \times 1.13 \times 1.15 \times 1.12} = \sqrt[6]{1.88} = 1.11 \\ ∴ T h e a v e r a g e r e t u r n i s 11 % p e r y e a r \end{aligned}$
$\begin{align*}& \sqrt[6]{1.07 \times 1.09 \times 1.11 \times 1.13 \times 1.15 \times 1.12} = \sqrt[6]{1.88}=1.11 \\ & \qquad \quad \therefore \ The \ average \ return \ is \ 11\% \ per \ year\end{align*}$
::1.07x1.09x1.11x1.13x1.15x1.126=1.886=1.11* 平均回报率为每年11%

Earlier Problem Revisited
::重审先前的问题

Suppose you were assigned to help evaluate the scoring from surveys given to students to choose the prom king at your high school prom. The survey asked the students to score the nominees on a five-point scale for each of four categories, on a twenty-five point scale for each of three categories, and on a thirty-five point scale for the last 4 categories.
::假设你被指派帮助评估学生在高中毕业舞会上选择舞会王的考试成绩。调查要求学生按四类中的每类五分位、三个类中的每类二十五分位、最后四类中的每类三十五分位,按五分位评分。

How could you average the overall scores for each nominee without the disproportionate weighting that would occur in favor of the higher point categories if you used an arithmetic mean?
::如果使用算术平均值,如何在不出现偏重于较高分数类别的情况下,平均每个被提名人的总分数?

By calculating the geometric mean of the scores earned in all 11 categories, you could identify an average score for each contestant that was proportionately weighted based on category value.
::通过计算所有11个类别所得得分的几何平均值,你可以为每个参赛者确定一个根据类别价值按比例加权的平均得分。

Examples
::实例

Example 1
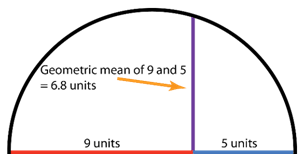
::例1

Construct a semicircular representation of the mean proportional of the values 5 and 9.
::构造值 5 和 9 的平均比例的半圆形表示数。

Use the geometric method described above: length $\begin{align*}a=9\end{align*}$ , length $\begin{align*}b=5\end{align*}$ , place them end-to-end and they become the diameter of a semi-circle. Construct a perpendicular from the intersection of $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ to the circumference of the semi-circle, and the length of that perpendicular is the geometric mean. In this case, the geometric mean is 6.8 cm.
::使用上文描述的几何方法:长度 a=9, 长度 b=5, 将它们置于端到端, 成为半圆形的直径。构造从 a 和 b 交叉点到半圆形环绕的直径, 而该直径的长度是几何平均值。在这种情况下, 几何平均值为 6.8 cm 。

Example 2
::例2

Find the average rate of return on an investment that earns 6.04%, 6.89%, 7.22%, 6.92%, and 7.43% over successive years.
::连续几年赚取6.04%、6.89%、7.22%、6.92%和7.43%的投资平均回报率。

This problem is just like third third example in the text, just find the geometric mean of the interest rates:
::这个问题和案文中的第三位例子一样, 只需找到利率的几何平均值:

$\begin{aligned} \sqrt[5]{6.04 \times 6.89 \times 7.22 \times 6.92 \times 7.43} = \sqrt[5]{15, 448.569} = 6.88 % \end{aligned}$
$\begin{align*}\sqrt[5]{6.04 \times 6.89 \times 7.22 \times 6.92 \times 7.43}= \sqrt[5]{15, 448.569}=6.88 \%\end{align*}$

Example 3
::例3

Construct a visual representation of geometric mean of the numbers 23 and 38, using quadrilaterals.
::构造一个直观表示数字23和38的几何平均值,使用四边形。

This is just like the quadrilateral method described in the “Guidance” section: If you create a rectangle with side lengths equal to the numbers 23 and 38, then the side lengths of a square with the same area as the rectangle will be the geometric mean of the two numbers:
::这和“指导”一节中描述的四边法一样:如果您创建了侧长等于23和38的矩形,那么一个正方形的侧长与矩形的正方形的正方形相同,将是这两个数字的几何平均值:

Therefore, the geometric mean of 23 and 38 is 29.56 , just like the side length of the square.
::因此,23和38的几何平均值是29.56, 就像方形的侧长一样。

Example 4
::例4

Find the geometric and arithmetic mean of $\begin{align*}y\end{align*}$
::查找 y 的几何和算法平均值

The geometric mean is the 9 ^th root of the product of the values (since there are 9 values):
::几何平均值是数值产物的第9根根(因为有9个值):

$\begin{aligned} \sqrt[9]{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9} = \sqrt[9]{362, 880} = 4.147 \end{aligned}$
$\begin{align*}\sqrt[9]{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9}= \sqrt[9]{362, 880}=4.147\end{align*}$

The arithmetic root is the sum of the values divided by the count of the values:
::计算 root 是数值除以数数的数值的总和 :

$\begin{aligned} \frac{1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9}{9} = 5 \end{aligned}$
$\begin{align*}\frac{1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9}{9}=5\end{align*}$

Example 5
::例5

Find the mean proportional of the values: 12.34, 15.52, 16.82, 13.29, 13.91
::查找数值的平均值比例:12.34、15.52、16.82、13.29、13.91

There are five values here, so we need to find the 5 ^th root of the product:
::这里有五个值, 所以我们需要找到产品的第五根:

$\begin{aligned} \sqrt[5]{12.34 \times 14.52 \times 16.82 \times 13.29 \times 13.91} = \sqrt[5]{557, 134.28} = 14.1 \end{aligned}$
$\begin{align*}\sqrt[5]{12.34 \times 14.52 \times 16.82 \times 13.29 \times 13.91}= \sqrt[5]{557, 134.28}=14.1\end{align*}$

Review
::回顾

For questions 1-10, find the geometric mean of the numbers.
::对于问题1-10,请找到数字的几何平均值。

$\begin{align*}\{5, 8, 9, 7, 6, 8, 3, 4\} \end{align*}$

$\begin{align*}\{12, 16, 18, 13, 14, 16\} \end{align*}$

$\begin{align*}\{23, 24, 26, 28\} \end{align*}$

$\begin{align*}\{33, 37, 38, 36, 35, 35, 36, 34\} \end{align*}$

$\begin{align*}\{46, 49, 48, 41, 42, 43, 44\} \end{align*}$

$\begin{align*}\{51, 52, 53, 54, 55, 56, 57, 58, 59\}\end{align*}$

$\begin{align*}\{156.21, 245.25, 184.64, 222,32, 218.94, 134.88\}\end{align*}$

$\begin{align*}\{554, 564, 585, 525, 534, 500\} \end{align*}$

$\begin{align*}\{0.0021, 0.0034, 0.081, 0.009, 0.01, 0.258\} \end{align*}$

$\begin{align*}\left \{\frac{5}{8}, \frac{13}{21}, \frac{7}{9}, \frac{3}{5}, \frac{11}{23}\right \}\end{align*}$

Construct a semicircular representation of the mean proportional of the values 12 and 19.
::构造数值 12 和 19 的平均比例的半圆形表示数。

Construct a visual representation of the geometric mean of the numbers 5 and 8, using quadrilaterals.
::构造数字 5 和 8 的几何平均值的直观表示, 使用四边形。

Find the average rate of return on an investment that earns 5.02%, 4.11%, 4.18%, 3.72%, and 3.53% over successive years.
::连续几年赚取5.02%、4.11%、4.18%、3.72%和3.53%的投资的平均收益率。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。