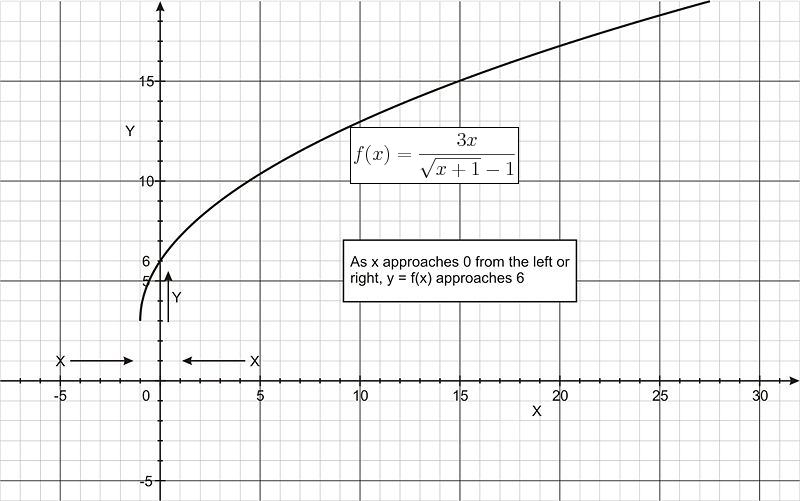Course: 8.1 限制的定义 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

限制的定义

Jim was watching his girlfriend run in a track meet. She was in the lead, and starting to pull away from the rest of the pack. Jim recognized a great photo opportunity, and snapped a great shot of Becca just as she rounded the corner and entered the homestretch.
::Jim看着他女朋友在赛道赛场上跑来跑去。她领先,并开始离开剩下的人群。Jim认出了一个伟大的拍照机会,在Becca转过角进入家庭时,她拍下了一张照片。

Later, they discussed the race over a victory ice cream, as they admired the photo. "You were really moving, Becca," Jim noted.
::后来,他们讨论了胜利冰淇淋的比赛,因为他们欣赏这张照片。吉姆指出,“你真的在动,贝卡”。

"I felt like I was flying!" Becca replied.
::"我觉得我在飞" Becca回答说

"I wonder how fast you were running at the exact time I took the photo?" Jim mused.
::"我不知道你跑多快正好是我拍照的时候?" Jim mused.

"That's easy!" Becca said. "Just take the distance of the race, and divide it by the time it took me to run. Here, hand me your phone, I'll run it through your calculator app, what was my time?"
::Becca说:“那很简单!” 贝卡说,“你只要距离赛跑,然后在我跑步的时候把它分开。在这里,把手机给我,我会通过你的计算器,我的时间是什么时候?”

"Hold on, Becca," Jim interjected. "I don't think that will work. You weren't running the same speed the entire race, so dividing your total distance by your total time isn't much more than an educated guess of your speed the instant I took the pic. Maybe we could use the official race recording, it will be time-stamped, and we could reference the track distance markers..."
::“等等,贝卡,”吉姆插嘴。“我不认为这样行得通。你跑的速度和整个赛跑的速度不同,所以你总距离除以你的全部时间, 只不过是我拍下那张照片的瞬间你的速度。也许我们可以使用正式的种族记录, 时间标记, 我们可以参考轨道距离标记...”

"Oh, come on Jim! There is no way we can know what my speed was at that instant !" Becca countered. " Any calculation we come up with is going to be no more than an approximation!"
::"哦,别这样,吉姆!我们不可能知道我当时的速度是多少!" Becca反调说,“我们的任何计算都会只是近似数字!”

Is Becca right?
::贝卡对吗?

Definition of a Limit
::限制的定义

The discovery of calculus was motivated by two fundamental geometric problems: finding the tangent line to a curve and finding the area of a planar region. In this section, we will show that these two problems are related to a deeper concept of calculus known as the limit of a function.
::微积分的发现是由两个基本的几何问题引起的:找到与曲线相切的线条和找到一个平板区域的区域。在本节中,我们将表明这两个问题与更深的微积分概念有关,这个概念被称为函数的极限。

The Two Fundamental Problems of Calculus that Lead to its Discovery:

The Tangent Line Problem: What is the equation of the tangent line to the graph f ( x ) at point P ( x ₀ , y ₀ )?
::切线问题: P(x0, y0) 点的图形 f(x) 的正切线的方程式是多少 ?

The Area Problem: What is the area between the graph f ( x ) and the x -axis in the interval [ a , b ]?
::区域问题:图f(x)与[a、b]间距的x轴之间的区域是什么?

The portion of calculus that deals with the tangent problem is called differential calculus and the portion that deals with the area problem is called integral calculus . In order to solve those two problems, we need to have a more precise understanding of what a tangent line is and what is meant by the area under a curve. Both of these issues require us to understand a deeper concept, the limit of a function.
::处理正切问题的微积分部分称为差异微分,处理地区问题的部分称为整体微分,为了解决这两个问题,我们需要更准确地了解正切线是什么,曲线下区域的含义是什么。这两个问题都要求我们理解更深的概念,即功能的极限。

Tangent Lines and Limits
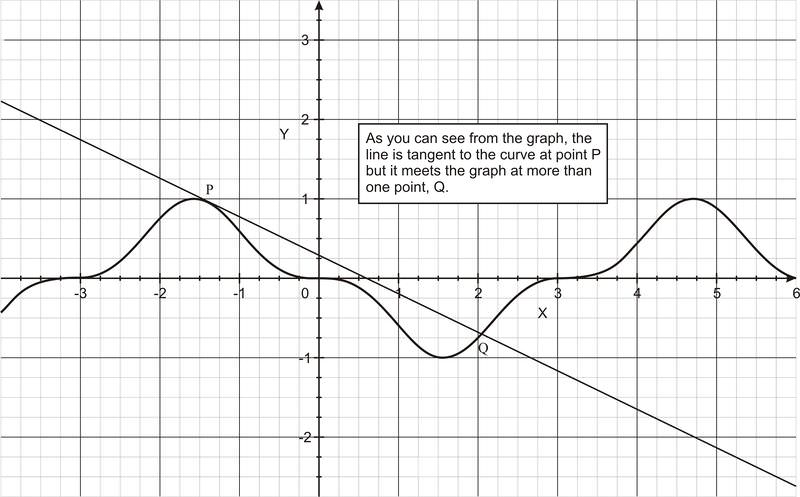
::定时线和界限

From your studies in geometry, you know that the tangent line is a line that intersects the circle at one point. However, this definition is not precise when we try to apply it to other kinds of curves. For example, as the figure below shows, one can draw a tangent line to a curve yet it cuts the curve at more than one point.
::从您的几何研究中, 您知道正切线是一个在某个点将圆交叉的线。但是, 当我们尝试将其应用于其他类型的曲线时, 这个定义并不精确。例如, 如下图所示, 人们可以将正切线绘制到曲线上, 但是它可以在不止一个点上切开曲线。

So we need to renew our concept of the tangent line and extend it to apply to curves other than circles. To do so, consider point P on the curve in the figure below. If point Q is any other point on the curve that is different from P , the line that passes through P and Q is called the secant line . Imagine if we move point Q along the curve toward point P , the secant line in this case will “rotate” toward a limiting position at point P . Eventually, the secant line will become a tangent line at point P , as the figure below shows. This is a new concept of the tangent line, where the general notion of a tangent line leads to the concept of limit. We will deal with the tangent line in more detail in lesson 8.3.
::因此,我们需要更新我们的正切线概念, 并将其扩展为适用于圆形以外的曲线。要这样做, 请考虑下图中曲线上的P点。如果Q点是曲线上与P不同的任何其他点, 穿过P和Q的线被称为松线。想象如果我们沿着向P点的曲线移动Q点, 这个案例中的松线将“ 旋转” 到P点的限制位置。最后, 如下图所示, 松线将变成P点的正切线。这是切线的新概念, 切线的一般概念将引向限制概念。我们将在8.3课中更详细地处理正切线。

Area as a Limit
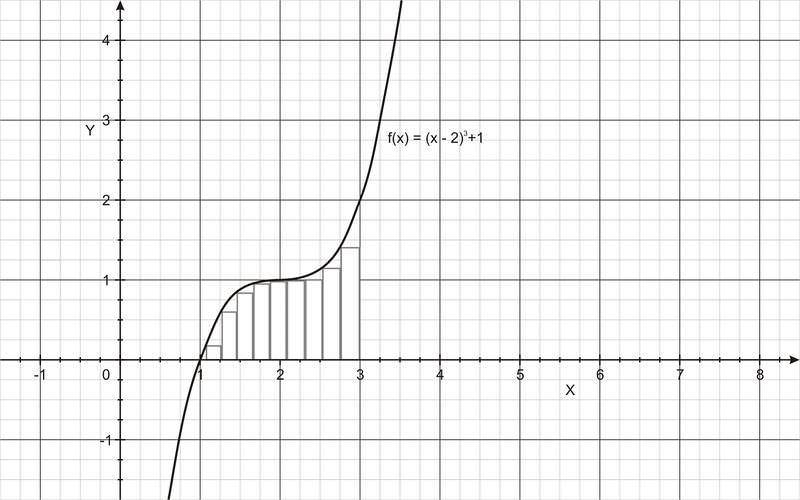
::以区域为限制

Suppose we are interested in finding the of a function on the interval [ a , b ]. For example, consider function f ( x ) = ( x - 2) ³ + 1 (the first figure below). Let’s say we want to approximate the area under the curve from x = 1 to x = 3. One way to do it is to inscribe rectangles of equal widths on the interval [1, 3] under the curve and then add the areas of these rectangles (the second figure below). Intuition tells us that if we repeat the process using more and more rectangles to fill the gaps under the curve, our approximation will approach the exact value of the area under the curve. So, the limiting value of this approximation is the exact value of the area under the curve. If we denote the width of each rectangle by ∆ x and the value of the area under the curve by A , then as ∆ x approaches zero (the widths of the rectangles get thinner and thinner, and thus less and less gaps), then the area A under the curve will reach an exact value.
::假设我们有兴趣在间距 [a, b] 上找到函数。例如, 考虑函数 f( x) = (x - 2) 3 + 1 (下面的第一个图)。假设我们想要将曲线下的区域从 x = 1 = x = = 3 = 3 。一种办法就是将相等宽度的矩形嵌入曲线下的间隔[ 1 , 3 , 然后添加这些矩形的区域( 下面第二个图案)。直观告诉我们, 如果我们重复该过程, 使用越来越多的矩形来填补曲线下的空白, 我们的近似将接近曲线下区域的确切值。因此, 这个近似值的极限值是曲线下区域的确切值。如果我们在曲线下将每个矩形的宽度用 x 和曲线下区域的宽度用 A 表示, 然后作为 + x 接近零 ( 矩形的宽度会变薄和稀薄, 从而缩小差距) , 那么曲线下的区域 A 将达到准确值。

What we have seen so far is that the concepts of tangent line and area rest on the notion of limit . In the next sections, we will explore those concepts in more details and show how the limit can help us calculate the rate of change of a given quantity. First, however, we introduce some useful notations.
::我们迄今为止所看到的是,正切线和地区的概念以限制的概念为基础。在接下来的章节中,我们将更详细地探讨这些概念,并表明限制如何帮助我们计算某一数量的变化速度。但是,首先,我们引入一些有用的符号。

Definition of a Limit (an informal view) The notation $\begin{aligned} lim_{x \to x_{0}} f (x) = L \end{aligned}$ means that as x approaches (or gets very close to) x ₀ , the limit of the function f ( x ) gets very close to the value L .

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about Jim and Becca's disagreement on whether it's possible to know her exact speed at a moment in the race.
::之前有人问过你吉姆和贝卡在比赛中能否知道她的确切速度

Technically, Becca is correct. However, using calculus to find the limit of her average speed at shorter and shorter intervals around the time the pic was taken could give Jim an answer that would be very, very close, as accurate as the race timer itself anyway.
::从技术上讲,贝卡是正确的。然而,利用微积分来找出她平均速度的极限,在照片拍摄时的间隔较短和短,这可以给吉姆一个非常接近的答案,与赛车计时器本身一样准确。

Example 2
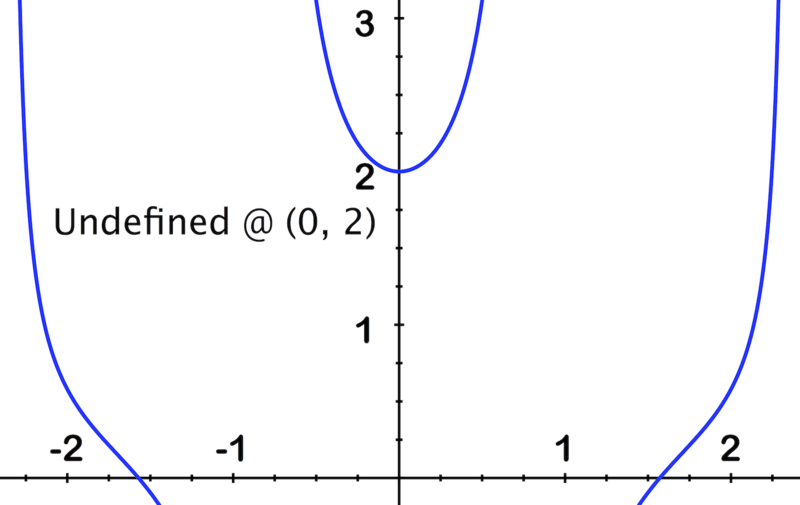
::例2

Make a conjecture about the value of the limit of $\begin{aligned} lim_{x \to 0} \frac{3 x}{\sqrt{x + 1} - 1} \end{aligned}$ .
::假设 limx+03xxx+1-1-1 限值的值。

Notice that the function $\begin{aligned} f (x) = \frac{3 x}{\sqrt{x + 1} - 1} \end{aligned}$ is not defined at x = 0. The table below shows samples of x -values approaching 0 from the left side and from the right side. In both cases, the values of f ( x ), calculated to at least 5 decimal places, get closer and closer to 6. Thus our conjecture is that $\begin{aligned} lim_{x \to 0} \frac{3 x}{\sqrt{x + 1} - 1} = 6 \end{aligned}$ .
::注意函数 f( x) = 3xx+1-1 - 1 未在 x = 0 上定义。下表显示左侧和右侧接近 0 的 x 值样本。在这两种情况下, F( x) 的值计算到小数点后至少 5 位, 接近和接近于 6 。因此,我们的推测是 limx= 03xx+1 - 1= 6 。

x	-0.01	-0.001	-0.0001	-0.00001	0	0.00001	0.0001	0.001	0.01
f ( x )	5.984962	5.9985	5.99985	5.999985	Undefined	6.000015	6.00015	6.0015	6.014963

Another way of seeing this is to graph f ( x ) (shown below). Notice that the x -values approach 0 from the left side and from the right side. In both cases, the values of f ( x ) appear to get closer and closer to 6.
::另一种观察方式是图f(x) (如下所示)。请注意,从左侧和右侧的 x 值接近0。在这两种情况下,f(x) 值似乎接近6。

Hence, again our conjecture is that $\begin{aligned} lim_{x \to 0} \frac{3 x}{\sqrt{x + 1} - 1} = 6 \end{aligned}$ .
::因此,我们的猜想再次是立方公尺03xxxx+1-1=6

Example 3
::例3

Make a conjecture about the value of the limit $\begin{aligned} lim_{x \to 0} \frac{s i n x}{x} \end{aligned}$ where x is in radians.
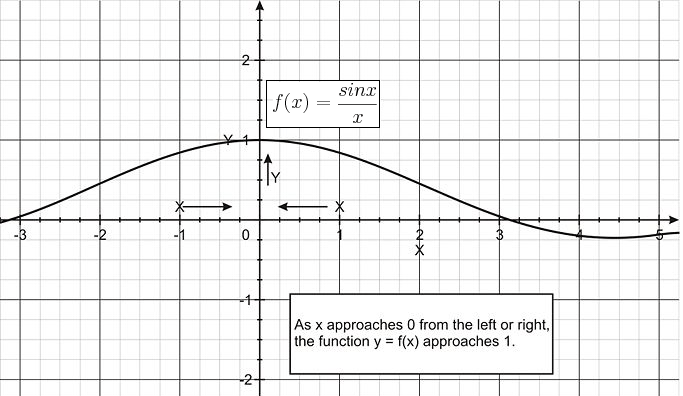
::假设x以弧度表示的极限 limx0sinxx 值。

The function here is not defined at x = 0. With the help of a computing utility, we can obtain the table below.
::这里的函数未在 x = 0 上定义。在计算工具的帮助下, 我们可以获取下表。

x	-0.2	-0.1	-0.01	0	0.01	0.1	0.2
f ( x )	0.993347	0.998334	0.999983	Undefined	0.999983	0.998334	0.993347

The data in the table suggest thats $\begin{aligned} lim_{x \to 0} \frac{s i n x}{x} = 1 \end{aligned}$ . The graph below supports this hypothesis.
::表中的数据表明,Limx0sinxx=1. 下图支持这一假设。

Example 4
::例4

Make a conjecture about the value of the limit $\begin{aligned} lim_{x \to 0} \frac{1 - c o s x}{x^{2}} \end{aligned}$ where x is in radians.
::假设x以弧度表示的极限 limx01-cosx22 值。

Enter the expression into your graphing calculator, or use this excellent free one here: .
::将表达式输入到您的图形计算器中,或者在此使用此优秀的自由表达式 : 。

You should get an image like the one below:
::你应该有一张像下面那张一样的图像:

It is clear from the graph that the limit is 1/2.
::从图中可以清楚地看出,限制是1/2。

Example 5
::例5

Use a grapher to make a conjecture about the value of the limit $\begin{aligned} lim_{x \to 0} \frac{t a n 2 x}{x} \end{aligned}$ .
::使用图形器对限值 limx+0tan2xx 进行推测。

Using a graphing tool:
::使用图形工具 :

The limit is 2.
::限值为2。

Example 6
::例6

Use limit notation to write "The limit of f ( x ) equals the cosine of x , as x approaches 2 from the right."
::使用限制符号写入“ f( x) 的限值等于 x 的余弦值, 因为 x 从右侧向上行 2 。 ”

$\begin{aligned} lim_{x \to 2^{+}} c o s x \end{aligned}$
::limx=%2+cosx

Review
::回顾

Write using limit notation:
::使用限制标记写入 :

Write the limit of $\begin{aligned} 4 x^{3} + 3 x^{2} - 4 x - 1 \end{aligned}$ as $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} a \end{aligned}$ from the left.
::写入 4x3+3x2-4x-1 的极限,作为从左侧向 a 方向的 x 。

Write the limit of $\begin{aligned} g (z) \end{aligned}$ as $\begin{aligned} z \end{aligned}$ approaches $\begin{aligned} a \end{aligned}$ from the left.
::写入 g(z) 的限制, 写为从左向左 z 接近 a 的 z 。

Write the limit of "> $\begin{aligned} g (y) \end{aligned}$ as $\begin{aligned} y \end{aligned}$ approaches $\begin{aligned} b \end{aligned}$ from the left.
::写上 g 的极限, 写为 y 向左接近 b 的 y 。

Write the limit of $\begin{aligned} h (z) \end{aligned}$ as $\begin{aligned} z \end{aligned}$ approaches $\begin{aligned} - 1 \end{aligned}$ from the right.
::将 h(z) 的限度写为 z 接近 -1 从右侧写入。

Write the limit of "> $\begin{aligned} h (y) \end{aligned}$ as $\begin{aligned} y \end{aligned}$ approaches $\begin{aligned} a \end{aligned}$ from the left.
::写入 h 的极限, 以向左 y 接近 a 。

Write the limit of $\begin{aligned} h (z) \end{aligned}$ as $\begin{aligned} z \end{aligned}$ approaches $\begin{aligned} a \end{aligned}$ .
::写入 h(z) 的限度, 以 z 接近 a 。

Solve using a calculator to estimate the limit:
::使用计算器估算极限值 :

$\begin{aligned} lim_{x \to 0} \frac{\sqrt{- 4 x + 2} - \sqrt{2}}{4 x} \end{aligned}$
::limx=0 - 4x+2 - 2 - 24x

$\begin{aligned} lim_{x \to - 1} \frac{- 8 x^{2} - 14 x - 6}{- 2 x - 2} \end{aligned}$
::1-8x2 - 14x - 6 - 6 - 2x-2

$\begin{aligned} lim_{x \to 0} \sec (\cos x) \end{aligned}$
::立方公尺( 立方公尺x)

$\begin{aligned} lim_{x \to \frac{- 16}{5}} \frac{\frac{- 2}{2 x + 2} - \frac{5}{11}}{- 10 x - 32} \end{aligned}$
::立方公尺 - 165 - 22x+2 - 511 - 10x-32

$\begin{aligned} lim_{x \to \frac{5}{2}} \frac{\sqrt{x + 5} - \sqrt{5}}{- 2 x + 5} \end{aligned}$
::limx=52x+5-5-5-2x+5

$\begin{aligned} lim_{x \to - 4} \frac{x^{2} + 6 x + 8}{x + 4} \end{aligned}$
::limx4x2+6x+8x+4

$\begin{aligned} lim_{x \to \frac{- 13}{2}} \frac{\frac{- 5}{2 x + 3} - \frac{1}{2}}{- 2 x - 13} \end{aligned}$
::132-52x+3-12-2x-13

$\begin{aligned} lim_{x \to 0} \cot (\sin x) \end{aligned}$
:sinx) (sinx)

$\begin{aligned} lim_{x \to 0} \frac{\sqrt{x + 3} - \sqrt{3}}{- 5 x} \end{aligned}$
::limx0x+3-3-3-5x

$\begin{aligned} lim_{x \to 0} \tan (\cos x) \end{aligned}$
:cosx) (cosx)

Write a formal definition for the following problems:
::为下列问题写一个正式定义:

%20%3D%20L"> $\begin{aligned} lim_{y \to 2} \tan (y) = L \end{aligned}$
:y)=L

$\begin{aligned} lim_{x \to 1} f (x) = N \end{aligned}$
::limx%1f(x)=N

$\begin{aligned} lim_{y \to - 1} - x^{3} + 2 x^{2} + 2 x + 4 = L \end{aligned}$
::Limy% 1 - x3+2x2+2x+4=L

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

限制的定义

Definition of a Limit ::限制的定义

Tangent Lines and Limits ::定时线和界限

Area as a Limit ::以区域为限制

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)