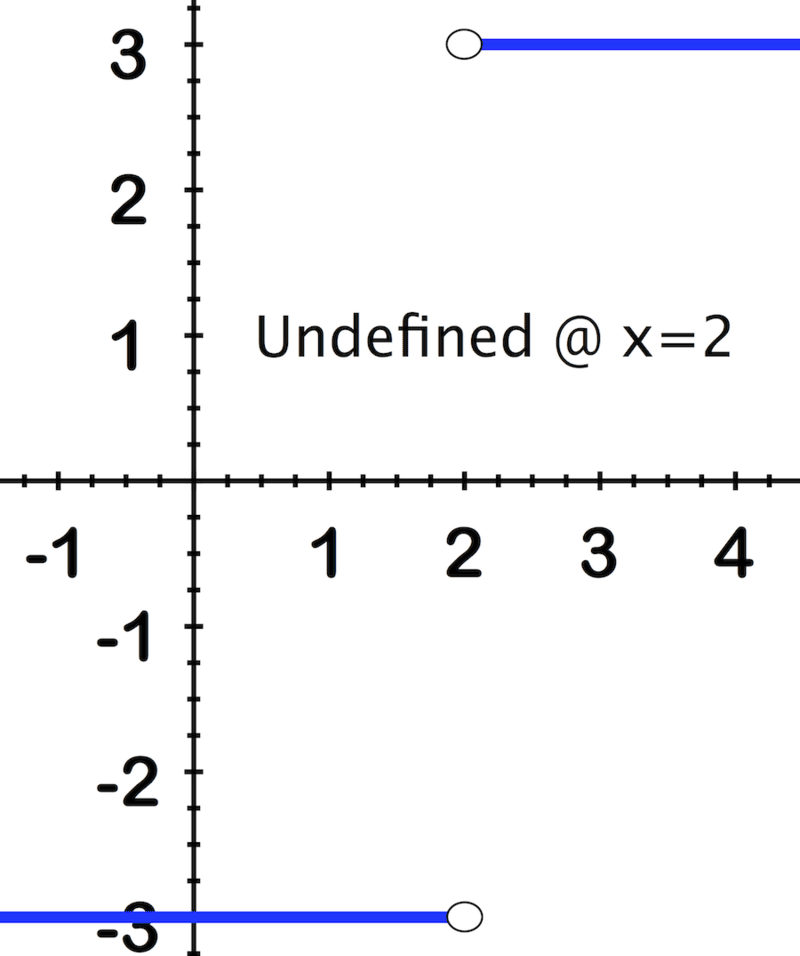8.2 单层限制

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 单设界限

  Collapse Expand

  单设界限

  播放段落

  Tuscany and Sophia were out hiking. As they followed the path up the side of a hill, they discovered that there had been a washout from the recent storm. The path had been obliterated for a space of about 15 feet in front of them, thereafter it continued on up the mountain from about 10 feet higher.
  ::托斯卡尼和索菲亚正在徒步旅行。 当他们沿着山坡上的路行走时,他们发现最近暴风雨已经冲洗过。 这条路在他们前面大约15英尺的地方被抹去,随后从大约10英尺高处一直沿着山上走下去。

  播放段落

  How could this situation be explained with ?
  ::如何解释这种情况?

  播放段落

  One-Sided Limits
  ::单设界限

  播放段落

  Unlike the functions from prior lessons where the limit was the same from both directions, the functions we explore in this lesson may have a different limit for each "side." To evaluate these functions, we deal with each "side" separately, first evaluating what happens as the limit is approached from either the positive direction (the values of x are bigger than at the limit) or the negative direction (the values of x are smaller than at the limit) and then evaluating the other direction afterward as if it were effectively a separate function.
  ::与以往教训中的功能不同, 两者的限制相同, 我们在此教训中探讨的功能对每个“ 侧” 可能有不同的限制 。 为了评估这些功能, 我们分别处理每个“ 侧” , 首先从正方向( x 的值大于极限) 或负方向( x 的值小于极限) 来评估所接近的限制, 然后将另一个方向作为独立功能来评估。

  播放段落

  Sometimes the same value is approached from either "side" of the limit value, and some functions have different limits on the two sides of x = x ₀ .
  ::有时从极限值的“侧面”取出相同的值,有些函数在 x = x0 的两侧有不同的限制。

  播放段落

  When the value of f ( x ) does not get closer and closer to some single value L as $\begin{align*}x \rightarrow x_0\end{align*}$ we say that the limit of the function as x approaches x ₀ does not exist . We may separately state the limits for each "side" of x ₀ , but the complete function will only have a specified limit if it is the same for both sides.
  ::当 f( x) 的值没有接近或接近某些单一值L 作为 xx0 时, 我们就会说, x 接近x0 的函数限制不存在。 我们可以分别说明 x0 的每个“ 侧边” 的值限制, 但完整函数只有两边相同时才有特定限制 。

  播放段落

  For example, the two-sided limit of the complete function $\begin{align*}lim_{x \rightarrow 0} \frac{ |x|}{x}\end{align*}$ does not exist because the values of f ( x ) do not approach a single number as x approaches 0. We can state the one-sided limits for each side, since the values approach -1 from the left and 1 from the right.
  ::例如,完整函数 limx0xx 的双向限制并不存在,因为 f(x) 的值没有像 x 接近 0 一样接近一个数字。 我们可以为每侧说明单向限制, 因为值方法 - 1 从左侧, 1 从右侧。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked a question about how to represent a situation as a one-sided limit.
  ::早些时候,有人问你一个问题,即如何将局势作为片面的限制来代表。

  播放段落

  Tuscany and Sophia's path could be examined as a discontinuous function of elevation based on distance traveled along the path. For instance, if Tuscany and Sophia had traveled for 500 yards along the path before encountering the washout, then the limit of the function from the "trailhead side" would be the elevation at the edge they encountered. The function would then be undefined for the next 5 yards or so (since the path does not exist), and would pick up at 506 yards, where the elevation would be 10ft higher. If Sayber were coming down the path toward Tuscany and Sophia, from his point of view the "limit" of the elevation would be 10ft greater, and would be the lowest elevation that "his side" of the function could attain.
  ::托斯卡尼和索菲亚的路径可以作为一个不连续的高度函数来检查, 以沿路行走的距离为基础。 例如, 如果托斯卡尼和索菲亚在冲洗前沿路行了500码, 那么“ 铁头边” 的功能的极限就是他们遇到的边缘的高度。 然后, 该功能将被下5码左右的高度( 因为路径不存在 ) , 并且会回到506码, 高度会高10英尺。 如果赛伯在通往托斯卡尼和索菲亚的道路上走下去, 从他的角度看, 高度的“ 界限” 将会更大10英尺, 并且是“ 他一边” 函数可以达到的最低高度 。

  播放段落

  Example 2
  ::例2

  播放段落

  Identify the limit of the function: $\begin{align*}f(x) = \frac{|x|} {x} = \begin{cases} 1, x > 0\\ -1, x < 0\\ \end{cases} \end{align*}$
  ::指定函数的极限 : f(x) xxxx1x>0- 1,x <0

  播放段落

  which is shown in the graph below:
  ::如下图所示:

  

  播放段落

  As x approaches 0 from the right, f ( x ) approaches 1. On the other hand, as x approaches 0 from the left, the function f ( x ) approaches -1. Since the limit is not the same from both sides, the limit of the function does not exist. However we can say that:
  ::1. 另一方面,当x向左接近0时,函数f(x)向左走0时,函数f(x)向右走1。由于两边的限制不同,函数的极限并不存在。但我们可以说:

  播放段落

  $\begin{align*}\lim_{x \rightarrow 0^+} \frac{|x|} {x} = 1\end{align*}$
  ::立方公尺xxx=1

  播放段落

  $\begin{align*}\lim_{x \rightarrow 0^-} \frac{|x|} {x} = -1\end{align*}$
  ::立方公尺#0###################################################################################################################################################################################1####################################1###################################################################################################################################1##########################################################################################################################################################

  播放段落

  Where the superscript “+” indicates a limit from the right and the superscript “-” indicates a limit from the left.
  ::当上标“+”表示右侧的限值时,上标“-”表示左侧的限值。

  播放段落

  Example 3
  ::例3

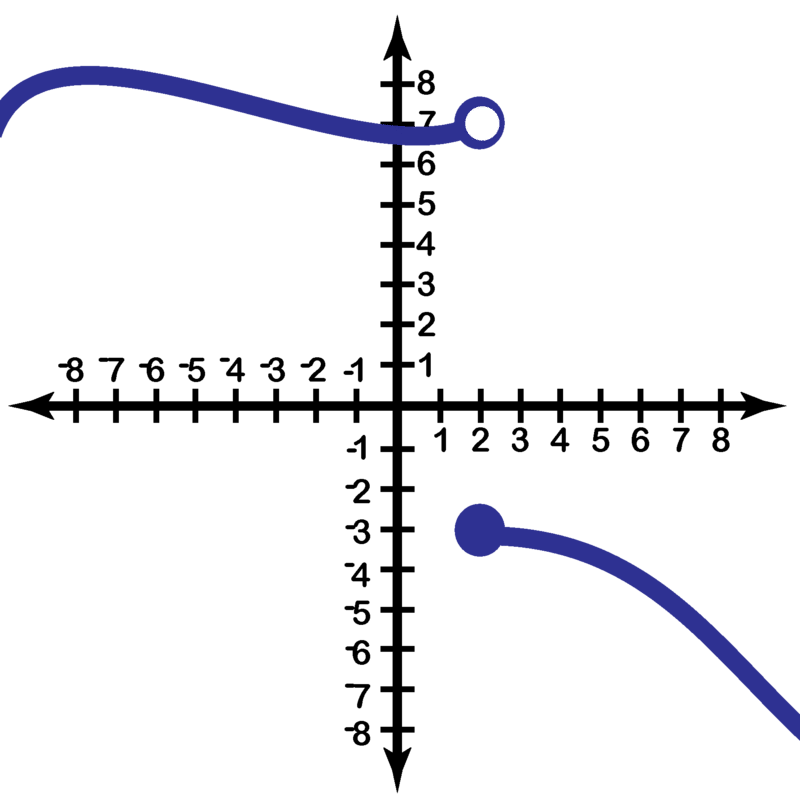
  播放段落

  Consider the function f graphed  below:
  ::考虑以下图表显示的函数 f :

  

  播放段落

  Find:
  ::查找 :

  播放段落
  1. $\begin{align*} \lim_{x \rightarrow 2^-}f(x)\end{align*}$
     ::limx%2 - f(x)

  播放段落

  From graph, we can see that, $\begin{align*}\lim_{x \rightarrow 2^-}f(x) = -2\end{align*}$ .
  ::从图表中,我们可以看到,2-f(x)2。

  播放段落
  2. $\begin{align*} \lim_{x \rightarrow 2^+}f(x)\end{align*}$
     ::limx%2+f(x)

  播放段落

  We can also see from the graph that $\begin{align*}\lim_{x \rightarrow 2^+}f(x) = 4\end{align*}$ .
  ::我们也可以从图中看到2+f(x)=4。

  播放段落
  3. $\begin{align*}\lim_{x \rightarrow 2}f(x)\end{align*}$
     ::limx%2f(x)

  播放段落

  Since the limits from the right and the left are not equal (they do not approach a single value L ), the limit does not exist. That is, $\begin{align*} \lim_{x \rightarrow 2}f(x) \end{align*}$ does not exist.
  ::由于右和左的限值不相等(它们不接近单一值L),因此这一限值不存在。也就是说, limx%2f(x) 不存在 。

  播放段落
  4. $\begin{align*}f(2)\end{align*}$
     ::f(2) f(2)

  播放段落

  $\begin{align*}f(2)=1\end{align*}$
  ::f(2)=1

  播放段落

  Example 4
  ::例4

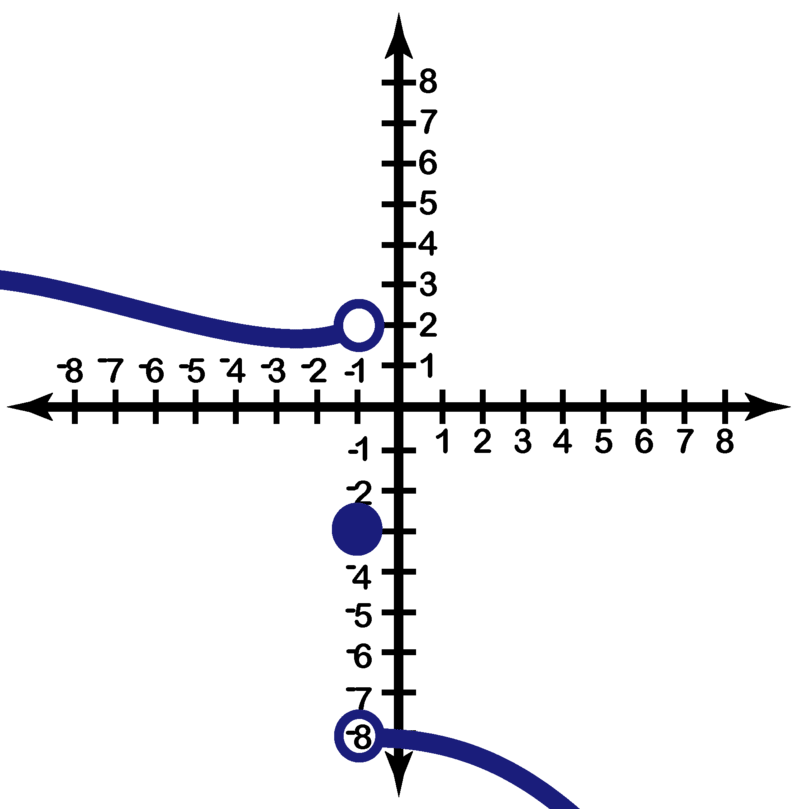
  播放段落

  Consider $\begin{align*}g(x) = \frac{|x - 2|}{x - 2}|3|\end{align*}$ in the image below:
  ::在下面的图像中考虑 g( x) x- 2x- 2x- 233:

  

  播放段落

  Find:
  ::查找 :

  播放段落
  1. $\begin{align*} \lim_{x \rightarrow 2^-}f(x)\end{align*}$
     ::limx%2 - f(x)

  播放段落

  From graph, we can see that, $\begin{align*}\lim_{x \rightarrow 2^-}f(x) = -3\end{align*}$ .
  ::从图表中,我们可以看到,2-f(x)+3。

  播放段落
  2. $\begin{align*} \lim_{x \rightarrow 2^+}f(x)\end{align*}$
     ::limx%2+f(x)

  播放段落

  We can also see from the graph that $\begin{align*}\lim_{x \rightarrow 2^+}f(x) = 3\end{align*}$ .
  ::我们也可以从图中看到2+f(x)=3。

  播放段落
  3. $\begin{align*}\lim_{x \rightarrow 2}f(x)\end{align*}$
     ::limx%2f(x)

  播放段落

  Since the limits from the right and the left are not equal (they do not approach a single value L ), the limit does not exist. That is, $\begin{align*} \lim_{x \rightarrow 2}f(x) \end{align*}$ does not exist.
  ::由于右和左的限值不相等(它们不接近单一值L),因此这一限值不存在。也就是说, limx%2f(x) 不存在 。

  播放段落
  4. $\begin{align*}f(2)\end{align*}$
     ::f(2) f(2)

  播放段落

    $\begin{align*}f(2) = \not0\end{align*}$ undefined
  ::f(2)% 0 未定义

  播放段落

  Example 5
  ::例5

  播放段落

  Identify the limit based on the equation:
  ::根据等式确定界限:

  播放段落

  $\begin{align*}g(x)= \begin{cases} 7; x = - 5\\ 2; x \not= -5\\ \end{cases} \end{align*}$
  ::g( x) @ @% 7; x @ @ @ 52; x @ 5

  播放段落

  The cases specify that if $\begin{align*}x = -5\end{align*}$ then $\begin{align*}g(x) =7\end{align*}$ and if $\begin{align*}x\end{align*}$ is anything else, then $\begin{align*}g(x) = 2\end{align*}$
  ::实例指定,如果 x5 然后 g( x)=7, 如果 x 是其它东西, 那么 g( x)=2

  播放段落

  $\begin{align*}\therefore\end{align*}$ the limit as x approaches -5 from either direction is 2.
  ::++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++xxxxxxxx 5-5-5+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

  播放段落

  Example 6
  ::例6

  播放段落

  Identify the limit based on the equation, use a graphing tool:  $\begin{align*}\lim_{x\to3^+}\frac{x^2 - 5x + 6}{x - 3}\end{align*}$ .
  ::确定基于方程的限值,使用图形工具: limx%3+x2- 5x+6x- 3。

  播放段落

  Factor the numerator: $\begin{align*}(x - 2)(x - 3)\end{align*}$
  ::乘以乘数数x-2)(x-3)

  播放段落

  Now that you now have $\begin{align*}(x - 3)\end{align*}$ in the numerator and in the denominator
  ::现在,你们在分子和分母中有(x-3),

  播放段落

  Substitute 3 in for x in $\begin{align*}x - 2\end{align*}$ since 3 is the number we want to evaluate
  ::x-2 x 中的 x 3 的替代 3 英寸, 因为 3 是我们要评估的数量

  $\begin{align*}3 - 2 = 1\end{align*}$

  播放段落

  $\begin{align*}\therefore \lim_{x\to3^+}\frac{x^2 - 5x + 6}{x - 3} = 1\end{align*}$
  ::*%x%3+x2-5x+6x-3=1

  播放段落

  Review
  ::回顾

  播放段落

  Identify the limit, based on each graph.
  ::以每个图表为基础,标明界限。

  播放段落
  1. $\begin{align*}\lim_{x\to-3^-}\end{align*}$
     ::3 - 3 - 3 -
  播放段落
  2. $\begin{align*}\lim_{x\to2^+}\end{align*}$
     ::limx%2+
  播放段落
  3. $\begin{align*}\lim_{x\to-1^+}\end{align*}$ and $\begin{align*}\lim_{x\to-1^-}\end{align*}$
     ::limx1+ 和limx1-
  播放段落
  4. $\begin{align*}\lim_{x\to-1}\end{align*}$
     ::立方公尺1
  播放段落
  5. $\begin{align*}\lim_{x\to-2^-}\end{align*}$ and $\begin{align*}\lim_{x\to5^+}\end{align*}$
     ::limx%2 - 和limx=5+

  播放段落

  Identify the limit based on the equation:
  ::根据等式确定界限:

  播放段落
  6. $\begin{align*}\lim_{x\to2^+}\frac{-x^2 - 2x + 8}{x - 2}= \end{align*}$
     ::立方公尺xx2x2 - 2x+8x-2=
  播放段落
  7. $\begin{align*}g(x)= \begin{cases} 4; x = - 3\\ 1; x \not= -3\\ \end{cases}\end{align*}$
     ::g( x) 4; x 31; x 3
  播放段落
  8. $\begin{align*}\lim_{x\to0^+}\frac{-x^2 + 4x}{x}= \end{align*}$
     ::立方公尺xxx2+4xx=
  播放段落
  9. $\begin{align*}g(x)= \begin{cases} -5; x \not= -1\\ -1; x = -1\\ \end{cases} \end{align*}$
     ::g( x)\\% 5; x\\% 1 - 1; x\% 1
  播放段落
  10. $\begin{align*}\lim_{x\to1^+}\frac{4x^2 - x - 3}{x - 1}= \end{align*}$
      ::limx%1+4x2-x-3x-1=
  播放段落
  11. $\begin{align*}f(x)= \begin{cases} 4 ; x \geq 3\\ x + 1; x < 3\\ \end{cases} \end{align*}$
      ::f( x)\\\\\\ 4; x=3x+1; x < 3
  播放段落
  12. $\begin{align*}\lim_{x\to0^+}\frac{x^2 - 4x}{x}= \end{align*}$
      ::limx=0+x2-4xx=
  播放段落
  13. $\begin{align*}h(x)= \begin{cases} 4x + 4 ; x \not= 2\\ 1 ; x = 2\\ \end{cases} \end{align*}$
      ::h(x) 4x+4;x21;x=2
  播放段落
  14. $\begin{align*}\lim_{x\to2^-}\frac{4x^2 - 7x - 2}{x - 2}= \end{align*}$
      ::2 - 4x2 - 7x - 2x-2=
  播放段落
  15. $\begin{align*}g(x)= \begin{cases} x - 5 ; x = -2\\ 4x + 1 ; x \not= -2\\ \end{cases} \end{align*}$
      ::g( x) x- 5; x24x+1; x2
  播放段落
  16. $\begin{align*}g(x)= \begin{cases} -3x ; x\not= 3\\ -9 ; x = 3\\ \end{cases} \end{align*}$
      ::g (x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x=3\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
  播放段落
  17. $\begin{align*}\lim_{x \to -5^-}\frac{-3x^2 - 13x + 10}{x + 5}= \end{align*}$
      ::立方公尺xx5x3x2-13x+10x+5=
  播放段落
  18. $\begin{align*}f(x)= \begin{cases} x ; x = 2\\ 3x - 3 ; x \not= 2\\ \end{cases} \end{align*}$
      :xx) x;x=23x-3;x2

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。