Course: 8.6 单层限制的适用

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

A. 单层限制的适用

Early in this section, we practiced finding . In this lesson we will be using that skill and applying it with the rule of limits that says a function must have the same limit from each side in order to have a single limit.
::在本节的早期,我们练习了发现。在这个教训中,我们将使用这种技能,并运用限制规则,规定一个函数必须具有来自每一方的相同限制,才能有一个单一的限制。

That process allows us to first determine if a function has a limit, and then find the limit if it exists, even if we cannot actually determine the limit directly.
::这一过程使我们能够首先确定一个函数是否有限制,然后找到存在的限制,即使我们无法直接实际确定限制。

Applications of One-Sided Limits
::A. 单层限制的适用

When we wish to find the limit of a function f ( x ) as it approaches a point a and we cannot evaluate f ( x ) at a because it is undefined at that point, we can compute the function's one-sided limits in order to find the desired limit. If its one-sided limits are the same, then the desired limit exists and is the value of the one-sided limits. If its one-sided limits are not the same, then the desired limit does not exist . This technique is used in the examples below.
::当我们想在函数f(x)接近一个点时找到函数f(x)的极限,而由于 f(x)当时没有定义,因此无法对f(x)进行评价时,我们可以计算函数的片面限制,以便找到理想的极限。如果其单面限制相同,那么理想的极限就存在,是单面限制的价值。如果其单面限制不同,则没有理想的极限。下面的例子中就使用了这一方法。

Conditions for a Limit to Exist ( The relationship between one-sided and two-sided limits )

In order for the limit L of a function to exist, both of the one-sided limits must exist at x ₀ and must have the same value. Mathematically,

\begin{aligned} lim_{x \to x_{0}} f (x) = L \end{aligned}

$\begin{align*}\lim_{x \rightarrow x_0} f(x) = L\end{align*}$ if and only if

\begin{aligned} lim_{x \to x_{0}^{-}} f (x) = L \end{aligned}

$\begin{align*}\lim_{x \rightarrow x_0^-} f(x) = L\end{align*}$ and

\begin{aligned} lim_{x \to x_{0}^{+}} f (x) = L \end{aligned}

$\begin{align*}\lim_{x \rightarrow x_0^+} f(x) = L\end{align*}$ .

The One-Sided Limit

If f ( x ) approaches L as x approaches x ₀ from the left and from the right, then we write

\begin{aligned} lim_{x \to x_{0}^{+}} f (x) = L \end{aligned}

$\begin{align*}\lim_{x \rightarrow x_0^+} f(x) = L\end{align*}$

\begin{aligned} lim_{x \to x_{0}^{-}} f (x) = L \end{aligned}

$\begin{align*}\lim_{x \rightarrow x_0^-} f(x) = L\end{align*}$

which reads: “the limit of f ( x ) as x approaches

\begin{aligned} x_{0}^{+} \end{aligned}

$\begin{align*}x_0^+\end{align*}$ (or

\begin{aligned} x_{0}^{-} \end{aligned}

$\begin{align*}x_0^-\end{align*}$ ) from the right (or left) is L .

Examples
::实例

Example 1
::例1

Find the limit f ( x ) as x approaches 1. That is, find $\begin{align*}\lim_{x \rightarrow 1} f(x)\end{align*}$ if
::查找限制 f(x) 的 f(x) f 值为x 接近点。也就是说, 找到 limx%1f(x) , 如果

	$\begin{align}f(x) = \begin{cases}3 - x, & x < 1 \\ 3x - x^2, & x > 1 \end{cases}\end{align}$

Remember that we are not concerned about finding the value of f ( x ) at x but rather near x . So, for x < 1 (limit from the left),
::记住我们并不关心在 x 找到 f(x) 值,而是在 nearx 值。所以, x < 1 (左侧限制),

	$\begin{align}\lim_{x \rightarrow 1^{-}} f(x) = \lim_{x \rightarrow 1^{-}} (3 - x) = (3 - 1) = 2\end{align}$

and for x > 1 (limit from the right),
::和 x > 1 (对权利的限制),

	$\begin{align}\lim_{x \rightarrow 1^+} f(x) = \lim_{x \rightarrow 1^+} (3x - x^2) = 2\end{align}$

Now since the limit exists and is the same on both sides, it follows that
::现在既然双方的限额都存在,而且双方的限额相同,那么,

	$\begin{align}\lim_{x \rightarrow 1} f(x) = 2\end{align}$

Example 2
::例2

Find $\begin{align*}\lim_{x \rightarrow 2} \frac{3} {x - 2}\end{align*}$ .
::查找 limx23x-2 。

From the figure below we see that $\begin{align*}f(x)=\frac{3} {x - 2}\end{align*}$ decreases without bound as x approaches 2 from the left and $\begin{align*}f(x)=\frac{3} {x - 2}\end{align*}$ increases without bound as x approaches 2 from the right.
::从下图中可以看出,F(x)=3x-2的减少与x方针2从左边和f(x)=3x-2从右边不加约束地增加,而x方针2从右边不受约束。

This means that $\begin{align*}\lim_{x \rightarrow 2^-} \frac{3} {x - 2} = -\infty\end{align*}$ and $\begin{align*}\lim_{x \rightarrow 2^+} \frac{3} {x - 2} = +\infty\end{align*}$ . Since f ( x ) is unbounded (infinite) in either directions, the limit does not exist.
::这意味着 limx%2 - 3x-2 和 limx%2+3x-2。由于 f(x) 在两个方向上都没有约束( 无限) , 限制并不存在。

Example 3
::例3

For an object in free fall, such as a stone falling off a cliff, the distance y ( t ) (in meters) that the object falls in t seconds is given by the kinematic equation y ( t ) = 4.9 t ² . The object’s velocity after 2 seconds is given by $\begin{align*}v(t) = \lim_{t \rightarrow 2} \frac{y(t) - y(2)} {t - 2}\end{align*}$ .
::对于自由坠落的物体,例如从悬崖上掉下来的石头,物体在t秒内坠落的距离 y(t) y(t) = 4.9 t2. 该物体在2秒后的速度由 v(t) =limt2y(t)-y(2)t-2 给出。

What is the velocity of the object after 2 seconds?
::2秒后天体的速度是多少?

The limit is 19.6 secs. The function can be plotted on a graphing tool, and at 1.999, the graph looks like this:
::限制为19.6秒。函数可以在图形工具上绘制,在1.999时,图形看起来是这样的:

You can see the result of smaller values of t , by adjusting the t slider on the active graph here: .
::您可以通过调整活动图中的 t 滑动器来看到 t 较小值的结果 : 。

Example 4
::例4

Find $\begin{align*} \lim_{x \rightarrow 0^+} (\pi)\end{align*}$ .
::查找 limx=%0+(__) 。

If a and k are real numbers, then $\begin{align*}\lim_{x\rightarrow a}k = k\end{align*}$ .
::Ifaandkare 真实数字,然后limxQQAK=K。

$\begin{align*}\therefore \lim_{x \rightarrow 0^+} (\pi) = \pi\end{align*}$
::=============================================================================================================================== ================================================================================================

Example 5
::例5

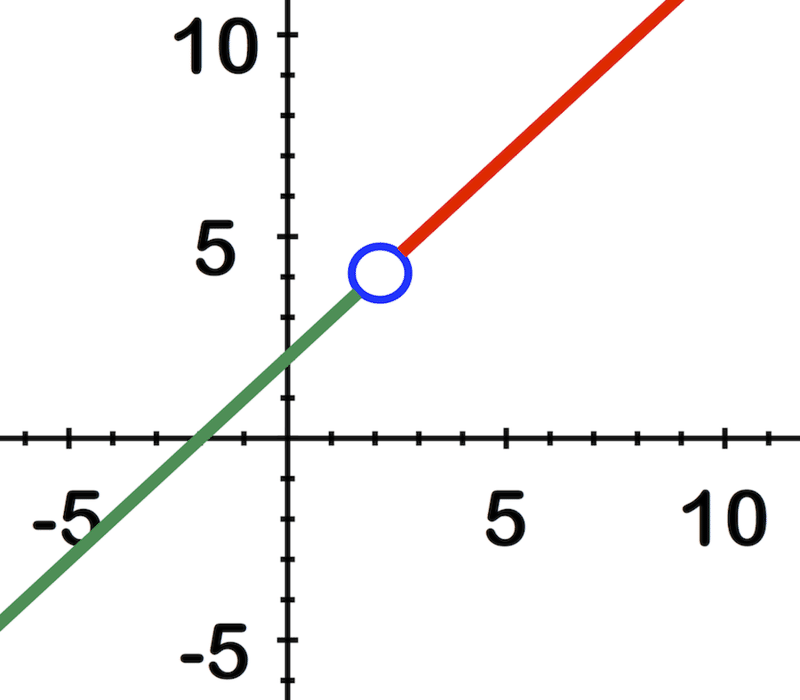
Find $\begin{align*} \lim_{x \rightarrow 2} \frac{x^2 - 4} {x - 2}\end{align*}$ .
::查找 limx% 2x2 - 4x- 2 。

The limit is 4, as shown in the image below. The red line approaches from values above x = 2, and the green line from below. The line is undefined where they meet. This can be examined in greater detail at: .
::限制为 4 , 如下图所示。从 x = 2 上方的值向红线方向, 从下方的绿线方向向下方的值向红线方向。这条线在它们相遇的地方没有定义。可以在下列地点进行更详细的检查: 。

Example 6
::例6

Find $\begin{align*} \lim_{x \rightarrow 6} \frac{x - 6} {x^2 - 36}\end{align*}$ .
::查找 limx_6x_6x2_36。

The limit is $\begin{align*}\frac{1}{12}\end{align*}$ .
::限额为112。

Interact with the graph here:
::与此图交互 :

or make a table:
::或设置表格:

x 5 7 5.5 6.5	f(x) 1/11 1/13 2/23 2/25

Example 7
::例7

Find $\begin{align*} \lim_{x \rightarrow 5} \sqrt{x^3 - 2x - 1}\end{align*}$ .
::查找 limx=5x3- 2x- 1 。

The limit is $\begin{align*}\sqrt{114}\end{align*}$ or $\begin{align*}\approx 10.667\end{align*}$ .
::限值为114或10.667。

Interact with the graph here: .
::与此图的交互作用 : 。

Review
::回顾

Based on the graph, determine if a limit exists:
::根据图表,确定是否存在限制:

Determine if a limit exists:
::确定是否存在限制 :

$\begin{align*}\lim_{x \to 0} \frac{4x^2}{x}\end{align*}$
::limx04x2x

$\begin{align*} g(x)= \begin{cases} -2 ; x = - 2\\ -3x + 3 ; x \not= -2\\ \end{cases} \end{align*}$
::g( x) 2; x2 - 3x+3; x2

$\begin{align*}\lim_{x \to 3} \frac{-x^2 + 9}{x - 3}\end{align*}$
::limx=3 - x2+9x-3

$\begin{align*} g(x)= \begin{cases} 3 ; x \geq -1\\ x + 4 ; x < -1\\ \end{cases} \end{align*}$
::g (x)\\\\\% 3;x\\\\\\1x+4;x\\\1)

$\begin{align*}\lim_{x \to 3} \frac{4x^2 - 15x + 9}{x - 3}\end{align*}$
::立方公尺

$\begin{align*} h(x)= \begin{cases} -2; x \geq -1\\ -5x + 2 ; x < -1\\ \end{cases} \end{align*}$
::h( x) 2; x1 - 5x+2; x1

$\begin{align*}\lim_{x \to {-1}} \frac{4x^2 - 4}{x + 1}\end{align*}$
::limx14x2 - 4x+1

$\begin{align*} g(x)= \begin{cases} -3 ; x > 0\\ x - 3 ; x \leq 0\\ \end{cases} \end{align*}$
::g( x)\%% 3; x> 0x- 3; x% 0

$\begin{align*}\lim_{x \to -4} \frac{x^2 + 5x + 4}{x + 4}\end{align*}$
::limx4x2+5x+4x+4

$\begin{align*} g(x)= \begin{cases} -3x - 4 ; x = 3\\ -2x - 1 ; x \not= 3\\ \end{cases} \end{align*}$
::g (x) 3x- 4;x= 3- 2x- 1;x=3

$\begin{align*}\lim_{x \to -4} \frac{-3x^2 - 15x - 12}{x + 4}\end{align*}$
::limx*%4 - 3x2 - 15x - 12x+4

$\begin{align*} g(x)= \begin{cases} 4 ; x \leq -3\\ 3 ; x > -3\\ \end{cases} \end{align*}$
::g( x) 4; x% 33; x3

$\begin{align*}\lim_{x \to 2} \frac{2x^2 - 4x}{x - 2}\end{align*}$
::立方厘米x22x2-4xx-2

$\begin{align*} f(x)= \begin{cases} -3 ; x = -1\\ -2 ; x \not= -1\\ \end{cases} \end{align*}$
::f( x)\\\\\ 3; x\\\\ 2; x\\ 1

$\begin{align*} \lim_{x \rightarrow 3^+} \frac{3} {x - 3}\end{align*}$ .
::立方厘米3+3x-3。

Show that $\begin{align*}\lim_{x \rightarrow 0^+} \left (\frac{1} {x} - \frac{1} {x^2}\right ) = -\infty\end{align*}$ .
::显示 limx=0+(1x- 1x2)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

A. 单层限制的适用

Applications of One-Sided Limits ::A. 单层限制的适用

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)