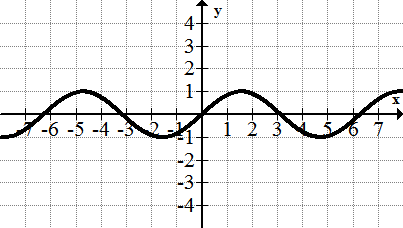Course: 1.4 域和范围 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

域和范围

Analyze means to examine methodically and in detail. One way to analyze functions is by looking at possible inputs (domain) and possible outputs (range). Which of the basic functions have limited domains and why?
::分析分析功能的方法之一是研究可能的投入(领域)和可能的产出(范围)。哪些基本功能范围有限,为什么?

Domain and Range
::域和范围

Notation
::标注

Domain and range are described in interval notation. " data-term="Parentheses" role="term" tabindex="0"> Parentheses , , mean non-inclusive. Brackets , [ ], mean inclusive. The following descriptions of numbers have been converted to interval notation.
::域和范围以间距符号表示。括号 , 平均值不包含。括号 , 平均值含括号 , 平均值含括号。以下数字描述已被转换为间距符号。

All numbers.
::所有数字。

$\begin{aligned} (- \infty, \infty) \end{aligned}$ Note: Parentheses are always used with infinity.
::注:括号总是无穷无尽地使用。

All negative numbers not including 0.
::所有负数不包括0。

$\begin{aligned} (- \infty, 0) \end{aligned}$

All positive numbers including 0.
::所有正数,包括0。

$\begin{aligned} [0, \infty) \end{aligned}$

Every number between 1 and 4 including 1 and 4.
::1到4之间每一数字,包括1和4。

[1, 4]

Every number between 5 and 6 not including 5 or 6.
::5到6之间的每一数字,不包括5或6。

(5, 6)

The numbers 1 through 2, including 1 but not including 2, and the numbers 10 through 25, including both 10 and 25
::1至2号,包括1号至2号,不包括2号,10号至25号,包括10号和25号

$\begin{aligned} [1, 2) \cup [10, 25] \end{aligned}$

Note: The $\begin{aligned} \cup \end{aligned}$ symbol means Union and refers to the fact that if some number $\begin{aligned} x \end{aligned}$ is in this union, then it is either in the first group or it is in the second group. This symbol is associated with the OR statement. While it is true that the Union symbol seems to bring one group and another group together, the symbol for AND is $\begin{aligned} \cap \end{aligned}$ which means intersection . Intersection is different from union because intersection means all numbers that are in both the first group and second group at the same time.
::注: {{{{{{}} 符号是指联盟, 并指如果某个数字 x 属于该联盟, 那么它要么属于第一个组, 要么属于第二个组。}此符号与 OR 声明有关。虽然该符号似乎将一个组和另一个组集合在一起, 但该符号是和 {} 的符号, 表示交叉。 {}} 互交与联盟是不同的, 因为交叉是指同时同时同时同时属于第一个组和第二个组的所有数字。 {}}}}

Domain and Restricted Domain
::域和受限制域

Domain is the possible inputs to a function . Many functions allow any kind of numbers to be inputted. This includes numbers that are positive, negative, zero, fractions or decimals. The squaring function $\begin{aligned} y = x^{2} \end{aligned}$ is an example that has a domain of all possible real numbers. Three functions have very specific restrictions:
::域是函数的可能输入。许多函数允许输入任何类型的数字。包括正数、负数、零数、分数或小数数。 y=x2 的方位函数是一个包含所有可能实际数字的域的示例。三个函数有非常具体的限制 :

The square root function : $\begin{aligned} y = \sqrt{x} \end{aligned}$
::平方根函数: y=x

Domain restriction: $\begin{aligned} x \geq 0 \end{aligned}$
::域限制: x#0

This is because the square root of a negative number is not a real number . This restriction can be observed in the graph because the curve ends at the point (0, 0) and is not defined anywhere where $\begin{aligned} x \end{aligned}$ is negative.
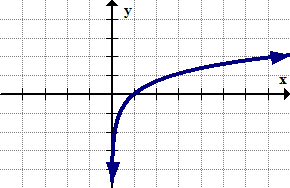
::这是因为负数的平方根不是一个实际数字。此限制可以在图形中观察到, 因为曲线在点( 0, 0) 结束, 而且没有在 x 负的任何地方定义。

The logarithmic function: $\begin{aligned} y = \ln x \end{aligned}$
::对数函数:y=lnx

Domain restriction: $\begin{aligned} x > 0 \end{aligned}$
::域限制: x>0

The log function is only defined on numbers that are strictly bigger than zero. This is because the logarithmic function is a different way of writing exponents. One property of exponents is that any positive number raised to any power will never produce a negative number or zero. The restriction can be observed in the graph by the way the log function approaches the vertical line $\begin{aligned} x = 0 \end{aligned}$ and shoots down to infinity.
::日志函数仅根据严格大于零的数字来定义。这是因为对数函数是一种不同的写引号方式。引号的一个属性是, 任何电源中的任何正数都不会产生负数或零。此限制可以通过日志函数接近垂直线 x=0 和向下射至无限的方式在图形中观察到。

lesson content

The reciprocal function: $\begin{aligned} y = \frac{1}{x} \end{aligned}$
::互惠函数:y=1x

Domain Restriction: $\begin{aligned} x \neq 0 \end{aligned}$
::域限制: x0

The reciprocal function is restricted because you cannot divide numbers by zero. Any $\begin{aligned} x \end{aligned}$ values that make the denominator of a function zero are outside of the domain. This restriction can be observed in the graph by the way the reciprocal function never touches the vertical line $\begin{aligned} x = 0 \end{aligned}$ .
::对应函数是限制的,因为无法将数字除以零。使函数零分母成为函数零分母的任何x值都在域外。对等函数从不触及垂直线x=0时,此限制可以在图表中观察到。

Range
::范围范围范围

Range is the possible outputs of a function. Just about any function can produce any output through the use of transformations and so determining the range of a function is significantly less procedural than determining the domain. Use what you know about the shape of each function and their equations to decide which $\begin{aligned} y \end{aligned}$ values are possible to produce and which $\begin{aligned} y \end{aligned}$ values are impossible to produce.
::范围是函数的可能输出范围。任何函数都可以通过使用变换产生任何输出, 因此确定函数范围的程序远不如确定域。使用您了解的每个函数的形状及其方程式来决定哪些值是可能的,哪些值是无法生成的。

Finding Domain and Range
::查找域域和范围

The domain and range for the graph above are:
::以上图表的域和范围为:

Domain: $\begin{aligned} x \in [- 3, 2] \end{aligned}$
::域名: x[- 3, 2]

Range: $\begin{aligned} y \in [- 2, 3] \end{aligned}$
::范围:y[-2,3]

Note that the $\begin{aligned} \in \end{aligned}$ symbol means “is an element of” and means that the $\begin{aligned} x \end{aligned}$ or the $\begin{aligned} y \end{aligned}$ is in that interval and the numbers in the interval are always written in increasing order . [3, -2] is considered improper.
::请注意 {{{{} 符号意指“是......的一个要素” , 意指 x 或 y 是在那个间隔之内, 而该间隔内的数字总是按不断递增的顺序写。 [3, - 2] 被认为不适当。

Note that even though the [-3, 2] may look similar to the ordered pair that represents the point where $\begin{aligned} x = - 3 \end{aligned}$ and $\begin{aligned} y = 2 \end{aligned}$ , this is not the case. Both the -3 and the 2 are $\begin{aligned} x \end{aligned}$ values. This misconception is why you should always write $\begin{aligned} x \in \end{aligned}$ because it reminds you of this fact. Many people get very confused when they see something like $\begin{aligned} x \in (- 2, 1) \end{aligned}$ because they see the parenthesis and immediately see a point when they should see an interval on the $\begin{aligned} x \end{aligned}$ axis.
::请注意,尽管[ 3, 2] 可能看起来与代表 x3 和 y=2 的点的定购配对相似,但情况并非如此。无论是 - 3 和 2 是 x 值。这是为什么你总是要写 x , 因为它提醒你这个事实。许多人在看到 x ( - 2, 1) 等东西时会非常困惑, 因为他们看到括号, 并立即看到一个点, 当他们在 x 轴上看到一个间隔。

In the graph below, there are two different pieces of the function.
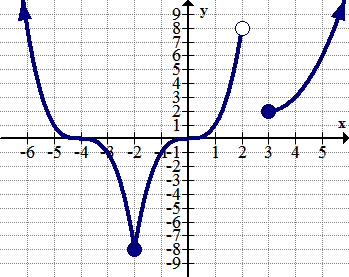
::在下图中,函数有两个不同的部分。

The domain and range for the graph above are:
::以上图表的域和范围为:

Domain: $\begin{aligned} x \in [- 3, - 1) \cup [0, 3) \end{aligned}$
::域 : x[- 3, - 1] [, 3]

Range: $\begin{aligned} y \in [- 2, \infty) \end{aligned}$
::范围: y[- 2, ]

The function seems to approach the vertical line $\begin{aligned} x = - 1 \end{aligned}$ without actually reaching it so an open bracket is used. Also, the empty hole at the point (3, 1) which is why the domain excludes the $\begin{aligned} x \end{aligned}$ value of 3.
::函数似乎在接近垂直线 x1 时没有实际达到它,所以使用了开括号。此外,点(3,1)上的空洞,这就是为什么域排除了3的 x 值。

Examples
::实例

Example 1
::例1

Earlier, you were asked which basic functions have limited domains. The three functions that have limited domains are the square root function, the log function and the reciprocal function. The square root function has a restricted domain because you cannot take square roots of negative numbers and produce real numbers. The log function is restricted because the log function is not defined to operate on non-positive numbers. The reciprocal function is restricted because numbers that are divided by zero are not defined.
::早些时候,有人询问了哪些基本函数有有限的域。三个域有限的函数是平根函数、日志函数和对等函数。正根函数有一个有限的域,因为您无法从负数的平方根中取出正方根并生成真实数字。日志函数是有限的,因为日志函数没有定义以非正数运行。对等函数是有限的,因为除以零的数字没有定义。

Example 2
::例2

Identify the domain and range of the following function written in a table:
::确定表格中写入的下列函数的域和范围:

$\begin{aligned} x \end{aligned}$	$\begin{aligned} y \end{aligned}$
0	5
1	6
2	7
$\begin{aligned} \frac{1}{2} \end{aligned}$	6
$\begin{aligned} π \end{aligned}$	$\begin{aligned} \frac{π}{2} \end{aligned}$

The specific equation of the function may be hidden, but from the table you can determine the domain and range directly from the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values. It may be tempting to guess that other values could potentially work in the table, especially if the pattern is obvious, but this is not the kind of question that asks what the function could be. Instead this question just asks what is the stated domain and range.
::函数的具体方程式可能是隐藏的, 但从表格中您可以确定域名, 并直接从 x 和 y 值中选择。这可能会诱人猜想, 其他值在表格中可能有效, 特别是如果模式是显而易见的, 但这不是问函数可能是什么的问题。相反, 这个问题只是问指定域名和范围是什么。

Domain: $\begin{aligned} x \in {0, 1, 2, \frac{1}{2}, π} \end{aligned}$
::域名: x0,1,2,12,

Range: $\begin{aligned} y \in {5, 6, 7, \frac{π}{2}} \end{aligned}$
::范围:y 5,6,7,2}

Notice that the two 6’s that appear in the table do not need to be written twice in the range.
::请注意,表中出现的两张6 ' s,不必在幅度内写两次。

Example 3
::例3

Identify the domain of the following three transformed functions.
::确定以下三个转变功能的域名。

$\begin{aligned} y = 10 \sqrt{2 - x} - 3 \end{aligned}$
::y=102-x-3

The argument of the function must be greater than or equal to 0.
::函数的参数必须大于或等于 0。

\begin{aligned} 2 - x & \geq 0 \\ - x & \geq - 2 \\ x & \leq 2 \end{aligned}

::2 -x=0 -x==2x=2

Domain: $\begin{aligned} x \in (- \infty, 2] \end{aligned}$
::域名: x(),2;

$\begin{aligned} y = \frac{3 x}{x^{2} + 7 x + 12} \end{aligned}$
::y=3x22+7x+12

The denominator cannot be equal to 0. First find what values of $\begin{aligned} x \end{aligned}$ would make it equal to zero and then you can exclude those values.
::分母不能等于 0。首先找到 x 的什么值可以使其等于零, 然后您可以排除这些值。

\begin{aligned} x^{2} + 7 x + 12 & = 0 \\ (x + 4) (x + 3) & = 0 \\ x & = - 4, - 3 \end{aligned}

::x2+7x+12=0(x+4)(x+3)=0x4-3

Domain: $\begin{aligned} x \in (- \infty, - 4) \cup (- 4, - 3) \cup (- 3, \infty) \end{aligned}$
::域 : x ,

$\begin{aligned} y = - 4 \ln (3 x - 9) + 11 \end{aligned}$
::y4ln( 3x- 9) +11

The argument must be strictly greater than 0.
::论据必须严格大于0。

\begin{aligned} 3 x - 9 & > 0 \\ 3 x & > 9 \\ x & > 3 \end{aligned}

::3x-9>03x>9x>3

Domain: $\begin{aligned} x \in (3, \infty) \end{aligned}$
::域 : x( 3, )

Example 4
::例4

What is the domain and range of the sine wave?
::什么是正弦波的域和范围?

Domain: $\begin{aligned} x \in (- \infty, \infty) \end{aligned}$
::域 : x(,)

Range: $\begin{aligned} y \in [- 1, 1] \end{aligned}$
::范围:y[- 1,1]

Summary

Domain and range are described in interval notation, with parentheses meaning non-inclusive and brackets [ ] meaning inclusive.
::域和范围以间距符号表示,括号()是指非包容性的,括号[ ]是指包容性的。

Domain refers to the possible inputs of a function,
::域是指函数、函数、函数、函数、函数、函数和函数可能的投入。

Range refers to the possible outputs of a function.
::范围指函数的可能输出。

To find the domain and range of a graph, observe the intervals on the x-axis (domain) and y-axis (range) where the function is defined.
::要找到图形的域和范围,请在函数定义的 x 轴( 域) 和 Y 轴( 范围) 上观察间隔。

The "is an element of" symbol (∈) is used to indicate that a value is within a specific interval, and intervals should always be written in increasing order.
::“ 是” 符号的一个元素, 用来表示值在特定间隔之内, 间隔应该总是按增加的顺序写。

Review
::回顾

Convert the following descriptions of numbers into interval notation.
::将以下数字描述转换为间隔符号。

1. All positive numbers not including 0.
::1. 所有正数不包括0。

2. Every number between -1 and 1 including -1 but not 1.
::2. -1至1之间的每一数字,包括-1,但不包括1。

3. Every number between 1 and 5 not including 2 or 3, but including 1 and 5.
::3. 1至5之间的每一数字不包括2或3,但包括1和5。

4. Every number greater than 5, not including 5.
::4. 每超过5个,但不包括5个。

5. All real numbers except 1.
::5. 除1外,所有实际数字。

Translate the following inequalities into interval notation.
::将以下不平等转换为间隙符号。

6. $\begin{aligned} - 4 < x \leq 5 \end{aligned}$
::6.-4<x=5

7. $\begin{aligned} x > 0 \end{aligned}$
::7. x>0

8. $\begin{aligned} - \infty < x \leq 4 o r 5 < x < \infty \end{aligned}$
::8. x4或5<x1或5<_BAR_

Find the domain and range of each graph below.
::查找下方每个图表的域和范围。

10.

Given the stated domain and range, draw a possible graph.
::根据指定的域和范围,绘制一个可能的图表。

11. Domain: $\begin{aligned} x \in [0, \infty) \end{aligned}$ Range: $\begin{aligned} y \in (- 2, 2] \end{aligned}$
::11. 域: x[0,] 范围:y(-2,2)

12. Domain: $\begin{aligned} x \in [- 4, 1) \cup (1, \infty) \end{aligned}$ Range: $\begin{aligned} y \in (- \infty, \infty) \end{aligned}$
::12. 域 : x[- 4,1,1,1,1, ] 范围 : y( , )

13. Given the table, find the domain and range.
::13. 根据表格,找到域和范围。

$\begin{aligned} x \end{aligned}$	$\begin{aligned} y \end{aligned}$
-2	7
3	7
2	1
$\begin{aligned} \frac{3}{4} \end{aligned}$	5
$\begin{aligned} \frac{π}{2} \end{aligned}$	$\begin{aligned} π \end{aligned}$

Find the domain for the following functions using interval notation.
::使用间距符号查找下列函数的域。

14. $\begin{aligned} y = - 3 \sqrt{x + 4} - 1 \end{aligned}$
::14. y3x+4-1

15. $\begin{aligned} y = \frac{7}{x + 6} - 1 \end{aligned}$
::15.y=7x+6-1

16. $\begin{aligned} y = 5 \ln (x^{2} - 1) + 4 \end{aligned}$
::y=5ln(x2-1)+4

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

域和范围

Domain and Range ::域和范围

Notation ::标注

Domain and Restricted Domain ::域和受限制域

Range ::范围范围范围

Finding Domain and Range ::查找域域和范围

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)