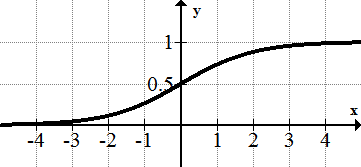1.6 对称

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 对对称

  Collapse Expand

  对对称

  播放段落

  Some functions, like the sine function , the absolute value function and the squaring function, have reflection across the line $\begin{align*}x=0\end{align*}$ . Other functions like the cubing function and the reciprocal function have rotational symmetry about the origin. 
  ::有些函数,如正弦函数、绝对值函数和对称函数,在线性=0之间反射。其他函数,如幼体函数和对等函数,则对源值进行旋转对称。

  播放段落

  Why is the first group categorized as even functions while the second group is categorized as odd functions? 
  ::为什么第一组被归类为偶数职能,而第二组则被归类为奇数职能?

  播放段落

  Even and Odd Functions
  ::偶函数和奇函数

  播放段落

  Even Functions
  ::偶偶偶职职函数

  播放段落

  Functions symmetrical across the line $\begin{align*}x=0\end{align*}$ (the  $\begin{align*}y\end{align*}$ axis) are called even. Even functions have the property that when a negative value is substituted for $\begin{align*}x\end{align*}$ , it produces the same value as when the positive value is substituted for the $\begin{align*}x\end{align*}$ . In other words, the equation  $\begin{align*}f(-x)=f(x)\end{align*}$  holds true for even functions.
  ::横跨线x=0(y轴)的函数对称被称为偶数。即使函数也具有以下属性:当负值被X取代时,负值产生的数值与x替代正值时的数值相同。换句话说,公式f(x)=f(x)对等函数也适用。

  播放段落

  To show that the function  $\begin{align*}f(x)=3x^4-5x^2+1\end{align*}$  is even, show that  $\begin{align*}f(-x)=f(x)\end{align*}$ .
  ::要显示函数 f( x) = 3x4- 5x2+1 是偶数, 请显示 f( x) = f( x) 。

  播放段落

  $$\begin{array}{rl}f(-x)& =3(-x{)}^4-5(-x{)}^2+1\\ & =3x^4-5x^2+1\\ & =f(x)\end{array}$$

  $$\begin{align*}f(-x)&=3(-x)^4-5(-x)^2+1\\ &=3x^4-5x^2+1\\ &=f(x)\end{align*}$$
  :-x)=3(-x)4-5(-x)2+1=3x4-5x2+1=5x2+1=f(x)

  播放段落

  The property that both positive and negative numbers raised to an even power are always positive is the reason why the term even is used. It does not matter that the coefficients are even or odd, just the exponents. 
  ::平权的正数和负数都生成了正数和负数的属性总是正数,这是甚至使用该词的原因。 系数是偶数还是奇数并不重要,只是指数而已。

  播放段落

  Odd Functions
  ::奇数函数函数

  播放段落

  Functions that have rotational symmetry about the origin are called odd functions. Odd functions have the property that when a negative  $\begin{align*}x\end{align*}$ value is substituted into the function, it produces a negative version of the function evaluated at a positive value. In other words, the equation $\begin{align*}f(-x)=-f(x)\end{align*}$   holds true for odd functions.
  ::对原函数具有旋转对称函数的函数被称为奇函数。 奇函数的属性是, 当负 x 值被替换为函数时, 它会生成负值函数的负值。 换句话说, 对奇函数来说, 等式f( - x)\\\\\\\f( x) 是正确的 。

  播放段落

  This property becomes increasingly important in problems and proofs of Calculus and beyond, but for now it is sufficient to identify functions that are even, odd or neither and show why. 
  ::这种财产在微积分问题和证据中及以后变得越来越重要,但现在只要确定偶数、奇数或两者兼而有之的功能并表明原因就足够了。

  播放段落

  To show that $\begin{align*}f(x)=4x^3-x\end{align*}$  is odd, show that   $\begin{align*}f(-x)=-f(x)\end{align*}$ .
  ::要显示 f( x) = 4x3- x 是奇数, 请显示 f( x)\\\\ f( x) 。

  播放段落

  $$\begin{array}{rl}f(-x)& =4(-x{)}^3-x\\ & =-4x^3-x\\ & =-(4x^3+x)\\ & =-f(x)\end{array}$$

  $$\begin{align*}f(-x)&=4(-x)^3-x\\ &=-4x^3-x\\ &=-(4x^3+x)\\ &=-f(x)\end{align*}$$
  :- x) = 4(- x) 3 - x4x3- x) ( 4x3+x) f( x)

  播放段落

  Just like even functions are named, odd functions are named because negative signs don’t disappear and can always be factored out of odd functions. 
  ::也因为负面信号不会消失, 总是可以从奇异功能中考虑。

  播放段落

  Even and odd functions describe different types of symmetry, but both derive their name from the properties of exponents. A negative number raised to an even number will always be positive. A negative number raised to an odd number will always be negative. 
  ::偶数函数和奇数函数描述不同类型的对称,但两者都取自推算符的属性。 以偶数表示的负数总是正数。 以奇数表示的负数总是负数。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Which of the basic functions are even, which are odd and which are neither? 
  ::哪些基本功能是偶数,哪些功能是奇数,哪些功能不是偶数?

  播放段落

  Even Functions: The squaring function and the absolute value function.
  ::偶数函数:分数函数和绝对值函数。

  播放段落

  Odd Functions: The identity function, the cubing function, the reciprocal function, the sine function.
  ::奇数函数: 身份功能、 幼稚功能、 互惠功能、 正弦功能 。

  播放段落

  Neither: The square root function , the exponential function and the log function. The logistic function is also neither because it is rotationally symmetric about the point  $\begin{align*}\left(0, \frac{1}{2}\right)\end{align*}$  as opposed to the origin.
  ::均不: 平方根函数、 指数函数和日志函数。 后勤函数也不相同, 因为它对点( 0, 12) 相对于源值是旋转对称的 。

  

  播放段落

  Example 2
  ::例2

  播放段落

  Suppose $\begin{align*}h(x)\end{align*}$  is an even function and $\begin{align*}g(x)\end{align*}$  is an odd function. $\begin{align*}f(x)=h(x)+g(x). \end{align*}$  Is $\begin{align*}f(x)\end{align*}$  even or odd? If $\begin{align*}h(x)\end{align*}$ is even then $\begin{align*}h(-x)=h(x)\end{align*}$ . If $\begin{align*}g(x)\end{align*}$ is odd then $\begin{align*}g(-x)=-g(x)\end{align*}$ . 
  ::假设 h( x) 是偶数函数, g( x) 是奇数函数 。 f( x) =h( x)+g( x) 。 f( x) 是偶数还是奇数? 如果h( x) 是偶数, h( x) =h( x) 。 g( x) 是奇数, g( x)\g( x) 。

  播放段落

  Therefore : $\begin{align*}f(-x)=h(-x)+g(-x)=h(x)-g(x)\end{align*}$
  ::因此:f(-x)=h(-x)+g(-x)=h(x)-g(x)

  播放段落

  This does not match $\begin{align*}f(x)= h(x)+g(x)\end{align*}$  nor does it match $\begin{align*}-f(x)=-h(x)-g(x)\end{align*}$ . 
  ::此不匹配 f( x) =h( x) +g( x) , 也不匹配 - f( x) \\\ h( x) - g( x) 。

  播放段落

  This is a proof that shows the sum of an even function and an odd function will never itself be even or odd. 
  ::这是显示偶数函数和奇数函数之和的证据, 奇数函数本身永远不会是偶数或奇数 。

  播放段落

  Example 3
  ::例3

  播放段落

  Determine whether the following function is even, odd, or neither. 
  ::确定以下函数是偶数、奇数还是偶数。

  播放段落

  $\begin{align*}f(x)=x(x^2-1)(x^4+1)\end{align*}$
  :xx) =x(x2- 1)(x4+1)

  播放段落

  Identify whether the function is even, odd or neither and explain why.
  ::确定该函数是偶数、奇数还是非偶数,并解释原因。

  播放段落

  $$\begin{align*}f(x)&=x(x^2-1)(x^4+1)\\ f(-x)&= (-x)((-x)^2-1)((-x)^4+1)\\ &=-x(x^2-1)(x^4+1)\\ &=-f(x)\end{align*}$$
  :x) =x(x2- 1)(x4+1) f(x) =(x)(x) (-x)(x) 2-1 ((-x) 4+1) x(x2- 1)(x4+1)(x4+1) ** f(x)

  播放段落

  The function is odd because  $\begin{align*}f(-x)=-f(x)\end{align*}$  holds true.
  ::函数是奇数, 因为 f(- x)\\\\\\\f( x) 仍然正确 。

  播放段落

  $\begin{align*}f(x)=4x^3-|x|\end{align*}$
  :xx) = 4x3

  播放段落

  $$\begin{array}{rl}f(-x)& =4(-x{)}^3-x\\ & =-4x^3-x\end{array}$$

  $$\begin{align*}f(-x)&=4(-x)^3-x\\ &=-4x^3-x\end{align*}$$
  :- x) = 4(- x) 3 - x= 4x4x3 - x)

  播放段落

  This does not seem to match either $\begin{align*}f(x)=4x^3-|x|\end{align*}$  or $\begin{align*}-f(x)=-4x^3+|x|\end{align*}$ . Therefore, this function is neither even nor odd. 
  ::此函数似乎既不匹配 f( x) = 4x3 {x}} 也不匹配 f( x) = 4x3} {x} 或 - f( x) = 4x3} {x} 。 因此, 此函数既不是偶数也不是奇数 。

  播放段落

  Note: This function is a difference of an odd function and an even function. This should be a clue that the resulting function is neither even nor odd. 
  ::注意: 此函数是奇函数和偶函数的区别。 这应该是一个提示, 由此得出的函数既不是奇函数,也不是奇函数。

  Summary

  播放段落 Even functions are symmetric across the y-axis and have the property that $\begin{align*}f(-x) = f(x).\end{align*}$   ::连函数也横跨 Y 轴,具有 f( - x) = f( x) 的属性。 播放段落 Odd functions have rotational symmetry about the origin and have the property that $\begin{align*}f(-x) = -f(x).\end{align*}$   ::Odd 函数对源有旋转的对称, 属性为 f( x)\\\\ f( x) 。

  播放段落

  Review
  ::回顾

  播放段落

  Determine whether the following functions are even, odd, or neither.
  ::确定下列函数是偶数、奇数还是均值。

  播放段落

  1. $\begin{align*}f(x)=-4x^2+1\end{align*}$
  ::1. f(x)4x2+1

  播放段落

  2. $\begin{align*}g(x)=5x^3-3x\end{align*}$
  ::2. g(x)=5x3-3-3x

  播放段落

  3.  $\begin{align*}h(x)=2x^2-x\end{align*}$
  ::3. h(x)=2x2-x

  播放段落

  4. $\begin{align*}j(x)=(x-4) (x-3)^3\end{align*}$
  ::4. j(x)=(x-4)(x-3)3

  播放段落

  5.  $\begin{align*}k(x)=x(x^2-1)^2\end{align*}$
  ::5. k(x)=x(x2-1)2

  播放段落

  6.  $\begin{align*}f(x)=2x^3-5x^2-2x+1\end{align*}$
  ::6. f(x)=2x3-5x2-2-2x+1

  播放段落

  7.  $\begin{align*}g(x)=2x^2-4x+2\end{align*}$
  ::7. g(x)=2x2-4x+2

  播放段落

  8.  $\begin{align*}h(x)=-5x^4+x^2+2\end{align*}$
  ::8. h(x) 5x4+x2+2

  播放段落

  9. Suppose $\begin{align*}h(x)\end{align*}$ is even and $\begin{align*}g(x)\end{align*}$  is odd. Show that $\begin{align*}f(x)=h(x)-g(x)\end{align*}$  is neither even nor odd.
  ::9. 假设h(x)是偶数,g(x)是奇数。显示 f(x)=h(x)-g(x)既不是偶数,也不是奇数。

  播放段落

  10. Suppose  $\begin{align*}h(x)\end{align*}$ is even and $\begin{align*}g(x)\end{align*}$  is odd. Show that $\begin{align*}f(x)=\frac{h(x)}{g(x)}\end{align*}$  is odd.
  ::10. 假设h(x)是偶数,g(x)是奇数。显示 f(x)=h(x)g(x)是奇数。

  播放段落

  11. Suppose $\begin{align*}h(x)\end{align*}$ is even and $\begin{align*}g(x)\end{align*}$  is odd. Show that $\begin{align*}f(x)=h(x) \cdot g(x)\end{align*}$  is odd.
  ::11. 假设h( x) 是偶数, g( x) 是奇数。 显示 f( x) =h( x) =g( x) 是奇数 。

  播放段落

  12. Is the sum of two even functions always an even function? Explain.
  ::12. 两个偶数函数的总和是否总是一个偶数函数?

  播放段落

  13. Is the sum of two odd functions always an odd function? Explain.
  ::13. 两个奇数函数的总和是否总是奇数函数?

  播放段落

  14. Why are some functions neither even nor odd?
  ::14. 为什么有些功能甚至既不奇怪,也不奇怪?

  播放段落

  15. If you know that a function is even or odd, what does that tell you about the symmetry of the function?
  ::15. 如果你知道一个函数是偶数或奇数,那你对函数的对称性有什么看法?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。