Course: 1.7 增长和减少 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

增长和减少

It is important to be able to distinguish between when functions are increasing and when they are decreasing. In business this could mean the difference between making money and losing money. In physics it could mean the difference between speeding up and slowing down.
::重要的是能够区分功能增长的时间和功能下降的时间。在商业领域,这可能意味着赚钱和亏损之间的差别。在物理学领域,这可能意味着加速和减速之间的差别。

How do you decide when a function is increasing or decreasing?
::您如何决定一个函数何时在增加或减少?

Increasing and Decreasing Functions
::增加和减少函数

Increasing means places on the graph where the slope is positive.
::增长是指在图中斜坡为正值的位置。

The formal definition of an increasing interval is: an open interval on the $\begin{aligned} x \end{aligned}$ axis of $\begin{aligned} (a, d) \end{aligned}$ where every $\begin{aligned} b, c \in (a, d) \end{aligned}$ with $\begin{aligned} b < c \end{aligned}$ has $\begin{aligned} f (b) \leq f (c) \end{aligned}$ .
::增加间隔的正式定义是:在(a,d)x轴上的开放间隔,其中,与(a,d)b,c,(a,d)和(b)<c的轴有f(b)f(c)。

A interval is said to be strictly increasing if $\begin{aligned} f (b) < f (c) \end{aligned}$ is substituted into the definition.
::如果将f(b) <f(c)替换为定义,则时间间隔将严格增加。

Decreasing means places on the graph where the slope is negative. The formal definition of decreasing and strictly decreasing are identical to the definition of increasing with the inequality sign reversed.
::下降意味着在图中斜坡为负值的位置下降。正式的递减和严格递减的定义与增加的定义相同,不平等标志被颠倒。

A function is called monotonic if the function only goes in one direction and never switches between increasing and decreasing.
::如果函数只朝一个方向前进,而从不在增加和减少之间交换,则该函数被称为单声道。

Out of the basic functions, the monotonically increasing functions are:
::在基本职能中,单质增加的职能是:

$\begin{aligned} f (x) = x, f (x) = x^{3}, f (x) = \sqrt{x}, f (x) = e^{x}, f (x) = \ln x, f (x) = \frac{1}{1 + e^{- x}} \end{aligned}$
:xx)=xx,f(x)=x3,f(x)=x,f(x)=x,f(x)=ex,f(x)=ln=x,f(x)=11+e-x

The only basic functions that are not monotonically increasing are:
::唯一不单质增加的基本功能是:

$\begin{aligned} f (x) = x^{2}, f (x) = | x |, f (x) = \frac{1}{x}, f (x) = \sin x \end{aligned}$
:xx) =x2,f(x) x,f(x) =1x,f(x) =sinx

Identifying analytically where functions are increasing and decreasing often requires Calculus. For PreCalculus, it will be sufficient to be able to identify intervals graphically and through your knowledge of what the parent functions look like.
::分析确定哪些功能在增加和减少,往往需要计算。对于计算前,只需能够用图形方式和通过了解母函数的外观来识别间隔即可。

Examples
::实例

Example 1
::例1

Earlier, you were asked how to determine if a function is increasing or decreasing. Increasing is where the function has a positive slope and decreasing is where the function has a negative slope. A common misconception is to look at the squaring function and see two curves that symmetrically increase away from zero. Instead, you should always read functions from left to right and draw slope lines and decide if they are positive or negative.
::早些时候,有人问您如何确定函数在增加或减少。增加是指函数有正斜度, 递减是指函数有负斜度。一个常见的错误观念是看分角函数,看两条曲线,两条曲线从零成对地增加。相反, 您应该总是从左到右读函数, 并绘制斜线, 决定这些函数是正的还是负的。

Example 2
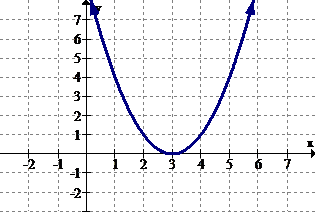
::例2

Estimate where the following function is increasing and decreasing.
::估计下列职能在哪些方面在增加和减少。

Increasing: $\begin{aligned} x \in (- \infty, - 1.5) \cup (1.5, \infty) \end{aligned}$ .
::增加: x(,-1.5)(1.5,)。

Decreasing: $\begin{aligned} x \in (- 1.5, 1.5) \end{aligned}$
::下降: x(-1.5,1.5)

Example 3
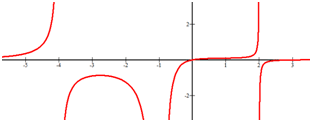
::例3

Estimate where the following function is increasing and decreasing.
::估计下列职能在哪些方面在增加和减少。

Increasing $\begin{aligned} x \in (- \infty, - 4) \cup (- 4, - 2.7) \cup (- 1, 2) \cup (2, \infty) \end{aligned}$ .
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

Decreasing $\begin{aligned} x \in (- 2.7, - 1) \end{aligned}$
::衰减(- 2.7,-1)

Example 4
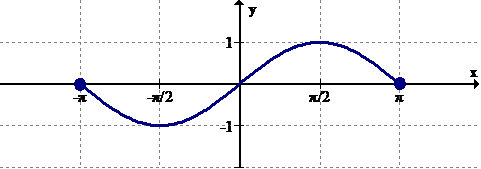
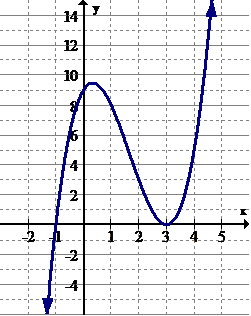
::例4

Estimate the intervals where the function is increasing and decreasing.
::估计该职能在增加和减少的间隔。

Increasing: $\begin{aligned} x \in (- \infty, - 4) \cup (- 2, 1.5) \end{aligned}$
::增加: x(),- 4) (− 2,1.5)

Decreasing: $\begin{aligned} x \in (- 4, - 2) \cup (1.5, \infty) \end{aligned}$
::衰减: x( - 4, - 2) ( 1. 5, )

Notice that open intervals are used because at $\begin{aligned} x = - 4, - 2, 1.5 \end{aligned}$ the slope of the function is zero. This is where the slope transitions from being positive to negative. The reason why open parentheses are used is because the function is not actually increasing or decreasing at those specific points.
::提醒使用开放间隔是因为在 x4, 2- 2, 1. 5 函数的斜度为零。这是斜度从正向负向正向负的过渡。使用打开括号的原因是, 函数在这些特定点上没有实际增加或减少。

Example 5
::例5

A continuous function has a global maximum at the point (3, 2), a global minimum at (5, -12) and has no relative extrema or other places with a slope of zero. What are the increasing and decreasing intervals for this function?
::连续函数在点(3,2)上具有全球最高值(3,2),在点(5,12)上具有全球最低值(5,12),没有相对的外形或其他斜度为零的地方。这一函数的增减间隔是多少?

Increasing $\begin{aligned} x \in (- \infty, 3) \cup (5, \infty) \end{aligned}$ .
::增加 x(, 3) ( 5, ) 。

Decreasing $\begin{aligned} x \in (3, 5) \end{aligned}$
::衰减 x( 3, 5)

Note: The $\begin{aligned} y \end{aligned}$ coordinates are not used in the intervals. A common mistake is to want to use the $\begin{aligned} y \end{aligned}$ coordinates.
::注:在间隔中不使用 Y 座标。常见错误是想要使用 y 座标。

Summary

Functions are increasing on a given interval if it has a positive slope on that interval.
::功能如果在某一间隔内有正斜度,则在某一间隔内增加。

Functions are decreasing on a given interval if it has a negative slope on that interval.
::如果功能在某一间隔上有负斜度,则该间隔的功能在某一间隔内递减。

A function is called monotonic if it only goes in one direction and never switches between increasing and decreasing.
::函数如果只朝一个方向前进,而从不在增加和减少之间交换,则称为单音函数。

Review
::回顾

Use the graph below for 1-2.
::1-2使用下图。

1. Identify the intervals (if any) where the function is increasing.
::1. 确定职能增加的间隔(如果有的话)。

2. Identify the intervals (if any) where the function is decreasing.
::2. 确定职能减少的间隔(如果有的话)。

Use the graph below for 3-4.
::3-4使用下图。

3. Identify the intervals (if any) where the function is increasing.
::3. 确定职能增加的间隔(如果有的话)。

4. Identify the intervals (if any) where the function is decreasing.
::4. 确定职能减少的间隔(如果有的话)。

Use the graph below for 5-6.
::5-6使用下图。

5. Identify the intervals (if any) where the function is increasing.
::5. 确定职能增加的间隔(如果有的话)。

6. Identify the intervals (if any) where the function is decreasing.
::6. 确定职能减少的间隔(如果有的话)。

Use the graph below for 7-8.
::7-8使用下图。

7. Identify the intervals (if any) where the function is increasing.
::7. 确定职能增加的间隔(如果有的话)。

8. Identify the intervals (if any) where the function is decreasing.
::8. 确定职能减少的间隔(如果有的话)。

Use the graph below for 9-10.
::9-10使用下图。

9. Identify the intervals (if any) where the function is increasing.
::9. 确定职能增加的间隔(如果有的话)。

10. Identify the intervals (if any) where the function is decreasing.
::10. 确定职能减少的间隔(如果有的话)。

11. Give an example of a monotonically increasing function.
::11. 举一个单一增长功能的例子。

12. Give an example of a monotonically decreasing function.
::12. 举一例说明单质递减功能。

13. A continuous function has a global maximum at the point (1, 4), a global minimum at (3, -6) and has no relative extrema or other places with a slope of zero. What are the increasing and decreasing intervals for this function?
::13. 连续函数在点(1,4)上具有全球最高值,在点(3,6)上具有全球最低值(3,6),没有相对的外形或斜度为零的其他位置。

14. A continuous function has a global maximum at the point (1, 1) and has no other extrema or places with a slope of zero. What are the increasing and decreasing intervals for this function?
::14. 连续函数在点(1,1)上具有全球最高值,没有其它偏差或斜度为零的地点。这一函数的增减间隔是多少?

15. A continuous function has a global minimum at the point (5, -15) and has no other extrema or places with a slope of zero. What are the increasing and decreasing intervals for this function?
::15. 连续功能在点(5,15)上具有全球最低值,没有其它偏差或零度斜度偏差的地方。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

增长和减少

Increasing and Decreasing Functions ::增加和减少函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)