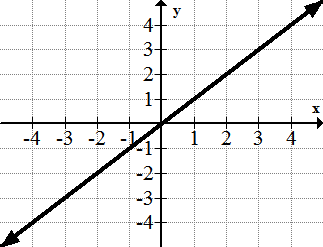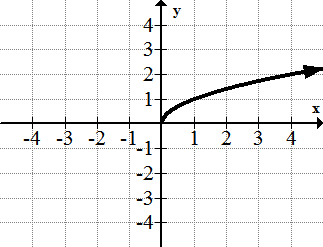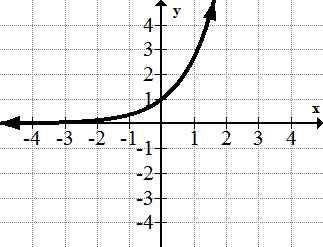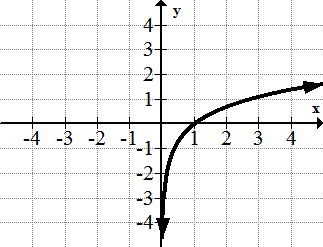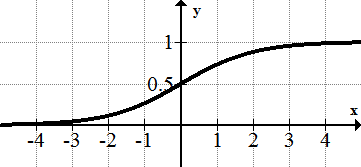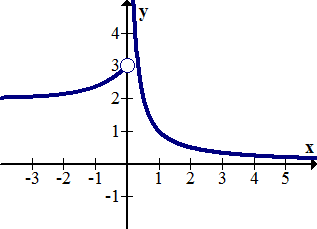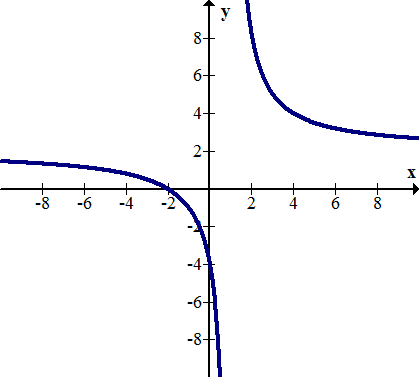Course: 1.9 零星和结束行为

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

零星和结束行为

Most functions continue beyond the viewing window in our calculator or computer. People often draw an arrow next to a dotted line to indicate the pattern specifically. How can you recognize these asymptotes ?

Asymptotes and End Behavior of Functions
::函数的零星和结束行为

A vertical asymptote is a vertical line such as $\begin{aligned} x = 1 \end{aligned}$ that indicates where a function is not defined and yet gets infinitely close to.
::垂直无线线是一个垂直线条,如 x=1, 显示函数没有定义的位置, 但却远近无穷。

A horizontal asymptote is a horizontal line such as $\begin{aligned} y = 4 \end{aligned}$ that indicates where a function flattens out as $\begin{aligned} x \end{aligned}$ gets very large or very small. A function may touch or pass through a horizontal asymptote.
::水平单点是一个水平线, 如 y=4 , 表示函数在 x 变大或变小时的平坦位置。函数可以触摸或通过水平单点。

The reciprocal function has two asymptotes, one vertical and one horizontal. Most computers and calculators do not draw the asymptotes and so they must be inserted by hand as dotted lines.
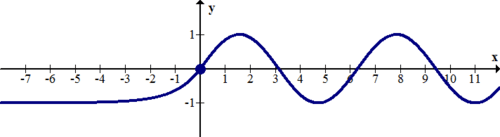
::互惠函数有两个小数点, 一个垂直, 一个水平。大多数计算机和计算器不绘制小数点, 因此它们必须用手插入作为虚线。

Many students have the misconception that an asymptote is a line that a function gets infinitely close to but does not touch. This is not true. Take the following function:
::许多学生有这样的错误观念,即小数线是一个函数无限接近但不触动的线条。这不是真的。请选择以下函数:

The graph appears to flatten as $\begin{aligned} x \end{aligned}$ grows larger. Thus, the horizontal asymptote is $\begin{aligned} y = 0 \end{aligned}$ even though the function clearly passes through this line an infinite number of times.
::当 x 变大时, 图似乎会平滑。因此, 水平的零位为 y=0, 即使函数明显通过此线, 次数无限。

The reason why asymptotes are important is because when your perspective is zoomed way out, the asymptotes essentially become the graph.
::细微粒子之所以重要是因为当你的视角被缩放出去时微粒子基本上变成了图形

To find the asymptotes and end behavior of the function below, examine what happens to $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ as they each increase or decrease.
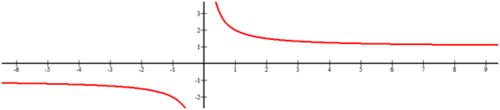
::要找到以下函数的微量和末端行为, 检查 x 和 y 如何随它们各自增减而变化。

The function has a horizontal asymptote $\begin{aligned} y = 2 \end{aligned}$ as $\begin{aligned} x \end{aligned}$ approaches negative infinity. There is a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ . The right hand side seems to decrease forever and has no asymptote.
::当 x 接近负无穷时, 此函数具有水平等量 y= 2 的函数。 x=0 有垂直等量。右手侧似乎会永久缩小, 没有等量。

Note that slant asymptotes do exist and are called .
::请注意,倾斜的微粒确实存在,并被称作。

Examples
::实例

Example 1
::例1

Earlier, you were asked how to identify asymptotes on a graph. Asymptotes written by hand are usually identified with dotted lines next to the function that indicate how the function will behave outside the viewing window. The equations of these vertical and horizontal dotted lines are of the form $\begin{aligned} x = \underline{} \end{aligned}$ and $\begin{aligned} y = \underline{} \end{aligned}$ . When problems ask you to find the asymptotes of a function, they are asking for the equations of these horizontal and vertical lines.
::早些时候,有人询问您如何在图形中识别 asymptotes 。手写的 asymptotes 通常在函数旁边用虚线来识别, 以显示函数在视图窗口外的运行方式。这些垂直和水平点线的方程式是窗体 x 和 y 。当问题要求您找到函数的 asymptotes 时, 他们会询问这些水平线和垂直线的方程式。

Example 2
::例2

Identify the of the following function.
::确定以下职能。

There is a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ gets infinitely small, there is a horizontal asymptote at $\begin{aligned} y = - 1 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ gets infinitely large, there is another horizontal asymptote at $\begin{aligned} y = 1 \end{aligned}$ .
::在 x=0 时有一个垂直的单点。当 x 变得无限小时, 在 y1 时有一个水平的单点。当 x 变得无限大时, 在 y=1 时还有一个水平的单点。

Example 3
::例3

Identify the horizontal and vertical asymptotes of the following function.
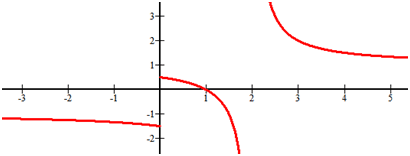
::识别以下函数的水平和垂直小数点。

There is a vertical asymptote at $\begin{aligned} x = 2 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ gets infinitely small there is a horizontal asymptote at $\begin{aligned} y = - 1 \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ gets infinitely large, there is a horizontal asymptote at $\begin{aligned} y = 1 \end{aligned}$ .
::在 x=2 处有一个垂直的单点。当 x 变得无限小时, 在 y1 处有一个水平的单点点。当 x 变得无限大时, 在 y=1 处有一个水平的单点点点。

Example 4
::例4

Identify the horizontal and vertical asymptotes of the following piecewise function:
::识别以下片段函数的水平和垂直单位数 :

$\begin{aligned} f (x) = {\begin{cases} e^{x} - 1 & x \leq 0 \\ \sin x & 0 < x \end{cases} \end{aligned}$
:x)\\\ ex- 1x0sin\\ x0 <x)

There is a horizontal asymptote at $\begin{aligned} y = - 1 \end{aligned}$ as $\begin{aligned} x \end{aligned}$ gets infinitely small. This is because $\begin{aligned} e \end{aligned}$ raised to the power of a very small number becomes 0.000000... and basically becomes zero.
::在 y1 上有一个水平的空位, 因为 x 变得无限小。这是因为 e 升到一个非常小的数的功率成为 0.000000... 并且基本上变成零。

Example 5
::例5

Identify the asymptotes and end behavior of the following function.
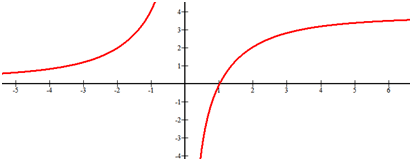
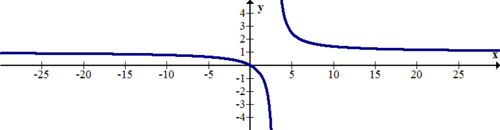
::识别以下函数的微量和末端行为。

There is a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ . The end behavior of the right and left side of this function does not match. The horizontal asymptote as $\begin{aligned} x \end{aligned}$ approaches negative infinity is $\begin{aligned} y = 0 \end{aligned}$ and the horizontal asymptote as $\begin{aligned} x \end{aligned}$ approaches positive infinity is $\begin{aligned} y = 4 \end{aligned}$ . At this point you can only estimate these heights because you were not given the function or the tools to find these values analytically.
::在 x=0 时有一个垂直的单点。此函数的右侧和左侧的末端行为不匹配。 x 接近负无穷度时的水平性单点为y=0, x 接近正无穷度时的水平性单点为 y=4。在这一点上,您只能估计这些高度,因为您没有给您函数或工具来分析查找这些值。

Summary

Vertical asymptotes are lines that indicate where a function is not defined but gets infinitely close to.
::垂直线条为垂直线条,显示函数没有定义,但远近无穷。

Horizontal asymptotes are lines that indicate where a function flattens out as the input gets very large or very small.
::水平负负数是直线,显示输入变得非常大或非常小时函数平坦到哪里。

To find asymptotes and end behavior of a function, examine what happens to the function as the input increases or decreases.
::要找到函数的微量和结束行为, 请检查输入增加或减少后该函数会发生什么后果。

Review
::回顾

Identify the asymptotes and end behavior of the following functions.
::识别下列函数的微量和末端行为。

1. $\begin{aligned} y = x \end{aligned}$
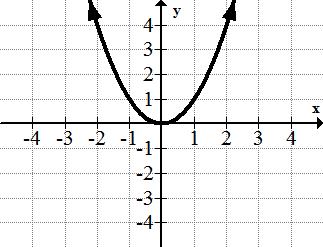
::1.y=x

2. $\begin{aligned} y = x^{2} \end{aligned}$
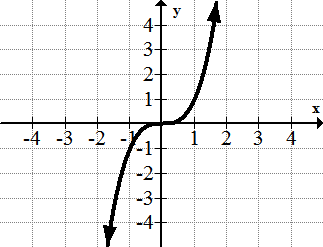
::2. y=x2

3. $\begin{aligned} y = x^{3} \end{aligned}$
::3. y=x3

4. $\begin{aligned} y = \sqrt{x} \end{aligned}$
::4.y=x

5. $\begin{aligned} y = \frac{1}{x} \end{aligned}$
::5. y=1x

6. $\begin{aligned} y = e^{x} \end{aligned}$
::6. y=ex

7. $\begin{aligned} y = \ln (x) \end{aligned}$
::7.y=ln(x)

8. $\begin{aligned} y = \frac{1}{1 + e^{- x}} \end{aligned}$
::8. y=11+e-x

10.

11.

12. Vertical asymptotes occur at $\begin{aligned} x \end{aligned}$ values where a function is not defined. Explain why it makes sense that $\begin{aligned} y = \frac{1}{x} \end{aligned}$ has a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ .
::12. 在未定义函数的 x 值时发生垂直的单位数。解释为什么y=1x在 x=0 时有一个垂直的单位数是有道理的。

13. Vertical asymptotes occur at $\begin{aligned} x \end{aligned}$ values where a function is not defined. Explain why it makes sense that $\begin{aligned} y = \frac{1}{x + 3} \end{aligned}$ has a vertical asymptote at $\begin{aligned} x = - 3 \end{aligned}$ .
::13. 在未定义函数的 x 值时会出现垂直的单位数。解释为什么y= 1x+3 在 x @ 3 时有一个垂直的单位数是有道理的。

14. Use the technique from the previous problem to determine the vertical asymptote for the function $\begin{aligned} y = \frac{1}{x - 2} \end{aligned}$ .
::14. 使用上一个问题的技术来确定函数y=1x-2的垂直静态。

15. Use the technique from problem #13 to determine the vertical asymptote for the function $\begin{aligned} y = \frac{2}{x + 4} \end{aligned}$ .
::15. 使用问题13的技术确定函数y=2x+4的垂直空点。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

零星和结束行为

Asymptotes and End Behavior of Functions ::函数的零星和结束行为

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)