2.9 垂直静态

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 垂直单位数

  Collapse Expand

  垂直单位数

  播放段落

  The basic rational function $\begin{array}{r}f(x)=\frac{1}{x}\end{array}$  is a with a vertical asymptote at $\begin{array}{r}x=0\end{array}$ .  More complicated rational functions may have multiple vertical asymptotes .  These asymptotes are very important characteristics of the function just like holes.  Both holes and vertical asymptotes occur at  $\begin{array}{r}x\end{array}$ values that make the denominator of the function zero.  A driving question is: what makes vertical asymptotes different from holes? 
  ::基本理性函数f( x) = 1x 是带有垂直 asymptote atx=0 的垂直 asymptote 函数。 更复杂的理性函数可能有多个垂直 asymptotes 。 这些 asymptotes 是函数的非常重要的特性, 就像洞一样。 洞和垂直的 asymptotes 都出现在使函数零分母成为 x 值的 x 值上 。 驱动问题在于: 是什么使垂直的静态与洞不同?

  播放段落

  Finding Vertical Asymptotes
  ::寻找垂直的单位数

  播放段落

  Vertical asymptotes occur when a factor of the denominator of a rational expression does not cancel with a factor from the numerator.  When you have a factor that does not cancel, instead of making a hole at that  $\begin{array}{r}x\end{array}$ value, there exists a vertical asymptote.  The vertical asymptote is represented by a dotted vertical line.  Most calculators will not identify vertical asymptotes and some will incorrectly draw a steep line as part of a function where the asymptote actually exists. 
  ::当理性表达式分母的分母因子不从分子中取消一个因子时,会发生垂直的单点。当您有一个因子不取消时,与其在 x 值上设置一个洞,倒不如以该x 值设置一个洞,则存在垂直的单点。垂直的单点由虚点垂直线代表。大多数计算器不会识别垂直的单点,而有些计算器会错误地绘制一个陡峭的线作为该正点实际存在的函数的一部分。

  播放段落

  Your job is to be able to identify vertical asymptotes from a function and describe each asymptote using the equation of a vertical line.  
  ::您的工作是能够从一个函数中识别垂直的静态, 并使用垂直线的方程式描述每个静态 。

  播放段落

  Take the following rational function:
  ::采取以下合理功能:

  播放段落

  $\begin{array}{r}f(x)=\frac{(2x-3)(x+1)(x-2)}{(x+2)(x+1)}\end{array}$
  :xx) = (2x-3) (x+1) (x-2) (x+2) (x) (x+1)

  播放段落

  To identify the holes and the equations of the vertical asymptotes, first decide what factors cancel out. The factor that cancels represents the removable discontinuity.  There is a hole at (-1, 15).  The vertical asymptote occurs at $\begin{array}{r}x=-2\end{array}$  because the factor $\begin{array}{r}x+2\end{array}$  does not cancel. 
  ::要识别垂直静态的洞和方程式, 请先决定取消的因素。 取消的因素代表可移动的不连续性。 在 (-1, 15) 上有一个洞。 垂直的静态出现在 x2 上, 因为因子 x+2 不取消 。

  播放段落

  Watch the following video, focusing on the parts about vertical asymptotes.
  ::关注下一段影片, 关注垂直微粒的部位。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked how asymptotes are different than holes. Holes occur when factors from the numerator and the denominator cancel.  When a factor in the denominator does not cancel, it produces a vertical asymptote.  Both holes and vertical asymptotes restrict the domain of a rational function. 
  ::早些时候,有人问您小数点与洞有什么不同。 当分子和分母中的因素取消时, 空洞就会出现。 当分母中的一个因素不取消时, 它会产生垂直小数点。 洞和垂直小数点都会限制一个理性函数的域 。

  播放段落

  Example 2
  ::例2

  播放段落

  Write a function that fits the following criteria:
  ::写入符合以下标准的函数 :

  播放段落
  • Vertical asymptotes at 0 and 3
    ::0 和 3 0 和 3 的垂直静态
  播放段落
  • Zeroes at 2 and 5
    ::2和5时为零
  播放段落
  • Hole at (4, 2)
    ::洞口( 4, 2)

  播放段落

  Each criteria helps build the function.  The vertical asymptotes imply that the denominator has two factors that do not cancel with the numerator:
  ::每个标准都有助于构建函数。 垂直静态表示分母有两个不与分子取消的因素 :

  播放段落

  $\begin{array}{r}\frac{1}{x\cdot (x-3)}\end{array}$
  ::1x%(x- 3)

  播放段落

  The zeroes at 2 and 5 imply the numerator has two factors that do not cancel.
  ::2和5的零表示分子有两个不取消的因素。

  播放段落

  $\begin{array}{r}\frac{(x-2)(x-5)}{x\cdot (x-3)}\end{array}$
  :x-2(x-5)(x-5)(x-3)

  播放段落

  The hole at (4, 2) implies that there is a factor $\begin{array}{r}x-4\end{array}$  that cancels on the numerator and the denominator. 
  ::在(4,2)处的洞意味着有一个因数x-4可以取消分子和分母。

  播放段落

  $\begin{array}{r}\frac{(x-2)(x-5)(x-4)}{x\cdot (x-3)(x-4)}\end{array}$
  :x-2)(x-5)(x-4)(x-4)(x-3)(x-4)())

  播放段落

  The tricky part is that the height of the function must be 2 after the $\begin{array}{r}x-4\end{array}$  factor has been canceled and the 4 is substituted in.  Currently it is $\begin{array}{r}-\frac{1}{2}\end{array}$ .
  ::棘手的部分是,在 X-4 系数取消后,函数的高度必须为 2, 而替换为 4。 目前为 -12 。

    $\begin{array}{r}\frac{(4-2)(4-5)}{4\cdot (4-3)}=-\frac{1}{2}\end{array}$

  播放段落

  In order to make the hole exist at a height of 2, you need to multiply the function by a scalar of -4. 
  ::要让洞在高度为2时存在, 您需要将函数乘以 - 4 的弧度 。

  播放段落

  $\begin{array}{r}f(x)=\frac{-4(x-2)(x-5)(x-4)}{x\cdot (x-3)(x-4)}\end{array}$
  :xx)4(x-2)(x-5)(x-4)(x-4)x(x-3)(x-4)x(x-3)(x-4)

  播放段落

  Example 3
  ::例3

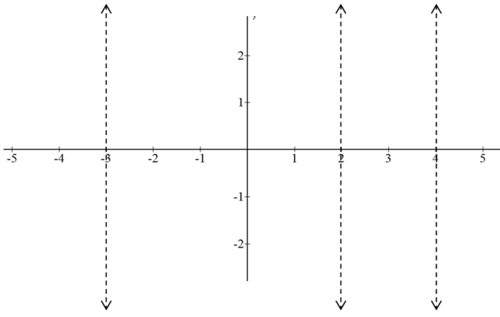
  播放段落

  Draw the vertical asymptotes for the following function. 
  ::为以下函数绘制垂直空位图 。

  播放段落

  $\begin{array}{r}f(x)=\frac{1}{(x-4)(x-2)(x+3)}\end{array}$
  :xx)=1(x-4)(x-2)(x+3)

  

  
  

  播放段落

  Note that you may not know the characteristics of what the function does inside these vertical lines.  You will soon learn how to use sign tests as well as techniques you’ve already learned to fill in the four sections that this function is divided into. 
  ::请注意, 您可能不知道该函数在这些垂直线内做什么的特性 。 您很快会学会如何使用签名测试以及您已经学会的填充此函数分为的四节的技术 。

  播放段落

  Example 4
  ::例4

  播放段落

  Identify the holes and equations of the vertical asymptotes of the following rational function.
  ::识别以下理性函数的垂直空格和方程式的洞和方程。

  播放段落

  $\begin{array}{r}f(x)=\frac{3(x-1)(x+2)(x-3)(x+4)}{5\left(x+\frac{1}{2}\right)(2+x)(3-x)(x-8)}\end{array}$
  :xx) = 3(x- 1)(x+2)(x-3)(x+4)(x+4) 5(x+12)(2+x)(3-x)(x-8)

  播放段落

  The vertical asymptotes occur at $\begin{array}{r}x=-\frac{1}{2},x=8\end{array}$ .  Holes occur when $\begin{array}{r}x\end{array}$  is -2 and 3.  To get the height of the holes at these points, remember to cancel what can be canceled and then substitute the values.  A very common mistake is to forget to cancel $\begin{array}{r}\frac{x-3}{3-x}=-1\end{array}$ . 
  ::x12,x=8. 垂直负位数出现在 x -2 和 3 。 要在这些点达到洞的高度, 请记住取消可以取消的内容, 然后替换值 。 一个非常常见的错误是忘记取消 x - 33 - x1 。

  播放段落

  $$\begin{array}{rl}g(x)& =\frac{-3(x-1)(x+4)}{5\left(x+\frac{1}{2}\right)(x-8)}\\ g(-2)& =\frac{6}{25}\\ g(3)& =\frac{12}{25}\end{array}$$

  
  ::g(xx) 3(x- 1)(x+4)5(x+12)(x-8)g(-2)=625g(3)=1225

  播放段落

  The holes are at $\begin{array}{r}\left(-2,\frac{6}{25}\right),\left(3,\frac{12}{25}\right)\end{array}$ .
  ::洞在(-2,625)处(3,1225)。

  播放段落

  Example 5
  ::例5

  播放段落

  Identify the domain of the following function and then identify the holes and vertical asymptotes. 
  ::识别以下函数的域,然后识别洞和垂直微粒。

  播放段落

  $\begin{array}{r}f(x)=\frac{(3x-4)(1-x)(x^2+4)}{(3x-2)(x-1)}\end{array}$
  :xx) = (3x-4)(1) = (x) = (3x-4)(1) = (x) = (x2+4)(3x-2)(x-1)

  播放段落

  The domain of the function written in interval notation is:  $\begin{array}{r}\left(-\mathrm{\infty },\frac{2}{3}\right)\cup \left(\frac{2}{3},1\right)\cup (1,\mathrm{\infty })\end{array}$ . Note that the domain is all real numbers except for where the denominator is zero. 
  ::以间距符号写入的函数域为 (, 23) (23), (1, ) (1, ) 。 请注意, 域除分母为零的域外, 全部为真实数字 。

  播放段落

  There are two discontinuities: one is a hole and one is a vertical asymptote.  The hole occurs at (1, 5).  The vertical asymptote occurs at $\begin{array}{r}x=\frac{2}{3}\end{array}$ .
  ::有两种不连续性:一个是洞,一个是垂直空洞。洞在(1, 5) 时发生。 垂直空洞在 x=23 时发生。

  播放段落

  Notice that holes are identified as points while vertical asymptotes are identified as lines of the form $\begin{array}{r}x=a\end{array}$  where $\begin{array}{r}a\end{array}$  is some constant .
  ::注意将空洞确定为点,而将垂直微粒点确定为表x=a的线条,其表单是某种常数。

  Summary

  播放段落 Vertical asymptotes occur at values that make the denominator zero. ::使分母为零的值发生垂直负负位数。 播放段落 Vertical asymptotes differ from holes as they occur when a factor of the denominator does not cancel with a factor from the numerator. ::当分母因数不与分子因数取消时,垂直微量与孔的大小不同。 播放段落 Vertical asymptotes are represented by a dotted vertical line. ::垂直空位由虚形垂直线表示。

  播放段落

  Review
  ::回顾

  播放段落

  1.  Write a function that fits the following criteria:
  ::1. 撰写符合下列标准的函数:

  播放段落
  • Vertical asymptotes at 1 and 4
    ::1 和 4 1 和 1 和 4 的垂直空位数
  播放段落
  • Zeroes at 3 and 5
    ::3和5时为零
  播放段落
  • Hole at (6, 3)
    ::洞口(6,3)

  播放段落

  2.  Write a function that fits the following criteria:
  ::2. 撰写符合下列标准的函数:

  播放段落
  • Vertical asymptotes at -2 and 2
    ::-2 和 2 的垂直空位数
  播放段落
  • Zeroes at 1 and 5
    ::1和5时为零
  播放段落
  • Hole at (3, -4)
    ::洞口( 3, 4)

  播放段落

  3.  Write a function that fits the following criteria:
  ::3. 撰写符合以下标准的功能:

  播放段落
  • Vertical asymptotes at 0 and 3
    ::0 和 3 0 和 3 的垂直静态
  播放段落
  • Zeroes at 1 and 2
    ::1和2时为零
  播放段落
  • Hole at (8, 21)
    ::洞口( 8, 21)

  播放段落

  4.  Write a function that fits the following criteria:
  ::4. 撰写符合下列标准的函数:

  播放段落
  • Vertical asymptotes at 2 and 6
    ::2 和 6 2 和 6 的垂直空数
  播放段落
  • Zero at 5
    ::5时零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零
  播放段落
  • Hole at (4, 1)
    :4, 1) 洞口(4, 1)

  播放段落

  5.  Write a function that fits the following criteria:
  ::5. 撰写符合以下标准的函数:

  播放段落
  • Vertical asymptote at 4
    ::4 时垂直为空
  播放段落
  • Zeroes at 0 and 3
    ::0和3时为零零
  播放段落
  • Hole at (5, 10)
    ::洞口( 5, 10)

  播放段落

  Give the equations of the vertical asymptotes for the following functions. 
  ::为以下函数给出垂直小数方程式的方程式。

  播放段落

  6.  $\begin{array}{r}f(x)=\frac{(2-x)}{(x-2)(x-4)}\end{array}$
  ::6. f(x) = (2-x)(x-2)(x-4)

  播放段落

  7.  $\begin{array}{r}g(x)=\frac{-x}{(x+1)(x-3)}\end{array}$
  ::7. g(x)xxxx(x+1)(x-3)

  播放段落

  8.  $\begin{array}{r}h(x)=6-\frac{x+2}{(x+1)(x-5)}\end{array}$
  ::8. h(x)=6-x+2(x+1)(x-5)

  播放段落

  9.  $\begin{array}{r}j(x)=\frac{10}{x-3}-\frac{x}{(x+2)(x-3)}\end{array}$
  ::9. j(x)=10x-3-x(x+2)(x-3)

  播放段落

  10.  $\begin{array}{r}k(x)=2-\frac{(4-x)}{(x+3)(x-4)}\end{array}$
  ::10. k(x)=2-(4-x)(x+3)(x-4)

  播放段落

  Identify the holes and equations of the vertical asymptotes of the following rational functions.
  ::识别以下理性函数的垂直空格和方程式的洞和方程。

  播放段落

  11. $\begin{array}{r}f(x)=\frac{3(x-1)(x+1)(x-4)(x+4)}{4(x+4)(2+x)(4-x)(x+1)}\end{array}$
  ::11. f(x)=3(x-1)(x+1)(x-4)(x+4)(x+4)4(x+4)(2+4)(2)+4(4)-x(x+1)

  播放段落

  12. $\begin{array}{r}g(x)=\frac{x(x-3)(x-8)(x-3)(x+4)}{7(x+1)(1+x)(3-x)(x-8)}\end{array}$
  ::12. g(x)=xx(x-3)(x-8)(x-3)(x+4)7(x+1)(1)+x(3)-x(x-8)

  播放段落

  State the domain of the following rational functions.
  ::国家拥有下列合理职能的领域。

  播放段落

  13. $\begin{array}{r}h(x)=\frac{x(x+1)(x-3)(x+4)}{x(3-x)(x-1)}\end{array}$
  ::13. h(x)=x(x+1)(x-3)(x+4)x(3-x)(x-1)

  播放段落

  14. $\begin{array}{r}j(x)=\frac{x^2+3x-4}{x^2-6x-16}\end{array}$
  ::14. j(x) =x2+3x-4x2-6x-16

  播放段落

  15. $\begin{array}{r}k(x)=\frac{2x-10}{x^3+4x^2+3x}\end{array}$
  ::15. kk(x)=2x- 10x3+4x2+3x

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。