5.8 反向三角函数图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 反向三角函数图

  Collapse Expand

  反向三角函数图

  播放段落

  In order for inverses of functions to be functions, the original function must pass the horizontal line test .  Though none of the trigonometric functions pass the horizontal line test, you can restrict their domains so that they can pass.  Then the inverses are produced just like with normal functions.  Once you have the basic , the normal transformation rules apply. 
  ::函数的反函数要成为函数, 原始函数必须通过水平线测试。 虽然三角函数没有一个通过水平线测试, 但您可以限制它们的域, 以便它们能够通过。 然后, 反函数会和正常函数一样产生。 一旦您具备了基本函数, 通常的转换规则就会适用 。

  播放段落

  Why is $\begin{array}{r}{\sin }^{-1}(\sin {370}^{\circ })\ne {370}^{\circ }\end{array}$ ?  Don’t the arcsin and just cancel out? 
  ::为什么是罪孽1370370370?

  播放段落

  Graphs of Inverse Trigonometric Functions
  ::反向三角函数图

  播放段落

  Since none of the six trigonometric functions pass the horizontal line test, you must restrict their domains before finding inverses of these functions.  This is just like the way $\begin{array}{r}y=\sqrt{x}\end{array}$  is the inverse of $\begin{array}{r}y=x^2\end{array}$  when you restrict the domain to $\begin{array}{r}x\ge 0\end{array}$ .
  ::由于六个三角函数都没有通过水平线测试, 在找到这些函数的反面之前, 您必须限制它们的域 。 这就像 y=x 是 y=x2 的反面 。 当您将域限制为 x=0 时, 这就像 y=x 是 y=x2 的反面 。

  播放段落

  Consider the sine graph:
  ::考虑正弦图 :

  

  播放段落

  As a general rule, the restrictions to the domain are either the interval $\begin{array}{r}\left[-\frac{\pi }{2},\frac{\pi }{2}\right]\end{array}$  or $\begin{array}{r}[0,\pi ]\end{array}$  to keep things simple.  In this case sine is restricted to $\begin{array}{r}\left[-\frac{\pi }{2},\frac{\pi }{2}\right]\end{array}$ , as shown above.  To find the inverse, reflect the bold portion across the line $\begin{array}{r}y=x\end{array}$ . The blue curve below shows $\begin{array}{r}f(x)={\sin }^{-1}x\end{array}$ .
  ::作为一般规则,对域的限制要么是简单事物的间隔[2,%2],要么是简单事物的间隔[2,%2]。在此情况下,正弦仅限于[2,%2],如上所示。要找到反方向,请反映横跨y=x线的粗体部分。下面的蓝色曲线显示 f(x)=sin-1,%x。

  

  播放段落

  The result of this inversion is that arcsine will only ever produce angles between $\begin{array}{r}-\frac{\pi }{2}\end{array}$  and $\begin{array}{r}\frac{\pi }{2}\end{array}$ .
  ::这种反向的结果是 弧氰化物只会产生 2和2之间的角。

  播放段落

  The blue curve below shows  $\begin{array}{r}f(x)={\cos }^{-1}x\end{array}$ ?
  ::下面的蓝色曲线显示 f( x) =cos - 1 x?

  

  播放段落

  The portion of cosine that fits the horizontal line test is the interval $\begin{array}{r}[0,\pi ]\end{array}$ . To find the inverse, that portion is reflected across the line $\begin{array}{r}y=x\end{array}$ .
  ::符合水平线测试的余弦部分是间距 [0, ] 。要找到反向,该部分会反射到横线 y=x 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked why sine and arcsine don't always just cancel out. Since arcsine only produces angles between $\begin{array}{r}-\frac{\pi }{2}\end{array}$  and $\begin{array}{r}\frac{\pi }{2}\end{array}$  or $\begin{array}{r}-{90}^{\circ }\end{array}$  to $\begin{array}{r}+{90}^{\circ }\end{array}$  the result of $\begin{array}{r}{\sin }^{-1}(\sin {370}^{\circ })\end{array}$  is $\begin{array}{r}{10}^{\circ }\end{array}$  which is coterminal to $\begin{array}{r}{370}^{\circ }\end{array}$ . 
  ::早些时候,有人问您为什么正弦和弧子不总是取消。 因为弧子只产生 2 和 2 或 – 90 至 +90 之间的角度, 罪1 和 (sin370 ) 的结果是 10 和 370 。

  播放段落

  Example 2
  ::例2

  播放段落

  Graph the function $\begin{array}{r}f(x)=2{\cos }^{-1}(x-1)\end{array}$ .
  ::函数 f( x) = 2cos- 1\\\ (x- 1) 的图形 。

  播放段落

  Since  $\begin{array}{r}f(x)={\cos }^{-1}x\end{array}$  was graphed earlier, now you just need to shift it right one unit and stretch it vertically by a factor of 2.  It intersected the  $\begin{array}{r}x\end{array}$ axis at 1 before and now it will intersect at 2.  It reached a height of $\begin{array}{r}\pi \end{array}$  before and now it will reach a height of $\begin{array}{r}2\pi \end{array}$ .
  ::由于f(x) = cos-1x 先前的图表显示, 现在你只需要将它向右移动一个单位, 并垂直伸展为 2。 它在之前的 1 点交叉 x 轴, 现在它将在2 点交叉。 它在之前达到 高度, 现在将达到 2 点的高度。

  

  播放段落

  Example 3
  ::例3

  播放段落

  Evaluate the following expression with and without a calculator using right triangles and your knowledge of inverse trigonometric functions.
  ::使用右三角形和您对反三角函数的知识,用计算器和不使用计算器来评价以下表达式。

  播放段落

  $\begin{array}{r}\cot \left({\csc }^{-1}\left(-\frac{13}{5}\right)\right)\end{array}$
  :csc-1(-135))

  播放段落

  In order to be able to effectively calculate this out it is best to write the expression explicitly only in terms of functions that your calculator does have. Be aware that some calculators have both  $\begin{array}{r}{\sin }^{-1}x\end{array}$  and  $\begin{array}{r}(\sin x{)}^{-1}.\end{array}$
  ::为了能够有效地计算出这一点, 最好只用计算器的函数来写清楚表达方式。 请注意, 某些计算器既有罪-1x,也有( sinx)-1 。

  播放段落

  The hardest part of this question is seeing the csc as a function (which produces an angle) on a ratio of a hypotenuse of 13 and an opposite side of -5.  The sine of the inverse ratio must produce the same angle, so you can substitute it.
  ::这个问题最棘手的部分是将csc视为一个函数(产生一个角度),其比值为13, 与- 5的相反。 反比的必然值必须产生相同的角度, 以便您可以替代它 。

  播放段落
  • $\begin{array}{r}{\csc }^{-1}\left(-\frac{13}{5}\right)={\sin }^{-1}\left(-\frac{5}{13}\right)\end{array}$
    ::csc-1(-135)=sin-1(-513)
  播放段落
  • $\begin{array}{r}\cot (\theta )=\frac{1}{\tan \theta }\end{array}$
    :)=1tan

  播放段落

  $\begin{array}{r}\cot \left({\csc }^{-1}\left(-\frac{13}{5}\right)\right)=\frac{1}{\tan \left({\sin }^{-1}\left(-\frac{5}{13}\right)\right)}=-\frac{12}{5}\end{array}$
  :csc-1(-135))=1tan(sin-1(-513))=125

  播放段落

  Start with your knowledge that $\begin{array}{r}{\csc }^{-1}\left(-\frac{13}{5}\right)\end{array}$  describes an angle in the third or the fourth quadrant because those are the two quadrants where cosecant is negative.  Since $\begin{array}{r}{\csc }^{-1}\theta \end{array}$  has range $\begin{array}{r}-\frac{\pi }{2},\frac{\pi }{2}\end{array}$ , it only produces angles in quadrant I or quadrant IV.  This triangle must then be in the fourth quadrant.  All you need to do is draw the triangle and identify the cotangent ratio.
  ::首先,您知道 csc- 1 (- 135) 描述第三个或第四个象限的角, 因为这两个象限是阴性的。 由于 csc- 1 范围为 2, 2, 2, 它只产生 I 象限或 四 象限角。 此三角形必须位于第四个象限 。 您需要做的就是绘制三角形, 并识别余切比 。

  

  播放段落

  Cotangent is adjacent over opposite.
  ::共切物就在对面附近

  播放段落

  $\begin{array}{r}\cot \left({\csc }^{-1}\left(-\frac{13}{5}\right)\right)=-\frac{12}{5}\end{array}$
  :csc-1(-135)) 125

  播放段落

  Example 4
  ::例4

  播放段落

  What is the graph of $\begin{array}{r}y={\tan }^{-1}x\end{array}$ ?
  ::您的图是什么 y=tan - 1x ?

  播放段落

  Graph the portion of tangent that fits the horizontal line test and reflect across the line $\begin{array}{r}y=x\end{array}$ .  Note that the graph of arctan is in blue.
  ::绘制符合水平线测试并反射到横线 y=x 的正切值部分。 请注意, arctan 的图形是蓝色的 。

  

  播放段落

  Example 5
  ::例5

  播放段落

  What is the graph of  $\begin{array}{r}y={\csc }^{-1}x\end{array}$
  ::y=csc- 1\\\\ x 的图形

  播放段落

  Graph the portion of cosecant that fits the horizontal line test and reflect across the line $\begin{array}{r}y=x\end{array}$ .
  ::绘制符合水平线测试并反射到横线 y=x 的 cosecant 部分 。

  

  

  播放段落

  Note that  $\begin{array}{r}f(x)={\csc }^{-1}x\end{array}$ is in blue.
  ::请注意 f( x) = csc- 1 x 蓝色 。

  Summary

  播放段落 Inverse trigonometric functions require the original function to pass the horizontal line test, which can be achieved by restricting their domains. ::逆三角函数要求原始函数通过水平线测试,这可以通过限制其域实现。 播放段落 The sine function is restricted to the interval $\begin{array}{r}[-\frac{\pi }{2},\frac{\pi }{2}]\end{array}$  to pass the horizontal line test. ::正弦函数限于通过水平线测试的间隔[2,2]2]。 播放段落 The inverse sine function, arcsine, will only produce angles between $\begin{array}{r}-\frac{\pi }{2}\end{array}$  and $\begin{array}{r}\frac{\pi }{2}.\end{array}$   ::反正正弦函数, arcsine, 只会产生% 2 和% 2 之间的角 。 播放段落 The cosine function is restricted to the interval $\begin{array}{r}[0,\pi ]\end{array}$  to pass the horizontal line test. ::余弦函数限于通过水平线测试的间距 [0] 。 播放段落 The inverse cosine function, arccosine, will only produce angles between 0 and $\begin{array}{r}\pi \end{array}$   ::逆余弦函数, arccosine, 将只产生 0 到 ° 之间的角 。

  播放段落

  Review
  ::回顾

  播放段落

  1. Graph $\begin{array}{r}f(x)={\cot }^{-1}x\end{array}$ .
  ::1. 图f(x)=cot-1x。

  播放段落

  2. Graph $\begin{array}{r}g(x)={\sec }^{-1}x\end{array}$ .
  ::2. 图g(x)=sec-1x。

  播放段落

  Name each of the following graphs.
  ::列出下图的每一个名称。

  3.

  

  4.

  

  5.

  

  6.

  

  7.

  

  播放段落

  Graph each of the following functions using your knowledge of function transformations.
  ::使用您对函数变换的知识,绘制下列函数的每个函数图。

  播放段落

  8.  $\begin{array}{r}h(x)=3{\sin }^{-1}(x+1)\end{array}$
  ::8. h(x) = 3sin- 1 (x+1)

  播放段落

  9.  $\begin{array}{r}k(x)=2{\sin }^{-1}(x)+\frac{\pi }{2}\end{array}$
  ::9. k(x) = 2sin - 1 (x) 2

  播放段落

  10.  $\begin{array}{r}m(x)=-{\cos }^{-1}(x-2)\end{array}$
  ::10. m(x) cos- 1(x-2)

  播放段落

  11.  $\begin{array}{r}j(x)={\cot }^{-1}(x)+\pi \end{array}$
  ::11. j(x) = Cot-1(x)

  播放段落

  12.  $\begin{array}{r}p(x)=-2{\tan }^{-1}(x-1)\end{array}$
  ::12.p(x)%%2tan-1(x-1)

  播放段落

  13.  $\begin{array}{r}q(x)={\csc }^{-1}(x-2)\end{array}$
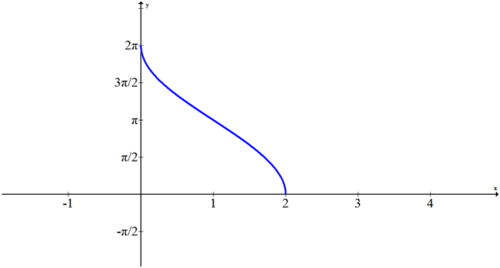
  ::13. q(x) = csc- 1 (x-2)

  播放段落

  14. $\begin{array}{r}r(x)=-{\sec }^{-1}(x)+4\end{array}$
  ::14. r(x)sec-1(x)+4

  播放段落

  15. $\begin{array}{r}t(x)={\csc }^{-1}(x+1)-\frac{3\pi }{2}\end{array}$
  ::15. t (x) = csc- 1 (x+1) - 32

  播放段落

  16. $\begin{array}{r}v(x)=2{\sec }^{-1}(x+2)+\frac{\pi }{2}\end{array}$
  ::16. v(x)=2sec-1(x+2)=2sec-1(x+2)=2

  播放段落

  17. $\begin{array}{r}w(x)=-{\cot }^{-1}(x)-\frac{\pi }{2}\end{array}$
  ::17. w(x)_________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Evaluate each expression.
  ::评估每个表达方式。

  播放段落

  18. $\begin{array}{r}\sec \left({\tan }^{-1}\left[\frac{3}{4}\right]\right)\end{array}$
  ::18 秒( tan-1[ 34])

  播放段落

  19. $\begin{array}{r}\cot \left({\csc }^{-1}\left[\frac{13}{12}\right]\right)\end{array}$
  ::19. ot(csc-1[1312])

  播放段落

  20.  $\begin{array}{r}\csc \left({\tan }^{-1}\left[\frac{4}{3}\right]\right)\end{array}$
  ::20. csc(tan-1[43])

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。