Course: 7.1 矢量的基本特性

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

矢量的基本属性

An airplane being pushed off course by wind and a swimmer’s movement across a moving river are both examples of vectors in action. Points in the coordinate plane describe location. Vectors , on the other hand, have no location and indicate only direction and magnitude . Vectors can describe the strength of forces like gravity or speed and direction of a ship at sea. Vectors are extremely useful in modeling complex situations in the real world.
::飞机被风推离航道和游泳者穿越移动河流的动作都是行进中的矢量的例子。坐标平面上的点描述位置。另一方面,矢量没有位置,只能表示方向和大小。矢量可以像重力、速度和海上船只方向一样描述力量的强度。矢量对于模拟真实世界的复杂情况非常有用。

What are other differences between vectors and points?
::矢量和点之间的其他区别是什么?

Properties of Vectors
::矢量的属性

A two dimensional vector is represented graphically as an arrow with a tail and a head. The head is the arrow and is also called the terminal point. When finding the vector between two points start with the terminal point and subtract the initial point (the tail).
::两维矢量以图形方式表示为箭头,尾巴和头部。头部是箭头,也称为终点。在发现两个点之间的矢量时,从终点开始,减去初始点(尾部)。

The two defining characteristics of a vector are its magnitude and its direction. The magnitude is shown graphically by the length of the arrow and the direction is indicated by the angle that the arrow is pointing. Notice how the following vector is shown multiple times on the same coordinate plane. This emphasizes that the location on the coordinate plane does not matter and is not unique. Each representation of the vector has identical direction and magnitude.
::矢量的两个定义特性是其大小和方向。以箭头的长度以图形方式显示,方向则以箭头指向的角度显示。注意同一坐标平面上如何多次显示下列矢量。这强调坐标平面上的位置并不重要,也不独特。矢量的每个表示都具有相同的方向和大小。

One way to define a vector is as a line segment with a direction. Vectors are said to be equal if they have the same magnitude and the same direction. The absolute value of a vector is the same as the length of the line segment or the magnitude of the vector. Magnitude can be found by using the Pythagorean Theorem or the distance formula.
::定义矢量的一种方式是将矢量定义为带有方向的线条段。如果矢量具有相同的数量和方向,则矢量是相等的。矢量的绝对值与线条段的长度或矢量的大小相同。通过使用 Pythagorean Theorem 或距离公式可以找到磁度。

There are a few different ways to write a vector $\begin{aligned} v \end{aligned}$ .
::以几种不同的方式写一个矢量 v 。

\begin{aligned} v, \vec{v}, \overset{⇀}{v}, or v with a \sim underneath \end{aligned}

::v,v,v,或v 与在下面

When you write about vectors algebraically there are a few ways to describe a specific vector. First, you could describe its magnitude and angle as $\begin{aligned} r, θ \end{aligned}$ . Second, you could describe it as an ordered pair: $\begin{aligned} < x, y > \end{aligned}$ . Notice that when discussing vectors you should use the brackets $\begin{aligned} <> \end{aligned}$ instead of parentheses because it helps avoid confusion between a vector and a point. Vectors can be multidimensional.
::当您写到矢量代数时,有几种方法可以描述特定的矢量。首先,您可以将其大小和角度描述为 r,。第二,您可以把它描述为定购一对:<x,y>。请注意,当讨论矢量时,您应该使用括号 {}而不是括号,因为它有助于避免矢量和点之间的混淆。矢量可以是多维的。

Vectors are often used to describe the movement of objects. To describe the movement of a ship is traveling NNW at 17 knots (nautical mph) as a vector, notice that NNW is halfway between NW and N. When describing ships at sea, it is best to use bearing which has $\begin{aligned} 0^{\circ} \end{aligned}$ as due North and $\begin{aligned} 270^{\circ} \end{aligned}$ as due West. This makes NW equal to $\begin{aligned} 315^{\circ} \end{aligned}$ and NNW equal to $\begin{aligned} {337.5}^{\circ} \end{aligned}$ .
::矢量通常用来描述物体的移动情况。为了将航行在17海里(航空光谱)的船舶的移动情况描述为向量,请注意,向量在向量和向量之间是中点。在描述海上船舶时,最好使用北面0,西面270。这样,向量等于315海里,西北面337.5英寸。

When you see this picture, it turns into a basic trig question to find the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ components of the vector. Note that the reference angle that the vector makes with the negative portion of the $\begin{aligned} x \end{aligned}$ axis is $\begin{aligned} {67.5}^{\circ} \end{aligned}$ .
::当您看到此图片时, 它会变成一个基本三重问题, 以找到矢量的 x 和 Y 组件。请注意, 矢量与 x 轴负部分的引用角是 67.5 \\\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 。

\begin{aligned} \sin {67.5}^{\circ} & = \frac{y}{17}, \cos {67.5}^{\circ} = \frac{x}{17} \\ < x, y > & \approx< - 6.5, 15.7 > \end{aligned}

::67.5y17,cos67.5x17 <x,y6.5.15.7>

Examples
::实例

Example 1
::例1

Earlier, you were asked what the differences between points and vectors are. There are many differences between points and vectors. Points are locations and vectors are made up of distance and angles. Parentheses are used for points and $\begin{aligned} <> \end{aligned}$ are used for vectors. One relationship between vectors and points is that a point plus a vector will yield a new point. It is as if there is a starting place and then a vector tells you where to go from that point. Without the starting point, the vector could start from anywhere.

::早些时候,有人询问了点和矢量之间的差别。点和矢量之间有许多差别。点是位置, 矢量由距离和角度组成。点和矢量使用括号。点和用于点, 矢量使用括号。矢量和点之间的一种关系是, 点加矢量将产生一个新的点。这似乎是一个起始点, 然后是矢量会告诉您从那个点往哪里去。没有起点, 矢量可以从任何地方开始。

Example 2
::例2

Consider the points: $\begin{aligned} A (1, 3), B (- 4, - 6), C (5, - 13) \end{aligned}$ . Find the vectors in component form of $\begin{aligned} \vec{A B}, \vec{B A}, \vec{A C}, \vec{C B} \end{aligned}$ .
::考虑以下各点:A(1,3,3,B(-4,6),C(5)-13). 找出以AB__,BA__,AC__,CB__为组成部分的矢量。

Remember that when finding the vector between two points, start with the terminal point and subtract the initial point.
::记住, 当在两个点之间找到矢量时, 从终点点开始, 并减去初始点。

\begin{aligned} \vec{A B} & =< - 5, - 9 > \\ \vec{B A} & =< 5, 9 > \\ \vec{A C} & =< 4, - 16 > \\ \vec{C B} & =< - 9, 7 > \end{aligned}

::AB5,-9>BA5,-9>BA5,9>BA5,9>AC4,6>CB9,7>

Example 3
::例3

A father is pulling his daughter up a hill. The hill has a $\begin{aligned} 20^{\circ} \end{aligned}$ incline. The daughter is on a sled which sits on the ground and has a rope that the father pulls as he walks. The rope makes a $\begin{aligned} 39^{\circ} \end{aligned}$ angle with the slope. A force diagram is a collection of vectors that each represent a force like gravity or wind acting on an object. Draw a force diagram showing how these forces act on the daughter’s center of gravity:
::父亲将女儿拉上山丘。山上有20英寸的斜坡。女儿在雪橇上,坐在地上,有一条绳子,父亲在走路时拉着绳子。绳子与斜坡角角为39英寸。力图是一个矢量的集合,每个矢量代表着像重力或风一样的力量在物体上行动。绘制一个力图,显示这些力量如何在女儿的重力中心行动 :

a. The force of gravity.
::a. 重力。

b. The force holding the daughter in the sled to the ground.
::b. 将女儿放在雪橇上拖到地上的部队。

c. The force pulling the daughter backwards down the slope.
::c. 将女儿拉向斜坡的部队。

d. The force of the father pulling the daughter up the slope.
::d. 父亲将女儿拉上斜坡时,父亲的力量。

The girl’s center of gravity is represented by the black dot. The force of gravity is the black arrow straight down. The green arrow is gravity’s effect pulling the girl down the slope. The red arrow is gravity’s effect pulling the girl straight into the slope. The blue arrow represents the force that the father is exerting as he pulls the girl up the hill.
::女孩的重心由黑点代表。重力的力量是黑箭直下。绿箭是引力效应,将女孩拉下斜坡。红箭是引力效应,将女孩拉入斜坡。蓝箭代表父亲将女孩拉上山时所施加的力量。

Notice that the father’s force vector (blue) is longer than the force pulling the girl down the hill. This means that over time they will make progress and ascend the hill. Also note that the father is wasting some of his energy lifting rather than just pulling. If he could pull at an angle directly opposing the force pulling the girl down the hill, then he would be using all of his energy efficiently.
::请注意父亲的力量向量(蓝色)比把女孩拉下山的武力(蓝色)要长。这意味着随着时间的流逝,她们将会进步并攀登山丘。还要注意父亲正在浪费他的一些能量,而不是仅仅拉动。如果他能直接从一个角度拉动将女孩拉下山的部队,那么他就会有效地利用他的所有能量。

Example 4
::例4

Center the force diagram from the previous question into the origin and identify the angle between each consecutive force vector.
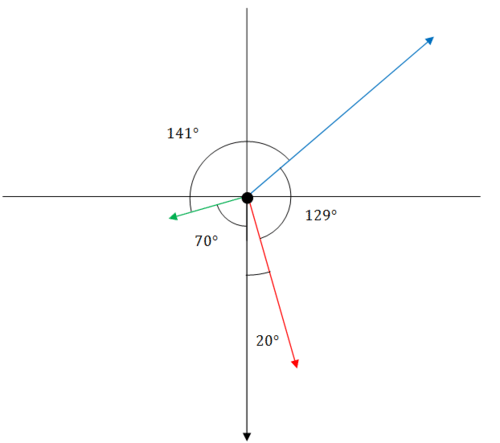
::将上一个问题中的强制图居中到源头,并确定每个连续的强制矢量之间的角。

The $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ axis are included as reference and note that the gravity vector overlaps with the negative $\begin{aligned} y \end{aligned}$ axis. In order to find each angle, you must use your knowledge of supplementary, complementary and vertical angles and all the clues from the question. To check, see if all the angles sum to be $\begin{aligned} 360^{\circ} \end{aligned}$ .
::x 和 y 轴被包含为参考并注意重力矢量与负 y 轴相重叠。要找到每个角度, 您必须使用您对补充、互补和垂直角度以及所有问题线索的知识。要检查, 请检查是否所有角度都等于 360 。

Example 5
::例5

Given the following vectors and point, compute the sum.
::根据以下矢量和点,计算总和。

$\begin{aligned} A = (1, 3), \vec{v} =< 4, 8 >, \vec{u} =< - 1, - 5 > \end{aligned}$
::A=(1,3,3,v4,8>,u1,-5>

$\begin{aligned} A + \vec{v} + \vec{u} = ? \end{aligned}$
::A+vu?

$\begin{aligned} A = (1, 3), \vec{v} =< 4, 8 >, \vec{u} =< - 1, - 5 > . A + \vec{v} + \vec{u} = (4, 6) \end{aligned}$ .
::A=(1,3,5,4,8>,u,1,5>。A+v,4,6。

Summary

Vectors have no location and indicate only direction and magnitude
::矢量没有位置,仅指方向和数量

Vectors can be represented graphically as an arrow with a tail (initial point) and a head (terminal point).
::矢量可以用图形表示为箭头,尾部(初始点)和头部(终点)。

Vectors can be written using magnitude and angle as $\begin{aligned} r, θ, \end{aligned}$ or using an ordered pair as $\begin{aligned} < x, y > . \end{aligned}$
::矢量可以用数值和角度作为 r, , 或用定购的一对作为 <x,y> 来写。

Review
::回顾

1. Describe what a vector is and give a real-life example of something that a vector could model.
::1. 描述矢量是什么,并举例说明矢量可以模拟的东西的真实生活实例。

Consider the points: $\begin{aligned} A (3, 5), B (- 2, - 4), C (1, - 12), D (- 5, 7) \end{aligned}$ . Find the vectors in component form of:
::考虑以下各点:A(3-5),B(-2)-4,C(1,-12),D(-5.7)。

2. $\begin{aligned} \vec{A B} \end{aligned}$
::2. AB_____________________________________________________________________________________________________________________

3. $\begin{aligned} \vec{B A} \end{aligned}$
::3. BA_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4. $\begin{aligned} \vec{A C} \end{aligned}$
::4. AC__________________________________________________________________________________________________________________

5. $\begin{aligned} \vec{C B} \end{aligned}$
::5. CB_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

6. $\begin{aligned} \vec{A D} \end{aligned}$
::6. AD____________________________________________________________________________________________

7. $\begin{aligned} \vec{D A} \end{aligned}$
::7. 达州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州州

8. What is $\begin{aligned} C + \vec{C B} ? \end{aligned}$ Compute this algebraically and describe why the answer makes sense.
::8. C+CB是什么?用这个代数来计算,并描述为什么答案是有道理的。

9. Use your answer to the previous problem to help you determine $\begin{aligned} D + \vec{D A} \end{aligned}$ without doing any algebra.
::9. 使用对上一个问题的回答,帮助您确定 D+DA__,不做代数。

10. A ship is traveling SSW at 13 knots. Describe this ship’s movement in a vector.
::10. 一艘船舶在南南纬13海里处航行,说明该船舶在矢量中的移动情况。

11. A vector that describes a ships movement is $\begin{aligned} < 5 \sqrt{2}, 5 \sqrt{2} > \end{aligned}$ . What direction is the ship traveling in and what is its speed in knots?
::11. 描述船舶移动的矢量为<52,52>,船舶驶向哪个方向,速度如何?

For each of the following vectors, draw the vector on a coordinate plane starting at the origin and find its magnitude.
::对于以下每种矢量,从源头开始,在坐标平面上绘制矢量,并发现其大小。

12. $\begin{aligned} < 3, 7 > \end{aligned}$

13. $\begin{aligned} < - 3, 4 > \end{aligned}$

14. $\begin{aligned} < - 5, 10 > \end{aligned}$

15. $\begin{aligned} < 6, - 8 > \end{aligned}$

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

矢量的基本属性

Properties of Vectors ::矢量的属性

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)