Course: 10.1 极角和矩形坐标

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

极和矩形坐标

In the rectangular coordinate system , points are identified by their distances from the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ axes. In the polar coordinate system, points are identified by their angle on the unit circle and their distance from the origin. You can use basic to translate back and forth between the two representations of the same point. How are lines and other functions affected by this new coordinate system?
::在矩形坐标系统中,点用与 x 和 yax 的距离来识别。在极坐标系统中,点用单位圆的角度和与原点的距离来识别。您可以使用基本的方法来翻译同一点的两个表示之间的反向和反向。线和其他功能如何受这一新的协调系统的影响?

Polar and Rectangular Coordinates
::极和矩形坐标

Rectangular coordinates are the ordinary $\begin{aligned} (x, y) \end{aligned}$ coordinates that you are used to.
::矩形坐标是您使用的普通(x,y)坐标。

represent the same point, but describe the point by its distance from the origin $\begin{aligned} (r) \end{aligned}$ and its angle on the unit circle $\begin{aligned} (θ) \end{aligned}$ . To translate back and forth between polar and rectangular coordinates you should use the basic trig relationships:
::表示同一点,但用其与单位圆的起点( r) 的距离和角度描述点。要在极与矩形坐标之间翻转或翻转, 您应该使用基本三角关系 :

\begin{aligned} \sin θ = \frac{y}{r} \to r \cdot \sin θ = y \\ \cos θ = \frac{x}{r} \to r \cdot \cos θ = x \\ \tan θ = \frac{y}{x} \to θ = {t a n}^{- 1} \frac{y}{x} \end{aligned}

::-1yx

You can also express the relationship between $\begin{aligned} x, y \end{aligned}$ and $\begin{aligned} r \end{aligned}$ using the .
::您也可以使用来表达 x、y 和 r 之间的关系。

$\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$
::x2+y2=r2

Note that coordinates in polar form are not unique. This is because there are an infinite number of that point towards any given $\begin{aligned} (x, y) \end{aligned}$ coordinate.
::请注意,极形坐标并非独一无二。这是因为任何给定(x,y)坐标的点数是无限的。

For example, the point (3, 4) can be written in polar coordinates in at least three different ways. To find $\begin{aligned} θ \end{aligned}$ , use the third equation from above and to find $\begin{aligned} r \end{aligned}$ use the pythagorean theorem.

$\begin{aligned} \tan θ = \frac{4}{3} \\ θ = \tan^{- 1} (\frac{4}{3}) \approx {53.1}^{\circ} \\ r^{2} = 3^{2} + 4^{2} \\ r = 5 \end{aligned}$

::例如, 点( 3, 4) 可以用至少三种不同的方式以极坐标书写。要找到 , 请使用上面的第三个方程, 并找到 r 使用 psytagorean theorem. tan 43\ tan - 1 (43) 53.1\ r2= 32+42r=5

Three equivalent polar coordinates for the point (3, 4) are:
::点(3,4)的三个对等极坐标是:

$\begin{aligned} (5, {53.1}^{\circ}), (5, {413.1}^{\circ}), (- 5, {233.1}^{\circ}) \end{aligned}$

Notice how the third coordinate points in the opposite direction and has a seemingly negative radius. This means go in the opposite direction of the angle.
::注意第三个坐标点的反方向, 并有一个似乎负半径。这意味着向角度的相反方向。

Once you can translate back and forth between points, use the same substitutions to change equations too. A polar equation is written with the radius as a function of the angle. This means an equation in polar form should be written in the form $\begin{aligned} r = \underline{} \end{aligned}$ .
::一旦您可以在点之间翻转或翻转, 也使用相同的替换来更改方程式。以半径作为角度函数来写入极方程式。这意味着极方程式应该以 r 的形式写入。

To write an equation in polar form, use the conversion equations to substitute. For example, to convert $\begin{aligned} y = - x + 1 \end{aligned}$ to polar form make substitutions for $\begin{aligned} y \end{aligned}$ and $\begin{aligned} x \end{aligned}$ . Then, solve for $\begin{aligned} r \end{aligned}$ .
::要写入极形方程式, 请使用转换方程式替换。例如, 要将 yx+1 转换为极形, 将 y. x+1 转换为极形。然后, r 解析 r 。

\begin{aligned} r \cdot \sin θ & = - r \cdot \cos θ + 1 \\ r \cdot \sin θ + r \cdot \cos θ & = 1 \\ r (\sin θ + \cos θ) & = 1 \\ r & = \frac{1}{\sin θ + \cos θ} \end{aligned}

::=1r=1sincoscos1r=1r=1sincos

Examples
::实例

Example 1
::例1

Earlier, you were asked how lines can be represented in the polar coordinate system. The general way to express a line $\begin{aligned} y = m x + b \end{aligned}$ in polar form is $\begin{aligned} r = \frac{b}{\sin θ - m \cdot \cos θ} \end{aligned}$ .
::早些时候, 有人问您在极地坐标系统中如何代表线。以极形式表达 y=mx+b 线的一般方式是 r = bsinmmcos 。

Example 2
::例2

Express the following equation using rectangular coordinates: $\begin{aligned} r = \frac{8}{1 + 2 \cos θ} \end{aligned}$ .
::用矩形坐标表示下列方程式:r=81+2cos。

Use the fact that $\begin{aligned} r = \pm \sqrt{x^{2} + y^{2}} \end{aligned}$ and $\begin{aligned} r \cos θ = x \end{aligned}$ .
::使用 rx2+y2 和 rcosx 。

\begin{aligned} r + 2 r \cdot \cos θ & = 8 \\ \pm \sqrt{x^{2} + y^{2}} + 2 x & = 8 \\ \pm \sqrt{x^{2} + y^{2}} & = 8 - 2 x \\ x^{2} + y^{2} & = 64 - 32 x + 4 x^{2} \\ - 3 x^{2} + 32 x + y^{2} - 64 & = 0 \end{aligned}

::r+2rcos8x2+y2+2+2x=8x2+y2=8_2x2+y2=8_2x2+y2=64=32x4x2+3x2+32x2+32xy2-64=0

This is the equation of a hyperbola.
::这是超重波拉的方程式

Example 3
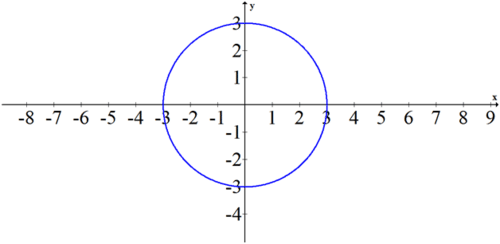
::例3

Sketch the following polar equation: $\begin{aligned} r = 3 \end{aligned}$ .
::绘制以下极方程式: r=3。

Since theta is not in the equation, it can vary freely. This simple equation produces a perfect circle of radius 3 centered at the origin.
::由于 Theta 不在方程中, 它可以自由变化。这个简单方程产生一个完美的半径 3 的圆, 以原点为中心。

You can show this equation is equivalent to $\begin{aligned} x^{2} + y^{2} = 9 \end{aligned}$
::您可以显示此方程式等于 x2+y2=9

Example 4
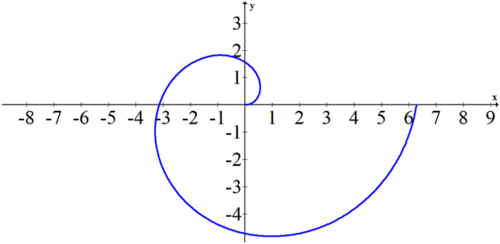
::例4

Sketch the following polar equation: $\begin{aligned} r = θ \end{aligned}$ with $\begin{aligned} θ : 0 \leq θ \leq 2 π \end{aligned}$ .
::绘制以下极性方程: r 和 : 02。

The equation $\begin{aligned} r = θ \end{aligned}$ is an example of a polar equation that cannot be easily expressed in rectangular form . In order to sketch the graph, identify a few key points: $\begin{aligned} (0, 0), (\frac{π}{2}, \frac{π}{2}), (π, π), (\frac{3 π}{2}, \frac{3 π}{2}), (2 π, 2 π) \end{aligned}$ . You should see that the shape is very recognizable as a spiral.
::等式 r 是一个极方程的示例, 无法以矩形形式轻易表达。为了绘制图表, 请指定几个关键点 : (0,0, 0, (2, 2), (), (3, 2, 3), (2) , (2) 。您应该看到, 形状作为螺旋非常可识别。

Example 5
::例5

Translate the following polar expression into rectangular coordinates and then graph.
::将以下极表达式转换为矩形坐标,然后绘制图形。

$\begin{aligned} r = 2 \cdot \sec (θ - \frac{π}{2}) \end{aligned}$
::r=2sec(2)

Simplify the polar equation first before converting to rectangular coordinates.
::在转换成矩形坐标之前先简化极方程。

\begin{aligned} r & = 2 \cdot \sec (θ - \frac{π}{2}) \\ r \cdot \cos (θ - \frac{π}{2}) & = 2 \\ r \cdot \cos (\frac{π}{2} - θ) & = 2 \\ r \cdot \sin θ & = 2 \\ y & = 2 \end{aligned}

::r=22222222222222222222222222222222222222222222

Summary

Polar coordinates represent points on a coordinate plane by describing the distance from the origin $\begin{aligned} (r) \end{aligned}$ and its angle on the unit circle $\begin{aligned} (θ) . \end{aligned}$
::极坐标表示坐标平面上的点,说明出处距离(r)及其单位圆角角()。

To convert between polar and rectangular coordinates use:
- $\begin{aligned} r \cdot \sin θ = y \end{aligned}$
  ::来来来来来来去去去去去去去去去去去去去去去去去去去去去去去去去去
- $\begin{aligned} r \cdot \cos θ = x \end{aligned}$
  ::rcosx
- $\begin{aligned} θ = {t a n}^{- 1} \frac{y}{x} \end{aligned}$
  ::- 1yx
::要在极地和矩形坐标之间转换使用: rsiny rcosx tan-1yx

Review
::回顾

Plot the following polar coordinates.
::绘制以下极坐标。

1. $\begin{aligned} (3, \frac{5 π}{6}) \end{aligned}$

2. $\begin{aligned} (2, \frac{π}{2}) \end{aligned}$

3. $\begin{aligned} (4, - \frac{7 π}{6}) \end{aligned}$

4. $\begin{aligned} (- 2, \frac{5 π}{3}) \end{aligned}$

Give two alternate sets of coordinates for each point.
::每点给两组不同的坐标。

5. $\begin{aligned} (2, 60^{\circ}) \end{aligned}$

6. $\begin{aligned} (5, 330^{\circ}) \end{aligned}$

7. $\begin{aligned} (2, 210^{\circ}) \end{aligned}$

Graph each equation.
::分析每个方程。

8. $\begin{aligned} r = 4 \end{aligned}$
::8 r=4

9. $\begin{aligned} θ = \frac{π}{4} \end{aligned}$ with $\begin{aligned} r \geq 0 \end{aligned}$
::9. 4 和 r0

10. $\begin{aligned} r = 2 θ \end{aligned}$ with $\begin{aligned} θ : 0 \leq θ \leq 2 π \end{aligned}$ .
::10 r = 2 : 0 2 。

Convert each point to rectangular form.
::将每个点转换为矩形形。

11. $\begin{aligned} (4, \frac{2 π}{3}) \end{aligned}$

12. $\begin{aligned} (3, \frac{π}{4}) \end{aligned}$

13. $\begin{aligned} (5, \frac{π}{3}) \end{aligned}$

Convert each point to polar form using radians where $\begin{aligned} 0 \leq θ < 2 π \end{aligned}$ .
::使用 0\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 的弧度将每个点转换为极形。

14. (1, 3)

15. (1, -4)

16. (2, 6)

Convert each equation to polar form.
::将每个方程式转换为极形。

17. $\begin{aligned} x = 3 \end{aligned}$
::17. x=3 17x=3

18. $\begin{aligned} 2 x + 4 y = 2 \end{aligned}$
::18. 2x+4y=2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

极和矩形坐标

Polar and Rectangular Coordinates ::极和矩形坐标

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)