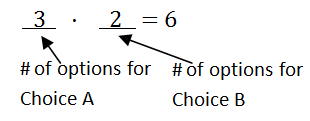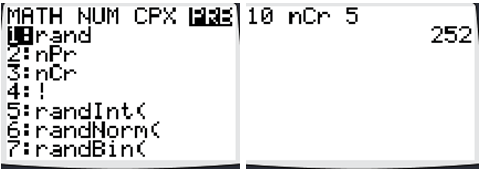Course: 12.6 以变数和组合计数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

以变数和组合计数

Sometimes it makes sense to count the number of ways for an event to occur by looking at each possible outcome . However, when there are a large number of outcomes this method quickly becomes inefficient. If someone asked you how many possible regular license plates there are for the state of California, it would not be feasible to count each and every one. Instead, you would need to use the fact that on the typical California license plate there are four numbers and three letters. Using this information, about how many license plates could there be?
::有时候,通过观察每一种可能的结果来计算事件发生的方式是有道理的。但是,当有大量的结果时,这个方法很快就变得效率低下。如果有人问你加利福尼亚州有多少固定的牌照,那么每个牌照都无法计算。相反,你需要使用一个事实,即典型的加利福尼亚牌照上有四个数字和三个字母。使用这个信息,可以知道有多少牌照?

Counting
::计数

Consider choice $\begin{align*}A\end{align*}$ with three options $\begin{align*}(A_1,A_2,A_3)\end{align*}$ and choice $\begin{align*}B\end{align*}$ with two options $\begin{align*}(B_1,B_2)\end{align*}$ . If you had to choose an option from $\begin{align*}A\end{align*}$ and then an option from $\begin{align*}B\end{align*}$ , the overall total number of options would be $\begin{align*}3 \cdot 2=6\end{align*}$ . The options are $\begin{align*}A_1B_1,A_1B_2,A_2B_1,A_2B_2,A_3B_1,A_3B_2\end{align*}$ .
::考虑选择A有三个选项(A1,A2,A3),选择B有两个选项(B1,B2),如果从A中选择一个选项,然后从B中选择一个选项,选项总数将为32=6。选项总数为A1B1,A1B2,A2B1,A2B2,A3B1,A3B2。

You can see where the six comes from by making a decision chart and using the . First, determine how many decisions you are making. Here, there are only two decisions to make (1: choose an option from $\begin{align*}A\end{align*}$ ; 2: choose an option from $\begin{align*}B\end{align*}$ ), so you will have two “slots” in your decision chart. Next, think about how many possibilities there are for the first choice (in this case there are 3) and how many possibilities there are for the second choice (in this case there are 2). The Fundamental Counting Principle says that you can multiply those numbers together to get the total number of outcomes.
::您可以通过做决定图表和使用 . 首先, 确定您正在做的决定数量。在这里, 只有两个决定需要做出 ( 1 : 从 A 选择一个选项; 2: 从 B 选择一个选项) , 因此您在决定图表中将有两个“ 绘图 ” 。接下来, 考虑第一个选择有多少可能性( 在此情况下有 3 ) , 以及第二个选择有多少可能性( 在此情况下有 2 ) 。基本计数原则指出, 您可以将这些数字相乘, 以获得结果的总数。

Pretend you are going on a road trip with 4 friends in a car that fits 5 people. How many different ways can everyone sit if you have to drive the whole way? A decision chart is a great way of thinking about this problem. You have to sit in the driver’s seat. There are four options for the first passenger seat. Once that person is seated there are three options for the next passenger seat. This goes on until there is one person left with one seat.
::假装与四位朋友一起在一辆适合五人的汽车中旅行。如果必须全程驾驶,每个人可以坐多少种不同的方式? 一张决定图表是一个很好的思考方式。您必须坐在驾驶员的座位上。第一个乘客座位有四个选择。一旦坐在座位上,下一个乘客座位有三种选择。直到有一个人留下一个座位为止。

$\begin{align*}1 \cdot 4 \cdot 3 \cdot 2 \cdot 1=24\end{align*}$

Another type of counting question is when you have a given number of objects, you want to choose some (or all) of them, and you want to know how many ways there are to do this. For example, a teacher has a classroom of 30 students, she wants 5 of them to do a presentation, and she wants to know how many ways this could happen. These types of questions have to do with combinations and permutations. The difference between combinations and permutations has to do with whether or not the order that you are choosing the objects matters.
::计算问题的另一类型是当您有指定数量的对象时, 您想要选择其中的一部分( 或全部) , 您想要知道有多少方法可以这样做。例如, 教师的教室有30名学生, 她想要其中的5名学生做演示, 她想要知道这可以发生的方式。这些类型的问题与组合和变异有关。组合和变异的区别取决于您选择对象的顺序是否重要。

A teacher choosing a group to make a presentation would be a problem, because order does not matter.
::选择一组教师进行演示将是一个问题,因为秩序无关紧要。

A teacher choosing 1 ^st , 2 ^nd , and 3 ^rd place winners in a science fair would be a problem, because the order matters (a student getting 1 ^st place vs. 2 ^nd place are different outcomes).
::在科学博览会中选择第一、第二和第三位优胜者的教师将是一个问题,因为顺序很重要(学生获得第一位与第二位的结果不同)。

Recall that the symbol, !, means to multiply every whole number up to and including that whole number together. For example, $\begin{align*}5!=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\end{align*}$ . The factorial symbol is used in the formulas for permutations and combinations.
::提醒注意此符号, 意思是将每个整数乘以到并包含整数。例如 5! = 5= 54321。该系数符号用于变换和组合的公式中。

Combination Formula: The number of ways to choose $\begin{align*}k\end{align*}$ objects from a group of $\begin{align*}n\end{align*}$ objects is:
::组合公式:从一组 n 对象中选择 k 对象的方法数为 :

$\begin{align*}_nC_k=\dbinom{n}{k}=\frac{n!}{k! \left(n-k\right)!}\end{align*}$
::NCK=(nk)=n.k! (n-k)! (n-k)!

Permutation Formula: The number of ways to choose and arrange $\begin{align*}k\end{align*}$ objects from a group of $\begin{align*}n\end{align*}$ objects is:
::变异公式:选择和排列 n 组对象的 k 对象的方法数为:

$\begin{align*}_nP_k=k!\dbinom{n}{k}=k! \cdot \frac{n!}{k!\left(n-k\right)!}=\frac{n!}{\left(n-k\right)!}\end{align*}$
::NPKK! (nKK) ! (nK) ! (nK) ! (nK) ! (nK) ! (nK) ! (nK) !

Notice that in both permutation and you are not allowed to repeat your choices. Any time you are allowed to repeat and order does not matter, you can use a decision chart. (Problems with repetition where order does not matter are more complex and are not discussed in this text.)
::请注意, 在排列和您不允许重复您的选择。每当您被允许重复和顺序无关紧要时, 您可以使用一个决定图表。 (如果顺序无关紧要, 重复的问题比较复杂, 本文中不讨论。 )

Whenever you are doing a counting problem, the first thing you should decide is if the problem is a decision chart problem, a permutation problem, or a combination problem. You will find that can also be solved with decision charts. The opposite is not true. There are many decision chart problems (ones where you are allowed to repeat choices) that could not be solved with the permutation formula.
::当您在计数时遇到问题时,首先需要决定的问题是决定图表问题、变异问题还是组合问题。您会发现这个问题也可以通过决定图表来解决。相反的情况并非如此。许多决定图表问题(允许重复选择的问题)无法用调整公式解决。

Note: Here you have only begun to explore counting problems. For more information about combinations, permutations, and other types of counting problems, consult a Probability text.
::注意: 这里您只开始探索计数问题。欲了解关于组合、变换和其他类型计数问题的更多信息, 请查阅概率文本。

Examples
::实例

Example 1
::例1

Earlier, you were asked how many California license plates could be created. A license plate that has 3 letters and 4 numbers can be represented by a decision chart with seven spaces. You can use a decision chart because order definitely does matter with license plates. The first spot is a number, the next three spots are letters and the last three spots are numbers. Note that when choosing a license plate, repetition is allowed.
::早些时候,有人问您可以创建多少加利福尼亚州牌照。一个牌照有3个字母和4个号码的牌照可以通过一个带有7个空格的决策图表来代表。您可以使用一个决策图表,因为秩序与牌照确实有关系。第一个空位是数字,接下来的3个空位是字母,最后3个空位是数字。请注意,在选择牌照时,允许重复。

\begin{aligned} 10 \cdot 26 \cdot 26 \cdot 26 \cdot 10 \cdot 10 \cdot 10 = 26^{3} \cdot 10^{4} = 175, 760, 000 \end{aligned}

$\begin{align*}10 \cdot 26 \cdot 26 \cdot 26 \cdot 10 \cdot 10 \cdot 10=26^3 \cdot 10^4=175,760,000\end{align*}$

This number is only approximate because in reality there are certain letter and number combinations that are not allowed, some license plates have extra symbols, and some commercial and government license plates have more numbers, fewer letters or blank spaces.
::这个数字只是近似数字,因为在现实中,某些字母和数字组合是不允许的,有些牌照有额外的符号,有些商业和政府牌照有较多的号码、较少的字母或空白。

Example 2
::例2

How many different ways can the gold, silver and bronze medals be awarded in an Olympic event with 12 athletes competing?
::在有12名运动员参加竞赛的奥林匹克活动中,金、银和铜奖章可以授予多少种不同的方式?

Order does matter with the three medals because the arrangement 1 gets gold, person 2 gets silver, and person 3 gets bronze is different than person 2 gets gold, person 3 gets silver, and person 1 gets bronze. Thus, this is a permutation problem. You will start with 12 athletes and then choose and arrange 3 different winners.
::顺序与三个奖牌关系重大,因为安排1获得金,人2获得银,人3获得铜不同于人2获得金,人3获得银,人1获得铜。因此,这是一个变换问题。你将从12名运动员开始,然后选择和安排3名不同的获胜者。

$\begin{align*}_{12}P_3=\frac{12!}{\left(12-3\right)!}=\frac{12!}{9!}=\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot \ldots}{9 \cdot \ldots}=12 \cdot 11 \cdot 10=1320\end{align*}$
::12P3=12!(12- 3)!=12!9!=1211_ 11_ 10_

Note that you could also use a decision chart to decide how many possibilities are there for gold (12) how many possibilities are there for silver (11 since one already has gold) and how many possibilities are there for bronze (10). You can use a decision chart for any permutation problem.
::请注意,您也可以使用决定图表来决定黄金(12)有多少可能性(12),银(11)有多少可能性(因为已有黄金),铜(10)有多少可能性。您可以使用决定图表来解决任何变换问题。

$\begin{align*}12 \cdot 11 \cdot 10=1320\end{align*}$

Example 3
::例3

You are deciding which awards you are going to display in your room. You have 8 awards, but you only have room to display 4 awards. Right now you are not worrying about how to arrange the awards so the order does not matter. In how many ways could you choose the 4 awards to display?
::您正在决定您要在您的房间里显示哪些奖项。您有 8 个奖项, 但只有 4 个奖项。现在您并不担心如何安排奖项, 这样命令就无关紧要了。您可以通过多少方式选择 4 个奖项来显示 ?

Since order does not matter, this is a combination problem. You start with 8 awards and then choose 4.
::由于顺序无关紧要, 这是一个组合问题。您先从 8 个奖项开始, 然后选择 4 个奖项。

$\begin{align*}_8C_4=\dbinom{8}{4}=\frac{8!}{4!\left(8-4\right)!}=\frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1}=7 \cdot 2 \cdot 5=70\end{align*}$
::8C4=(84)=8!4!(8- 4)!8C4=8C4=8. 4!(8- 4)!8C4=8C4=8C4=8. 4!(8- 4)!8C4=8C4=8C4=8. 4!

Note that if you try to use a decision chart with this question, you will need to do an extra step of reasoning. There are 8 options I could choose first, then 7 left, then 6 and lastly 5.
::请注意, 如果您试图使用一个有关这个问题的决定图表, 您需要做额外的推理步骤。有8种选择我可以先选择, 然后是7, 然后是6, 最后是5 。

$\begin{align*}8 \cdot 7 \cdot 6 \cdot 5=1680\end{align*}$

This number is so big because it takes into account order, which you don’t care about. It is the same result you would get if you used the permutation formula instead of the combination formula. To get the right answer, you need to divide this number by the number of ways 4 objects can be arranged, which is $\begin{align*}4!=24\end{align*}$ . This has to do with the connection between the combination formula and the permutation formula.
::此数字如此大, 因为它会考虑到顺序, 而您并不关心顺序。如果您使用变异公式而不是组合公式, 也会得到同样的结果。要获得正确的答案, 您需要将这个数字除以 4 对象可以排列的方式数, 也就是 4! = 24 。这与组合公式和变异公式之间的联系有关。

Example 4
::例4

There are 20 hockey players on a pro NHL team, two of which are goalies. In how many different ways can 5 skaters and 1 goalie be on the ice at the same time?
::有20个曲棍球运动员在亲NHL球队中,其中两个是守门员。 5个滑冰运动员和1个守门员能同时在冰上以多少种不同的方式出现?

The question asks for how many on the ice, implying that order does not matter. This is combination problem with two combinations. You need to choose 1 goalie out of a possible of 2 and choose 5 skaters out of a possible 18.
::问题在于冰上有多少人, 这意味着顺序无关紧要。这是两种组合的结合问题。您需要从可能的两个组合中选择一个守门员, 然后从可能18个组合中选择5个滑冰员。

$\begin{align*}\dbinom{2}{1}\dbinom{18}{5}=2 \cdot \frac{18!}{5! \cdot 13!}=17136\end{align*}$

Example 5
::例5

How many different 4 digit ATM passwords are there? Assume you can repeat digits.
::有多少不同的 ATM 密码? 假设您可以重复数字。

Order does matter. There are 10 digits and repetition is allowed. You can use a decision chart for each of the four options.
::顺序很重要。有 10 位数, 允许重复。您可以对四个选项中的每一选项使用一个决定图表。

$\begin{align*}10 \cdot 10 \cdot 10 \cdot 10=10,000\end{align*}$

Summary

The Fundamental Counting Principle states that if there are p ways to do one thing and q ways to do another, then there are p \times q ways to do both.
::基本计算原则指出,如果有办法做一件事情,有办法做另一件事情,有办法做两件事情,有办法做两件事情。

Combinations and permutations are used to count the number of ways to choose objects from a group. The order of the objects does not matter with combinations, but does matter with permutations.
::组合和排列用于计算从组合中选择对象的方法数。对象的顺序与组合无关,但与排列有关。

Combination Formula: $\begin{align*}_nC_k = \frac{n!}{k! \left(n-k\right)!}\end{align*}$
::组合公式: nCk=n!k! (n-k)!

Permutation Formula: $\begin{align*}_nP_k = \frac{n!}{\left(n-k\right)!}\end{align*}$
::变异公式: nPk=n! (n-k)!

Review
::回顾

Simplify each of the following expressions so that they do not have a factorial symbol.
::简化下列表达式,使其没有系数符号。

1. $\begin{align*}\frac{7!}{3!}\end{align*}$

2. $\begin{align*}\frac{110!}{105!5!}\end{align*}$

3. $\begin{align*}\frac{52!}{49!}\end{align*}$

4. In how many ways can you choose 3 objects from a set of 9 objects?
::4. 从一组9个对象中选择3个对象的方式有多少?

5. In how many ways can you choose and arrange 4 objects from a set of 15 objects?
::5. 从一组15个天体中选择和安排4个天体的方式有多少?

First, state whether each problem is a permutation/decision chart problem or a combination problem. Then, solve.
::首先,请说明每个问题是一个变异/决定图表问题还是一个组合问题。然后,解决。

6. Suppose you need to choose a new combination for your combination lock. You have to choose 3 numbers, each different and between 0 and 40. How many combinations are there?
::6. 假设您需要为您的组合锁选择一个新的组合组合。您必须选择三个数字, 每个数字不同, 在0到40之间, 有多少组合?

7. You just won a contest where you can choose 2 friends to go with you to a concert. You have five friends who are available and want to go. In how many ways can you choose the friends?
::7. 你刚刚赢得了一场比赛,在那里你可选择两个朋友与你一起参加音乐会,有五个朋友可以参加并想参加音乐会,可以选择多少朋友?

8. You want to construct a 3 digit number from the digits 4, 6, 8, 9. How many possible numbers are there?
::8. 你想用数字4,6,8,9, 建一个3位数的数字吗? 有多少位数?

9. There are 12 workshops at a conference and Sam has to choose 3 to attend. In how many ways can he choose the 3 to attend?
::9. 会议有12个讲习班,Sam必须选择3个参加,他可以选择多少方式选择3个参加?

10. 9 girls and 5 boys are finalists in a contest. In how many ways can 1 ^st , 2 ^nd , and 3 ^rd place winners be chosen?
::10. 9名女孩和5名男孩是一场比赛的决赛选手,以多少方式选出第一、第二和第三位获胜者?

11. For the special at a restaurant you can choose 3 different items from the 10 item menu. How many different combinations of meals could you get?
::11. 对于餐厅的特餐,您可从10项菜单中选择3项不同的菜单。您可以得到多少份不同的膳食组合?

12. You visit 12 colleges and want to apply to 4 of them. In how many ways could you choose the four to apply to?
::12. 你访问了12所大学,希望申请其中4所。你能够以多少方式选择4所大学申请?

13. For the 12 colleges you visited, you want to rank your top five. In how many ways could you rank your top 5?
::13. 在你访问的12所学院中,你想排在前5名的位子上,以多少种方式排在前5名的位子上?

14. Explain why the following problem is not strictly a permutation or combination problem: The local ice cream shop has 12 flavors. You decide to buy 2 scoops in a dish. In how many ways could you do this if you are allowed to get two of the same scoop?
::14. 解释为什么以下问题不是严格意义上的变异或组合问题:当地冰淇淋店有12种口味。您决定在一个盘子里买2个勺子。如果允许您在同一勺子中买两个,您可以用多少种方式这样做?

15. Your graphing calculator has the combination and permutation formulas built in. Push the MATH button and scroll to the right to the PRB list. You should see $\begin{align*}{_nP}_r\end{align*}$ and $\begin{align*}_nC_r\end{align*}$ as options. In order to use these: 1) On your home screen type the value for $\begin{align*}n \end{align*}$ ; 2) Select $\begin{align*}{_nP}_r\end{align*}$ or $\begin{align*}_nC_r\end{align*}$ ; 3) Type the value for $\begin{align*}k\end{align*}$ ( $\begin{align*}r\end{align*}$ on the calculator). Use your calculator to verify that $\begin{align*}{_{10}C}_5=252\end{align*}$ .
::15. 您的图形计算器有组合和排列公式。按下 MATH 按钮并滚动到 PRB 列表右侧。您应该将 nPr 和 nCr 作为选项。为了使用这些选项1) 在您的主屏幕上输入 n 的值;(2) 选择 nPr 或 nCr;(3) 输入 k (在计算器上输入 r) 的值。使用您的计算器来验证 10C5=252 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

以变数和组合计数

Counting ::计数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)