14.2 确定界限的图表
章节大纲
-
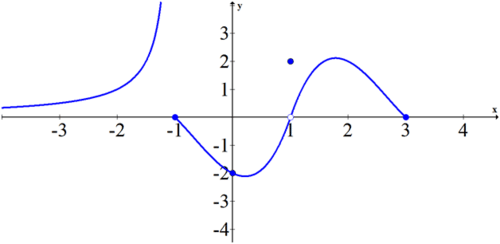
A limit can describe the end behavior of a function. This is called a limit at infinity or negative infinity. A limit can also describe the limit at any normal value. Sometimes this is simply the height of the function at that point. Other times this is what you would expect the height of the function to be at that point even if the height does not exist or is at some other point. In the following graph, what are ?
::限制可以描述函数的结束行为。这被称为无限或负无限的限制。限制也可以以任何正常的 x 值来描述限制。有时,这只是函数在那个点的高度。其他时候,即使高度不存在,或者在其他点,你也会期待函数在那个点的高度。在下图中,什么是 f(3), limx%3f(x), limxf(x)?Using Graphs to Find Limits
::使用图表查找限制When evaluating the limit of a function from its graph, you need to distinguish between the function evaluated at the point and the limit around the point.
::在从一个函数的图形中评价该函数的极限时,需要区分在点上评价的函数和在点周围评价的函数。Functions like the one above with discontinuities, asymptotes and holes require you to have a very solid understanding of how to evaluate and interpret limits.
::类似上述功能的功能,如不连续、无症状和孔,需要您对如何评估和解释限制有非常扎实的了解。At , the function is undefined because there is a vertical asymptote. You would write:
::At x=a, 函数未定义, 因为有一个垂直的空位。 您会写入 :
::f(a) = DNE, limxaf(x) = DNEAt , the function is defined because the filled in circle represents that it is the height of the function. This appears to be at about 1. However, since the two sides do not agree, the limit does not exist here either.
::在 x=b 点, 函数是定义的, 因为以圆填满的表示是函数的高度。 这似乎是大约为 1 点, 但是由于双方并不同意, 限制在这里也不存在 。
::f(b) = 1, limxbf(x) = DNEAt , the function has a discontinuity in the form of a hole. It is as if the point has been lifted up and placed at . You can evaluate both the function and the limit at this point, however these quantities will not match. When you evaluate the function you have to give the actual height of the function, which is 1 in this case. When you evaluate the limit, you have to give what the height of the function is supposed to be based solely on the neighborhood around 0. By neighborhood around 0, we mean what is happening on the lines around , not the at the point. Since the function appears to reach a height of -2.4 from both the left and the right, the limit does exist.
::在 x= 0 时, 函数以洞的形式具有不连续性。 这就像点( 0, ~ 2. 4) 已被提升并放置在 0, 1 上。 您可以在此点对函数和限制进行评估, 但是这些数量将不匹配。 当您评估函数的实际高度时, 您必须给定函数的实际高度, 在本案中为 1 。 当您对限制进行评估时, 您必须给给给定函数的高度应该仅以 0 左右的邻里为基础。 大约 0 时, 我们指 x= 0 左右行发生的情况, 而不是点发生的情况。 由于函数似乎从左侧和右侧达到 - 2.4 高度, 限制就存在了 。
::f( 0) = 1, limx% 0f( x) 2.4At , the limit does not exist because the left and right hand neighborhoods do not agree on a height. On the other hand, the filled in circle represents that the function is defined at to be -3.
::在 x= c 时, 限制并不存在, 因为左侧和右手邻里在高度上无法达成一致 。 另一方面, 以圆填充表示函数在 x= c 下定义为 - 3 。
::f(c) 3, limx}cf(x) = DNEAt you may only discuss the limit of the function since it is not appropriate to evaluate a function at infinity (you cannot find ). Since the function appears to increase without bound, the limit does not exist.
::在 x 键上,您只能讨论该函数的限度, 因为不适宜在无限范围内评价函数( 您找不到 f () ) 。 由于该函数似乎无约束地增加, 该限制并不存在 。
::limxf(x) = DNEAt the graph appears to flatten as it moves to the left. There is a horizontal asymptote at that this function approaches as .
::x+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
::limxf(x)=0When evaluating limits graphically, your main goal is to determine whether the limit exists. The limit only exists when the left and right sides of the functions meet at a specific height. Whatever the function is doing at that point does not matter for the sake of limits. The function could be defined at that point, could be undefined at that point, or the point could be defined at some other height. Regardless of what is happening at that point, when you evaluate limits graphically, you only look at the neighborhood to the left and right of the function at the point.
::当图形化地评价限制时,您的主要目标是确定限制是否存在。只有当函数的左侧和右侧在特定高度相交时,限制才存在。无论该函数此时做什么都无关紧要。当此点可以定义该函数时,可以在该点上未定义,或者该点可以在其他高度上定义。无论该点发生什么,当您用图形化地评估限制时,您只能查看该点函数的左侧和右侧。Examples
::实例Example 1
::例1Earlier, you were asked to find given the graph of the function to be:
::早些时候, 您被要求查找 f(3), limx}3f( x), limx}}f( x) , 给出函数 f( x) 的图表 :
::limx%3f(x)=12
::f(3)=3
::limxf(x) = DNEExample 2
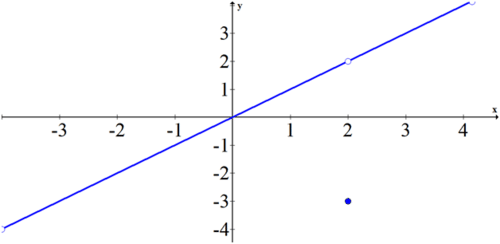
::例2Evaluate the following expressions using the graph of the function .
::使用函数 f(x) 的图形评价以下表达式。-
::limxf(x) -
::limx1f( x) -
::limx0f(x) -
::limx1f(x) -
::limx%3f(x) -
:f-1-1)
-
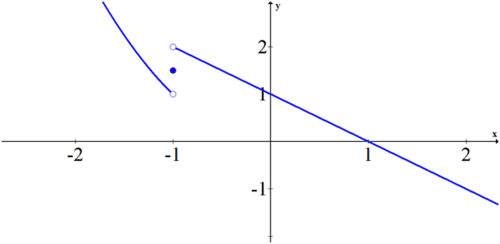
::f(2) f(2) -
::f(1) f(1) -
::f(3) f(3)
-
::limxf(x)=0 -
::limx1f(x) = DNE -
::立方厘米#0f( x) @%%2 -
::limx% 1f( x) =0 -
(This is because only one side exists and a regular limit requires both left and right sides to agree)
::limx}3f(x) = DNE (这是因为只有一方存在,而常规限制要求左和右双方同意) -
::f( - 1) =0 -
:f0)%2
-
::f(1)=2 -
::f(3)=0
Example 3
::例3Sketch a graph that has a limit at , but that limit does not match the height of the function.
::绘制一个在 x=2 上有限制的图形,但该限制与函数的高度不符。While there are an infinite number of graphs that fit this criteria, you should make sure your graph has a removable discontinuity at .
::虽然有无数符合此标准的图表,但您应该确保您的图表在 x=2 时具有可移动的不连续性。Example 4
::例4Sketch a graph that is defined at but does not exist.
::绘制一个在 x1 上定义的图, 但是 limx1f(x) 不存在 。The graph must have either a jump or an infinite discontinuity at and also have a solid hole filled in somewhere on that vertical line.
::图形在 x1 时必须有一个跳跃或无限不连续性, 并在垂直线的某个地方填满一个坚固的洞。Example 5
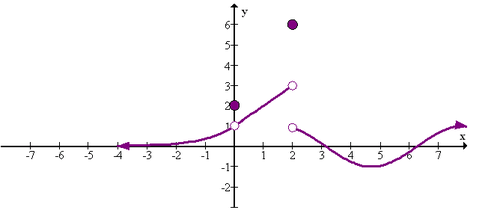
::例5Evaluate and explain how to find the limits as approaches 0 and 1 for the graph below:
::评估并解释下图如何找到 xroaches 0 和 1 的极限值:
::limx% 0f( x) = 2, limx% 1f( x) =1Both of these limits exist because the left hand and right hand neighborhoods of these points seem to approach the same height. In the case of the point the function happened to be defined there. In the case of the point the function happened to be defined elsewhere, but that does not matter. You only need to consider what the function does right around the point.
::这两个限制都存在,因为左手和右手周围的点似乎接近相同的高度。在点( 0, 2) 的情况下,函数恰好在那里被定义。在点(1, 1) 的情况下,函数碰巧在别处被定义,但这并不重要。您只需要考虑函数在点周围的正确作用。Summary -
A limit can describe the end behavior of a function, called a limit at infinity or negative infinity, and can also describe the limit at any normal value.
::限制可以描述一个函数(称为无限或负无限)的最终行为,也可以以任何正常值描述该限制。 -
When evaluating the limit of a function from its graph, distinguish between the function evaluated at the point and the limit around the point.
::在从一个函数的图形中评价该函数的极限时,区分在点上评价的函数和点周围的界限。 -
The limit only exists when the left and right sides of the functions meet at a specific height, regardless of what the function is doing at that point.
::只有当函数的左侧和右侧在特定高度相交时,无论该函数当时正在做什么,限制才存在。
Review
::回顾Use the graph of below to evaluate the expressions in 1-6.
::使用下面f(x)的图形来评价 1-6 中的表达式。1.
::1. limxf(x)2.
::2. limxf(x)3.
::3. limx%2f(x)4.
::4. limx%0f(x)5.
::5.f(0)6.
::6.f(2) 6 f(2)Use the graph of below to evaluate the expressions in 7-13.
::使用下方 g(x) 的图形来评价 7- 13 中的表达式 。7.
::7. limxg(x)8.
::8. limxg(x)9.
::9. limx%2g(x)10.
::10. limx0g(x)11.
::11. 立方4g(x)12.
::12. g(0)13.
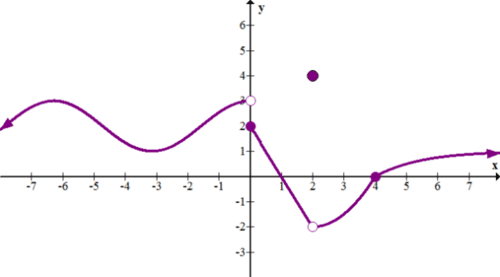
::13.g(2)14. Sketch a function such that , but .
::14. 将函数 h(x) 折叠成 h(2)=4, 但 limx%2h(x) = DNE 。15. Sketch a function such that , but .
::15. 绘制函数j(x),使 j(2) = 4, 但 limx%2j(x) = 3。Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -