Course: 1.5 垂直和水平移动

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

垂直和水平移动

Horizontal and vertical transformations are two of the many ways to convert the basic parent functions in a function family into their more complex counterparts.
::横向和纵向转变是将功能家庭的基本母函数转换为更为复杂的对应功能的多种方式中的两种。

What vertical and/or horizontal shifts must be applied to the parent function $\begin{align*}y=x^2\end{align*}$ to make it match the graph of $\begin{align*}g(x)=(x-3)^2+4?\end{align*}$
::对父函数 y=x2 应用什么垂直和/或水平移动才能使其与 g(x) =(x) = (x) 3) 2+4 的图形匹配?

Function Transformations: Shifts
::函数变换:变换

Have you ever tried to draw a picture of a rabbit, cat, or dog? Unless you are talented, even the most common animals can be a bit of a challenge to draw accurately, or even recognizably. One trick that can help even the most “artistically challenged” to create a clearly recognizable basic sketch is demonstrated in nearly all “learn to draw” courses: start with basic shapes. By starting your sketch with simple circles, ellipses, rectangles, etc., the basic outline of the more complex figure is easily arrived at. Details can be added later as necessary, but the figure is already recognizable for what it is.
::你曾经尝试过画兔子、猫或狗的图画吗?除非你很有才华,否则即使是最常见的动物也可能是准确或甚至可以辨认的难题。几乎在所有的“素描”课程中都展示了能够帮助甚至最“艺术挑战者”创建明确识别的基本草图的伎俩:从基本形状开始。通过以简单的圆形、椭圆、矩形等开始你的素描,比较复杂的图样的基本轮廓可以很容易地得到。细节可以在必要时稍后添加,但数字已经可以识别。

The same trick works when graphing equations. By learning the basic shapes of different types of function graphs, and then adjusting the graphs with different types of transformations, even complex graphs can be sketched rather easily. This lesson will focus on two particular types of transformations: vertical shifts and horizontal shifts.
::当图形化方程式时,同样的把戏也可以用同样的把戏。通过学习不同类型函数图形的基本形状,然后用不同类型的变形调整图形,甚至复杂的图形也可以很容易地绘制。这个课程将侧重于两种特定的变形类型:垂直变形和水平变形。

Vertical Shifts
::垂直垂直移动

We can express the application of vertical shifts this way:
::我们可以这样表达垂直转变的应用:

Formally: For any function $\begin{align*}f(x)\end{align*}$ , the function $\begin{align*}g(x)=f(x)+c\end{align*}$ has a graph that is the same as $\begin{align*}f(x)\end{align*}$ , shifted $\begin{align*}c\end{align*}$ units vertically . If $\begin{align*}c\end{align*}$ is positive, the graph is shifted up. If $\begin{align*}c\end{align*}$ is negative, the graph is shifted down.
::形式 : 对于任何函数 f(x), 函数 g(x)=f(x)+c 的图形与 f(x) 相同, 垂直移动 c 单位。如果 c 是正, 则向上移动。如果 c 是负, 则向下移动。

Informally: Adding a positive number after the $\begin{align*}x\end{align*}$ outside the parenthesis shifts the graph up, adding a negative (or subtracting) shifts the graph down.
::非正式: 在括号外的 x 后添加正数, 将图向上移动, 加上负( 减) 将图向下移动。

Take the graph below:
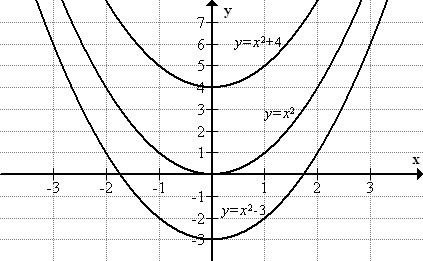
::下图如下:

What must be done to the graph of $\begin{align*}y=x^2\end{align*}$ to convert it into the graphs of $\begin{align*}y=x^2-3\end{align*}$ , and $\begin{align*}y=x^2+4?\end{align*}$
::要将 y=x2 的图形转换成 y=x2-3, 和y=x2+4 的图形, 必须对 y=x2 的图形做些什么 ?

At first glance, it may seem that the graphs have different widths. For example, it might look as if $\begin{align*}y=x^2+4,\end{align*}$ the uppermost of the three parabolas, is thinner than the other two parabolas. However, this is not the case. The parabolas are congruent.
::乍一看,图表似乎有不同的宽度。例如,它可能看起来象Y=x2+4,即三个parabolas的上半部,比另外两个parabolas更薄,但情况并非如此。但parapolas是相同的。

If we shifted the graph of $\begin{align*}y=x^2\end{align*}$ up four units, we would have the exact same graph as $\begin{align*}y=x^2+4\end{align*}$ . If we shifted $\begin{align*}y=x^2\end{align*}$ down three units, we would have the graph of $\begin{align*}y=x^2-3\end{align*}$ .
::如果我们移动 y=x2up 4 个单位的图形, 我们就会有相同的 asy=x2+4 。如果我们移动 y=x2 down 3 个单位, 我们就会有 y=x2 - 3 个单位的图形。

Horizontal Shifts
::水平移动

We can express the application of horizontal shifts this way:
::我们可以这样表达横向转变的应用:

Formally: given a function $\begin{align*}f(x)\end{align*}$ , and a constant $\begin{align*}a>0\end{align*}$ , the function $\begin{align*}g(x)=f(x-a)\end{align*}$ represents a horizontal shift of $\begin{align*}a\end{align*}$ units to the right from $\begin{align*}f(x)\end{align*}$ . The function $\begin{align*}h(x)=f(x+a)\end{align*}$ represents a horizontal shift of $\begin{align*}a\end{align*}$ units to the left.
::形式 : 给定函数 f( x) 和常数 a>0 , 函数 g( x) = f( x) a 表示单位向右水平的移动。函数 h( x) = f( x) +a) 表示单位向左水平的移动。

Informally: Adding a positive number after the $\begin{align*}x\end{align*}$ inside the parenthesis shifts the graph left (somewhat counter-intuitively), while adding a negative (or subtracting) shifts the graph right.
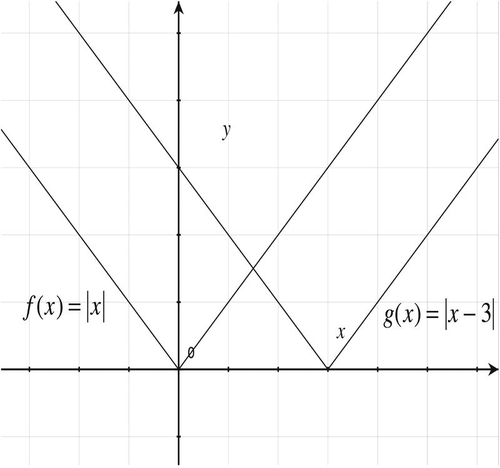
::非正式 : 在括号内的 x 之后添加正数, 使图左移( 某些反直觉) , 而添加负( 减) 将图向右移动。

Apply this knowledge and identify the transformation(s) involved in converting the graph of $\begin{align*}f(x)=|x|\end{align*}$ into $\begin{align*}g(x)=|x-3|\end{align*}$ .
::应用此项知识, 并识别 f( x) x g( x) x- 3 的图形转换过程中所涉及的转换。

From the examples of vertical shifts above, you might think that the graph of $\begin{align*}g(x)\end{align*}$ is the graph of $\begin{align*}f(x)\end{align*}$ shifted 3 units to the left. However, this is not the case. The graph of $\begin{align*}g(x)\end{align*}$ is the graph of $\begin{align*}f(x)\end{align*}$ shifted 3 units to the right.
::从以上垂直移动的例子中,你可能会认为 g(x) 的图形是 f(x) 向左移动 3 个单位的图形。然而,情况并非如此。 g(x) 的图形是 f(x) 向右移动 3 个单位的图形。

The direction of the shift makes sense if we look at specific function values.
::如果我们看看具体的功能值,转变的方向就有意义了。

*$\begin{align}x\end{align}$* ::x x	*$\begin{align}g(x)=\|x-3\|\end{align}$* ::g(x) x- 3
0	3
1	2
2	1
3	0
4	1
5	2
6	3

From the table we can see that the vertex of the graph is the point (3, 0). The function values on either side of $\begin{align*}x=3\end{align*}$ are symmetric and greater than 0.
::从表中可以看出,图形的顶点是点(3,0)。 x=3 的两侧的函数值对称,大于0。

Many times, multiple transformations are applied to the same function. Take the parent function . What transformations must be applied to the parent graph in order to graph
::许多次,多个变换被应用到同一个函数。选择父函数。什么变换必须应用到父图形,以图解

The graph of $\begin{align*}g(x)=(x+2)^2-2\end{align*}$ is the graph of $\begin{align*}y=x^2\end{align*}$ shifted 2 units to the left, and 7 units down.
::g(x) = (x+2) 2-2 的图形是 y=x2 向左移动 2 个单位, 向下移动 7 个单位。

Examples
::实例

Example 1
::例1

Earlier, you were asked what transformations must be applied to $\begin{align*}y=x^2\end{align*}$ in order to graph $\begin{align*}g(x)=(x-3)^2+4\end{align*}$ .
::早些时候,有人询问,要用图g(x)=(x-3)2+4,Y=x2必须应用何种变换。

The graph of $\begin{align*}g(x)=(x-3)^2+4\end{align*}$ is the graph of $\begin{align*}y=x^2\end{align*}$ shifted 3 units to the right, and 4 units up.
::g(x) = (x-3) 2+4 的图形是 y=x2 向右移动 3 个单位, 向上移动 4 个单位。

If you were able to identify the translation congratulations! You are on your way to an excellent conceptual base for manipulating functions.
::如果您能够确认翻译的祝贺! 您正在前往一个极好的概念基础用于操控功能。

Example 2
::例2

Use the graph of $\begin{align*}y=x^2\end{align*}$ to graph the function $\begin{align*}y=x^2-5\end{align*}$ .
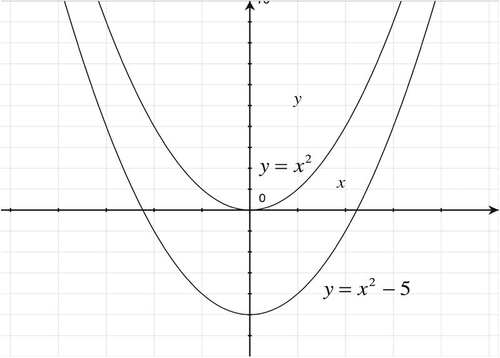
::使用 y=x2 的图形来绘制函数y=x2- 5 的图形。

The graph of $\begin{align*}y=x^2\end{align*}$ is a parabola with vertex at (0, 0).
::y=x2 的图形是一个有顶点为 0, 0 的抛物线。

The graph of $\begin{align*}y=x^2-5\end{align*}$ is therefore a parabola with vertex (0, -5).
::因此,y=x2-5的图形是带有顶点(0,-5)的抛物线。

To quickly sketch $\begin{align*}y=x^2-5\end{align*}$ , you can sketch several points on $\begin{align*}y=x^2\end{align*}$ , and then shift them down 5 units.
::要快速绘制 y=x2 - 5, 您可以在 y=x2 上绘制几个点, 然后将其向下移动 5 个单位。

Example 3
::例3

What is the relationship between $\begin{align*}f(x)=x^2\end{align*}$ and $\begin{align*}g(x)=(x-2)^2\end{align*}$ ?
::f(x) =x2andg(x) =(x) =(x) 2 2 之间的关系是什么?

The graph of $\begin{align*}g(x)\end{align*}$ is the graph of $\begin{align*}f(x)\end{align*}$ , shifted 2 units to the right.
::g(x) 的图形是 f(x) 的图形, 将 2 个单位移到右边。

Example 4
::例4

What is the relationship between $\begin{align*}f(x)=x^2-6\end{align*}$ and $\begin{align*}f(x)=x^2\end{align*}$ ?
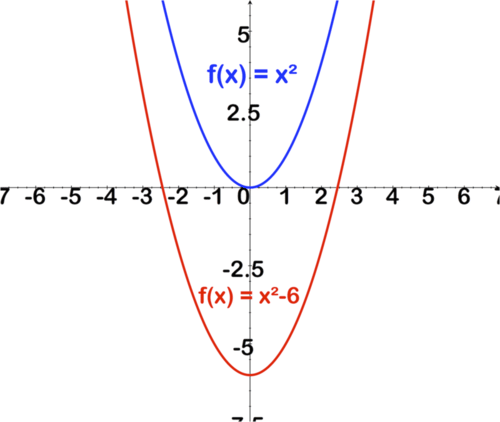
::f( x) =x2- 6和f( x) =x2 之间的关系是什么?

Adding or subtracting a value outside the parenthesis results in a vertical shift.
::在括号外添加或减去一个值会导致垂直变化。

Therefore, the graph of $\begin{align*}f(x)=x^2-6\end{align*}$ is the same as $\begin{align*}f(x)=x^2\end{align*}$ shifted 6 units down.
::因此,f(x)=x2-6的图形与f(x)=x2向下移动6个单位相同。

Example 5
::例5

Use the parent function $\begin{align*}f(x)=|x|\end{align*}$ to graph $\begin{align*}f(x)=|x-4|.\end{align*}$
::使用父函数 f( x)\\\\\ x\\ to graphf( x)\\\\ x- 4\\\ 。

The graph of the absolute value function family parent function $\begin{align*}f(x)=|x|\end{align*}$ is a large “V” with the vertex at the origin.
::绝对值函数的家庭父函数 f( x) 是一个大的“ V ” , 其源头是顶点。

Adding or subtracting inside the parenthesis results in horizontal movement.
::括号内添加或减去导致水平移动。

Recall that the horizontal shift is right for negative numbers and left for positive numbers.
::回顾横向变化对负数和正数都是正确的,而左转则对正数。

Therefore $\begin{align*}f(x)=|x-4|\end{align*}$ is a large “V” with the vertex 4 units to the right of the origin.
::因此,f(x)x-4是一个大的“V”,其顶点4单位与原产地右。

Review
::回顾

Graph the function $\begin{align*}f(x)=2|x-1|-3\end{align*}$ without a calculator.
::函数 f( x) = 2\\\\\\\\\\\\\\\\\\\\\\\3没有计算器的图形。

What is the vertex of the graph and how do you know?
::图形的顶点是什么? 你怎么知道的?

Does it open up or down and how do you know?
::开着还是下着呢? 你怎么知道的?

Given the function $\begin{align*}f(x)=|x|+c,\end{align*}$ if $\begin{align*}c\end{align*}$ is positive, the graph shifts in what direction?
::鉴于函数 f(x) c, 如果 c 是正, 图形会向哪个方向移动 ?

Given the function $\begin{align*}f(x)=|x|+c,\end{align*}$ if $\begin{align*}c\end{align*}$ is negative, the graph shifts in what direction?
::鉴于函数 f(x) c, 如果 c 为负, 图形会向哪个方向移动 ?

Does the function $\begin{align*}g(x)=|x-a|\end{align*}$ represent a shift to the right or the left of the parent function?
::函数 g (x)\\\\\\\\\ a\\\\\\\\\\\\\\\\\\\\\\\\\\\ x( x)\\\\\\\\\\\\\\\\\\\\\\\\\\在父函数向右或向左的转移吗? \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\在父函数向右或向右或向左的函数向右或向左移动?

Does the function $\begin{align*}h(x)=|x+a|\end{align*}$ represent a shift to the right or the left of the parent function?
::函数 h( x)\\\\\ x+a是否代表父函数向右或左的移动 ?

If a graph is in the form $\begin{align*}a \cdot f(x)\end{align*}$ . What is the effect of changing the value of $\begin{align*}a\end{align*}$ ?
::如果图形以 af(x) 的形式出现。改变一个数值的效果是什么?

For #9-10, describe the transformation that has taken place from the parent function $\begin{align*}f(x)=|x|\end{align*}$ .
::对于# 9- 10, 请描述父函数 f( x) 从父函数 f( x) 中发生的变换。

$\begin{align*}f(x)=|x|-5\end{align*}$
::f(xx) x* 5

$\begin{align*}f(x)=5|x+7|\end{align*}$
:xx)=5x+7

For #11-13, write an equation that reflects the transformation applied to the parent function $\begin{align*}g(x)=\frac{1}{x}\end{align*}$ , for it to move in the indicated way.
::对于# 11- 13, 写一个方程式, 反映对父函数 g( x) = 1x 应用的转换, 以便以指示方式移动。

Move two spaces up
::向上移动两个空格

Move four spaces to the right
::向右移动四个空格

Stretch it by 2 in the $\begin{align*}y\end{align*}$ -direction
::将之伸展在Y方向上,再伸展两下

For #14-16, write an equation for each described transformation.
::#14-16,为每个描述的变换写一个方程。

A V-shape shifted down 4 units.
::一个V型形状向下移动了4个单元。

A V-shape shifted left 6 units
::AV形形向左移动6个单元

A V-shape shifted right 2 units and up 1 unit.
::一个V形状向右移动了2个单元,向上移动了1个单元。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

垂直和水平移动

Function Transformations: Shifts ::函数变换:变换

Vertical Shifts ::垂直垂直移动

Horizontal Shifts ::水平移动

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)