Course: 1.7 函数图: 组合转换

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

函数图: 组合转换

How do the different forms of transformations result in the differences between the basic parent functions we have explored and some of the more complex graphs you may have seen? It has likely occurred to you that these individual transformations are not enough to result in such significant differences. How do we then apply the individual transformations so that the more complex graphs may be understood?
::不同形式的变换如何导致我们所探讨的基本父函数与一些你可能见过的更复杂的图表之间的差异? 你可能认为这些个别的变换并不足以导致如此显著的差异。那么我们如何应用个别变换, 才能理解更复杂的图表呢 ?

Function Transformations: Combined Transformations
::函数转换:组合转换

By combining shifts , reflections , and vertical and horizontal stretches and compression , a simple parent function graph can represent a much more advanced function.
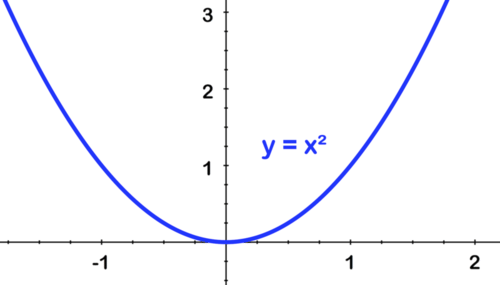
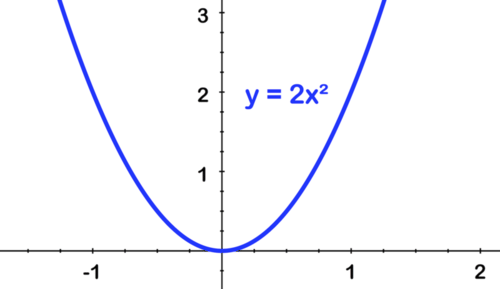
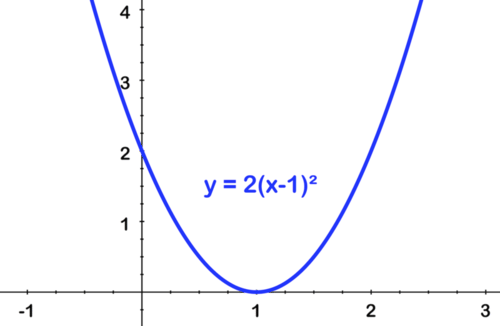
::简单的父函数图形通过将轮班、反射、垂直和水平拉伸和压缩结合起来,可以代表一个更高级的函数。

Consider the equation $\begin{aligned} y = 2 (x - 3)^{2} + 1 \end{aligned}$ . We can compare the graph of this function to the graph of the parent $\begin{aligned} y = x^{2} \end{aligned}$ : the graph represents a vertical stretch by a factor of 2, a horizontal shift 3 units to the right, and a vertical shift of 1 unit.
::考虑y=2(x-33)2+1的方程式。我们可以将此函数的图形与父 y=x2 的图形进行比较: 该图形代表垂直伸展2倍,向右水平移动3个单位,向右垂直移动1个单位。

We can use this relationship to graph the function $\begin{aligned} y = 2 (x - 3)^{2} + 1 \end{aligned}$ . You can start by sketching $\begin{aligned} y = x^{2} \end{aligned}$ or $\begin{aligned} y = 2 x^{2} \end{aligned}$ . Then you can shift the graph 3 units to the right, and up 1 unit.
::我们可以使用此关系来绘制 y=2( x-33)2+1 的函数。您可以先绘制 y=x2 或 y= 2x2 的图示, 然后将图3 单位向右移动, 然后向上移动 1 个单位。

Using your knowledge of the parent function $\begin{aligned} y = | x | \end{aligned}$ and your knowledge of transformations, graph the following function:
::使用您对父函数yx 和您对变换的知识的知识,图解以下函数:

$\begin{aligned} f (x) = - | x | + 3 \end{aligned}$
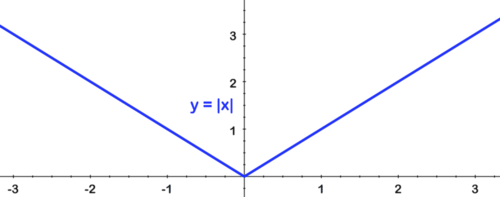
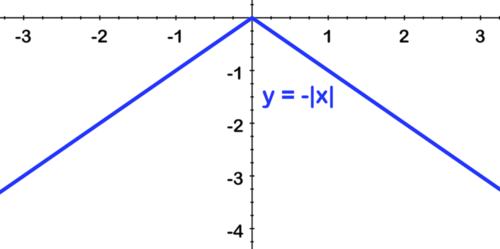
::f(xx) x* 3

The parent graph of this function is the graph of $\begin{aligned} y = | x | \end{aligned}$ , reflected over the $\begin{aligned} x \end{aligned}$ -axis, and shifted up 3 units. The question is: which transformation do you perform first?
::此函数的母图是 yx 的图形, 反映在 x 轴上, 并向上移动了 3 个单位。问题是: 您首先要进行哪种变换 ?

We can answer this question if we consider a few key function values. The table below shows several function values for $\begin{aligned} f (x) = - | x | + 3 \end{aligned}$ :
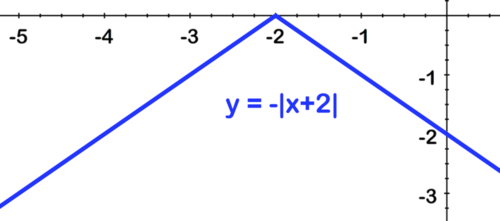
::如果我们考虑几个关键函数值,我们可以回答这个问题。下表显示了 f(x) x 3 的几个函数值:

$\begin{aligned} x \end{aligned}$	$\begin{aligned} f (x) = - a b s (x) + 3 \end{aligned}$
-3	$\begin{aligned} - a b s (- 3) + 3 = - (+ 3) + 3 = - 3 + 3 = 0 \end{aligned}$
-2	$\begin{aligned} - a b s (- 2) + 3 = - (+ 2) + 3 = - 2 + 3 = 1 \end{aligned}$
-1	2
0	3
1	2
3	0

From the function values in the table we can see that the function increases until a vertex at (0, 3), and then it decreases again. This tells us that we can obtain the graph if we first reflect $\begin{aligned} y = | x | \end{aligned}$ over the $\begin{aligned} x \end{aligned}$ -axis (turn the “v” upside down), and then shift the graph up 3 units.
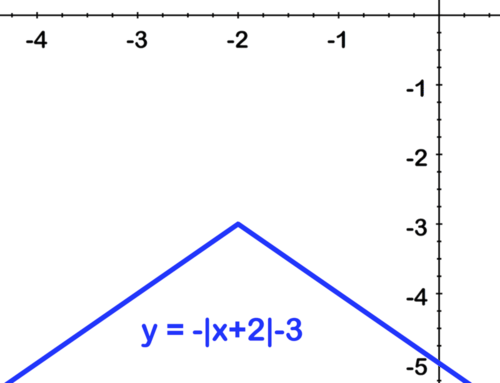
::从表格中的函数值中,我们可以看到函数会增加,直到在(0, 3) 时的顶点,然后又会再次下降。这告诉我们,如果我们首先在 x 轴上反射 yx(将“ v” 向下翻转),然后将图形向上移动 3 个单位, 我们就可以获取图形。

We can also justify this ordering of the transformations of we think about the . To find any function value we take an $\begin{aligned} x \end{aligned}$ value, find its absolute value , find the negative of that number, and then add 3. This is the same as the order of the transformation: reflection comes before shifting up.
::我们还可以解释我们思考的变换顺序。为了找到任何函数值,我们选择了 x 值,找到其绝对值,找到数字的负值,然后添加3。这与变换的顺序是一样的:反省在上升之前就会出现。

When describing the relationship between a transformed graph and its parent graph, it is important to be careful with the order of operations. Take the graph of $\begin{aligned} f (x) = 3 (x + 7)^{3} + 5 \end{aligned}$ and its parent function $\begin{aligned} g (x) = x^{3} \end{aligned}$ .
::当描述一个已转换的图形与其父图形之间的关系时,必须小心操作的顺序。请使用 f(x)=3(x+7)3+5 及其父函数 g(x)=x3 的图形。

The graph of $\begin{aligned} f (x) = 4 (x + 8)^{3} - 3 \end{aligned}$ is the graph of $\begin{aligned} g (x) = x^{3} \end{aligned}$ , stretched vertically (made narrower) by a factor of 3, shifted 7 units to the left, and then shifted 5 units up.
::f( x) = 4( x+8) 3-3 的图形是 g( x) =x3 的图形, 垂直伸展( 缩放) 3 乘以 3, 向左移动 7 个单位, 然后向上移动 5 个单位。

Examples
::实例

Example 1
::例1

Graph the function below using your knowledge of the parent function $\begin{aligned} y = | x | \end{aligned}$ and your knowledge of transformations.
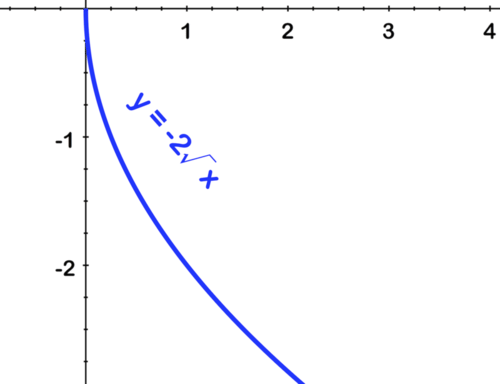
::使用您对父函数 yx 的知识以及您对变换的知识,绘制下面的函数图。

$\begin{aligned} g (x) = | - x + 3 | \end{aligned}$
:xx)x+3}(xx)x+3}

This function represents a horizontal shift of $\begin{aligned} y = | x | \end{aligned}$ , and a reflection over the $\begin{aligned} x \end{aligned}$ -axis. Before graphing, consider a few function values:
::此函数代表 y x 的横向移动和 X 轴的反射。在图形化之前, 请考虑几个函数值 :

$\begin{aligned} x \end{aligned}$	$\begin{aligned} g (x) = a b s (- x + 3) \end{aligned}$
-3	$\begin{aligned} a b s (- (- 3) + 3) = a b s (3 + 3) = a b s (6) = 6 \end{aligned}$
-2	$\begin{aligned} a b s (- (- 2) + 3) = (2 + 3) = a b s (5) = 5 \end{aligned}$
0	3
1	2
3	0
4	1

From the values in the table, we can see that the vertex of the graph is at (3, 0). The graph is shown below.
::从表中的值可以看出,图表的顶点是(3,0),图如下。

The graph looks the same as the graph of $\begin{aligned} y = | x - 3 | \end{aligned}$ . This is the case because $\begin{aligned} y = | - x + 3 | = | - (x - 3) | \end{aligned}$ , and because $\begin{aligned} | - a | = | a | \end{aligned}$ for all values of $\begin{aligned} a \end{aligned}$ , then $\begin{aligned} | - (x - 3) | = | x - 3 | \end{aligned}$ . So the original function is equal to $\begin{aligned} | x - 3 | \end{aligned}$ .
::此图与 yx- 3 { } 的 yx+3 {( x- 3)}} 图表看起来相同。这是因为 yx+3 {( x- 3)}}}}}} , 也因为 a {a {a} 等於 {( x- 3) {} 。因此, 原函数等于 x- 3} 。

We can still think of this graph as a reflection: if we reflect $\begin{aligned} y = | x | \end{aligned}$ over the $\begin{aligned} x \end{aligned}$ -axis, the graph remains the same, as it is symmetric over the $\begin{aligned} x \end{aligned}$ -axis. Then we shift the graph 3 units to the right. What is important to note here is that in order to “read” the equation as a horizontal shift, the entire expression inside the function (in this case, inside the absolute value) must be negated.
::我们仍然可以将这个图表视为一个反射:如果我们在 x 轴上反映 y x , 则该图保持不变, 因为它是 X 轴上的对称。然后我们将图3 单位移到右边。在此必须注意的是, 为了“ 读” 方程式, 如果要进行横向转换, 函数( 在这种情况下, 绝对值内) 的完整表达式必须取消。

Remember that the key to multiple transformations is to do them in order. Another way to keep track of which operations to do in which order is to just do them in the order they appear in the equation, left to right.
::记住多重变换的关键是按顺序进行。另一种方法可以追踪哪些操作可以进行。另一种方法就是按照方程中出现的顺序,从左到右,按顺序进行变换。

Example 2
::例2

Sketch the graph of $\begin{aligned} y = - 3 (x + 2)^{2} + 4 \end{aligned}$
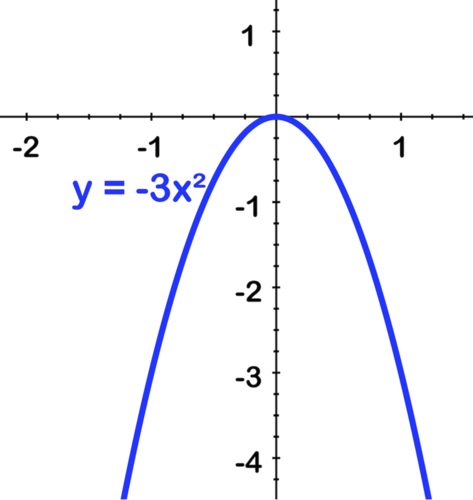
::绘制%3(x+2)2+4的图形

To sketch $\begin{aligned} y = - 3 (x + 2)^{2} + 4 \end{aligned}$ , we start with the parent function, $\begin{aligned} y = x^{2} \end{aligned}$ .
::要绘制 y3( x+2) 2+4, 我们从父函数 y=x2 开始。

First we reflect the function over the $\begin{aligned} x \end{aligned}$ axis:
::首先,我们反映 X 轴上的函数 :

Next we stretch by 3:
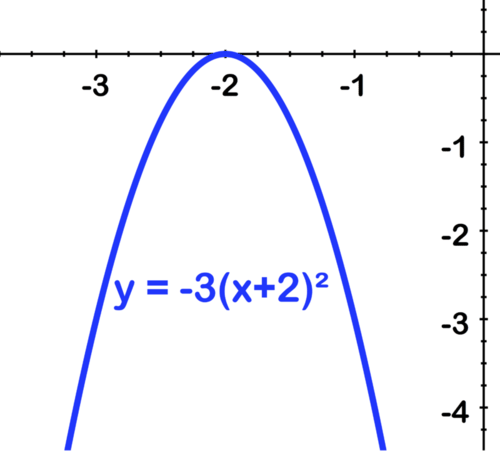
::下一轮我们延长3:

Shift left by 2:
::左移左移 2 :

Finally shift up by 4:
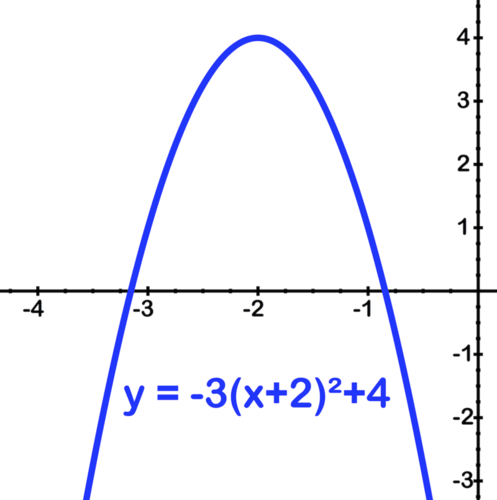
::最后在4点前转移:

Example 3
::例3

Sketch the graph of $\begin{aligned} y = - 1 | x + 2 | - 3 \end{aligned}$
::拼图% 1 @% x+2 @% 3

To sketch $\begin{aligned} y = - 1 | x + 2 | - 3 \end{aligned}$ start with the parent equation: $\begin{aligned} f (x) = | x | \end{aligned}$ and complete the transformations left to right:
::以父方程( f( x) ) 开始绘制 y1 x+23, 完成左向右的转换 :

First reflect over the $\begin{aligned} x \end{aligned}$ axis:
::首先在 x 轴上反射 :

Second, shift left by 2:
::第二,左转2:

Finally, shift down by 3:
::最后,下调3:

Example 4
::例4

Sketch the graph of $\begin{aligned} f (x) = 2 (x - 1)^{2} \end{aligned}$
::从(x) =2 (x- 1) 平铺图

To sketch $\begin{aligned} f (x) = 2 (x - 1)^{2} \end{aligned}$ start with the parent $\begin{aligned} f (x) = x^{2} \end{aligned}$
::草图 f( x) = 2( x- 1) 的 f( x) =x2 , 从父 f( x) =x2 开始

First stretch by 2:
::第一伸展度为 2 :

Second, shift right by 1:
::第二,右转1:

Example 5
::例5

Sketch the graph of $\begin{aligned} f (x) = - 2 \sqrt{x - 1} \end{aligned}$
::将图解从( x)\\\\\\\2x- 1 平移出来

To sketch the graph of $\begin{aligned} f (x) = - 2 \sqrt{x - 1} \end{aligned}$ start with the parent $\begin{aligned} y = \sqrt{x} \end{aligned}$
::绘制 f( x)\\\\\\% 2x- 1 以父 y=x 开头的 f( x)\\\\\ 2x- 1 的图形

First reflect over the $\begin{aligned} x \end{aligned}$ axis:
::首先在 x 轴上反射 :

Second, stretch by 2:
::第二, 伸展至 2 :

Third, shift right by 1:
::第三,右转1:

Review
::回顾

What part of the function $\begin{aligned} g (x) = - (f (x) + 1) = - (x^{3} + 1) \end{aligned}$ shifts the graph of $\begin{aligned} f (x) \end{aligned}$ vertically?
::函数 g( x) ( f( x)+1) ( x3+1) 的哪个部分垂直移动 f( x) 的图形 ?

What part of the function $\begin{aligned} g (x) = - (f (x) + 1) \end{aligned}$ reflects the graph of $\begin{aligned} f (x) \end{aligned}$ across the $\begin{aligned} x \end{aligned}$ -axis?
::函数 g(x) (f(x)+1) 的哪个部分反映 x 轴横跨 x 轴的 f(x) 图形 ?

What is different between the functions $\begin{aligned} g (x) = - (x^{3} + 1.0) \end{aligned}$ and $\begin{aligned} h (x) = - x^{3} + 1.0 \end{aligned}$ that changes the appearance of the graph?
::函数 g( x) ( x3+1.0) 和 h( x)\\\\ x3+1.0 之间有什么不同?

Given the function $\begin{aligned} g (x) = 3.0 (f (x) + 2.0) = 3.0 (x^{2} + 2.0) \end{aligned}$ , what is it that shifts the graph of $\begin{aligned} f (x) \end{aligned}$ vertically?
1. 3.0
2. $\begin{aligned} x^{2} \end{aligned}$
  ::x2x2
3. 2.0
::根据函数 g( x) = 3. 0( f( x) +2. 0) = 3. 0( x2+2. 0) = 3. 0( x2+2. 0) , f( x) 的图形垂直移动的是什么? 3. 0 x2 2. 0

Given the function $\begin{aligned} g (x) = 3.0 (f (x) + 2.0) = 3.0 (x^{2} + 2.0) \end{aligned}$ , what is it that stretches the graph of $\begin{aligned} f (x) \end{aligned}$ vertically?
1. 3.0
2. $\begin{aligned} x^{2} \end{aligned}$
  ::x2x2
3. 2.0
::根据函数 g( x) = 3. 0( f( x) +2. 0) = 3. 0( x2+2. 0) = 3. 0( x2+2. 0) , 垂直伸展 f( x) 图形的是什么? 3. 0 x2 2. 0

What part of the equation $\begin{aligned} k (x) = - (x + 1)^{3} \end{aligned}$ shifts the graph of $\begin{aligned} j (x) = x^{3} \end{aligned}$ horizontally?
::方程式 k( x) ( x+1) 3 的哪个部分水平移动 j( x) = x3 的图形 ?

What part of the equation $\begin{aligned} k (x) = - (x + 1)^{3} \end{aligned}$ reflects the graph of $\begin{aligned} j (x) = x^{3} \end{aligned}$ across the $\begin{aligned} x \end{aligned}$ -axis?
::方程式 k( x) {( x+1) } (x+1) 3 的哪个部分反映 X 轴的 j( x) = x3 的图形 ?

Given the function $\begin{aligned} g (x) = 3.0 (f (x) + 2.0) = 3.0 (x + 2.0)^{3} \end{aligned}$ , what is it that shifts the graph of $\begin{aligned} f (x) \end{aligned}$ horizontally?
::鉴于函数 g( x) = 3. 0( f( x) +2. 0) = 3. 0( x+2. 0) 3, 是什么水平移动 f( x) 的图形 ?

Given the function $\begin{aligned} g (x) = 3.0 (f (x) + 2.0) = 3.0 (x^{2} + 2.0)^{3} \end{aligned}$ , what is it that stretches the graph of $\begin{aligned} f (x) \end{aligned}$ vertically?
::鉴于函数 g( x) = 3. 0( f( x) +2. 0) = 3. 0( x2+2. 0) 3, 垂直延伸 f( x) 图形的是什么 ?

The graph of $\begin{aligned} g (x) \end{aligned}$ is $\begin{aligned} f (x) \end{aligned}$ reflected across the $\begin{aligned} x \end{aligned}$ -axis. The graph of $\begin{aligned} h (x) \end{aligned}$ is $\begin{aligned} f (x) \end{aligned}$ reflected across the $\begin{aligned} y \end{aligned}$ -axis. The graph of $\begin{aligned} j (x) \end{aligned}$ is $\begin{aligned} f (x) \end{aligned}$ reflected across the $\begin{aligned} x \end{aligned}$ -axis and the $\begin{aligned} y \end{aligned}$ -axis. When graphing $\begin{aligned} j (x) \end{aligned}$ does the order in which the reflections occur matter? (Does it matter which axis we reflect the graph across first?)
::g(x) 的图形是 f(x) 。 h(x) 的图形是 f(x) 反射到 y 轴。 j(x) 的图形是 f(x) 反射到 x 轴和 y 轴。当图形显示到 j(x) 时, 反射发生的顺序重要吗? (哪个轴重要吗?)

Given the function $\begin{aligned} f (x) = x^{3} \end{aligned}$ , write a function $\begin{aligned} g (x) \end{aligned}$ that is: $\begin{aligned} f (x) \end{aligned}$ reflected across the $\begin{aligned} y \end{aligned}$ -axis and then stretched vertically by 8.
::根据函数 f( x) =x3, 写一个函数 g( x) , 即: f( x) 反射到 Y 轴, 然后垂直伸展到 8 。

How do you transform the graph of: $\begin{aligned} f (x) = x^{3} \end{aligned}$ so that it looks like the graph of: $\begin{aligned} f (x) = 4 x^{3} + 6 \end{aligned}$ ?
1. Stretch it by a factor of $\begin{aligned} \frac{1}{4} \end{aligned}$ and shift it up 6 units.
  ::将它拉伸14倍,然后将它移到6个单位。
2. Stretch it by a factor of 6 and shift it left 4 units.
  ::将它拉伸6倍,移到4个单元。
3. Stretch it by a factor of 4 and shift it down 6 units.
  ::将它拉伸4乘以4,然后将它移到6个单位。
4. Stretch it by a factor of 4 and shift it up 6 units.
  ::将它拉伸4乘以4,然后将它移到6个单位。
::您如何将 f( x) =x3 的图形转换为 f( x) =x3 +6 的图形 ? 将它平展为 14 乘以 14 乘以 4x3+6 。将它拉伸为 6 乘以 6 乘以 4 乘以 4 乘以 6 乘以。将它拉伸为 4 乘以 4 乘以 6 乘以。

How do you transform the graph of: $\begin{aligned} f (x) = \sqrt{x} \end{aligned}$ so that it looks like the graph of: $\begin{aligned} f (x) = - \sqrt{x} - 4 \end{aligned}$ ?
1. Reflect it across the $\begin{aligned} x \end{aligned}$ -axis and shift it 4 units down.
  ::反射到X轴上然后将4个单位向下移动
2. Reflect it across the $\begin{aligned} y \end{aligned}$ -axis and shift it 4 units up.
  ::反射到Y轴上移动4个单位
3. Reflect it across the $\begin{aligned} x \end{aligned}$ -axis and shift it 4 units up.
  ::反射到X轴上移动4个单位
4. Reflect it across the $\begin{aligned} y \end{aligned}$ -axis and shift it 4 units down.
  ::反射到Y轴上然后将4个单位向下移动
::您如何转换 f( x) =x 的图形, 使其看起来像 f( x) x- 4 的图形 ? 将它反射到 x 轴上, 将其向下移动 4 个单位。将它反射到 y 轴上, 将它向上移动到 4 个单位。将它反射到 x 轴上, 将它向上移动到 y 轴上。将它反射到 y 轴上, 将它向下移动到 4 个单位。

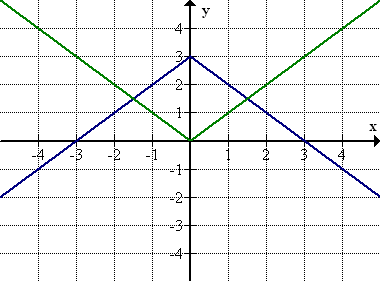
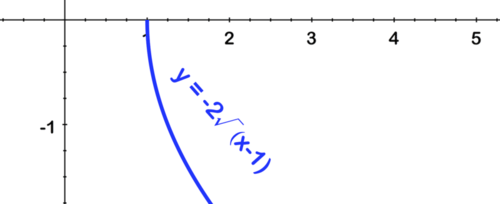
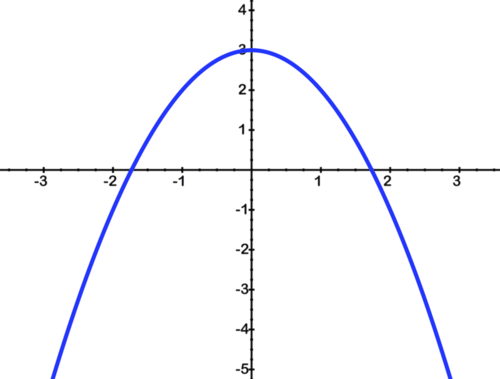
The graph below is a transformation of a common function. What is the common function that has been transformed?
1. $\begin{aligned} y = | x | \end{aligned}$
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
2. $\begin{aligned} y = \sqrt{x} \end{aligned}$
  ::y=x y=x
3. $\begin{aligned} y = x^{2} \end{aligned}$
  ::y=x2 y=x2
4. $\begin{aligned} y = x^{3} \end{aligned}$
  ::y=x3 y=x3
::下图是常见函数的转换。被转换的常见函数是什么? yx y=x y=x2 y=x3

lesson content

How has the function in Q# 14 been transformed?
1. Reflected across the $\begin{aligned} y \end{aligned}$ -axis and shifted right 3 units.
  ::反射到Y轴向右移动3个单位
2. Stretched vertically by a factor of 3 and shifted right 1 unit.
  ::垂直拉伸3倍,右转1单位。
3. Reflected across the $\begin{aligned} x \end{aligned}$ -axis and shifted up 3 units.
  ::反射到X轴移动到3个单位
4. Reflected across the $\begin{aligned} x \end{aligned}$ -axis and shifted left 4 units.
  ::反射到X轴,左转4个单元。
::14 中的函数是如何转换的 ? 反射到 Y 轴和向右移动 3 个单位。垂直拉伸到 3 个乘以 3 , 向右移到 1 个单位。反射到 x 轴, 向上移动到 3 个单位。反射到 X 轴, 向左移动 4 个。

Write a function $\begin{aligned} g (x) \end{aligned}$ whose graph looks like the graph of $\begin{aligned} f (x) = | x | \end{aligned}$ reflected across the $\begin{aligned} x \end{aligned}$ -axis and shifted up 1 unit.
::写入函数 g( x) , 其图形看起来像 f( x) 的图形, 反射到 x 轴, 并移动到 1 个单位。

Choose the function whose graph looks like the graph of $\begin{aligned} f (x) = x^{3} \end{aligned}$ shifted to the right 2 units and reflected across the $\begin{aligned} y \end{aligned}$ -axis.
1. $\begin{aligned} f (x) = (- x - 2)^{3} \end{aligned}$
  :xx) = (-x-2) 3
2. $\begin{aligned} f (x) = (- x + 2)^{3} \end{aligned}$
  :xx)=(-x+2)3
3. $\begin{aligned} f (x) = - (x - 2)^{3} \end{aligned}$
  :xx)(x-2)3
4. $\begin{aligned} f (x) = (x - 2)^{3} \end{aligned}$
  :xx)=(x-2)3
::选择一个函数, 其图形看起来像 f( x) =x3 的图形, 移到右侧 2 单位, 反射到 Y 轴。 f( x) = (- x) = (- x- 2) 3 f( x) = (- x) = (- x+) 2, 3 f( x) = (x-2) 3 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

函数图: 组合转换

Function Transformations: Combined Transformations ::函数转换:组合转换

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)