Course: 1.11 线性、二次曲线和立方体函数模型

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

线性、二次曲线和三次立方函数模型

Learning to express real-life situations as mathematical functions allows seemingly complex ideas and actions to be broken down into smaller, simpler parts and analyzed.
::学习以数学功能来表达现实生活状况,这样就可以将看起来复杂的思想和行动细分为更小、更简单的部分并加以分析。

How might you express the following mathematically?
::你如何用数学表达以下内容?

Two brothers decide to race home from school, taking different routes and each covering a different distance . The second brother leaves 5 minutes after the first, but both arrive at home at the same time.
::两兄弟决定从学校回家,走不同路线,各走不同距离,第二兄弟在第一次离家5分钟后离开,但两人同时回家。

Function Models
::功能模型

Linear Models
::线性模型

A Linear Model uses a linear function (of the form $\begin{align*}y=mx+b\end{align*}$ ) to model a situation of constant change, either increase or decrease.
::A线性模型使用线性函数(y=mx+b)来模拟不断变化的情况,无论是增减。

Say you run a lawn mowing business, and charge $15 per lawn and each lawn mowed cost you about $2 in gas and other expenses. To determine your profit as a function of the number of laws you mow, you can write a function.
::说你们在草坪修剪草坪,每块草坪收费15美元,每块草坪修剪每块草坪花费2美元油费和其他费用。为了根据你们修剪的法律数量来确定利润,你可以写一个函数。

If you express the number of lawns mowed as $\begin{align*}n\end{align*}$ , and your profit as the function "> $\begin{align*}P(n)\end{align*}$ , then:
::如果您将草坪数减为n, 并将利润计为函数P, 那么:

%3D(%5C%2415%20-%20%5C%242)n%3D%5C%2413%20%5C%20n"> $\begin{align*}\text{Profit}=P(n)=(\$15 - \$2)n=\$13 \ n\end{align*}$ . This is a linear model of your profit since it is has the form of a linear function.
::利润=P=(15至2美元)n=13n。这是一个利润的线性模型,因为它具有线性函数的形式。

Quadratic Model
::二次曲线模型

A Quadratic Model uses a quadratic function (of the form $\begin{align*}ax^2+bx+c\end{align*}$ ) to model a situation.
::二次曲线模型使用(xx2+bx+c形式的)二次函数来模拟情况。

Say you are standing on the roof of a building that is 20 feet above the ground. You toss a ball into the air with an initial vertical velocity of 40 ft/sec, so that it will land on the ground, not on the roof. How high will the ball go? When will it reach its maximum height? When will the ball hit the ground?
::说自己站在地上20英尺高的建筑物的屋顶上。你用最初的垂直速度40英尺/秒将一个球扔入空中,以便它降落在地面上,而不是在屋顶上。球会飞到多高?它什么时候会达到最高高度?球什么时候会击中地面?

This situation can be modeled by a quadratic function of the form $\begin{align*}h(t)=-16t^2+v_0t+h_0\end{align*}$ where $\begin{align*}h(t)\end{align*}$ represents the height above the ground and:
::以表 h(t) 16t2+v0t+h0的二次函数来模拟这种情况,其中h(t) 表示地面的高度,并且:

The constant -16 (in units of $\begin{align*}ft/sec^2\end{align*}$ ) comes from the downward force of gravity;
::常数 -16(方英尺/秒2的单位)来自重力向下推力;

$\begin{align*}t\end{align*}$ represents the time (in seconds) since the ball was thrown;
::t 代表球投出后的时间(秒);

$\begin{align*}v_0\end{align*}$ represents the initial velocity (in ft/sec) of the ball, and
::v0 表示球的初始速度(方英尺/秒),以及

$\begin{align*}h_0\end{align*}$ represents the initial height (in ft) of the ball.
::h0 表示球的初始高度( 以英尺计) 。

We can write the function as $\begin{align*}h(t)=-16t^2+40t+20\end{align*}$ .
::我们可以以 h(t)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\+40T+20。

To answer the first and second questions, use your calculator to examine the graph of the function setting a good viewing window, then pressing GRAPH to see the resulting parabola .
::要回答第一个和第二个问题, 请使用您的计算器来检查设置一个良好查看窗口的函数图, 然后按下 GRAPH 来查看由此产生的抛物线。

If you use the MAX function in the CALC Menu, you should find that the coordinates of the vertex are (1.25, 45). This means that 1.25 seconds after the ball is thrown into the air, it reaches a maximum height of 45 feet.
::如果您在 CALC 菜单中使用 MAX 函数, 您应该发现顶点的坐标是(1.25, 45) 。这意味着在球被投入空气后1. 25 秒, 最大高度为 45 英尺。

To answer the third question, we need to determine when the height of the ball is 0. Graphically, we are looking for the $\begin{align*}x\end{align*}$ - intercept of the parabola. If we want to determine the exact value, we can use the ZERO function of the calculator or just solve the quadratic equation for the two intercepts . Using either method, you should find that the $\begin{align*}x\end{align*}$ -intercept is approximately 2.93. This means that the ball reaches the ground in just under 3 seconds.
::回答第三个问题, 我们需要确定球的高度是 0 。从图形上看, 我们正在寻找 parbola 的 X inter 。如果我们想要确定准确值, 我们可以使用计算器的 ZERO 函数, 或者只解决两个截取器的四方方程。使用这两种方法, 您应该发现 X inter 大约是 2. 93 。这意味着球在三秒内到达地面。

Cubic Model
::Cucc 模型

A Cubic Model uses a cubic functions (of the form $\begin{align*}ax^3+bx^2+cx+d\end{align*}$ ) to model real-world situations. They can be used to model three-dimensional objects to allow you to identify a missing dimension or explore the result of changes to one or more dimensions .
::立方体模型使用一种立方函数( 以x3+bx2+cx+d形式) 来模拟真实世界环境。它们可以用来模拟三维天体, 以便您识别缺失的维度或探索一个或一个以上维的变化结果。

Consider a situation in which a rectangular piece of cardboard is folded into a box. The folding is made possible by cutting squares out of the four corners of the cardboard.
::考虑一下纸板的长方形片被折叠成盒子的情况。折叠是通过切开纸板四角的方形而得以实现的。

Calculate the maximum volume possible of a box made from a sheet of cardboard $\begin{align*}12^{\prime \prime} \times 8^{\prime \prime}\end{align*}$ .
::计算用纸板 12+8+++++++++++++++++++++++++++++++++++++++++12++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ 制成的纸盒的最大容量。

The function $\begin{align*}v(x) = (12 - 2x)(8 - 2x)x\end{align*}$ could be used to represent the volume of the box as a function of $\begin{align*}x\end{align*}$ , the side-length of the squares cut out of the corners. If we multiply out the factors of this function we can verify that this is a cubic function:
::函数 v (x) = (12) - 2x (8 - 2x) x 可用于代表框的音量, 以 x 的函数表示角切开的方形的侧长。如果我们乘出此函数的因子, 我们就可以核实这是立方函数 :

$\begin{align*}v(x) = (12 - 2x)(8 - 2x)x = 4{x^3} - 40{x^2} + 96x\end{align*}$
:

x) = (12- 2x) 8- 2x) x= 4x3 - 40x2+96x

We can analyze the graph of the function to find the maximum possible volume of the box. When analyzing the function to determine the maximum volume of the box, we only look at the portion of the graph where $\begin{align*}x\end{align*}$ is no greater than 4. If we cut out $\begin{align*}\{4 \times 4 \}\end{align*}$ squares, we would cut out the entire short side of the cardboard rectangle, and we would not be able to make a box. Focusing then on the interval (0, 4) we can see that the volume of the box increases, and then decreases. The graphing calculator can be used to determine that when $\begin{align*}x\end{align*}$ is 1.57 in, the volume of the box is maximum at $\begin{align*}67.60 \ in^3\end{align*}$ .
::我们可以分析函数的图形以找到盒子的最大可能的体积。当分析函数以决定盒子的最大体积时, 我们只能查看图表中 x 不大于 4 的部位。如果我们切除 {4x4} 方形, 我们就会切除纸板矩形的整个短侧, 并且我们无法做出一个框。聚焦于间隔 (0, 4) 时, 我们可以看到盒子的体积会增加, 然后下降。图形计算器可以用来确定当 x 是 1. 57 时, 盒子的体积最多为 67. 60 3 时。

Examples
::实例

Example 1
::例1

Earlier, you were to mathematically model a situation with two brothers who decided to race home from school taking different routes. The second brother leaves 5 minutes after the first, and both arrive at home at the same time.
::早些时候,你在数学上模拟了两个兄弟的情况,他们决定通过不同路线从学校赛跑回家,第二兄弟在第一次离家5分钟后离开,两人同时回家。

There are a number of different ways to model the information, depending on what part(s) of the information you choose to use. A couple of examples include:
::根据您选择使用的信息的哪一部分,有多种不同的信息模式。

If $\begin{align*}t\end{align*}$ = the time the second brother took to get home and the distance he ran is, then $\begin{align*}t+5\end{align*}$ = the time the first brother took.
::如果t=第二兄弟回家的时间和他跑的距离,那么t+5=第一兄弟回家的时间。

If $\begin{align*}t\end{align*}$ = the time the first brother took to get home, then $\begin{align*}\frac{(t + (t - 5))}{2}\end{align*}$ represents the average time to run home.
::如果t = 第一兄弟回家的时间,那么(t+(t-5))2 表示平均回家时间。

Your model may be similar, or may be written differently, but should compare different values given in the story problem .
::您的模型可能是相似的, 也可能是不同的写法, 但应该比较故事问题中给出的不同值。

Example 2
::例2

The Arlington Freshmen class wants to have a fundraiser. The class wants to buy a number of $4.00 flip-flops and $5.00 baseball hats, and has a total of $100 to spend.
::阿林顿新人班想要一个筹款活动。该班想买几个四块的翻滚鞋和五块的棒球帽,总共要花100美元。

If $\begin{align*}f\end{align*}$ represents the number of flip-flops and $\begin{align*}h\end{align*}$ represents the number of baseball hats, write a function to represent the number of flip-flops purchased as a function of unspent monies from baseball hats.
::如果 f 表示翻滚式拖车数目, h 表示棒球帽数目,请写一个函数,表示以棒球帽未用钱为函数购买的翻滚式拖车数目。

Using your equation from part 1, determine the number of baseball hats that can be bought if 10 flip flops were purchased.
::使用第1部分的方程式确定棒球帽的数量如果购买了10个翻滚球就可以买到多少个棒球帽

To express this information as a function, remember that the question specified that there was $100 to spend, and that any money not spent on hats (at $5 ea) was spent on flip-flops (at $4 ea).
::为了将这一信息作为一种功能来表达,请记住,问题明确指出,有100美元需要支出,任何未花在帽子上的钱(5美元ea)都花在翻转拖车上(4美元ea)。

$\begin{align*}4f + 5h = 100\end{align*}$ is the basic equation that balances purchases and available money. This means: $\begin{align*}f = - \frac{5}{4}h + 25\end{align*}$ .
::4f+5h=100是平衡购买和可用资金的基本方程式。这意味着:f54h+25。

To calculate how many hats could be bought if 10 pairs of flip flops were purchased, substitute 10 in for $\begin{align*}f\end{align*}$ , and solve for $\begin{align*}h\end{align*}$ :
::计算如果购买了10对翻转滑杆,可以购买多少帽子,f替代10顶帽子,然后解决h:

$\begin{align*}10 &=\frac{100-5h}{4} \\ 40 &=100-5h \\ 5h &=60 \\ h &=12 \end{align*}$
::10=100-5h440=100-5h5h5h=60h=12

Therefore , if 10 pairs of flip flops were purchased, there would be money left over to buy 12 baseball caps.
::因此,如果购买了10双翻滚杆,就剩下钱来购买12个棒球帽。

Example 3
::例3

Studies of the metabolism of alcohol consistently show that blood alcohol content (BAC) declines linearly, after rising rapidly after initial ingestion. In one study, BAC in a fasting person rose to about 0.018 % after a single drink. After an hour the level had dropped to 0.010 %.
::对酒精新陈代谢的研究始终表明,血液酒精含量(BAC)在初步摄入后迅速上升后直线下降。在一项研究中,禁食者的酒精含量(BAC)在一次饮酒后上升至0.018 % 。一小时后水平下降到0.010%。

Write an equation relating BAC to time in hours after drinking $\begin{align*}t\end{align*}$ .
::写一个方程式,将BAC与饮T后几个小时的时间联系起来。

Assuming that BAC continues to decline linearly (meaning at a constant rate of change), approximately when will BAC drop to 0.002%?
::假设BAC继续线性下降(即以不变的变动率),BAC大约何时会下降到0.002%?

In order to answer the question, you must express the relationship as an equation and then use the equation.
::为了回答这个问题,你必须把关系表达为等式,然后使用等式。

First, define the variables in the function and create a table.
::首先,定义函数中的变量并创建表格。

The two variables are time and BAC.
::这两个变量是时间和BAC。

Time ::时间时间时间时间时间时间时间时间时间	BAC ::BAC BAC
0	0.018%
1	0.010%

Next, calculate the rate of change .
::接下来,计算变化率。

Time ::时间时间时间时间时间时间时间时间时间	BAC ::BAC BAC	Rate of change ::变化率变化率
0	0.018%	0
1	0.010%	(0.008%)

This rate of change means when the time increases by 1, the BAC decreases (since the rate of change is negative) by .008. In other words, the BAC is decreasing .008% every hour. Since we are told that BAC declines linearly, we can assume that figure stays constant.
::这一变化率意味着当时间增加1:1时,BAC就会下降(因为变化率是负的)0.008时,换句话说,BAC每小时下降0.008 % 。由于我们被告知BAC线性下降,我们可以假设这个数字保持不变。

Now we can write an equation with $\begin{align*}b\end{align*}$ representing BAC and $\begin{align*}t\end{align*}$ the time in hours:
::现在我们可以用 b 代表 BAC 来写一个方程式,

$\begin{align*}b=-.008t+.018\end{align*}$
::b.008t+.018

To learn when will the BAC reach .002%, substitute .002 in for $\begin{align*}b\end{align*}$ and solve for $\begin{align*}t\end{align*}$ .
::学习BAC何时能达到0.002%, 替换0.002%到b, 解决 t。

$\begin{align*}.002 &=-.008t+.018 \\ -.016 &=-.008t \\ t &=2 \end{align*}$
::0008t+.018 -.016\.008t=2

Therefore the BAC will reach .002% after 2 hours.
::因此,BAC在2小时后将达到0.002%。

Example 4
::例4

What is the maximum volume of an open-top box, made from a square piece of cardboard with an area of 64 sf?
::开口纸箱的最大体积是多少? 纸板的平方块,面积为64 sf 。

Assuming the box is made by cutting squares from each corner to allow the sides to fold up, what are the dimensions of those square cut-outs?
::假设盒子是用从每个角落切开的方形来制造以便让两边折叠, 那么这些方形隔断的尺寸是多少?

What interval on the graph is pertinent to this particular question?
::图表上哪些间隔与这个特定问题相关?

Let $\begin{align*}s\end{align*}$ represent the side length of each square cut out of a corner, then the dimensions of the box will be $\begin{align*}8-2s\end{align*}$ , $\begin{align*}8-2s\end{align*}$ and $\begin{align*}s\end{align*}$ , for length, width, and height, respectively.
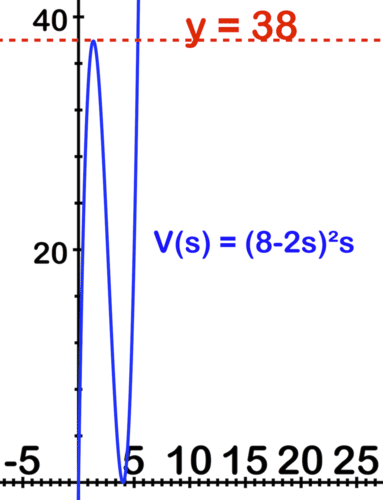
::s 表示从角处切开的每个方形的侧长,然后框的尺寸将分别为长度、宽度和高度8-2s、8-2s和s。

The volume of the box as a function of side length: $\begin{align*}V(s)=(8-2s)(8-2s)s \end{align*}$
::边长函数的框体积: V(s) =(8)-2s(8)-2s(8)s

Graph this on a graphing calculator to see the function:
::在图形计算计算器上绘制此图,以查看函数 :

The maximum volume is approximately 38 cu ft.
::最大体积约为38公尺。

The square corners are approximately 1.3 ft on each side
::每一边的广场角大约为1.3英尺

The interval: (0, 4) contains all possible side lengths, since sides cannot be zero or negative, and 4 or more feet cannot be cut twice from 8 feet.
::间隔: (0, 4) 包含所有可能的侧边长度, 因为两边不能为零或负, 4英尺或4英尺以上不能从8英尺切开两次。

Example 5
::例5

The profits for a business can be determined by subtracting the costs from the revenue . Suppose the revenue of a business is modeled by the function $\begin{align*}R(x)=5x-0.01x^2\end{align*}$ , and the costs of manufacturing the product is modeled by $\begin{align*}C(x)=100+2x\end{align*}$ , where $\begin{align*}x\end{align*}$ is the number of units of the product.
::企业的利润可以通过从收入中减去成本来确定。假设企业的收入以函数R(x)=5x-0.01x2为模型,而产品的制造成本则以C(x)=100+2x为模型,其中x是产品单位的数量。

Write a function $\begin{align*}P(x)\end{align*}$ to model the company’s profits.
::撰写函数 P(x) 来模拟公司的利润。

$\begin{align*}P(x)=R(x)-C(x)=-0.01x2+3x-100\end{align*}$
::P(x) = R(x) = C(x) = 0.01x2+3x- 100

Graph $\begin{align*}P(x)\end{align*}$ and determine the maximum profit.
::图P(x)和确定最大利润。

The maximum profit is 125 (usually in thousands, or another larger unit!)
::最大利润125(通常以千计, 或以另一大单位! )

Review
::回顾

From 2002 - 2009 the number of gas stations in a certain country increased by 100 stations per year. In 2004 there were 1100 gas stations. Write a linear equation for the number of gas stations, "> $\begin{align*}(y)\end{align*}$ , as a function of time, $\begin{align*}(t)\end{align*}$ , where $\begin{align*}t=0\end{align*}$ represents the year 2002.
::从2002年至2009年,某些国家的加油站数量每年增加100个,2004年有1100个,为加油站数量写一个线性方程,按时间函数,(t),t=0代表2002年。

For #2-3, find the vertex of the quadratic functions and then graph them.
::在# 2-3 中, 找到二次函数的顶点, 然后绘制图表。

$\begin{align*}f(x)=2x^2-6x+11\end{align*}$
:xx) = 2x2 - 6x+11

$\begin{align*}f(x)=3(x+5)^2-2\end{align*}$
:xx)=3(x+5)2-2

At the local downtown 4th of July fireworks celebration, the fireworks are shot by remote control into the air from a pit in the ground that is 12 feet below the earth's surface.
1. Find an equation that models the height of an aerial bomb $\begin{align*}t\end{align*}$ seconds after it is shot upwards with an initial velocity of 80 ft/sec. Assume that the bomb decelerates at a rate of 30 ft/sec each second
  ::找到一个方程式,该方程式在空投炸弹射向向上以最初速度80立方英尺/秒的速度向上射出后几秒,以其高度为模型。假设炸弹以每秒30立方英尺/秒的速度减速
2. Find the vertex of the quadratic function.
  ::查找二次函数的顶点。
3. What is the maximum height above ground level that the aerial bomb will reach?
  ::空中炸弹达到的地面最高高度是多少?
4. How many seconds after it was launched will it take to reach that height?
  ::发射几秒后才能达到那个高度?
::在7月4日当地市区的烟火节上,烟火是从地面下方12英尺处的坑子遥控射入空中的。找到一个方程式, 以最初80英尺/ sec 的速度, 模拟空中炸弹射向上方的高度。假设炸弹以每秒30英尺/ sec 的速度减速, 发现二次函数的顶部。空中炸弹到达地面最高高度是多少? 发射后需要多少秒才能达到这一高度?

A rock is thrown from the top of a 763 ft tall building. The distance, in feet, between the rock and the ground $\begin{align*}t\end{align*}$ seconds after it is thrown is given by $\begin{align*}d=-16t^2-2t+763\end{align*}$ . How long after the rock is thrown is it 430 feet from the ground?
::岩石从763英尺高的建筑物顶部被抛出。岩石抛出后几秒钟,岩石与地面之间的距离是d16t2-2-2t+763。岩石抛出后多久,离地面有430英尺?

Use the vertical motion formula $\begin{align*}h=-16t^2+v_ot+s\end{align*}$ to find the number of seconds it takes for a rocket launched from the ground with a starting velocity of 96 ft/s to reach an altitude of 45 ft. Round answers to the nearest tenth.
::使用垂直运动公式 h16t2+vot+s 来寻找从地面发射火箭所需的秒数,该火箭的起始速度为96英尺/秒,以达到接近十分之一的45英尺高度。

The function $\begin{align*}P = 0.0089{t^2} + 1.1149t + 78.4491\end{align*}$ models the United States population in millions since 1900. Use the function $\begin{align*}P\end{align*}$ to predict the year in which the population exceeds 1 billion.
::P=0.0089t2+1.1149t+78.4491 函数模拟自1900年以来美国人口以百万计。使用P函数预测人口超过10亿的年份。

For which value of $\begin{align*}x\end{align*}$ is $\begin{align*}f(x)=-10\end{align*}$ if $\begin{align*}f(x)=-4x^2+3x\end{align*}$ ?
::如果 f( x)\\\\\\\\\\\\\\\\\2+3x, x 的值是 f( x)\\\\\\\ 10, 那么 x的值是 f( f)\\\\\\\\ x2+3x ?

A box is to be made by cutting squares out of the corners of a rectangular piece of cardboard. The dimensions of the cardboard are $\begin{align*}n\end{align*}$ inches by $\begin{align*}m\end{align*}$ inches. Assume that $\begin{align*}n>m\end{align*}$ .
1. Write a model for the volume of the box.
  ::为盒子的体积写一个模型。
2. What is the largest square that can be cut out of the corners of the cardboard?
  ::从纸板角落切开的最大方块是什么?
::框要用切开的方形隔开纸板的角。纸板的尺寸每英寸为 n 英寸。假设 n>m 。写一个框体积的模型。最大的方形是什么样的方形可以切开纸板的角?

Suppose you were told that you could use a single sheet of paper for notes on your math final. The instructor says that you may use any sheet you like, but the shape must be a quadrangle and the perimeter may not exceed 45 in.
1. What dimensions should you use to provide the greatest area for your notes?
  ::您应该使用什么维度来提供您笔记的最大区域 ?
2. How does a graphing calculator help to simplify this question?
  ::图形化计算器如何帮助简化这一问题?
::假设有人告诉您, 您数学决赛的笔记可以使用一张纸。教官说您可以使用任何您喜欢的笔记, 但形状必须是一个矩形, 周界不能超过45个。您应该使用什么维度来提供您笔记的最大区域 ? 图形计算器如何帮助简化这个问题 ?

Is $\begin{align*}f(x)=-3^{4x}\end{align*}$ a power function?
::f( x)\\\\\\\\\34x 是一个功率函数吗 ?

Is $\begin{align*}f(x)=\sqrt[3]{8x^5}\end{align*}$ a power function?
::f( x) = 38x5 是一个功率函数吗 ?

Is $\begin{align*}g(x)=7 \cdot 2^x\end{align*}$ a power function? If not, why not?
::g(x) = 72x 是一个功率函数吗? 如果没有,为什么不呢?

Is $\begin{align*}h(x)=2x^{-5}\end{align*}$ a power function? If not, why not?
::h(x)=2x-5 是一个功率函数吗? 如果没有,为什么不呢?

The volume $\begin{align*}v\end{align*}$ of a sphere varies directly as the cube of the radius $\begin{align*}r\end{align*}$ . When the radius of a sphere is 6 cm, the volume is $\begin{align*}904.779 \ cm^3\end{align*}$ . What is the radius of a sphere whose volume is $\begin{align*}268.083 \ cm^3\end{align*}$ ?
::当一个球的半径为 6 厘米时, 体积为 904. 779 厘米。体积为 268. 083 厘米的球体的半径是 268. 083 厘米?

The force of gravity $\begin{align*}(F)\end{align*}$ acting on an object is inversely proportional to the square of the distance $\begin{align*}d\end{align*}$ from the object to the center of the earth. Write an equation that models this situation.
::重力(F)在物体上作用的强度与从物体到地球中心的距离的正方形成反比。写一个公式来模拟这种情况。

Sue and Betty gathered the data in the table below using a 100-watt light bulb and a Calculator-Based Laboratory(CBL) with a light-intensity probe.
::Sue和Betty用100瓦灯泡和以计算器为基础的实验室(CBL)和光强度探测器收集了下表的数据。

Light Intensity Data for a 100w light bulb
::100w光灯泡的光强度数据

*Distance $\begin{align}(m)\end{align}$* ::距离(m)	*Intensity $\begin{align}(W/m^2)\end{align}$* ::强度(W/m2)
1.0	7.95
1.5	3.53
2.0	2.01
2.5	1.27
3.0	0.90

Use your calculator to find the power regression model of the data.
::使用您的计算器查找数据的功率回归模型。

Describe the relationship between the intensity and distance modeled with the equation.
::描述用方程式建模的强度和距离之间的关系。

Use the regression model to predict the intensity of an object 2.75 meters away.
::使用回归模型预测2.75米外物体的强度。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

线性、 二次曲线和三次立方函数模型

Function Models ::功能模型

Linear Models ::线性模型

Quadratic Model ::二次曲线模型

Cubic Model ::Cucc 模型

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源