Course: 2.9 职能的连续性

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section a 职能的连续性

Collapse Expand
a 职能的连续性
The is related to the conceptual notion of a function not having any breaks or sudden jumps as the independent variable takes on all values over some interval. There are no range gaps, or sudden jumps over the domain of interest. With this in mind, see if you can determine which of the following could be considered to represent a continuous function:
::与函数没有间断或突然跳动的概念有关,因为独立变量在一定间隔内吸收了所有值。没有范围差, 或在利益领域上突然跳跃。有鉴于此, 请看您能否确定以下哪些函数可以被视为代表连续函数 :

daily outdoor temperature variation
::每日户外温度变化

weight of a cart as 10 lb bags of sand are loaded on it
::装满10磅沙袋的马车重量

the rise and fall of the level of a reservoir of water
::水库水量水平的上升和下降

the amount of money collected at a movie theater for a specific showing.
::在一个电影院里为某场特别表演募集的金额

Continuity
::连续连续性

Continuity of a function is conceptually the characteristic of a function curve that has the values of the range “flow” continuously without interruption over some interval, as if never having to lift pencil from paper while drawing the curve. This intuitive notion needs to be formalized mathematically.
::从概念上讲,函数的连续性是功能曲线的特点,它具有“流动”范围值,在一定的间隔内不间断地不间断地保持,仿佛在绘制曲线时从未从纸上抬起铅笔。这个直观概念需要数学形式化。

Consider the graph of the function $\begin{align*}f(x)=x^2\end{align*}$ . The function is defined for any real value of the independent variable.
::考虑函数 f( x) =x2 的图形。函数是根据独立变量的任何真实值定义的。

For example, for $\begin{align*}x=2\end{align*}$ the function has the value $\begin{align*}f(2)=4\end{align*}$ . Notice that as $\begin{align*}x\end{align*}$ approaches the value 2 from either the left or the right, the value of the function approaches 4, i.e., $\begin{align*}\lim_{x \to 2} f(x)=f(2)=4\end{align*}$ . Conceptually, applying the left and right as $\begin{align*}x\end{align*}$ approached 2, resulted in the same value, the value of the function at $\begin{align*}x=2\end{align*}$ .
::例如,对于 x=2, 函数具有 f(2)=4. 值。请注意, 当 x 从左边或右边接近值 2 时, 函数的值向4 , 即 limx% 2f(x)=f(2)=4. 。从概念上说, 将左和右与 x 向2 相乘, 得出相同值, x=2 的函数值与 x=2 相同。

The above results illustrate key properties of a continuous function. They are formalized in the following definition that provides a test for determining when we have a continuous function.
::上述结果说明了持续性职能的关键特性,并在以下定义中加以正式确定,该定义为确定我们何时具有持续性职能提供了检验标准。

The function $\begin{align*}f(x)\end{align*}$ is continuous at $\begin{align*}x=a\end{align*}$ if the following conditions all hold:
::函数 f( x) 在 x=a 时是连续的, 如果下列条件都保持 :

$\begin{align*}a\end{align*}$ is in the domain of $\begin{align*}f(x)\end{align*}$ ;
::a 在 f(x) 的域内;

$\begin{align*}\lim_{x \to a} f(x)\end{align*}$ exists;
:x) 存在limxaf(x) ;

$\begin{align*}\lim_{x \to a} f(x)=f(a)\end{align*}$
::limxaf(x) = f(a)

Note that it is possible to have functions where two of these conditions are satisfied but the third is not. When a function is not continuous at $\begin{align*}x=a\end{align*}$ , then it is discontinuous at $\begin{align*}a\end{align*}$ , and $\begin{align*}a\end{align*}$ is a point of discontinuity.
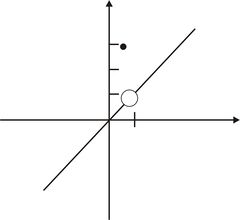
::请注意,如果满足其中两个条件,但第三个条件不满足,则可能具有功能。如果在 x=a 时函数不是连续的,则在a 时是不连续的,并且是一个不连续的点。

Consider the piece-wise function $\begin{align*}f(x)= \begin{cases} x, \mbox{if} \ x \neq 1\\ 3, \mbox{if} \ x=1 \end{cases}\end{align*}$ , with the graph shown below.
::以下面的图表来考虑 pief-wise 函数 f( x)\\\\ x,if x\\\\\\13,if x=1 。

In this example, we have $\begin{align*}\lim_{x \to 1} f(x)\end{align*}$ exists! The value $\begin{align*}x=1\end{align*}$ is in the domain of $\begin{align*}f(x)\end{align*}$ , but $\begin{align*}\lim_{x \to 1} f(x) \neq f(1)\end{align*}$ . Therefore the function is not continuous at $\begin{align*}x=1\end{align*}$ .
::在此示例中, 我们存在 limx% 1f( x) ! 值 x=1 是在 f( x) 的域内, 但 limx% 1f( x) \\\\\ f (1) 。因此, 函数在 x=1 时不连续。

This is an example of a removable discontinuity , i.e., a discontinuity at which the limit of the function exists but does not equal the value of the function at that point.
::这是可移动的不连续性的一个实例, 即函数的极限存在但不等于该函数在当时的价值的不连续性。

Consider the following function: $\begin{align*}f(x)=\frac{(x+1)}{(x^2-1)}\end{align*}$ . Are there any discontinuities?
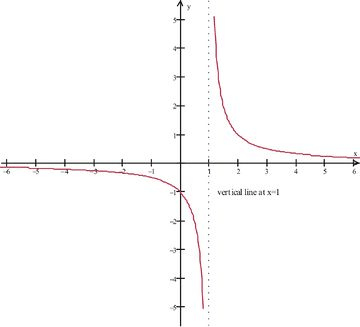
::考虑以下函数 : f( x) = (x+1) (x2- 1) 。有没有不连续?

We know from our study of domains that in order for the function to be defined, we must have $\begin{align*}x \neq -1,1\end{align*}$ . Yet when we generate the graph of the function (using the standard viewing window), we get the following picture that appears to be defined at $\begin{align*}x=-1\end{align*}$ :
::我们从对域的研究中知道,为了定义函数,我们必须有 x1,1。然而,当我们(使用标准查看窗口)生成函数图时,我们得到以下图象,图象似乎在 x1中定义:

The apparent contradiction is due to the fact that our original function had $\begin{align*}x+1\end{align*}$ as a common factor in the numerator and denominator, which cancelled out and gave us a picture that appears to be the graph of $\begin{align*}f(x)=\frac{1}{(x-1)}\end{align*}$ .
::明显自相矛盾的原因是,我们的原始函数在分子和分母中以x+1为共同系数,而该分母和分母取消并给了我们一张图片,似乎是f(x)=1(x)-1的图形。

But what we actually have is the original function, $\begin{align*}f(x)=\frac{(x+1)}{(x^2-1)}\end{align*}$ that we know is not defined at $\begin{align*}x=-1\end{align*}$ . At $\begin{align*}x=-1\end{align*}$ , we have a hole in the graph, or a discontinuity of the function at $\begin{align*}x=-1\end{align*}$ . That is, the function is defined for all other $\begin{align*}x\end{align*}$ -values close to $\begin{align*}x=-1\end{align*}$ .
::但是,我们实际上拥有的是我们所知道的初始函数 f(x) = (x+1)(x2- 1) 的 f(x) = (x+1) (x2- 1) 。在 x\\\ 1. 时, 图形有一个洞, 或者在 x\\\ 1 时, 函数的不连续。也就是说, 该函数被定义为所有接近 x+1 的其他 x 值。

In addition, at $\begin{align*}x=1\end{align*}$ the function values go to $\begin{align*}\pm \infty\end{align*}$ depending on which side of $\begin{align*}x=1\end{align*}$ is used. The right and left one-sided limits will not be the same, and the function is discontinuous at $\begin{align*}x=1\end{align*}$ . The discontinuity at $\begin{align*}x=1\end{align*}$ is called an infinite discontinuity and is associated with the vertical asymptote $\begin{align*}x=1\end{align*}$ .
::此外,在 x=1 时,函数值根据 x=1 的哪一面使用 \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x=1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x=1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Loosely speaking, if we were to hand-draw the graph, we would need to take our pencil off the page when we got to this hole, leaving a gap in the graph as indicated:
::粗略地说,如果我们手工绘制图表,当我们到达这个洞口时,我们需要把铅笔从页面上拿掉,在图表中留下一个空白,如所示:

Examples
::实例

Example 1
::例1

Earlier, you were asked which of the following could be considered to represent a continuous function:
::早些时候,有人问您,可以认为以下哪一种职能是持续性职能:

daily outdoor temperature variation
::每日户外温度变化

weight of a cart as 10 lb bags of sand are loaded
::装满10磅袋沙袋的推车重量

the rise and fall of the level of water in a reservoir
::水库水位的上升和下降

the amount of money collected at a movie theater for a specific showing
::在一个电影院里为某个特定表演募集的金额

The daily outdoor temperature variation could be considered a continuous function of time as because all temperature values occur in the range of variation.
::每日户外温度变化可被视为时间的连续函数,因为所有温度值都发生在变化范围之内。

The weight of a cart as 10 lb bags of sand are loaded would not be considered a continuous function of the number of bags because only integer numbers of bags are possible and the total weight changes in 10 lb increments, so there are gaps.
::装满10磅沙袋的马车重量不会被视为袋数的连续函数,因为只有整数的袋子是可能的,总重量变化是10磅递增的,因此有差距。

The rise and fall of the level of water in a reservoir could be considered continuous function of time because all levels occur in the range of variation.
::水库水位的上升和下降可被视为时间的连续功能,因为所有水位的变化范围各不相同。

The amount of money collected at a movie theater for a specific showing would not be considered a continuous function since the number of people buying and the price per ticket are integers so that only certain total dollar amounts are possible.
::在电影院为某个特定表演所募集的钱款数额不会被视为一种持续功能,因为购买人数和每张票的价格都是从电影院买来的,因此只有一定的美元总额是可能的。

Example 2
::例2

Find a value of $\begin{align*}k\end{align*}$ which makes the following function continuous:
::查找使以下函数连续的 k 值 :

$\begin{align*}f(x) = \begin{cases} kx+1, & x \le 3 \\ -(5-x)^3, & x>3 \end{cases}\end{align*}$
::f( x) kx+1, x%3-( 5- x) 3, x>3

If $\begin{align*}f(x)\end{align*}$ is to be considered continuous everywhere, it must be continuous at $\begin{align*}x=3\end{align*}$ . This means that:
::如果f(x)在任何地方被视为连续连续,必须在x=3时连续,这意味着:

$\begin{align*}x=3\end{align*}$ must be in the domain of $\begin{align*}f(x)\end{align*}$ ; it is.
::x=3 必须位于 f( x) 的域内; 确实如此。

$\begin{align*}\lim_{x \to 3^-} f(x)=\lim_{x \to 3^+} f(x)\end{align*}$ so that $\begin{align*}\lim_{x \to 3} f(x)\end{align*}$ would exist; which means the following equality must hold:
::立方公尺x3-f(x)=limx3+f(x),以便存在立方公尺x3-f(x),这意味着必须保持以下平等:

$\begin{align*}k(3)+1=-(5-3)^3\end{align*}$ , and $\begin{align*}k=-3\end{align*}$ .
::k(3)+1(5-3)3和k3。

Then $\begin{align*}\lim_{x \to 3} f(x)=-8\end{align*}$
::然后 lix_3f( x) @%% 8

With the above result, we have $\begin{align*}\lim_{x \to 3} f(x)=-8=f(-3)\end{align*}$ .
::有了上述结果,我们有了立方厘米3f(x)8=f(3))。

Therefore, the function $\begin{align*}f(x) = \begin{cases} -3x+1, \quad x \le 3 \\ -(5-x)^3, \ x>3 \end{cases}\end{align*}$ is continuous at $\begin{align*}x=3\end{align*}$ .
::因此,函数 f(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x>3 x>3 在 x=3 时是连续的。

Example 3
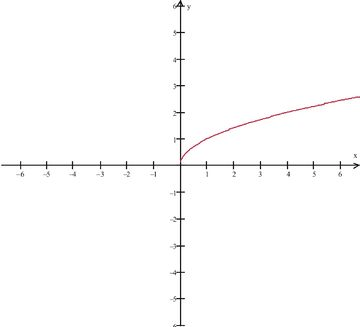
::例3

Let’s recall our basic square root function, $\begin{align*}f(x)=\sqrt{x}\end{align*}$ , shown below. Is it continuous at $\begin{align*}x=0\end{align*}$ ?
::让我们回顾下面显示的基本平方根函数 f( x) x。 x=0时是否连续?

Since the domain of $\begin{align*}f(x)=\sqrt{x}\end{align*}$ is $\begin{align*}x \ge 0\end{align*}$ , we see that $\begin{align*}\lim_{x \to 0} \sqrt{x}\end{align*}$ does not exist . Specifically, we cannot find open intervals around $\begin{align*}x=0\end{align*}$ that satisfy the limit definition. Therefore, the function is not continuous at $\begin{align*}x=0\end{align*}$ . However we do note that as we approach $\begin{align*}x=0\end{align*}$ from the right-hand side, we see the successive values tending towards $\begin{align*}x=0\end{align*}$ .
::由于 f( x) x 的域为 x=0, 我们可以看到 limx=0 不存在。具体地说, 我们无法在 x=0 周围找到符合限制定义的开放间隔。因此, 该函数在 x=0 时不是连续的。但我们注意到, 当我们从右手边接近 x=0 时, 我们可以看到连续的值趋向于 x=0 。

Review
::回顾

Generate the graph of $\begin{align*}f(x)=\frac{(|x+1|)}{(x+1)}\end{align*}$ using your calculator and discuss the continuity of the function.
::使用您的计算器生成 f( x) = (x+1) (x+1) (x+1) 的图形, 并讨论函数的连续性。

Generate the graph of $\begin{align*}f(x)=\frac{(3x-6)}{(x^2-4)}\end{align*}$ using your calculator and discuss the continuity of the function.
::使用您的计算器生成 f( x) =( 3x- 6)( x2- 4) 的图形, 并讨论函数的连续性。

Is the function $\begin{align*}f(x)=|x-3|\end{align*}$ continuous at $\begin{align*}x=3\end{align*}$ ?
::函数 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x=3 的连续性吗 ?

Is the function $\begin{align*}f(x)=\frac{6x-1}{4x^2+20x+25}\end{align*}$ continuous at $\begin{align*}x=-\frac{5}{2}\end{align*}$ ?
::函数 f( x) =6x- 14x2+20x+25 在 x @ 52 连续吗 ?

Is the function $\begin{align*}f(x)=\frac{3x^2-13x-10}{x^3-4x^2-2x-15}\end{align*}$ continuous at $\begin{align*}x=5\end{align*}$ ?
::函数 f( x) = 3x2- 13x- 10x3- 4x2- 2x- 15 在 x= 5 时连续吗 ?

Find a value of $\begin{align*}k\end{align*}$ which makes the following function continuous: $\begin{align*}f(x) = \begin{cases} x^2+2x+k, \ x \le -1 \\ -x-4, \ \quad \quad x>-1 \end{cases}\end{align*}$
::查找使以下函数连续函数的 k 值 : f( x)\\\ x2+2x+k, x\\\ x- x-4, x1

For the function $\begin{align*}f(x)=\begin{Bmatrix} \sqrt{1-x}, \ x<-3 \\ \frac{4}{3}x+6, \ -3 < x \le 3 \\ x^2, \ x>3\end{Bmatrix}\end{align*}$ classify the discontinuities at

$\begin{align*}x=-3\end{align*}$ and
::x% 3 和

$\begin{align*}x=3\end{align*}$ .
::x=3 = 3 。

::函数 f( x)\% 1 - x, x\\ 343x+6, - 3 < x=3x2, x>3} 将不连续程度分类为 x\\% 3 和 x=3 。

For the function $\begin{align*}f(x)=\frac{3x^3-x^2-27x+9}{3x^2+2x-1}\end{align*}$ classify the discontinuities at

$\begin{align*}x=-1\end{align*}$ and
::x1 和

$\begin{align*}x=\frac{1}{3}\end{align*}$ .
::十分十三秒

::函数 f( x) = 3x3 - x2 - 27x+93x2+2x-1 将不连续状态分类为 x1 和 x=13 。

On what intervals is $\begin{align*}f(x)=\frac{(x^2-1)(4x+1)}{x(x^2+1)(4x+1)}\end{align*}$ continuous?
::F( x) =( x2 - 1) (4x+1) x( x2+1) (4x+1) 持续多久间隔?

On what intervals is $\begin{align*}f(x)=\frac{2}{x-3}+3\end{align*}$ continuous?
::F( x) = 2x-3+3 连续的间隔是多少 ?

On what interval is $\begin{align*}f(x)=\cot^2 (x)\end{align*}$ continuous?
::f( x) =cot2( x) 持续时间间隔是多少 ?

True or False: $\begin{align*}f(x)=\frac{\cos x}{x \sqrt{x-1} (2x-1)}\end{align*}$ is continuous on the interval [0, 1].
::真实或假: f(x) =cosxxxxxxx- 1(2x-1) 在间隔 [0, 1] 上是连续的。

True or False: $\begin{align*}f(x)=\frac{\sin (x)}{\sin (3x)}\end{align*}$ is continuous on the interval $\begin{align*}\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\end{align*}$ .
::True 或 false: f( x) =sin( x) sin( 3x) 在间隔 [%4, %2] 上是连续的。

On what intervals is $\begin{align*}f(x)=\sqrt{x^2-4x+2}\end{align*}$ continuous?
::F(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\x持续??

On what intervals is $\begin{align*}f(x)=\sqrt{x^2+4x+5}\end{align*}$ continuous?
::f(x)\\\\\\\\\ x2+4x+5的间隔是连续的?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

a 职能的连续性

Continuity ::连续连续性

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)

Continuity
::连续连续性

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Review
::回顾

Review (Answers)
::回顾(答复)