Course: 2.10 连续函数的属性

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

连续函数属性

In the previous concept, the was presented intuitively through the imagery of using a pencil to draw a graph on a piece of paper (over a certain interval of the domain) and never lifting the pencil off the paper. As long as the pencil is not lifted off the paper, the graph can be considered to be continuous over that drawing interval. This is certainly not a rigorous description of continuity, but given this analogy, what expectations might you have about arithmetic operations on two functions that are both continuous over a common interval; or the existence of minima and maxima of a continuous function; or the existence of intermediate values between two function values?
::在前一个概念中, 直观地展示了这个图象, 即用铅笔绘制纸块上的图表( 超过某一间距的域) , 并且从不将铅笔从纸上拔掉。只要铅笔不从纸上摘除, 就可以认为这个图图在画间距内是连续的。这当然不是对连续性的严格描述, 但是根据这个类比, 您对两个功能的算术操作有什么期望, 这两个功能在同一个间距内是连续的; 或存在一个连续函数的微量值和峰值; 或两个函数之间的中间值?

Properties of Continuous Functions
::连续函数属性

The previous concept identified the characteristics of a function that is continuous at a point, and over an interval. Let’s explore Given two functions $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ that are continuous over a closed interval $\begin{aligned} [a, b] \end{aligned}$ , would you expect that arithmetic operations on these two functions would also yield functions continuous over $\begin{aligned} [a, b] \end{aligned}$ ?
::先前的概念确定了一个函数的特性,该函数在某个点上和间隔内是连续的。让我们来探索两个函数f(x)和g(x)在封闭的间隔内是连续的,[a,b],你是否期望这两个函数的算术操作也会在[a,b]产生连续的功能?

Given the functions $\begin{aligned} f (x) = x + 3 \end{aligned}$ and $\begin{aligned} g (x) = - x + 0.5 \end{aligned}$ in the closed interval $\begin{aligned} [- 1, 1] \end{aligned}$ , determine if $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are continuous in the interval.
::根据闭合间隔[-1,1] 中的 f(x) =x+3 和 g(x) =x+0.5 函数,确定 f(x) 和 g(x) 在间隔中是否连续。

The functions $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are shown in the graph. Inspection of each function graph and its equation, shows that they are each defined over the closed interval and the function limit at each point in the interval equals the function value at the point. Both functions are continuous in the interval.
::函数 f( x) 和 g( x) 在图形中显示。检查每个函数图形及其方程式, 显示它们都是在封闭间隔内定义的, 间隔内每个点的函数限制等于点的函数值。两者在间隔内都是连续的。

Using the same functions and interval as above, determine if $\begin{aligned} h (x) = f (x) + g (x) \end{aligned}$ is continuous in the interval.
::使用与上述相同的函数和间隔,确定h(x)=f(x)+g(x)在间隔内是否连续。

The sum of the two functions is given by $\begin{aligned} h (x) = 3.5 \end{aligned}$ , and is shown in the figure. The sum function, a constant, is defined over the closed interval and the function limit at each point in the interval equals the constant function value at each point. The sum function is continuous in the interval.
::两个函数的总和由 h( x) = 3. 5 给定,并在图中显示。总函数,即常数,在封闭间隔内定义,在间隔内每个点的函数限制等于每个点的常数函数值。总函数在间隔内是连续的。

Still using the interval and functions as above, determine if $\begin{aligned} h (x) = f (x) g (x) \end{aligned}$ is continuous in the interval.
::仍然使用上面的间隔和函数, 确定 h( x) =f( x) g( x) 在间隔中是否连续。

The product of the two functions is given by $\begin{aligned} h (x) = (x + 3) (- x + 0.5) = - x^{2} + 2.5 x - 1.5 \end{aligned}$ , and is shown in the figure. The product function, a parabola , is defined over the closed interval and the function limit at each point in the interval equals the product function value at each point. The product function is continuous in the interval.
::h(x) = (x+3)(-x+0.5) =x2+2.5x-1.5) 给定了这两个函数的产物,并在图中显示。产品函数,即抛物线,在封闭间隔内定义,在间隔内每个点的函数限制等于每个点的产物函数值。产品函数在间隔内是连续的。

What about the quotient of two continuous functions?
::两个连续函数的商数呢?

Given the functions $\begin{aligned} f (x) = x + 3 \end{aligned}$ and $\begin{aligned} g (x) = - x + 0.5 \end{aligned}$ in the closed interval $\begin{aligned} [- 1, 1] \end{aligned}$ , determine if $\begin{aligned} \frac{f (x)}{g (x)} \end{aligned}$ is continuous in the interval.
::根据闭合间隔[-1,1] 中的 f(x) =x+3 和 g(x) =x+0.5 函数,确定 f(x) g(x) 在间隔中是否连续。

The quotient of the two functions is given by $\begin{aligned} h (x) = \frac{x + 3}{- x + 0.5} \end{aligned}$ , and is shown in the figure.
::这两个函数的商数由 h(x) =x+3-x+0.5给出,并在图中显示。

In the closed interval $\begin{aligned} [- 1, 1] \end{aligned}$ , $\begin{aligned} x = 0.5 \end{aligned}$ is the only place where the function $\begin{aligned} h (x) \end{aligned}$ is undefined, and $\begin{aligned} lim_{x \to 0.5} h (x) \end{aligned}$ does not exist . The function $\begin{aligned} h (x) \end{aligned}$ is not continuous at $\begin{aligned} x = 0.5 \end{aligned}$ , or in the closed interval.
::在闭合间隔 [-1,1] 中,x=0.5是函数 h(x) 唯一没有定义,而 limx=0.5h(x) 不存在的地方。函数 h(x) 在 x=0.5 或闭合间隔时不连续。

The findings in the above simple functions can be generalized in the following properties.
::上述简单职能中的调查结果可归纳为下列财产。

If $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are continuous at any real value $\begin{aligned} c \end{aligned}$ over the closed interval $\begin{aligned} [a, b] \end{aligned}$ , then the following are also continuous at any real value $\begin{aligned} c \end{aligned}$ over the closed interval $\begin{aligned} [a, b] \end{aligned}$ :
::如果f(x)和g(x)在封闭间隔[a,b]上以任何实际值c连续计算,则以下数值在封闭间隔[a,b]上以任何实际值c连续计算,则以下数值在封闭间隔[a,b]上以任何实际值c连续计算:

$\begin{aligned} f (x) + g (x) \end{aligned}$
:fx)+g(x)

$\begin{aligned} f (x) - g (x) \end{aligned}$
:fx)-g(x)

$\begin{aligned} f (x) g (x) \end{aligned}$
:fx)g(x)

$\begin{aligned} \frac{f (x)}{g (x)} \end{aligned}$ , as long as $\begin{aligned} g (c) \neq 0 \end{aligned}$ .
:x)g(x)x,只要g(c)%0。

and the Extreme Value (Min-Max) Theorem are two other properties of a function that is continuous over a closed interval.
::和极端值(Min-Max)定理是连续在封闭间隔内连续的函数的另外两个属性。

The Intermediate Value Theorem and Extreme Value Theorem
::中间价值理论和极端价值理论

The Intermediate Value Theorem states that i f a function is continuous on a closed interval $\begin{aligned} [a, b] \end{aligned}$ , then the function assumes every value between $\begin{aligned} f (a) \end{aligned}$ and $\begin{aligned} f (b) \end{aligned}$ .
::《中间值理论》规定,如果一个函数在封闭间隔[a,b] 连续,则该函数承担f(a)和f(b)之间的每一个数值。

The Intermediate Value Theorem can be used to analyze and approximate zeros of functions.
::中间值定理可用于分析和大致为零的职能。

Use the Intermediate Value Function to show that there is at least one zero of the function $\begin{aligned} f (x) = 3 x^{4} - 3 x^{3} - 2 x + 1 \end{aligned}$ in the indicated interval $\begin{aligned} [1, 2] \end{aligned}$ .
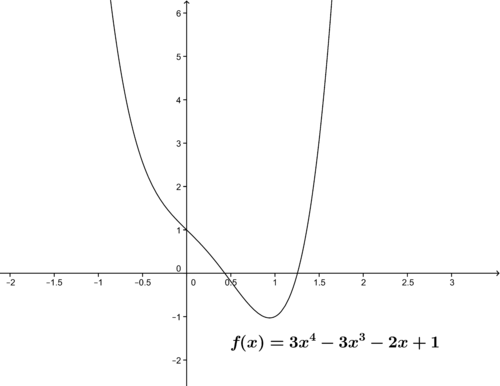
::使用中间值函数来显示,在指定的间隔[1,2] 中,函数 f(x)=3x4-3x3-3x3-2x+1至少有一个零。

The graph of this function, shown below, is shaped somewhat like a parabola, and is continuous in the interval.
::此函数的图示如下所示,形状有点像抛物线,在间隔内连续存在。

In order to apply the Intermediate Value Theorem, we need to find a pair of $\begin{aligned} x \end{aligned}$ - values that have function values with different signs. A few values are shown in the table below.
::为了应用中间值理论,我们需要找到一对带有不同符号的函数值的X值。下面的表格中列出了几个数值。

*$\begin{aligned} x \end{aligned}$* ::x x	1.1	1.2	1.3
*$\begin{aligned} f (x) \end{aligned}$* :fx)	-0.80	-0.36	0.37

We see that the sign of the function values changes from negative to positive somewhere between 1.2 and 1.3. Hence, by the Intermediate Value theorem, there is some value $\begin{aligned} c \end{aligned}$ in the interval (1.2, 1.3) such that $\begin{aligned} f (c) = 0 \end{aligned}$ .
::我们看到函数值的符号从负值变为正值,介于1.2和1.3之间。因此,根据中间值定理,在间隔(1.2、1.3)中,有一定的c值,例如f(c)=0。

The Extreme Value (Min-Max Theorem) is a consequence of the Intermediate Value Theorem.
::极值(Min-Max理论)是中间值理论的结果。

The Extreme Value (Min-Max) Theorem states that i f a function $\begin{aligned} f (x) \end{aligned}$ is continuous in a closed interval $\begin{aligned} I \end{aligned}$ , then $\begin{aligned} f (x) \end{aligned}$ has both a maximum value and a minimum value in $\begin{aligned} I \end{aligned}$ .
::极端值( Min-Max) 理论称,如果函数f(x) 在闭合间隔I 中连续,那么f(x) 具有最大值和最小值I。

Examples
::实例

Example 1
::例1

Earlier, you were asked about your expectations for the continuity of functions formed by arithmetic operations on two continuous functions. The conclusion of this section is that, except for the quotient of functions, arithmetic operations on two functions that are continuous at a point or in an interval yield a new function that is continuous at the point or in the interval. With the quotient of two functions, the concern is always to identify where the denominator is 0; at this location the quotient function is not continuous.
::早些时候,有人询问您对两个连续函数的算术操作所形成的功能的连续性的期望。本节的结论如下:除了函数的商数外,两个函数的算术操作在一个点或一个间隔内连续进行,产生一个在点或间隔内连续进行的新函数。在两个函数的商数上,关注的始终是确定分母是0的位置;在此位置,商数函数不是连续的。

Example 2
::例2

Consider $\begin{aligned} f (x) = x^{3} + 1 \end{aligned}$ and interval $\begin{aligned} I = [- 2, 2] \end{aligned}$ . Determine minimum and maximum values.
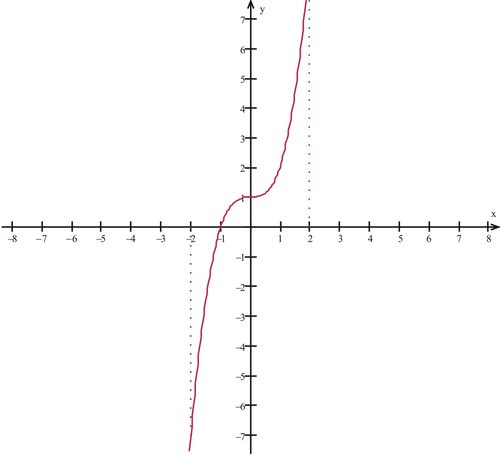
::考虑 f(x) =x3+1 和间隔 I = [-2,2] 。确定最小值和最大值。

Since the function is continuous on the closed interval $\begin{aligned} I \end{aligned}$ , this function has a minimum and a maximum on the interval. The function graph shows that at $\begin{aligned} x = - 2 \end{aligned}$ the function has a minimum value $\begin{aligned} f (- 2) = - 7 \end{aligned}$ ; and at $\begin{aligned} x = 2 \end{aligned}$ , a maximum value $\begin{aligned} f (2) = 9 \end{aligned}$ .
::由于该函数在关闭间隔 I 上是连续的, 此函数在间隔上有最小值和最大值。函数图显示, 在 x2 时, 该函数有最小值 f(-2)\\\\ 7; 在 x=2 时, 最大值 f(2)=9 。

Review
::回顾

For #1-5, explain how you know that the function has a root in the given interval. (Hint: Use the Intermediate Value Function to show that there is at least one zero of the function in the indicated interval.):
::对于 # 1 5, 请解释您如何知道该函数在给定间隔内有一个根。 (提示: 使用中间值函数来显示在指定的间隔内该函数至少为0 :

$\begin{aligned} f (x) = x^{3} + 2 x^{2} - x + 1 \end{aligned}$ , in the interval [-3,-2].
::f(x) =x3+2x2-x+1, 间隔 [3-2] 。

$\begin{aligned} f (x) = \sqrt{x} - \sqrt[3]{x} - 1 \end{aligned}$ , in the interval [9,10].
::f(x)=x-x3-1,间隔[9,10]。

$\begin{aligned} f (x) = x^{2} + x - 2 \end{aligned}$ , in the interval [-3,0].
::f(x) =x2+x-2, 间隔[ 30] 。

$\begin{aligned} f (x) = \frac{4 x^{2} - 1}{x^{2} + 3 x + 2} \end{aligned}$ , in the interval [-1,0].
::f(x) = 4x2- 1x2+3x+2, 间隔 [-0] 。

$\begin{aligned} f (x) = \frac{2}{x + 3} - 4 \end{aligned}$ , in the interval [-3,0].
::f(x) = 2x+3-4, 间隔[ 30] 。

True or False: $\begin{aligned} f (x) = \sin (x) + \cos (x) \end{aligned}$ has a root on the interval $\begin{aligned} [0, π] \end{aligned}$ .
::True 或 false: f( x) =sin( x) +cos( x) 在间隔 [ 0. 上有一个根。

True or False: By the Intermediate Value Theorem $\begin{aligned} f (x) = \sin (x) + c o s^{2} (x) \end{aligned}$ has no root on the interval $\begin{aligned} [0, π] \end{aligned}$ since $\begin{aligned} f (0) = f (π) = 1 \end{aligned}$ .
::真实或假 : 根据中间值参数 f(x) =sin(x) +cos2(x) 在间隔 [0] 上没有根 , 因为 f(0) =f(x) = 1 。

True or False: $\begin{aligned} f (x) = \frac{x^{2} + 1}{\cos (x)} \end{aligned}$ has a root on the interval $\begin{aligned} [0, π] \end{aligned}$ .
::True 或 false: f( x) =x2+1cos @% (x) 在间隔 [0] 上有一个根。

On which interval is $\begin{aligned} f (x) = x - \sin (x) + 1 \end{aligned}$ guaranteed by the IVT to have a root?
1. $\begin{aligned} [0, \frac{2 π}{3}] \end{aligned}$
2. $\begin{aligned} [- \frac{π}{3}, \frac{π}{3}] \end{aligned}$
3. $\begin{aligned} [- \frac{2 π}{3}, 0] \end{aligned}$
4. $\begin{aligned} [- π, π] \end{aligned}$
::F(x) =x-sin(x)+1 受IVT 保证具有根的间隔? [0,23] [3,3] [-23,0] [1,]

Find an interval on which $\begin{aligned} f (x) = e^{x} + x \end{aligned}$ has a root.
::查找 f( x) =ex+x 有根的间隔。

Find intervals on which $\begin{aligned} f (x) = x^{3} + 5 x^{2} - 4 x - 20 \end{aligned}$ has a root.
::查找 f( x) =x3+5x2 - 4x - 20 有根的间隔。

For #12-15, use the Extreme Value Theorem to determine whether the given statement is true or false.
::对于第12-15号,使用极端价值理论来确定特定声明是真实的还是虚假的。

The Extreme Value Theorem guarantees that the function $\begin{aligned} \sqrt{| \sin (x^{3}) |} \end{aligned}$ has a minimum value on the interval [-3, 3].
::极端值理论保证函数 sin(x3)在间隔[-3,3] 上具有最小值。

The Extreme Value Theorem guarantees that the function $\begin{aligned} (x - 1)^{3} \end{aligned}$ has a maximum value on the interval [1, 3].
::极端值理论保证函数(x-1) 3 在间隔[1, 3] 上具有最大值。

The Extreme Value Theorem guarantees that the function $\begin{aligned} x^{2} + 3 x + 2 \end{aligned}$ has a minimum value on the interval [-3, 0].
::极端值理论保证函数x2+3x+2在间隔[3,0]上具有最小值。

The Extreme Value Theorem guarantees that the function $\begin{aligned} \frac{4 x}{x^{2} + 3 x + 2} \end{aligned}$ has a minimum value on the interval [-3, 0].
::极端值理论保证函数 4x22+3x+2 在间隔[3,0] 上具有最小值。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

连续函数属性

Properties of Continuous Functions ::连续函数属性

The Intermediate Value Theorem and Extreme Value Theorem ::中间价值理论和极端价值理论

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Review ::回顾

Review (Answers) ::回顾(答复)