Course: 4.1 相关利率 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 相关利率

Collapse Expand
相关利率
In the concept on , you learned that given a relationship between two quantities, the relationship between their respective rates of change can be determined. This is often an invaluable tool in applications, since it allows us to find the rate at which some quantity is changing by relating it to other quantities whose rates of change are known (or at least more easily found). For example, if you were at the scene of an accident where an oil spill from a large tanker is spreading in a circular pattern whose radius you determine is increasing by about 1 ft per second, would you be able to tell someone how fast the oil spill area was increasing when the radius was about 30 feet?
::在这一概念中,你了解到,鉴于两个数量之间的关系,可以确定它们各自的变化率之间的关系。这往往是一个非常宝贵的应用工具,因为它使我们能够通过将某些数量的变化速度与已知(或至少更容易找到)变化率的其他数量联系起来,从而发现某些数量的变化速度。比如,如果你身处一个事故现场,当时大油轮的漏油正在以圆形模式扩散,而你确定其半径每秒增加约1英尺,你能否告诉某人,当半径大约为30英尺时,石油溢漏区正在增加多快?

Related Rates
::相关利率

What do we mean by related rates? These are simply the , rates, of one or more parameters that are related to each other through an equation. The relationship between the rates is obtained by taking the derivative of some other relationship between the parameters.
::相关税率意味着什么?这些仅仅是通过等式相互联系的一个或多个参数的、率、率、或多个参数。比率之间的关系是通过从参数之间的某种其他关系中衍生出来的。

A simple example with a familiar geometric shape should help illustrate the concept.
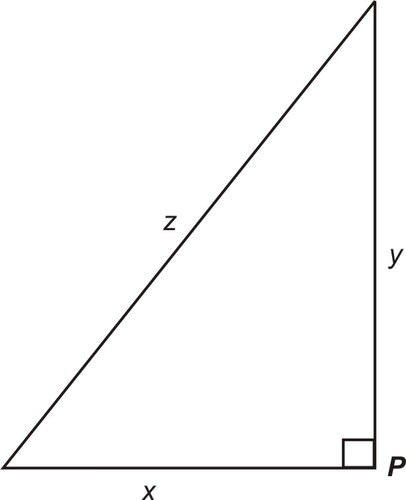
::一个具有熟悉几何形状的简单例子应有助于说明这一概念。

Consider the simple right triangle in the figure below with sides $\begin{aligned} x, y, \end{aligned}$ and $\begin{aligned} z \end{aligned}$ . The relationship between the sides is governed by the Pythagorean Theorem.
::考虑下图中带有侧面 x、y 和 z 的简单右三角形。双方之间的关系由毕达哥伦理论管辖。

$\begin{aligned} x^{2} + y^{2} = z^{2} \end{aligned}$

::x2+y2=z2

We could easily attach some real-life situation to this geometric figure. Say for instance that $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ represent the paths of two people starting at point $\begin{aligned} p \end{aligned}$ and walking North and West, respectively, for two hours. The quantity $\begin{aligned} z \end{aligned}$ represents the distance between them at any time $\begin{aligned} t \end{aligned}$ . Let’s now determine any relationships between the various rates of change that we get by implicitly differentiating the original equation $\begin{aligned} x^{2} + y^{2} = z^{2} \end{aligned}$ with respect to time $\begin{aligned} t \end{aligned}$ .
::我们可以很容易地将一些真实情况附于这个几何图中。比如说, x 和 y 分别代表从p点开始的两个人的行走路径,然后在北面和西面行走两个小时。数量 z 代表他们在任何时候的距离。现在让我们来决定我们通过隐含地区分原始方程式 x2+y2=z2 相对于时间 t 所得到的各种变化率之间的关系。

$\begin{aligned} \frac{d}{d t} [x^{2} + y^{2}] & = \frac{d}{d t} [z^{2}] \\ 2 x \frac{d x}{d t} + 2 y \frac{d y}{d t} & = 2 z \frac{d z}{d t} \\ x \frac{d x}{d t} + y \frac{d y}{d t} & = z \frac{d z}{d t} \dots Equation 1 \end{aligned}$

::ddt[x2+y2]=ddt[z2,2xdxdt+2ydydt=2zdzddddt+ydydt=zdzdt=zdzdt...等式 1

Implicit differentiation of the Pythagorean relationship between the side lengths has yielded relationships between the side length derivatives, and since the derivatives are rates, this is an example of related rates .
::Pythagorean人关系在副长之间的隐性区别已导致副长衍生物之间的关系,由于衍生物是利率,这是相关利率的一个实例。

How might the relationship above be used to solve or answer a problem?
::如何利用上述关系解决或解决一个问题?

Let’s say that person is walking in the $\begin{aligned} x \end{aligned}$ -direction at 5 mph, and that another person is walking in the $\begin{aligned} y \end{aligned}$ -direction at 3 mph. The distance, $\begin{aligned} z \end{aligned}$ , between the walkers is changing with time, and the time rate of change of, $\begin{aligned} z, \frac{d z}{d t}, \end{aligned}$ is dependent on the rates at which the two people are walking.
::换句话说,这个人在5mph的X方向行走,另一个人在3mph的Y方向行走。行尸之间的距离,Z,随时间而变化,Z,dzdt的改变速度取决于两人行走的速度。

One problem that we could pose is:
::我们可以提出的一个问题是:

At what rate is the distance between $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ increasing after one hour? That is, what is $\begin{aligned} \frac{d z}{d t} \end{aligned}$ after one hour?
::一小时后 x 和 y 之间的距离增加多少? 一小时后 dzdt 是什么 ?

Assume that they have walked for one hour. So $\begin{aligned} x = 5 m i \end{aligned}$ and $\begin{aligned} y = 3 \end{aligned}$ .
::假设他们步行了一个小时。所以 x=5 mi and y= 3 。

Using the Pythagorean Theorem, we find the distance between them after one hour is $\begin{aligned} z = \sqrt{34} = 5.83 m i l e s \end{aligned}$ .
::利用毕达哥里安神话我们发现它们之间的距离一个小时后是z=34=5.83英里

If we substitute the values for $\begin{aligned} x, y, \end{aligned}$ and $\begin{aligned} z \end{aligned}$ into Equation 1 along with the individual rates we get
::如果我们将x、y和z的值与我们得到的个别利率同以x、y和z等值取代,

$\begin{aligned} 5 (5) + 3 (3) & = \sqrt{34} \frac{d z}{d t} \\ 34 & = \sqrt{34} \frac{d z}{d t} \\ \frac{34}{\sqrt{34}} & = \frac{d z}{d t} . \end{aligned}$

::5(5)+3(3)=34dzdt34=34dzdt3434=dzdt。

Hence after one hour the distance between the two people is increasing at a rate of:
::因此,一个小时后,两人之间的距离以下列速度增加:

$\begin{aligned} \frac{d z}{d t} = \frac{34}{\sqrt{34}} \approx 5.83 m p h \end{aligned}$ .
::dzdt=3434 5.83 mph.

Suppose we have a rectangular field and we know that at an instant of time, the length is changing at the rate of 8 ft/hour and the perimeter is changing at a rate of 24 ft/hour. At what rate is the width changing at that instant? At what rate is the area changing at that instant?
::假设我们有一个矩形场,我们知道在某一时刻,长度以每小时8英尺的速度变化,周边以每小时24英尺的速度变化。当时刻宽度以什么速度变化?当时,面积以什么速度变化?

You are familiar with the formulas for Perimeter:
::您熟悉周边的公式 :

$\begin{aligned} P = 2 l + 2 w \end{aligned}$
::P=2l+2w

If we differentiate the perimeter equation, we have
::如果我们区分了周边方程

Equation 2: $\begin{aligned} \frac{d P}{d t} = 2 \frac{d l}{d t} + 2 \frac{d w}{d t} \end{aligned}$ .
::等式 2:dPdt=2ddt+2ddwdt。

Substituting our known information into Equation 2, we have
::将已知信息转换为2号等号

$\begin{aligned} 24 & = (2 \times 8) + 2 \times \frac{d w}{d t} \\ 8 & = 2 \times \frac{d w}{d t} \\ 4 & = \frac{d w}{d t} . \end{aligned}$

::24=(2x8)+2xdwdt8=2xdwdt4=dwdt。

The width is changing at a rate of 4 ft/hr.
::宽度以每小时4英尺的速度变化。

Examples
::实例

Example 1
::例1

Earlier, you were asked about being at the scene of an accident where an oil spill from a large tanker is spreading in a circular pattern whose radius you determine is increasing by about 1 ft per second. Would you be able to tell someone how fast the oil spill area was increasing when the radius was about 30 feet?
::早些时候,有人问您是否身处一个事故现场,在那里,大型油轮的漏油事件正在以环状模式扩散,您确定其半径每秒增加约1英尺。您能否告诉某人,当半径约30英尺时,漏油区增速有多快?

Since the circular area of the spill is $\begin{aligned} A = π r^{2} \end{aligned}$ , the time rate of change of the area is $\begin{aligned} \frac{d A}{d t} = π 2 r \frac{d r}{d t} \end{aligned}$ . This means that with $\begin{aligned} \frac{d r}{d t} = 1 f t / s e c \end{aligned}$ , when $\begin{aligned} r = 30 f t, \frac{d A}{d t} = 60 π f t^{2} / s e c \end{aligned}$ .
::由于溢漏的圆环区域为Ar2, 区域变化的时间速率为 dAdt2rdd。这意味着, drdt=1 ft/sec, 当 r= 30 ft, dAdt= 60ft2/sec 时。

Example 2
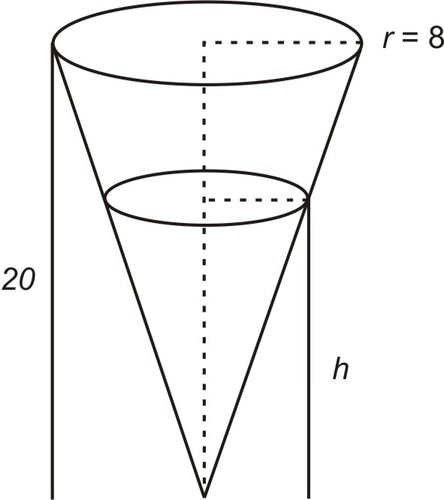
::例2

We have a water tank shaped as an inverted right circular cone. Suppose that water flows into the tank at the rate of $\begin{aligned} 5 f t^{3} / m i n \end{aligned}$ . At what rate is the water level rising when the height of the water in the tank is 6 feet?
::假设水以5立方厘米/分钟的速度流入水箱。当水箱的水高度为6英尺时,水位上升的速度是多少?

We know that the volume of water in the water tank is:
::我们知道水箱的水量是:

$\begin{aligned} V = \frac{1}{3} π r^{2} h \end{aligned}$
::V=13°r2h

When we differentiate this equation we get:
::当我们区分这个等式时,我们得到的是:

(2r)%20%5Cfrac%7Bdr%7D%7Bdt%7D%2B%5Cfrac%7B1%7D%7B3%7D%20%5Cpi%20r%5E2%20%5Cfrac%7Bdh%7D%7Bdt%7D"> $\begin{aligned} \frac{d V}{d t} = \frac{1}{3} π (h) (2 r) \frac{d r}{d t} + \frac{1}{3} π r^{2} \frac{d h}{d t} \end{aligned}$ .
::dVdt=13(2r)ddt+13r2dhdt。

This is a related rates equation. The rate $\begin{aligned} \frac{d V}{d t} \end{aligned}$ is related to the rates $\begin{aligned} \frac{d r}{d t} \end{aligned}$ and $\begin{aligned} \frac{d h}{d t} \end{aligned}$ .
::这是相关的费率方程式。 dVdt 的费率与 drdt 和 dhdt 的费率有关。

We know $\begin{aligned} \frac{d V}{d t} = 5 f t^{3} / m i n \end{aligned}$ , do no know $\begin{aligned} \frac{d r}{d t} \end{aligned}$ , but want to find $\begin{aligned} \frac{d h}{d t} \end{aligned}$ . We need to somehow find a relationship between $\begin{aligned} h \end{aligned}$ and $\begin{aligned} r \end{aligned}$ .
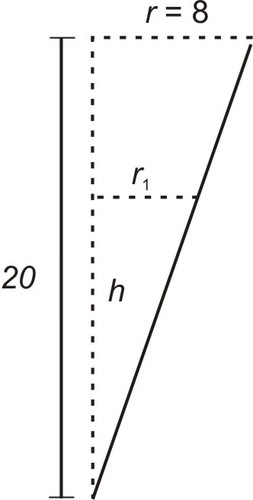
::我们知道 dVdt=5 ft3/min, 不知道 drdt, 但是想要找到 dhdt。我们需要找到h和r之间的关系。

Let $\begin{aligned} r_{1} \end{aligned}$ be the radius of the surface of the water as it flows out of the tank.
::让 r1 成为水流出罐体时水面的半径。

Note that the two triangles are similar and thus corresponding parts are proportional. In particular,
::请注意,这两个三角形是相似的,因此相应的部分是成比例的。

$\begin{aligned} \frac{r_{1}}{h} & = \frac{8}{20} \\ r_{1} & = \frac{8 h}{20} = \frac{2 h}{5} . \end{aligned}$

::r1h=820r1=8h20=2h5。

We can write this as a general relationship between $\begin{aligned} r \end{aligned}$ and $\begin{aligned} h \end{aligned}$ .
::我们可以把它写成r和h之间的一般关系

$\begin{aligned} r = \frac{2 h}{5} \end{aligned}$ , which means also that $\begin{aligned} \frac{d r}{d t} = \frac{2}{5} \frac{d h}{d t} \end{aligned}$ . We have the relationships we need.
::r=2h5,也就是说drdt=25dhdt。我们有我们需要的关系。

Now we can solve the problem in a couple of ways: (a) substitute $\begin{aligned} r = (\frac{2 h}{5}) \end{aligned}$ into the original equation for $\begin{aligned} V \end{aligned}$ , or (b) substitute $\begin{aligned} r = (\frac{2 h}{5}) \end{aligned}$ and $\begin{aligned} \frac{d r}{d t} = \frac{2}{5} \frac{d h}{d t} \end{aligned}$ into the equation for $\begin{aligned} \frac{d V}{d t} \end{aligned}$ . Let’s try approach (a).
::现在我们可以用几种方式解决问题a) 将r= (2h5) 替换成V 的原始方程,或(b) 替换r= (2h5) 和 drdt= 25dhdt 。让我们尝试(a) 。

$\begin{aligned} V = \frac{1}{3} π {(\frac{2 h}{5})}^{2} h = \frac{4 π}{75} h^{3} \end{aligned}$

::V=13-( 2h5) 2h=4-75h3

Hence $\begin{aligned} \frac{d V}{d t} = \frac{12 π}{75} h^{2} \frac{d h}{d t} \end{aligned}$ , and by substitution,
::因此,dVdt=1275h2dhdt,通过替代,

$\begin{aligned} 5 & = \frac{12 π}{75} (36) \frac{d h}{d t} \\ \frac{d h}{d t} & = \frac{375}{432 π} \approx 0.28 \frac{f t}{m i n} . \end{aligned}$

::5=1275(36)dhdddhdt=3754320.28ftmin。

Review
::回顾

Make up a related rates problem about the area of a rectangle. Illustrate the solution to your problem.
::在矩形区域形成一个相关的利率问题。提示解决您问题的方法。

Suppose that a particle is moving along the curve $\begin{aligned} 4 x^{2} + 16 y^{2} = 32 \end{aligned}$ . When it reaches the point (2, 1), the $\begin{aligned} x \end{aligned}$ -coordinate is increasing at a rate of 3 ft/sec. At what rate is the $\begin{aligned} y \end{aligned}$ -coordinate changing at that instant?
::假设一个粒子正在沿着曲线 4x2+16y2=32 移动。当它到达点 (2, 1) 时, x 坐标正在以 3 ft/sec 的速率递增。 y 坐标在那一瞬间变化的速率是多少 ?

A regulation softball diamond is a square with each side of length 60 ft. Suppose a player is running from first base to second base at a speed of 18 ft/sec. At what rate is the distance between the runner and home plate changing when the runner is $\begin{aligned} \frac{2}{3} \end{aligned}$ of the way from first to second base?
::调制软球钻石是方形,每边长度为60英尺。假设玩家从一垒跑到二垒, 速度为18英尺/秒。当跑者从一垒跑到二垒时, 跑者与家用板之间的距离会以什么速度变化? 当跑者从一垒跑到二垒时, 跑者从23英尺跑到二垒时, 跑者与家用板之间的距离会以什么速度变化 ?

At a recent Hot Air Balloon festival, a hot air balloon was released. Upon reaching a height of 300 ft, it was rising at a rate of 20 ft/sec. Mr. Smith was 100 ft away from the launch site watching the balloon. At what rate was the distance between Mr. Smith and the balloon changing at that instant?
::在最近的热空气气球节上,热空气气球被释放,达到300英尺高度,以20英尺/秒的速度上升,史密斯先生离发射场100英尺远,观看气球,史密斯先生与气球瞬间变化之间的距离是多少?

Two trains left the St. Louis train station in the late morning. The first train was traveling East at a constant speed of 65 mph. The second train traveled South at a constant speed of 75 mph. At 3 PM, the first train had traveled a distance of 120 miles while the second train had traveled a distance of 130 miles. How fast was the distance between the two trains changing at that time?
::两列火车于上午晚些时候离开圣路易斯火车站。第一列火车以65英里的固定速度向东行驶。第二列火车以75英里的固定速度向南行驶。在下午3时,第一列火车行驶120英里,第二列火车行驶130英里。当时两列火车之间的距离变化有多快?

Suppose that a 17 ft ladder is sliding down a wall at a rate of -6 ft/sec. At what rate is the bottom of the ladder moving when the top is 8 ft from the ground?
::假设17英尺梯子以 - 6英尺/ sec 的速率滑下墙壁。当顶部距离地面8英尺时, 梯子底部移动的速率是多少 ?

Suppose that the length of a rectangle is increasing at the rate of 6 ft/min and the width is increasing at a rate of 2 ft/min. At what rate is the area of the rectangle changing when its length is 25 ft and its width is 15 ft?
::假设矩形的长度以 6 英尺/ 分钟的速度增长,宽度以 2 英尺/ 分钟的速度增长。当矩形的长度为 25 英尺,宽度为 15 英尺时, 矩形的面积变化的速率是多少?

Suppose that the quantity demand of new $\begin{aligned} 40^{''} \end{aligned}$ plasma TVs is related to its unit price by the formula $\begin{aligned} p + x^{2} = 1200 \end{aligned}$ , where $\begin{aligned} p \end{aligned}$ is measured in dollars and $\begin{aligned} x \end{aligned}$ is measured in units of one thousand. How is the quantity demand changing when $\begin{aligned} x = 20, p = 1500, \end{aligned}$ and the price per TV is decreasing at a rate of $10?
::假设新的40等离子电视的数量需求与以p+x2=1200公式计算的其单价有关,p以美元计量,x以千计。当 x=20,p=1500时,数量需求变化如何,而每台电视的价格以10美元的速度下降?

The volume of a cube with side $\begin{aligned} s \end{aligned}$ is changing. At a certain instant, the sides of the cube are 6 inches and increasing at the rate of $\begin{aligned} \frac{1}{4} i n / m i n \end{aligned}$ . How fast is the volume of the cube increasing at that time?
::立方体的侧面体积正在变化。立方体的侧面在某一时刻是 6 英寸, 以 14 英寸/ 分钟的速率增长。立方体体体体体积当时增速多快 ?

(1) Suppose that the area of a circle is increasing at a rate of $\begin{aligned} 24 i n^{2} / m i n \end{aligned}$ . How fast is the radius increasing when the area is $\begin{aligned} 36 π i n^{2} \end{aligned}$ ? (2) How fast is the circumference changing at that instant?
:1) 假设圆圈面积以24英寸2/min的速度增长,当面积为36英寸2时半径增加的速度有多快? (2) 环形在这一时刻变化的速度有多快?

The radius of a circle is getting bigger at a rate of 5 centimeters per second. How fast is the area of the circle increasing when the radius is equal to ten centimeters?
::圆的半径正在以每秒5厘米的速度扩大。当圆的半径等于10厘米时,圆的面积会增加多快?

The area of a circle is expanding at a rate of 100 square centimeters a second at an instant when its radius is expanding at a rate of 50 centimeters a second. What is the circle’s radius at that instant?
::当圆的半径以每秒50厘米的速度扩张时,圆的面积正在以每秒100平方厘米的速度扩张。当圆的半径以每秒50厘米的速度扩张时,圆的半径是多少?

At a given instant, the volume of a cylinder with a fixed circular cross sectional area of 6 square centimeters is increasing at a rate of 10 cubic centimeters a second. What is the rate of increase of its height at that instant?
::在某一瞬间,一个圆形圆形横跨面积6平方厘米的圆柱体的体积以每秒10立方厘米的速度增加。当时其高度的增长率是多少?

Express the rate of change of a cylinder’s volume as a function of its radius, its height, and the rate of change of its radius, if its height is assumed to be held constant.
::如果假设圆柱体的高度保持不变,则以圆柱体半径、高度和圆柱体半径变化率的函数表示圆柱体的体积变化率。

A four dimensional object whose momentum is given by the formula $\begin{aligned} M = \sin (π x_{1}) + δ x {_{2}}^{3} + \ln (x_{3} x_{4}) x {_{1}}^{5} \end{aligned}$ , where delta is a constant, is falling into a black hole. The resulting compression causes its $\begin{aligned} x_{1} \end{aligned}$ value to shrink at a rate of 8 million miles a second (while the other variables remain constant.) If $\begin{aligned} x_{3} = \frac{5}{x_{4}} \end{aligned}$ , what is the instantaneous change in its momentum when $\begin{aligned} x_{1} = 1 \end{aligned}$ ?
::M=sin(xx1) x23+ln(x3x4)x15 公式给四维对象带来动力,而公式 M=sin(xx1) x23+ln(x3x4)x15 是三角洲的常数) 正在坠入黑洞。由此产生的压缩导致其 x1 值以每秒800万英里的速度缩缩缩( 而其他变量则保持不变 ) 。如果 x3=5x4, 当 x1=1 时其动力的瞬时变化是什么?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

相关利率

Related Rates ::相关利率

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Review ::回顾

Review (Answers) ::回顾(答复)

Related Rates
::相关利率

Examples
::实例

Example 1
::例1

Example 2
::例2

Review
::回顾

Review (Answers)
::回顾(答复)