4.2 找到功能的Maxima和Minima(外形)

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 查找函数的Maxima 和 Minima( Extrema)

  Collapse Expand

  查找函数的Maxima 和 Minima( Extrema)

  播放段落

  Being able to identify the smallest and largest values of a function (extrema), and where they occur in some interval on the domain or over the entire domain, is useful in graphing a function equation as well as in solving “optimization” problems. The location of these extrema is tied to the behavior of the derivative. You learned in prior work with quadratic functions ( , $\begin{align*}y=ax^2+bx+c\end{align*}$ ), that the least or greatest value of the parabola could be found at the vertex of the parabola (on the axis of symmetry $\begin{align*}x=-\frac{b}{2a}\end{align*}$ ).  How are the derivative of the quadratic function and the vertex $\begin{align*}x=-\frac{b}{2a}\end{align*}$  related?
  ::能够辨别函数(extrema)中最小和最大的值(extrema),以及在域内或整个域内某段间隔内发生的数值,对于绘制函数方程式图和解决“优化”问题有用。这些矩形的位置与衍生物的行为相关联。您在使用二次函数( y=ax2+bx+c) 的先前工作中了解到,在抛物线的顶端( 对称xb2a轴) 中可以找到抛物线的最小或最大值。 二次函数的衍生物和顶端 xb2a 的相关衍生物如何?

  播放段落

  Extrema
  ::极端

  播放段落

  Let’s start our discussion with some formal working definitions of the maximum and minimum values of a function.
  ::让我们先从一个函数最大值和最低值的正式工作定义开始讨论。

  播放段落
  • A function  $\begin{align*}f\end{align*}$ has a maximum at $\begin{align*}x=a\end{align*}$  if $\begin{align*}f(a) \ge f(x)\end{align*}$  for all $\begin{align*}x\end{align*}$  in the domain of $\begin{align*}f\end{align*}$ .
    ::如果 f(a)\f(x) 所有 x 在 f 域中, 函数 f 在 x=a 时最大值为 x 。
  播放段落
  • A function  $\begin{align*}f\end{align*}$ has a minimum at  $\begin{align*}x=a\end{align*}$ if $\begin{align*}f(a) \le f(x)\end{align*}$  for all $\begin{align*}x\end{align*}$  in the domain of $\begin{align*}f\end{align*}$ .
    ::如果 f(a)\f(x) 所有 x 在 f 域内, 函数 f 至少有 x=a 。

  播放段落

  The values of the function for these $\begin{align*}x\end{align*}$ -values are called extreme values or extrema .
  ::这些 x 值的函数值被称为极端值或extrema。

  播放段落

  Here is an example of a function that has a maximum at $\begin{align*}x=a\end{align*}$  and a minimum at $\begin{align*}x=d\end{align*}$ :
  ::以下是一个函数的示例,该函数在 x=a 时具有最大值,在 x=d 时具有最低值:

  

  
  

  播放段落

  Observe the graph at $\begin{align*}x=b\end{align*}$ . While we do not have a minimum at $\begin{align*}x=b\end{align*}$ , we note that $\begin{align*}f(b) \le f(x)\end{align*}$  for all $\begin{align*}x\end{align*}$ near $\begin{align*}b\end{align*}$ . We say that the function has a local minimum at $\begin{align*}x=b\end{align*}$ .
  ::观察 x=b 的图形。 虽然在 x=b 时我们没有最小值, 但我们注意到, f(b)\f(x) 对于所有 x 接近 b 。 我们说, 该函数在 x=b 时具有本地最小值 。

  播放段落

  Similarly, we say that the function has a local maximum at $\begin{align*}x=c\end{align*}$  since $\begin{align*}f(c) \ge f(x)\end{align*}$  for some $\begin{align*}x\end{align*}$  contained in open intervals of $\begin{align*}c\end{align*}$ .
  ::同样,我们说,自f(c)-f(x)以来,该函数在x=c时具有一个本地最大值,因为某些x在c的开放间隔内。

  播放段落

  Remember to use the terms maximum and minimum (without including the term local) only when you are talking about the absolute or global extrema values of the function; local extrema or relative extrema should be called local maximum or local minimum. 
  ::仅当您在谈论函数的绝对值或全球极限值时,才记住使用最大值和最小值(不包括本地术语);本地extrema或相对极限值应称为本地最大值或本地最小值。

  播放段落

  Do all functions have a maximum and minimum? Yes, all continuous functions do. This is stated by the Extreme Value Theorem  that we discussed in the concept on Continuity.
  ::是否所有功能都有最大和最小的功能? 是的, 所有连续的功能都有。 这是由我们在连续性概念中讨论过的“ 极端价值理论” 所表述的 。

  播放段落

  Extreme Value Theorem:  If a function $\begin{align*}f(x)\end{align*}$  is continuous in a closed interval $\begin{align*}I\end{align*}$ , then $\begin{align*}f(x)\end{align*}$  has both a maximum value and a minimum value in $\begin{align*}I\end{align*}$ .
  ::极端值定理:如果函数f(x)在闭合间隔I中连续,则f(x)在I中具有最大值和最低值。

  播放段落

  This makes sense conceptually. Try drawing a function (on a closed interval, including the endpoints) so that no point is at the highest part of the graph. No matter how the function is sketched, there will be at least one point that is highest.
  ::这在概念上是有道理的。尝试绘制函数(闭合间隔,包括终点),这样图形的最高部分就不会有点。无论如何绘制函数,至少都会有一个最高点。

  播放段落

  How do extreme values, maxima and minima, relate to ? The French mathematician Fermat shows how in Fermat's Theorem : If $\begin{align*}f(c)\end{align*}$  is an extreme value of $\begin{align*}f\end{align*}$  for some open interval containing $\begin{align*}c\end{align*}$ , then either $\begin{align*}f^\prime(c)=0\end{align*}$ , or  $\begin{align*}f^\prime(c)\end{align*}$   does not exist .
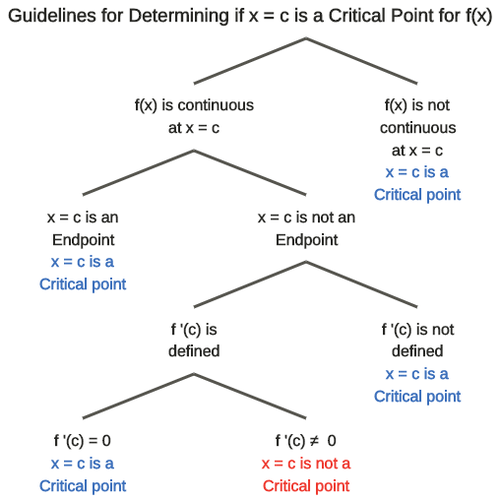
  ::法国数学家费马特(Fermat)的理论显示:如果f(c)是含有c的某种开放间隔的f(f)值的极端值,那么 f*(c)=0或 f*(c)就不存在了。

  播放段落

  This relationship between the location of extrema and the derivative at the location is so important that we give the location the name critical point .
  ::extrema和衍生物的位置在位置上的这种关系非常重要,以至于我们给出了地点的名称关键点。

  播放段落

  We will call $\begin{align*}x=c\end{align*}$  a critical point in the closed interval $\begin{align*}[a, b]\end{align*}$ if $\begin{align*}f(c)\end{align*}$ exists, and either  $\begin{align*}f^\prime(c)=0\end{align*}$ or  $\begin{align*}f^\prime(c)\end{align*}$ does not exist.
  ::如果f(c)存在,而且f*(c)=0或f*(c)不存在,我们将在封闭间隔[a,b]中将x=c称为临界点。

  播放段落

  Summary so far: If a function is continuous in a closed interval, it has both a minimum and a maximum at some location(s), and the derivative at these locations is either 0 or does not exist. The locations are called critical points.
  ::至今为止的摘要:如果一项函数在封闭的间隔内连续进行,则在某些地点有最低和最高值,而这些地点的衍生物要么0,要么不存在。这些地点被称为临界点。

  播放段落

  The  diagram below explicitly identifies  how to identify critical points. The end points of the closed interval are included as critical points if we consider the function only defined on the closed interval and not outside the interval. In this case, the derivative at each end point would not be defined.
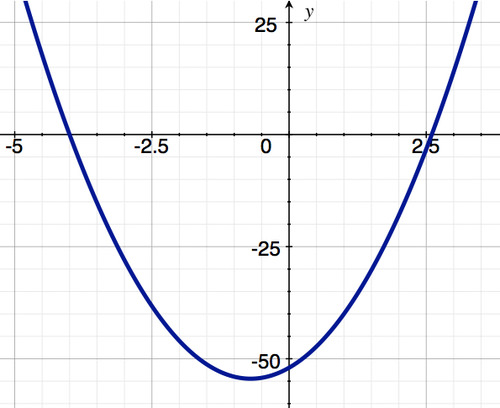
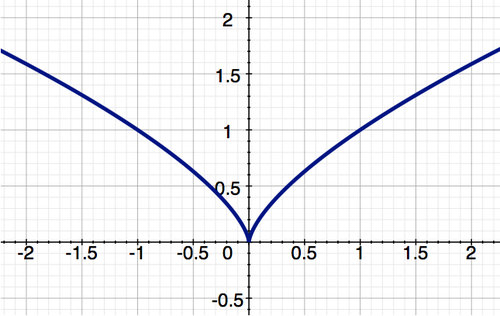
  ::下图明确指出了如何识别关键点。 如果我们考虑到该函数仅在封闭间隔而不是间隔之外所定义的功能, 封闭间隔的终点就被列为关键点。 在这种情况下, 将不会定义每个终点的衍生物 。

  

  播放段落

  Let’s consider the two functions shown below and say something about them in the closed interval [-2, 2]. Notice that  $\begin{align*}g(x)\end{align*}$  (the second function) has a cusp at $\begin{align*}x=0\end{align*}$ .
  ::让我们来考虑下面显示的两个函数,然后在封闭的间隔[-2, 2] 中对它们发表一些看法。请注意 g(x) (第二个函数) 在 x=0 时有一个角值 。

  

  

  播放段落

  Two functions
  ::两项职能

  播放段落

  Both functions are continuous in [-2, 2]. By the Extreme Value Theorem  they both have a minimum and maximum. As the table shows,  $\begin{align*}f(x)\end{align*}$ has a an extreme value where $\begin{align*}f^\prime(x)=0\end{align*}$ , and  $\begin{align*}g(x)\end{align*}$ has an extreme value where  $\begin{align*}g^\prime(x)\end{align*}$ is not defined. These are critical points.
  ::两种函数在 [-2, 2] 中都是连续的。根据极端值定理,它们都有最小值和最大值。如表所示,f(x) 具有极端值,而f(x) =0 和 g(x) 具有极值,而g(x) 则没有定义。这些是关键点。

  Function Property	$\begin{align*}f(x)=5x^2+7x-52\end{align*}$	$\begin{align*}g(x)=x^{\frac{2}{3}}\end{align*}$
  Value at endpoint $\begin{align*}x=-2\end{align*}$	-46	1.59
  Value at endpoint $\begin{align*}x=2\end{align*}$	-18	1.59
  Location and value where $\begin{align*}f^\prime(x)=0\end{align*}$	(-0.7, -54.45)	---
  Location where  $\begin{align*}f^\prime(x)\end{align*}$ Does Not Exist	End points	Endpoints, $\begin{align*}x=0\end{align*}$
  Critical point(s)	$\begin{align*}x=-0.7\end{align*}$ End points	$\begin{align*}x=0\end{align*}$ , End points
  Minimum value and location(s)	(-0.7, -54.45)	(0, 0)
  Location(s) of Maximum value	(2, -18)	(-2, 1.59) (2, 1.59)

  播放段落

  It should be noted that the converse of the Extreme Value Theorem is not necessarily true, i.e., just because $\begin{align*}f^{\prime}(x)=0\end{align*}$  at some location $\begin{align*}x=a\end{align*}$ , the function value $\begin{align*}f(a)\end{align*}$  does not have to be a local minimum or maximum.
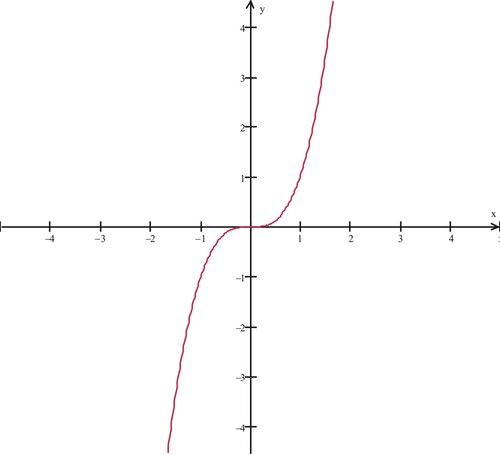
  ::应当指出,极端价值理论的反义不一定是真实的,即仅仅因为在某个地点x=a的f`(x)=0,函数值f(a)不一定必须是当地最低值或最高值。

  播放段落

  Consider $\begin{align*}f(x)=x^3\end{align*}$  and its graph. We see that while $\begin{align*}f^{\prime}(0)=0\end{align*}$  at  $\begin{align*}x=0\end{align*}$ ,  $\begin{align*}x=0\end{align*}$ is not an extreme point of the function.
  ::考虑 f( x) =x3 及其图形。 我们可以看到, f}( 0) =0 at x=0, x=0 不是函数的极端点 。

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to  determine how the derivative of the quadratic function  $\begin{align*}(y=ax^2+bx+c)\end{align*}$ and the vertex formula   $\begin{align*}x=-\frac{b}{2a}\end{align*}$  are related.
  ::早些时候, 您被要求确定二次函数( y=ax2+bx+c) 和顶点公式 xb2a 的衍生物是如何关联的 。

  播放段落

  If you realized that the vertex of the quadratic function is also the location where the slope of the tangent line, and therefore the derivative, equals 0 you made a great observation. $\begin{align*}\frac{dy}{dx}=2ax+b=0\end{align*}$  means that $\begin{align*}x=-\frac{b}{2a}\end{align*}$ . This is the $\begin{align*}x\end{align*}$ -value of the vertex, and a critical value or point of the function.
  ::如果您意识到二次函数的顶点也是正切线的斜度, 也就是衍生物的斜度, 等于 0, 您做了一个伟大的观察。 dydx=2ax+b=0 表示 xb2a。 这是顶点的 x 值, 以及函数的临界值或点 。

  播放段落

  Example 2
  ::例2

  播放段落

  The function $\begin{align*}f(x)=\sqrt{25-x^2}\end{align*}$  is the upper portion of a circle centered at (0, 0) with radius 5. Find the critical points of the function, and the maxima and minima.
  ::函数 f( x) = 25 - x2 是圆的上半径为 0, 0 的圆的上半部, 半径为 5 。 查找函数的临界点, 以及最大值和最小值 。

  播放段落

  Compute the derivative: $\begin{align*}f^{\prime}(x)=\frac{1}{2 \sqrt{25-x^2}}(-2x)=-\frac{x}{\sqrt{25-x^2}}\end{align*}$
  ::计算衍生物: f( x) = 1225- x2( - 2x) x25- x2

  播放段落

  $\begin{align*}f^{\prime}(x)=0\end{align*}$  means $\begin{align*}x=0\end{align*}$  is a critical point, and $\begin{align*}f(0)=5\end{align*}$ .
  ::f_(x)=0 表示x=0是一个临界点, f_(0)=5 表示x=0是一个临界点。

  播放段落

  Notice that  $\begin{align*}f^{\prime}(x)\end{align*}$ is undefined at the two locations $\begin{align*}x=\pm 5\end{align*}$ , which means these are criticial points. Both of the values are associated with function values $\begin{align*}f(\pm 5)=0\end{align*}$ .
  ::注意 f} (x) 在两个位置 x} 5 尚未定义, 这意味着这些是批评点。 这两个值都与函数值 f 5 = 0 有关 。

  播放段落

  The function minima are at (-5, 0) and (5, 0); the function maximum is at (0, 5).
  ::功能微型在(5,0)和(5,0);功能最大在(0,5);功能最大在(0,5)。

  播放段落

  Review
  ::回顾

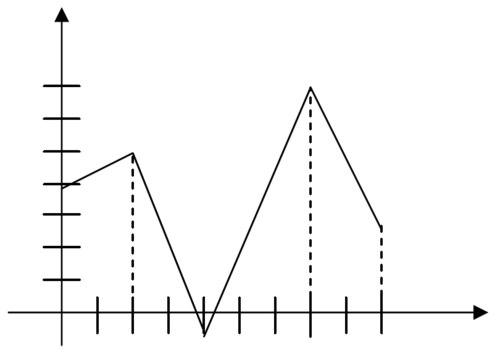
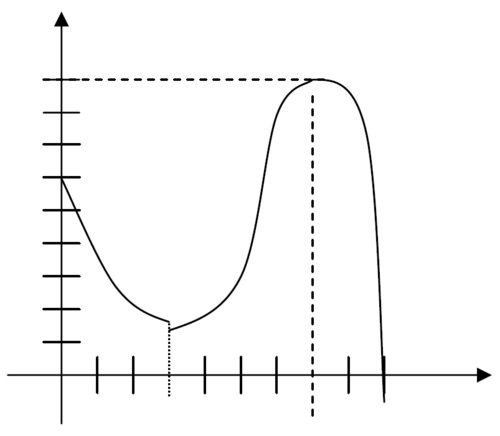
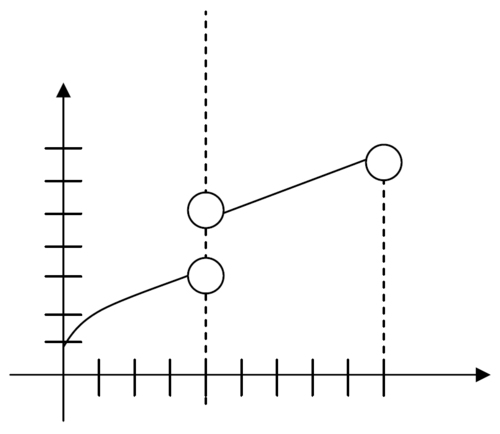
  播放段落

  For  #1-3, identify the absolute and local minimum and maximum values of the function (if they exist); find the extrema. (Units on the axes indicate1 unit).
  ::# 1-3, 标明函数的绝对值和本地最小值和最大值(如果存在的话); 找到 extrema 。 (轴上的单位表示 1 个单位)。

  播放段落
  1. Continuous on [0, 9]
     ::[0, 9]时连续

  

  播放段落
  2. Continuous on [0, 9]
     ::[0, 9]时连续

  

  播放段落
  3. Continuous on $\begin{align*}[0, 4] \cup [4, 9]\end{align*}$
     ::[0,4][4,9]

  

  播放段落

  For  #4–6, find the extrema and sketch the graph.
  ::4-6, 找到外形并绘制图表。

  播放段落
  4. $\begin{align*}f(x)=-x^2-6x+4 \end{align*}$ , [-4, 1]
     ::f(x) x2 - 6x+4, [4, 1]
  播放段落
  5. $\begin{align*}f(x)=x^3-x^4\end{align*}$ , [0, 2]
     :xx)=x3-x4, [0, 2]
  播放段落
  6. $\begin{align*}f(x)=-x^2+\frac{4}{x^2} \end{align*}$ , [-2, 0]
     ::f(xx) x2+4x2, [-2, 0]
  播放段落
  7. What is the absolute maximum of the sine function over the interval $\begin{align*}[0, \pi]\end{align*}$ ?
     ::间隔[0]内正弦函数的绝对最大值是多少?
  播放段落
  8. What are the local minimums of the cosine function over the interval $\begin{align*}[0, 2 \pi]\end{align*}$ ?
     ::间隔 [0,2] 的余弦函数的本地最小值是多少 ?
  播放段落
  9. What is the absolute maximum and absolute minimum of the function  $\begin{align*}x^2 \end{align*}$ over the interval [6, 7]?
     ::间隔内函数 x2 的绝对最大和绝对最小值是多少[6、7]?
  播放段落
  10. At what point does the function $\begin{align*}f(x)=(x^2-7x-8)^4\end{align*}$  attain its absolute minimum over the interval [5, 10]?
      ::F(x) =(x2- 7x-8) 4 的函数在间隔[5, 10] 达到其绝对最小值的什么时候?
  播放段落
  11. Let  $\begin{align*}[a, b]\end{align*}$ be a closed, finite interval, and let  $\begin{align*}f(x)\end{align*}$ be a straight line. If  $\begin{align*}f(x)\end{align*}$ achieves its maximum value over  $\begin{align*}[a, b]\end{align*}$ at points other than  $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ , what must be true about $\begin{align*}f(x)\end{align*}$ ?
      ::让[a,b]成为封闭的、有限的间隔,让f(x)成为一条直线。如果f(x)在除a和b以外的点上达到[a,b]的最大值,f(x)必须什么是真实的?
  播放段落
  12. Find all the critical numbers of $\begin{align*}f(x)=3x^4-\frac{8}{3}x^3-6x^2+8x+1\end{align*}$ .
      ::查找 f( x) = 3x4 - 83x3 - 6x2+8x+1 的所有关键数字。
  播放段落
  13. Find all the critical numbers of $\begin{align*}f(x)=\frac{1}{2x^2-5x-3}\end{align*}$ .
      ::查找 f( x) = 12x2 - 5x-3 的所有关键数字 。
  播放段落
  14. Find all the critical numbers of $\begin{align*}f(x)=\ln(x-4)\end{align*}$ .
      ::查找 f( x) =ln ( x- 4) 的所有关键数字 。
  播放段落
  15. Find all the critical numbers of $\begin{align*}f(x)=\sqrt{x} \times(1-x)\end{align*}$ .
      ::查找 f( x) =xx( 1- x) 的所有关键数字 。
  播放段落
  16. Find all the critical numbers of $\begin{align*}f(x)=\frac{x^2+x+1}{x-2}\end{align*}$ .
      ::查找 f( x) =x2+x+1x-2 的所有关键数字。
  播放段落
  17. Does the polynomial  $\begin{align*}f(x)=x^6+x^4+x^2+1\end{align*}$ attain a minimum value over the interval $\begin{align*}[-\pi, \pi]\end{align*}$ ?
      ::多角 f( x) =x6+x4+x2+1 是否在间隔内达到最小值 [, ] ?
  播放段落
  18. Does the function  $\begin{align*}f(x)=7^{\sin (x)}\end{align*}$ attain a maximum value over the interval $\begin{align*}(0, \pi)\end{align*}$ ?
      ::函数 f( x) = 7sin {( x) 是否在间隔( 0 ) 内达到最大值 ?
  播放段落
  19. Does the function  $\begin{align*}f(x)=\frac{10}{x}\end{align*}$ attain a maximum value over the interval [-1, 1]?
      ::函数 f( x) =10x 是否在间隔[ 1 - 1] 内达到最大值 ?
  播放段落
  20. Does the function  $\begin{align*}f(x)=\sin \left(\frac{x}{2} \right)\end{align*}$ attain a minimum value over the interval $\begin{align*}(0, \pi)\end{align*}$ ?
      ::函数 f( x) =sin ( x2) 是否在间隔( 0 ) 内达到最小值 ?
  播放段落
  21. Let  $\begin{align*}a\end{align*}$ and  $\begin{align*}b\end{align*}$ be two positive number such that $\begin{align*}a < b\end{align*}$ . Does the function  $\begin{align*}f(x)=\ln(x)\end{align*}$ attain a maximum value over the interval $\begin{align*}[a, b]\end{align*}$ ?
      ::让 a 和 b 成为两个正数, 即 a<b。 函数 f( x) =ln ( x) 是否在间隔[ a, b] 内达到最大值 ?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。