4.3 中值理论

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 中值定理

  Collapse Expand

  中值定理

  播放段落

  Jim was telling his math major friend about a speeding ticket he had received recently for going over 80 mph one weekend morning when there was little traffic on the highway. Apparently two police officers at different locations along the highway had recorded him going 60 and 65 mph respectively as he went by each of their speed trap positions. Jim said he knew where the speed traps were located and always made sure he was within the speed limit going by, so he could not understand how they could say he was speeding. Jim’s math major friend asked whether the officer who issued the ticket had said anything. Jim recalled that the officer had mentioned that the speed traps were exactly 3 miles apart, and that they knew Jim’s car had covered the distance in 2 minutes. Jim’s math major friend smiled and said, “Oh, that’s how they did it: The Mean Value Theorem”. Jim looked very perplexed.
  ::吉姆告诉他的数学主要朋友,他最近收到一张超速罚单,他最近收到一张超速罚单,因为一个周末早上,高速公路上交通很少。 显然,高速公路上不同地点的两名警官记录他经过每个速度陷阱位置时,分别走60和65英里。 吉姆说他知道速度陷阱的位置,并且总是确保他处于速度限制之内,所以他不明白他们怎么能说他超速。 吉姆的数学主要朋友问开罚单的军官是否说了什么。 吉姆回忆说,快速陷阱完全相距3英里,他们知道吉姆的车在2分钟内就到达了距离。 吉姆的数学主要朋友笑着说 , “ 哦,他们就是这样做的 : 中值理论 ” 。 吉姆看起来很困惑。

  播放段落

  Can you figure out how the police officer could have issued a ticket without actually witnessing Jim’s car going over 80 mph?
  ::警方若不亲眼目睹Jim的车驶过80英里, 怎会发票?

  播放段落

  The Mean Value Theorem
  ::中值定理

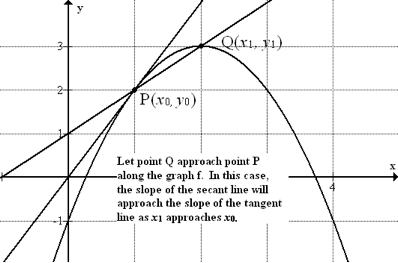
  播放段落

  In an earlier concept, the derivative of a function was introduced as the slope of the tangent line at a point. We looked at how the slope of a secant line changed as one of the two points approached the other. The secant line became the tangent line in the limit as illustrated below.
  ::在早先的一个概念中,函数的衍生物被作为正切线的斜坡引入到一个点上。我们查看了偏差线的斜坡是如何随着两点之一接近另一点而变化的。伸线成为下限的正切线,如下文所示。

  

  播放段落

  Now we look at the slope values of tangent lines in an interval defined by the secant line between two points. The following theorem gives an important relationship.
  ::现在我们在两个点之间的分离线界定的间隔内查看正切线的斜度值。下面的定理提供了一个重要的关系。

  播放段落

  Rolle’s Theorem:   If  $\begin{align*}f\end{align*}$ is continuous on a closed interval $\begin{align*}[a,b]\end{align*}$  and differentiable on the open interval $\begin{align*}(a, b)\end{align*}$ , and if  $\begin{align*}f(a)=f(b)\end{align*}$ then  $\begin{align*}f\end{align*}$ has at least one value  $\begin{align*}c\end{align*}$ in the open interval  $\begin{align*}(a,b)\end{align*}$ such that $\begin{align*}f^\prime(c)=0\end{align*}$ .
  ::Rolle的定理:如果 f 在一个封闭的间隔[a,b]上是连续的,在开放间隔(a,b)上是可区分的,如果 f(a)=f(b),那么f 在开放间隔(a,b)中至少有一个值c,例如 f`(c)=0。

  播放段落

  Let’s see if you can make use of Rolle’sTheorem
  ::让我们看看能否利用罗乐的理论

  播放段落

  For the function $\begin{align*}f(x)=x^2-3x-10\end{align*}$ , show that it satisfies the conditions of Rolle’s theorem on the interval [-2, 5] and find all numbers  $\begin{align*}c\end{align*}$ in (-2, 5) that satisfy $\begin{align*}f^\prime(c)=0\end{align*}$
  ::函数 f( x) =x2- 3x- 10, 显示它满足了 [-2, 5] 间隔期间 Rolle 的定理条件, 并查找满足 f_ (c) =0 的 f( 2) = 5 中的所有 c 数字。

  

  播放段落

  Evaluating  $\begin{align*}f(x)\end{align*}$ at  $\begin{align*}x=-2\end{align*}$ and  $\begin{align*}x=5\end{align*}$ yields :
  ::在 x2 和 x= 5 产量处评估 f(x) :

  播放段落

  $$\begin{align*}f(-2) &=(-2)^2-3(-2)-10\\ &=0\\ f(5) &=(5)^2-3(5)-10\\ &=0\end{align*}$$
  ::f(-2) = (-2) = (-2) 2-3(-2) - 10= 0f(5) = (5) = (5) = 3(5) - 10= 0

  播放段落

  Therefore $\begin{align*}f(-2)=f(5)\end{align*}$ , which satisfies the conditions for Rolle’s theorem to hold.
  ::因此,f(-2)=f(5),满足了罗尔尔理论维持的条件。

  播放段落

  Now to find values of  $\begin{align*}c\end{align*}$ that satisfy $\begin{align*}f^\prime(c)=0\end{align*}$ .
  ::现在可以找到满足 f_(c) =0 的 c 值。

  播放段落

  $$\begin{align*}\frac{dy}{dx} &=2x-3\\ f^\prime(c)&=0\\ &=2(c)-3\\ \therefore c&=\frac{3}{2}\end{align*}$$
  :c)=0=2(c) -3c=32

  播放段落

  So $\begin{align*}f^\prime \left(\frac{3}{2}\right)=0\end{align*}$  satisfies Rolle’sTheorem.
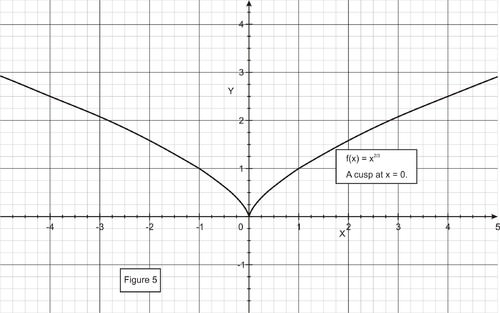
  ::所以F_(32)=0满足罗尔的理论。

  播放段落

  Consider the function $\begin{align*}f(x)=x^{\frac{2}{3}}\end{align*}$ . On the interval [-4, 4], $\begin{align*}f(-4)=f(4)\end{align*}$ . However, is there any point at which the derivative of $\begin{align*}f(x)=x^{\frac{2}{3}}\end{align*}$  is equal to zero? Is this a contradiction of Rolle's theorem ?
  ::考虑函数 f( x) =x23。 在间隔 [-4 , f(-4) = f(4) 。 但是, f( x) =x23 的衍生物是否等于零? 这是否与 Rolle 的定理相矛盾 ?

  播放段落

  The function curve for $\begin{align*}f(x)=x^{\frac{2}{3}}\end{align*}$  is shown below.
  ::F( x) =x23 的函数曲线如下所示。

  

  播放段落

  It’s derivative is $\begin{align*}f^\prime(x)=\frac{2}{3x^{\frac{1}{3}}}\end{align*}$ , which is undefined at $\begin{align*}x=0\end{align*}$ , and there is no point at which the derivative is 0. But, because the function is not differentiable over the interval, Rolle’sTheorem does not apply. There is no contradiction.
  ::它的衍生物是F`(x)=23x13,在 x=0 时未定义,也没有衍生物为 0 的点。 但是,由于该函数在间隔期间无法区分, Rolle 的理论不适用。 不存在矛盾。

  播放段落

  Rolle’s Theorem requires that $\begin{align*}f(a) = f(b)\end{align*}$ . But Rolle’s theorem is the basis for proving the important general theorem called the Mean Value Theorem which does not require $\begin{align*}f(a) = f(b)\end{align*}$ .
  ::Rolle的定理要求 f(a) = f(b) 。 但是, Rolle 的定理是证明所谓的 " 平均值理论 " 这一重要总定理的基础,它不需要 f(a) = f(b) 。

  播放段落

  Mean Value Theorem:  If  $\begin{align*}f\end{align*}$ is a continuous function on a closed interval  $\begin{align*}[a,b]\end{align*}$ and if  $\begin{align*}f^\prime\end{align*}$ contains the open interval  $\begin{align*}(a,b)\end{align*}$ in its domain, then there exists a number  $\begin{align*}c\end{align*}$ in the interval  $\begin{align*}(a,b)\end{align*}$ such that
  ::平均值值定理:如果 f 是封闭间隔[a,b] 的连续函数,如果 f 在其域内含有开放间隔(a,b),那么在间隔(a,b)中就存在一个数字 c,因此

  播放段落

  $$\begin{align*}f^\prime(c)=\frac{f(b)-f(a)}{b-a}\end{align*}$$
  ::f_(c)=f(b)-f(a)b-a

  播放段落

  An equivalent form is:  $\begin{align*}f(b)-f(a)=(b-a)f^\prime(c)\end{align*}$ .
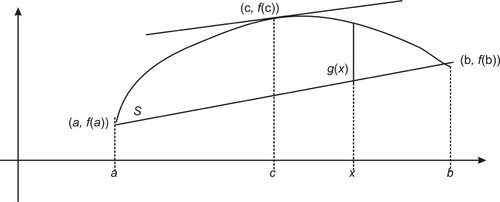
  ::等效形式是:f(b)-f(a)=(b)-a)f_(c)。

  播放段落

  An illustration of the meaning of the Mean Value Theorem is shown in the figure below, where the slope of the secant line connecting  $\begin{align*}f(a)\end{align*}$ and  $\begin{align*}f(b)\end{align*}$ can be found to be the same as the slope of the tangent line at $\begin{align*}f(c)\end{align*}$ .
  ::下图显示了平均值理论的含义,其中可发现连接f(a)和f(b)的分离线的斜坡与f(c)的正切线的斜坡相同。

  

  播放段落

  Verify that the Mean Value Theorem applies for the function  $\begin{align*}f(x)=x^3+3x^2-24x\end{align*}$ on the interval [1, 4].
  ::校验平均值定理是否适用于间隔[1, 4] 中的函数 f(x)=x3+3x2-24x。

  播放段落

  We need to find  $\begin{align*}c\end{align*}$ in the interval (1, 4) such that $\begin{align*}f^\prime(c) =\frac{f(4)-f(1)}{(4-1)}\end{align*}$
  ::我们需要在间隔(1,4)中找到c,这样f*(c)=f(4)-f(1)(4-1)

  播放段落

  $$\begin{align*}f^\prime(c) &=\frac{f(4)-f(1)}{(4-1)}\\ &=\frac{16+20}{3}\\ &=12\end{align*}$$
  ::f_(c)=f(4)-f(1)(4-1)=16+203=12

  播放段落

  Note that
  ::请注意

  播放段落

  $\begin{align*}f^\prime (x)=3x^2+6x-24,\end{align*}$
  ::f_(x)=3x2+6x-24,

  播放段落

  Hence, we must solve the following equation:
  ::因此,我们必须解决以下等式:

  播放段落

  $$\begin{align*}3c^2+6c-24&=12\\ 3c^2+6c-32 &=0\\ c^2+2c-12 &=0\\ c &=-1\pm\sqrt{13}\end{align*}$$
  ::3c2+6c-24=123c2+6c-32=0c2+2c-12=0c113

  播放段落

  Since we need to have  $\begin{align*}c\end{align*}$ in the interval (1, 4), the positive root is the solution:
  ::由于我们需要在间隔(1,4)内有c,积极的根源是解决办法:

  播放段落

  $\begin{align*}c\approx2.61.\end{align*}$
  ::c2.61。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked about how Jim could get a speeding ticket for going at least 80 mph when his car’s speed was recorded at 60 mph and 65 mph.
  ::先前有人问及Jim在车速为60米和65米时, 如何获得超速罚单,

  播放段落

  The key information was that the police officer determined that Jim had traveled 3 miles in 2 minutes, so that Jim’s average speed was 90 mph. Jim’s math major friend knew that by the Mean Value Theorem there had to have been at least one time when Jim’s actual speed was 90 mph, definitely exceeding 80 mph.
  ::关键信息是该警官确定吉姆在2分钟内行驶了3英里,因此吉姆的平均速度是90英里。 吉姆的数学主要朋友知道,根据中值理论,至少有一次吉姆的实际速度是90英里,绝对超过80英里。

  播放段落

  Example 2
  ::例2

  播放段落

  Verify that the Mean Value Theorem applies for the function  $\begin{align*}f(x)=2\sin x+3\cos x\end{align*}$ on the interval $\begin{align*}(0, 2\pi )\end{align*}$ .
  ::校验平均值定理是否适用于间隔( 0,2) f(x) = 2sinx+3cosx) 函数 。

  播放段落

  We need to find  $\begin{align*}c\end{align*}$ in the interval $\begin{align*}(0, 2\pi )\end{align*}$ such that $\begin{align*}f^\prime(c)=\frac{f(2\pi)-f(0)}{(2\pi-0)}\end{align*}$ :
  ::我们需要在间隔(0,2)内找到c, 以便 f'(c) = f(2) - f(0) (20) :

  播放段落

  $$\begin{align*}f^\prime(c)&=\frac{f(2\pi)-f(0)}{(2\pi-0)}\\ &=\frac{2-2}{2\pi}\\ &=0\end{align*}$$
  ::f_(c) = f(2__) - f(0)(2__0) = 2-22-22_0

  播放段落

  Note that
  ::请注意

  播放段落

  $\begin{align*}f^\prime(x)=2\cos x-3\sin x\end{align*}$
  ::f_(x) = 2cosx- 3sinx

  播放段落

  Hence, we must solve the following equation:
  ::因此,我们必须解决以下等式:

  播放段落

  $$\begin{align*}2\cos c-3\sin c &=0\\ \tan c &=\frac{2}{3}\\ c &=\tan^{-1}\left(\frac{2}{3}\right)\\ c &=0.588 \ \text{radians} \ \ldots \ \text{and also} \ (0.588+\pi) \ \text{radians in the interval} \ (0,2\pi).\end{align*}$$
  ::2c-3sinc=0tanc=23c=tan-1(23)c=0.588弧度.以及(0.588)间隔内(0,2)弧度。

  播放段落

  The Mean Value Theorem applies in two places in the interval $\begin{align*}(0,2\pi)\end{align*}$ .
  ::中值定理在间隔( 0,2) 的两个地方适用( 0,2)。

  播放段落

  Review
  ::回顾

  播放段落

  For #1-5, if possible, verify Rolle’s Theorem for the following functions by finding values of $\begin{align*}x\end{align*}$  for which $\begin{align*}f(x)=0\end{align*}$  and $\begin{align*}f^\prime(x)=0\end{align*}$ . If it is not possible, state why.
  ::对于 # 1 5, 如果可能的话, 校验 Rolle 的理论, 通过查找 f( x) = 0 和 f* ( x) = 0 的 x 值, 来校验以下函数的理论。 如果不可能的话, 请说明原因 。

  播放段落
  1. $\begin{align*}f(x)=3x^3-12x\end{align*}$
     :xx) = 3x3 - 12x
  播放段落
  2. $\begin{align*}f(x)=x^2-\frac{2}{x-1}\end{align*}$
     :xx) =x2-2x-1
  播放段落
  3. $\begin{align*}f(x)=-2x^2-12x+5\end{align*}$
     :xx)%% 2x2 - 12x+5
  播放段落
  4. $\begin{align*}f(x)=|2x-3|\end{align*}$
     :xx)%%2x-3________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
  播放段落
  5. $\begin{align*}f(x)=2\sin x+3\cos x\end{align*}$
     ::f(x) = 2辛x+3cosx
  播放段落
  6. $\begin{align*}f(x)=x^4-2x^2\end{align*}$
     :xx) =x4-2x2
  播放段落
  7. Prove that if the equation $\begin{align*}x^3+a_1x^2+a_2x=0\end{align*}$  has a positive root at $\begin{align*}x=r\end{align*}$  and that the equation $\begin{align*}3x^2+2a_1x+a_2=0\end{align*}$ has a positive root less than $\begin{align*}r\end{align*}$ .
     ::证明如果方程式 x3+a1x2+a2x=0 在 x=r 有正根,而方程式 3x2+2a1x+a2=0 的正根小于 r。

  播放段落

  For #8-15, verify that the Mean Value Theorem works for each function in the specified interval, or state why it does not.
  ::对于 # 8-15 , 校验平均值定理是否在指定间隔内为每个函数工作, 或者说明为何没有工作 。

  播放段落
  8. $\begin{align*}f(x)=\frac{(x+2)}{x}\end{align*}$ , [1, 2]
     :xx)=(x+2)x,[1,2]
  播放段落
  9. $\begin{align*}f(x)=\frac{2}{x}\end{align*}$ , [-1,1]
     ::f(x)=2x, [-1, 1]
  播放段落
  10. $\begin{align*}f(x)=x^2-5x+1\end{align*}$ , [0, 3]
      ::f(x) =x2-5x+1, [0, 3]
  播放段落
  11. $\begin{align*}f(x)=5-\frac{4}{x}\end{align*}$ , [1, 4]
      :xx)=5-4x, [1, 4]
  播放段落
  12. $\begin{align*}f(x)=x^3-8x-5\end{align*}$ , [1, 4]
      :xx)=x3-8x-5,[1,4]
  播放段落
  13. $\begin{align*}f(x)=\sin x\end{align*}$ , $\begin{align*}\left[0,\frac{\pi}{2} \right]\end{align*}$
      ::f(x) =sinx, [0]2]
  播放段落
  14. $\begin{align*}f(x)=\cos x\end{align*}$ , $\begin{align*}\left[0,\frac{\pi}{2} \right]\end{align*}$
      ::f(x) =cosx, [0]2]
  播放段落
  15. $\begin{align*}f(x)=2^x\end{align*}$ , [0, 3]
      ::f(x)=2x, [0, 3]

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。