4.8 分析函数图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 分析函数图

  Collapse Expand

  分析函数图

  播放段落

  Given a set of information on the key properties of a function, you can sketch the graph. Before we proceed, make an attempt to summarize for what you think are key properties. Often, the key properties of a function are not all presented to you directly, but must be determined from the information at hand.
  ::根据函数关键属性的一组信息,您可以绘制图表。在我们继续之前,尝试对您认为的关键属性进行总结。通常,函数的关键属性并非全部直接呈现给您,而必须从手头的信息中确定。

  播放段落

  Analyzing Graphs of Functions
  ::函数分析图

  播放段落

  We will first summarize the kind of information about functions we now can generate based on our previous concepts . Then we will use this information to analyze examples of representative rational, polynomial, radical, and trigonometric functions.
  ::我们首先总结一下我们现在能够根据我们以前的概念产生的关于功能的信息类型。 然后我们将利用这些信息分析具有代表性的合理、多元、激进和三角功能的例子。

  播放段落

  Let's use a table like the one shown as a template to organize our findings.
  ::让我们用一张像显示为模板的表格 来组织我们的调查结果。

  Table Summary

  $\begin{align*}f(x)=\end{align*}$	Analysis
  Domain and Range
  Intercepts and Zeros
  Asymptotes and limits at infinity
  Differentiability
  Intervals where   $\begin{align*}f\end{align*}$ is increasing
  Intervals where   $\begin{align*}f\end{align*}$ is decreasing
  Relative extrema
  Concavity
  Inflection points

  播放段落

  Analyzing Rational Functions
  ::分析逻辑函数

  播放段落

  Consider the rational function $\begin{align*}f(x)=\frac{x^2-4}{x^2-2x-8}\end{align*}$ .
  ::考虑合理的函数 f( x) =x2 - 4x2 - 2x-8 。

  播放段落

  Zeroes, Domain, and Range
  ::零度、域域和范围

  播放段落

  The function appears to have zeros at $\begin{align*}x=\pm 2\end{align*}$ . However, once we factor the expression we see
  ::此函数似乎在 x @ @ @ {% 2 时为零 。 但是, 一旦我们将表达式乘以, 我们可以看到

  播放段落

  $\begin{align*}\frac{x^2-4}{x^2-2x-8}=\frac{(x+2)(x-2)}{(x-4)(x+2)}=\frac{x-2}{x-4}\end{align*}$ .
  ::x2-4x2-2x-8=(x+2)(x-2)(x-4)(x+2)=x-2x-4。

  播放段落

  Hence, the function has a zero at $\begin{align*}x=2\end{align*}$ , there is a hole in the graph at $\begin{align*}x=-2\end{align*}$ , the domain is $\begin{align*}(-\infty, -2) \cup (-2,4) \cup (4, + \infty)\end{align*}$ , and the $\begin{align*}y\end{align*}$ -intercept is at $\begin{align*}\left(0, \frac{1}{2}\right)\end{align*}$ .
  ::因此,函数在x=2时为零,在x=2时为零,图中在x=2时为空洞,域为(,-2)(-2)(-2,4)(4, )(4, ),y-interview在(0, 12)时为空洞。

  播放段落

  Asymptotes and Limits at Infinity
  ::无限的零年和限制

  播放段落

  Given the domain, we note that there is a vertical asymptote at $\begin{align*}x=4\end{align*}$ . To determine other asymptotes, we examine the limit of  $\begin{align*}f\end{align*}$ as  $\begin{align*}x \rightarrow \infty\end{align*}$ and $\begin{align*}x \rightarrow -\infty\end{align*}$ . We have
  ::鉴于域,我们注意到在 x=4 上有一个垂直的静态。为了确定其他的静态,我们检查 f 作为 x 和 x 的极限。 我们检查了 f 作为 x 和 x 的极限 。

  播放段落

  $\begin{align*}\lim_{x \rightarrow \infty} \frac{x^2-4}{x^2-2x-8}=\lim_{x \rightarrow \infty} \frac{\frac{x^2}{x^2}-\frac{4}{x^2}}{\frac{x^2}{x^2}-\frac{2x}{x^2}-\frac{8}{x^2}}=\lim_{x \rightarrow \infty} \frac{1-\frac{4}{x^2}}{1-\frac{2}{x}-\frac{8}{x^2}}=1\end{align*}$ .
  ::立方公尺x2 - 4x2 - 2x8=limxx*x2 - 4x2 - 4x2x2 - 4x2x2 - 2x2 - 8x2=limx*1 - 4x2 - 2x8x2=1

  播放段落

  Similarly, we see that $\begin{align*}\lim_{x \rightarrow -\infty} \frac{x^2-4}{x^2-2x-8}=1\end{align*}$ . We also note that  $\begin{align*}y \neq \frac{2}{3}\end{align*}$ since $\begin{align*}x \neq -2\end{align*}$ .
  ::类似地,我们也看到 limxx2 -4x2 -2x-8=1. 我们还注意到,自xxx2以来,y23。

  播放段落

  Hence we have a horizontal asymptote at $\begin{align*}y=1\end{align*}$ .
  ::因此,我们有一个在y=1的横向空位。

  播放段落

  Differentiability
  ::可区别性

  播放段落

  $\begin{align*}f^\prime (x)=\frac{-2x^2-8x-8}{(x^2-2x-8)}=\frac{-2}{(x-4)^2} < 0\end{align*}$ . Hence the function is differentiable at every point of its domain, and since $\begin{align*}f^\prime (x)<0\end{align*}$  on its domain, then $\begin{align*}f\end{align*}$  is decreasing on its domain, $\begin{align*}(-\infty, -2) \cup (-2, 4) \cup (4, + \infty)\end{align*}$ .
  ::f2x2-8x-8(x2-2x-8) 2(x-4)2 < 0。 因此,函数在其域的每个点上都是可区别的,并且自其域上F(x) <0)以来,F在其域上正在下降,(,-2) (-2) (4) (4) 。

  播放段落

  $\begin{align*}f^{\prime\prime} (x)=\frac{4}{(x-4)^3}\end{align*}$ .
  ::f*(x)=4(x-4)3。

  播放段落

  $\begin{align*}f^{\prime\prime} (x) \neq 0\end{align*}$  in the domain of $\begin{align*}f\end{align*}$ . Hence there are no relative extrema and no inflection points.
  ::ff. f. f. (x)%% 0 在 f. 领域。 因此,没有相对的extrema 和 没有反射点 。

  播放段落

  So  $\begin{align*}f^{\prime\prime} (x)>0\end{align*}$ when $\begin{align*}x>4\end{align*}$ . Hence, the graph is concave up for  $\begin{align*}x>4\end{align*}$ .
  ::f( xx) > 0 时为 x> 4。 因此, 图形为 x> 4 调整 。

  播放段落

  Similarly, $\begin{align*}f^{\prime\prime}(x)<0\end{align*}$  when $\begin{align*}x<4\end{align*}$ . Hence, the graph is concave down for $\begin{align*}x<4, x \neq -2\end{align*}$ .
  ::同样, f( xx) < 0 时为 x < 4 。 因此, 图表以 x< 4, x% 2 向下粘结 。

  播放段落

  Let’s summarize our results in the table before we sketch the graph.
  ::让我们在绘制图表之前先在表格中总结一下我们的结果。

  Table Summary

  $\begin{align*}f(x)=\frac{x^2-4}{x^2-2x-8}\end{align*}$	Analysis
  Domain and Range	播放段落 $\begin{align*}D=(-\infty, -2) \cup (-2,4) \cup (4, + \infty)\end{align*}$ ::D=(,-2) (-2,4) (4, ) 播放段落 $\begin{align*}R=\{ \text{all reals} \neq 1 \text{or} \ \frac{2}{3}\}\end{align*}$ ::Rall reals *1or 23} 所有的房地产*1或23}
  Intercepts and Zeros	播放段落 Zero at $\begin{align*}x=2\end{align*}$ , ::x=2时为零,x=2时为零; 播放段落 $\begin{align*}y-\end{align*}$ intercept at $\begin{align*}\left(0, \frac{1}{2}\right)\end{align*}$ ::- 在(0,12)拦截y-拦截(0,12)
  Asymptotes and limits at infinity	播放段落 VA at $\begin{align*}x=4\end{align*}$ , ::x=4, VA 值为 x=4, 播放段落 HA at $\begin{align*}y=1\end{align*}$ , ::HA y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y y, y= 1, y= 1, y y, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, y= 1, 1, y= 1, y= 1, 1, y= 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 播放段落 Hole in the graph at $\begin{align*}x=-2\end{align*}$ ::x% 2 的图形洞洞
  Differentiability	Differentiable at every point of its domain
  Intervals where   $\begin{align*}f\end{align*}$ is increasing	Nowhere
  Intervals where   $\begin{align*}f\end{align*}$ is decreasing	$\begin{align*}(-\infty, -2) \cup (-2,4) \cup (4, + \infty)\end{align*}$
  Relative extrema	None
  Concavity	播放段落 Concave up in $\begin{align*}(4, + \infty)\end{align*}$ , ::集中起来( 4, , , , , , , , , , , , , ) 播放段落 Concave down in $\begin{align*}(-\infty, -2) \cup (-2,4)\end{align*}$ ::隐藏在 (,-2) \\\\\\\\\\ - 2,4)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
  Inflection points	播放段落 None ::无无无无无无无

  Finally, we sketch the graph as follows:

  播放段落

  Analyzing Radical Functions
  ::分析激进函数

  播放段落

  Now, Consider the function $\begin{align*}f(x)=\sqrt{2x-1}\end{align*}$ .
  ::现在, 考虑函数 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\ f f( x)\\\\\\\\ 1 。

  播放段落

  Zeroes, Domain, and Range
  ::零度、域域和范围

  播放段落

  The domain of $\begin{align*}f\end{align*}$  is $\begin{align*}\left(\frac{1}{2}, + \infty \right)\end{align*}$ , and it has a zero at $\begin{align*}x=\frac{1}{2}\end{align*}$ .
  ::f 的域为 (12, ) , 在 x= 12 时为零 。

  播放段落

  Asymptotes and Limits at Infinity
  ::无限的零年和限制

  播放段落

  Given the domain, we note that there are no vertical asymptotes. We note that $\begin{align*}\lim_{x \rightarrow \infty} f(x)=+\infty\end{align*}$ .
  ::鉴于这个域,我们注意到没有垂直的微粒。我们注意到, limxf(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Differentiability
  ::可区别性

  播放段落

  $\begin{align*}f^\prime (x)=\frac{1}{\sqrt{2x-1}}>0\end{align*}$  for the entire domain of $\begin{align*}f\end{align*}$ . Hence  $\begin{align*}f\end{align*}$ is increasing everywhere in its domain. $\begin{align*}f^\prime (x)\end{align*}$  is not defined at $\begin{align*}x=\frac{1}{2}\end{align*}$ , so $\begin{align*}x=\frac{1}{2}\end{align*}$  is a critical value.
  ::f* (x) = 12x- 1>0 整个 f 域。 因此, f 在其域内无处不在增加 。 f* (x) 在 x= 12 时没有定义, 所以 x= 12 是一个关键值 。

  播放段落

  $\begin{align*}f^{\prime\prime}(x)=\frac{-1}{\sqrt{(2x-1)^3}}<0\end{align*}$  everywhere in $\begin{align*}\left(\frac{1}{2}, +\infty\right)\end{align*}$ . Hence $\begin{align*}f\end{align*}$  is concave down in $\begin{align*}\left(\frac{1}{2}, +\infty\right)\end{align*}$ .
  ::f(x)11(2x-1)3<0无处不在 (12,)。 f因此在(12,)。

  播放段落

  $\begin{align*}f^\prime (x)\end{align*}$  is not defined at $\begin{align*}x=\frac{1}{2}\end{align*}$ , so $\begin{align*}x=\frac{1}{2}\end{align*}$  is an absolute minimum.
  ::f_(x) 在 x=12 时没有定义, 所以 x=12 是绝对最低值 。

  Table Summary

  $\begin{align*}f(x)=\sqrt{2x}-1\end{align*}$	Analysis
  Domain and Range	播放段落 $\begin{align*}D=\left(\frac{1}{2}, +\infty \right), R=\{y \ge 0 \}\end{align*}$ ::D=( 12, , ,
  Intercepts and Zeros	播放段落 Zero at $\begin{align*}x=\frac{1}{2}\end{align*}$ , ::x=12时为零, 播放段落 No $\begin{align*}y-\end{align*}$ intercept ::无法 y- 拦截
  Asymptotes and limits at infinity	播放段落 No asymptotes ::无小星点图条
  Differentiability	Differentiable in $\begin{align*}\left(\frac{1}{2}, +\infty \right)\end{align*}$
  Intervals where   $\begin{align*}f\end{align*}$ is increasing	Everywhere in $\begin{align*}D=\left(\frac{1}{2}, + \infty \right)\end{align*}$
  Intervals where   $\begin{align*}f\end{align*}$ is decreasing	Nowhere
  Relative extrema	None
  Concavity	播放段落 Absolute minimum at $\begin{align*}x=\frac{1}{2}\end{align*}$ , located at $\begin{align*}\left(\frac{1}{2}, 0 \right)\end{align*}$ ::x=12时的绝对值最低值(12,0) 播放段落 Concave down in $\begin{align*}\left(\frac{1}{2}, + \infty \right)\end{align*}$ ::收缩在( 12, @ @ @ @ @ @ )
  Inflection points	播放段落 None ::无无无无无无无

  播放段落

  Here is a sketch of the graph:
  ::以下是图表的草图:

  

  播放段落

  Analyzing Trigonometric Functions
  ::分析三角函数

  播放段落

  We will see that while trigonometric functions can be analyzed using what we know about , they will provide some interesting challenges that we will need to address.
  ::我们将看到,虽然可以利用我们所了解的情况来分析三角函数,但它们将提供一些我们需要应对的有趣挑战。

  播放段落

  Consider the function $\begin{align*}f(x)=x-2 \sin x\end{align*}$  on the interval $\begin{align*}[-\pi, \pi]\end{align*}$ .
  ::考虑间隔的函数 f( x) =x- 2sinx [, ] 。

  播放段落

  Zeroes, Domain, and Range
  ::零度、域域和范围

  播放段落

  We note that $\begin{align*}f\end{align*}$  is a continuous function and attains an absolute maximum and minimum in $\begin{align*}[-\pi, \pi]\end{align*}$ . Its domain is $\begin{align*}[-\pi, \pi]\end{align*}$ , and its range is $\begin{align*}R=\{ -\pi \le y \le \pi \}\end{align*}$ .
  ::我们注意到,f是一个连续的功能,在[,]达到绝对的上限和最低限值,其范围是[,],其范围是R。

  播放段落

  Differentiability
  ::可区别性

  播放段落

  $\begin{align*}f^\prime (x)=1-2 \cos x=0\end{align*}$  at $\begin{align*}x=-\frac{\pi}{3}, \frac{\pi}{3}\end{align*}$ .
  ::f_(x) = 1 - 2cosx= 0 at x% 3,%3 。

  播放段落

  Note that  $\begin{align*}f^\prime (x) > 0\end{align*}$ on $\begin{align*}\left(-\pi, -\frac{\pi}{3}\right)\end{align*}$  and $\begin{align*}\left(\frac{\pi}{3}, \pi \right)\end{align*}$ ; therefore the function is increasing in $\begin{align*}\left(-\pi, - \frac{\pi}{3}\right)\end{align*}$  and $\begin{align*}\left(\frac{\pi}{3}, \pi\right)\end{align*}$ .
  ::请注意 f(x)>0 和 (,3) ; 因此,该函数在(,3) 和 (3) 中正在增加 。

  播放段落

  Note that $\begin{align*}f^\prime (x) < 0\end{align*}$  on $\begin{align*}\left(-\frac{\pi}{3}, \frac{\pi}{3}\right)\end{align*}$ ; therefore the function is decreasing in $\begin{align*}\left(-\frac{\pi}{3}, \frac{\pi}{3}\right)\end{align*}$ .
  ::注意 f_(x) <0 on (3,_3) ; 因此,该功能在(3,_3) 中正在下降 。

  播放段落

  $\begin{align*}f^{\prime\prime} (x)=2 \sin x=0\end{align*}$  if $\begin{align*}x=0, \pi, -\pi\end{align*}$ . Hence the critical values are at $\begin{align*}x=-\pi, -\frac{\pi}{3}, \frac{\pi}{3}\end{align*}$ , and $\begin{align*}\pi\end{align*}$ .
  ::f*(x) = 2sinx=0 如果 x=0, 则x=0, {}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\3,\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  $\begin{align*}f^{\prime\prime} \left(\frac{\pi}{3}\right)>0\end{align*}$ ; hence there is a relative minimum at $\begin{align*}x=\frac{\pi}{3}\end{align*}$ .
  ::f*( 3) > 0; 因此在 x% 3 有相对最小值 。

  播放段落

  $\begin{align*}f^{\prime\prime} \left(-\frac{\pi}{3}\right)<0\end{align*}$ ; hence there is a relative maximum at $\begin{align*}x=-\frac{\pi}{3}\end{align*}$ .
  ::f(3) <0; 因此在 x3 有相对的上限 。

  播放段落

  $\begin{align*}f^{\prime\prime} (x) <0\end{align*}$  on  $\begin{align*}(-\pi, 0)\end{align*}$ and  $\begin{align*}f^{\prime\prime} (x) > 0\end{align*}$ on $\begin{align*}(0, \pi)\end{align*}$ . Hence the graph is concave down on $\begin{align*}(-\pi, 0)\end{align*}$ and concave up and decreasing on $\begin{align*}(0, \pi)\end{align*}$ . There is an inflection point at  $\begin{align*}x=0\end{align*}$ , located at the point (0, 0).
  ::f(x) <0 on (,0) 和 f(x)>0 on (0,0) 。 因此, 图形在( ,0) 上沉, 在( 0,0) 上沉, 在( 0,0) 上沉, 在( 0) 上沉, 在( 0,0) 上沉。 x=0 上有一个反射点 。

  播放段落

  Finally, there is absolute minimum at $\begin{align*}x=-\pi\end{align*}$ , located at  $\begin{align*}(-\pi, -\pi)\end{align*}$ , and an absolute maximum at  $\begin{align*}x=\pi\end{align*}$ , located at $\begin{align*}(\pi, \pi)\end{align*}$ .
  ::最后,位于(,)的x绝对最低值和位于(,)的x绝对最高值。

  Table Summary

  $\begin{align*}f(x)=x-2 \sin x\end{align*}$	Analysis
  Domain and Range	播放段落 $\begin{align*}D=[-\pi, \pi], R=\{-\pi \le y \le \pi\}\end{align*}$ ::D=[,],Ry
  Intercepts and Zeros	播放段落 $\begin{align*}x=-\frac{\pi}{3}, \frac{\pi}{3}\end{align*}$ ::x3,%3
  Asymptotes and limits at infinity	播放段落 No asymptotes ::无小星点图条
  Differentiability	Differentiable in $\begin{align*}D=[-\pi, \pi]\end{align*}$
  Intervals where   $\begin{align*}f\end{align*}$ is increasing	$\begin{align*}\left(\frac{\pi}{3}, \pi \right)\end{align*}$ and $\begin{align*}\left(-\pi, -\frac{\pi}{3}\right)\end{align*}$
  Intervals where   $\begin{align*}f\end{align*}$ is decreasing	$\begin{align*}\left(-\frac{\pi}{3}, \frac{\pi}{3}\right)\end{align*}$
  Relative extrema	播放段落 Relative maximum at $\begin{align*}x=-\frac{\pi}{3}\end{align*}$ ::在 x% 3 时的相对最大值 播放段落 Relative minimum at $\begin{align*}x=\frac{\pi}{3}\end{align*}$ ::相对最小值 x% 3
  Concavity	播放段落 Absolute maximum at $\begin{align*}x=\pi\end{align*}$ , located at $\begin{align*}(\pi, \pi)\end{align*}$ ::位于 (______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 播放段落 Absolute minimum at $\begin{align*}x=-\pi\end{align*}$ , located at $\begin{align*}(-\pi, -\pi)\end{align*}$ Concave up in $\begin{align*}(0, \pi)\end{align*}$ ::位于 (, ) 封存于 (0, ) 的 x 的绝对值最小值 。
  Inflection points	播放段落 $\begin{align*}x=0\end{align*}$ , located at the point (0, 0) ::x=0,位于点(0,0)

  播放段落

  Here is a sketch of the graph:
  ::以下是图表的草图:

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to summarize the key properties of functions. As you have seen in this concept, key properties of functions include: domain, range, intercepts, asymptotes (including limits at infinity), , increasing and decreasing intervals, extrema, concavity, and points of inflection.
  ::早些时候, 您被要求总结函数的关键属性 。 正如您在此概念中看到的那样, 函数的关键属性包括: 域、 范围、 拦截、 微粒( 包括无限限制 ) 、 增加和减少间隔、 extrema、 concavity 和 切换点 。

  播放段落

  Example 2
  ::例2

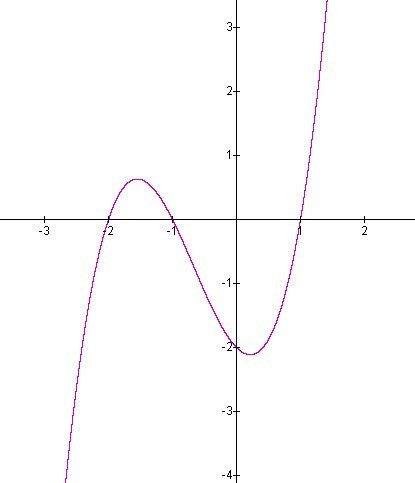
  播放段落

  Consider the polynomial function $\begin{align*}f(x)=x^3+2x^2-x-2\end{align*}$ .
  ::考虑多边函数 f( x) =x3+2x2- x-2 。

  播放段落

  Zeroes, Domain, and Range
  ::零度、域域和范围

  播放段落

  The domain of  $\begin{align*}f\end{align*}$ is  $\begin{align*}(-\infty, +\infty)\end{align*}$ and the $\begin{align*}y\end{align*}$ -intercept at (0, -2).
  ::f 的域是 (, ) 和 y interview at (0, 2) 。

  播放段落

  The function can be factored  $\begin{align*}f(x)=x^3+2x^2-x-2=x^2 (x+2)-1(x+2)=(x^2-1)(x+2)=(x-1)(x+1)(x+2)\end{align*}$
  ::函数可以乘以 f(x) =x3+2x2x2- x2=x2(x+2)- 1(x+2)=(x2- 1)(x+2)=(x- 1)(x+2)=(x- 1)(x+1)(x+1)(x+2) =(x- 1)(x+1)(x+2)

  播放段落

  and thus has zeros at $\begin{align*}x=\pm 1, -2\end{align*}$ .
  ::因此在 x1, - 2 时为零。

  

  播放段落

  
  Asymptotes and Limits at infinity
  ::无限的微量和限制

  播放段落

  Given the domain, we note that there are no vertical asymptotes. We note that and $\begin{align*}\lim_{x \to \infty} f(x)=+ \infty\end{align*}$ and $\begin{align*}\lim_{x \to -\infty} f(x)=-\infty\end{align*}$ .
  ::鉴于这个域,我们注意到没有垂直的静态。我们注意到了这一点,以及limxf(x)和limxf(x)。

  播放段落

  Differentiability
  ::可区别性

  播放段落

  $\begin{align*}f^\prime (x)=3x^2+4x-1=0\end{align*}$  if $\begin{align*}x=\frac{-4 \pm \sqrt{28}}{6}=\frac{-2 \pm \sqrt{7}}{3}\end{align*}$ . These are the critical values. We note that the function is differentiable at every point of its domain.
  ::f*( x) = 3x2+4x- 1=0 如果 x @ @ @ @ @ @ @ @ @ @ @ @ @ 286 @ @ @ @ @ @ 73) 。 这些是关键值。 我们注意到, 函数在其域的每个点都是不同的 。

  播放段落

  $\begin{align*}f^\prime (x) >0\end{align*}$  on  $\begin{align*}\left(-\infty, \frac{-2-\sqrt{7}}{3}\right)\end{align*}$ and $\begin{align*}\left(\frac{-2 + \sqrt{7}}{3}, + \infty\right)\end{align*}$ ; hence the function is increasing in these intervals.
  ::f(x)>0 on (,-273) 和 (-273,) ; 因此,这些间隔期间该函数正在增加 。

  播放段落

  Similarly,  $\begin{align*}f^\prime (x) <0\end{align*}$ on  $\begin{align*}\left(\frac{-2-\sqrt{7}}{3}, \frac{-2+\sqrt{7}}{3}\right)\end{align*}$ and thus is  $\begin{align*}f\end{align*}$ decreasing there.
  ::同样,在(-)273,-273)上,F`(x)<0,因此,在下降。

  播放段落

  $\begin{align*}f^{\prime\prime} (x)=6x+4=0\end{align*}$  if  $\begin{align*}x=-\frac{2}{3}\end{align*}$ where there is an inflection point.
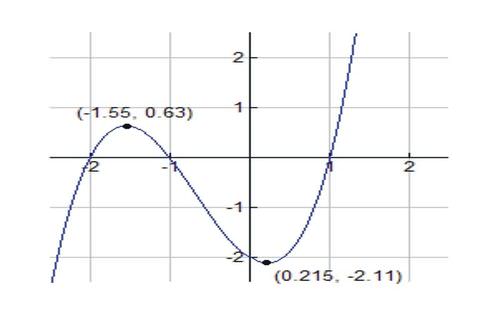
  ::f( x) = 6x+4=0 如果 x\\ 23 存在点, 则 f( x) = 6x+4=0 。

  播放段落

  In addition, $\begin{align*}f^{\prime\prime} \left(\frac{-2-\sqrt{7}}{3}\right)<0\end{align*}$ . Hence the graph has a relative maximum at  $\begin{align*}x=\frac{-2-\sqrt{7}}{3}\end{align*}$ and located at the point (-1.55, 0.63).
  ::此外,f(-273)<0.。因此,图表在x273处的相对最高值为x273,位于点(1.55,0.63)。

  播放段落

  We note that $\begin{align*}f^{\prime\prime} (x) <0\end{align*}$ for $\begin{align*}x<-\frac{2}{3}\end{align*}$ . The graph is concave down in $\begin{align*}\left(-\infty, -\frac{2}{3}\right)\end{align*}$ .
  ::我们注意到, f( x) < 0 表示 x23。 图表在( , − 23 ) 中进行粘结 。

  播放段落

  And we have $\begin{align*}f^{\prime\prime} \left(\frac{-2+\sqrt{7}}{3} \right)>0\end{align*}$ ; hence the graph has a relative minimum at  $\begin{align*}x=\frac{-2+\sqrt{7}}{3}\end{align*}$ and located at the point (0.22, -2.11).
  ::我们有 f(-273)>0; 因此, 图形在 x273 时的相对最小值是 x273, 位于点( 0. 22, - 2. 11) 。

  播放段落

  We note that  $\begin{align*}f^{\prime\prime} (x) >0\end{align*}$ for $\begin{align*}x>-\frac{2}{3}\end{align*}$ . The graph is concave up in $\begin{align*}\left(-\frac{2}{3}, + \infty \right)\end{align*}$ .
  ::我们注意到 f(x)>0 表示 x23 。 图表在( ~ 23) 中 。

  Table Summary

  $\begin{align*}f(x)=x^3+2x^2-x-2\end{align*}$	Analysis
  Domain and Range	播放段落 $\begin{align*}D=(-\infty, + \infty), R=\{\text{all reals} \}\end{align*}$ ::D=(,,,),Rall reals}
  Intercepts and Zeros	播放段落 Zeros at $\begin{align*}x=\pm 1, -2, y,\end{align*}$ intercepts at (0, -2) ::x% 1, -2, y, 拦截时间( 0, 2) 时为零
  Asymptotes and limits at infinity	播放段落 No asymptotes ::无小星点图条
  Differentiability	Differentiable at every point of it's domain
  Intervals where   $\begin{align*}f\end{align*}$ is increasing	$\begin{align*}\left(-\infty, \frac{-2-\sqrt{7}}{3}\right)\end{align*}$ and $\begin{align*}\left(\frac{-2+\sqrt{7}}{3}, + \infty \right)\end{align*}$
  Intervals where   $\begin{align*}f\end{align*}$ is decreasing	$\begin{align*}\left(\frac{-2-\sqrt{7}}{3}, \frac{-2+\sqrt{7}}{3}\right)\end{align*}$
  Relative extrema	播放段落 Relative maximum at $\begin{align*}x=\frac{-2-\sqrt{7}}{3}\end{align*}$ and located at the point (-1.55, 0.63); ::在x273处的相对最大值为x273,位于点(1.55,0.63); 播放段落 Relative minimum at $\begin{align*}x=\frac{-2+\sqrt{7}}{3}\end{align*}$ and located at the point (0.22, -2.11). ::相对最小值 x273,位于点(0.22,-2.11)。
  Concavity	播放段落 Concave up in $\begin{align*}\left(-\frac{2}{3}, +\infty \right)\end{align*}$ . ::聚集在(-23)中。 播放段落 Concave down in $\begin{align*}\left(-\infty, -\frac{2}{3}\right)\end{align*}$ . ::隐藏在(,23)中。
  Inflection points	播放段落 $\begin{align*}x=-\frac{2}{3}\end{align*}$ , located at the point $\begin{align*}\left(-\frac{2}{3}, -.74\right)\end{align*}$ ::x23,位于点(-23,-.74)

  播放段落

  Here is a sketch of the graph:
  ::以下是图表的草图:

  

  播放段落

  Review
  ::回顾

  播放段落

  For all of the following functions, summarize the functions by filling out the table below. Use the information to sketch a graph of the function.
  ::对于以下所有函数,请通过填写下表来概括函数。使用这些信息绘制函数的图表。

  Table Summary

  $\begin{align*}f(x)=\end{align*}$	Analysis
  Domain and Range
  Intercepts and Zeros
  Asymptotes and limits at infinity
  Differentiability
  Intervals where   $\begin{align*}f\end{align*}$ is increasing
  Intervals where   $\begin{align*}f\end{align*}$ is decreasing
  Relative extrema
  Concavity
  Inflection points

  播放段落
  1. $\begin{align*}f(x)=x^3+3x^2-x-3\end{align*}$
     :xx) =x3+3x2-x3)
  播放段落
  2. $\begin{align*}f(x)=-x^4+4x^3-4x^2\end{align*}$
     :xx) x4+4x3-4x2
  播放段落
  3. $\begin{align*}f(x)=\frac{2x-2}{x^2}\end{align*}$
     :xx)=2x-2x2
  播放段落
  4. $\begin{align*}f(x)=x-x^{\frac{1}{3}}\end{align*}$
     :xx) =x-x13
  播放段落
  5. $\begin{align*}f(x)=-\sqrt{2x-6}+3\end{align*}$
     :xx)%%2x-6+3
  播放段落
  6. $\begin{align*}f(x)=x^2-2\sqrt{x}\end{align*}$
     :xx) =x2--2x
  播放段落
  7. $\begin{align*}f(x)=1+\cos x\end{align*}$ on the interval $\begin{align*}[-\pi, \pi]\end{align*}$
     ::间隔的 f(x) = 1+cosx [, ]
  播放段落
  8. $\begin{align*}f(x)=x^2-x+1\end{align*}$
     :xx) =x2 - x+1
  播放段落
  9. $\begin{align*}f(x)=4x^3-6x^2-1\end{align*}$
     :xx) = 4x3 - 6x2 - 1
  播放段落
  10. $\begin{align*}f(x)=\frac{x^2}{x-1}\end{align*}$
      :xx) =x2x-1
  播放段落
  11. $\begin{align*}f(x)=x^2 e^{-x}\end{align*}$
      :xx)=x2e-x)
  播放段落
  12. $\begin{align*}f(x)=\cos x-x\end{align*}$
      :x) =cosx-x
  播放段落
  13. $\begin{align*}f(x)=e^{-2x}+e^x\end{align*}$
      :xx) =e-2x+ex
  播放段落
  14. $\begin{align*}f(x)=5e^{-x}+x^3\end{align*}$
      :xx)=5e-x+x3
  播放段落
  15. $\begin{align*}f(x)=x^5-7x^2+2\end{align*}$
      :x) =x5 - 7x2+2

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。