5.10 数字集成:轨迹方法

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节数字集成:轨迹方法

  折叠 展开

  数字集成:轨迹方法

  播放段落

  Recall that we have used different ways to approximate the value of integrals. These included Riemann Sums using left and right endpoints, as well as midpoints for finding the length of each rectangular tile. In this lesson the rectangular tiles are replace by trapezoidal tiles to approximate the integral. Do you think that the use of trapezoids would give a more accurate result than the use of rectangles? Why? Can you think of a reason why the concavity of the function curve would matter in the accuracy of the area estimation using trapezoids?
  ::回顾我们使用不同方法来估计整体体的值。 其中包括使用左端和右端点的里曼 Sums, 以及查找每个矩形瓷砖长度的中点。 在这个教训中, 矩形瓷砖被陷阱化的瓷砖取代, 以接近整体体。 您是否认为使用矩形比使用矩形更准确的结果? 为什么? 您能想到函数曲线的混凝土对于使用三角形来估计面积的准确性很重要吗 ?

  播放段落

  The Trapezoidal Rule
  ::治病规则

  播放段落

  Recall that we used different ways to approximate the value of integrals. These included Riemann Sums using left and right endpoints, as well as midpoints for finding the length of each rectangular tile. In this lesson we will learn two other methods for approximating integrals. The first of these, the Trapezoidal Rule , uses areas of trapezoidal tiles to approximate the integral. The second method, Simpson’s Rule, uses to make the approximation.
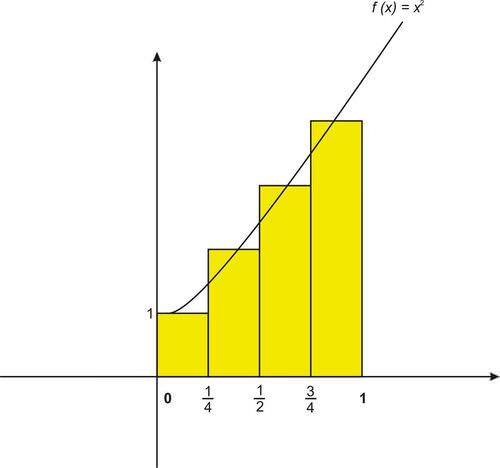
  ::回顾我们用不同方法来估计整体体的值。 其中包括使用左端和右端点的里曼点和中点来寻找每个矩形瓷砖的长度。 在这一教训中,我们将学习其他两种接近整体体的方法。 其中第一个方法,即“ 轨迹规则 ” , 使用区域捕捉式瓷砖来接近整体体。 第二个方法,辛普森规则,用近似法则。

  播放段落

  Let’s recall how we would use the midpoint rule with $\begin{align*}n=4\end{align*}$  rectangles to approximate the area under the graph of $\begin{align*}f(x)=x^2+1\end{align*}$  from $\begin{align*}x=0\end{align*}$  to $\begin{align*}x=1\end{align*}$ .
  ::让我们回顾一下我们如何使用带有 n=4 矩形的中点规则来接近 f( x) =x2+1 图下从 x=0 到 x=1 的面积。

  

  播放段落

  If instead of using the midpoint value within each sub-interval to find the length of the corresponding rectangle, we could have instead formed trapezoids by joining the maximum and minimum values of the function within each sub-interval:
  ::如果不是在每个次间隙内使用中点值来找到相应的矩形长度,我们本可以通过将每个次间隙内函数的最大值和最小值合并起来,从而形成围网类:

  

  播放段落

  The area of a trapezoid is $\begin{align*}A=\frac{h(b_1+b_2)}{2}\end{align*}$ , where $\begin{align*}b_1\end{align*}$  and $\begin{align*}b_2\end{align*}$  are the lengths of the parallel sides and $\begin{align*}h\end{align*}$  is the height. In our trapezoids the height is  $\begin{align*}\triangle x\end{align*}$ and $\begin{align*}b_1\end{align*}$  and $\begin{align*}b_2\end{align*}$ are the values of the function. Therefore in finding the areas of the trapezoids we actually average the left and right endpoints of each sub-interval.
  ::捕捉类动物的区域是 A =h (b1+b2 2 2), 其中 b1 和 b2 是平行边的长度, h 是高度。 在我们的捕捉类动物中, 高度是 x 和 b1 和 b2 是函数的值。 因此, 在找到捕捉类动物的区域时, 我们实际上平均了每个次interval 的左端和右端点 。

  播放段落

  Therefore a typical trapezoid would have the area
  ::因此,典型的类类动物将拥有这一区域。

  播放段落

  $$\begin{align*}A=\frac{\triangle x}{2}(f(x_{i-1})+f(x_i)).\end{align*}$$
  ::x2(f(xi-1)+f(xi))。

  播放段落

  To approximate $\begin{align*}\int\limits_{a}^{b}f(x)dx\end{align*}$  with $\begin{align*}n\end{align*}$  of these trapezoids, we have
  ::大约baf(x)dx与 n 这些捕捉类动物,我们有

  播放段落

  $$\begin{align*}\int\limits_{a}^{b}f(x)dx & \approx \frac{1}{2}\left[\sum_{i=1}^n f(x_i-1) \triangle x+\sum_{i=1}^n f(x_i)\triangle x\right] \\ &=\frac{\triangle x}{2}\left[f(x_0)+f(x_1)+f(x_1)+f(x_2)+f(x_2)+ \cdots+f(x_{n-1})+f(x_n)\right] \\ &=\frac{\triangle x}{2}\left[f(x_0)+2f(x_1)+2f(x_2)+ \cdots +2f(x_{n-1})+f(x_n)\right], \triangle x=\frac{b-a}{n}.\\\end{align*}$$
  :xxx)dx*% 12[ni=1f(xI- 1) x+ni=1f(xxx) x2[f(x0)+f(x1)+f(x1)+f(x2)+f(x2)+(x2)\f(x)+f(xn)]}x2[f(x0)+2f(x1)+2f(x1)+2f(x2)+2(x2)+(x1)+f(xn)],x=b-an。

  播放段落

  Apply the formula from above and use the Trapezoidal Rule to approximate $\begin{align*}\int\limits_{0}^{3}x^2 dx\end{align*}$  with $\begin{align*}n=6\end{align*}$ .
  ::从上面应用公式, 并使用“ 轨迹规则” 大约 30x2dx, 加上 n=6 。

  播放段落

  Each subinterval is $\begin{align*}\triangle x=\frac{b-a}{n}=\frac{3-0}{6}=\frac{1}{2}\end{align*}$ .
  ::每个次互动是 x=b -an=3-06=12。

  播放段落

  The integral approximation is:
  ::整体近似值是:

  播放段落

  $$\begin{align*}\int\limits_{0}^{3}x^2dx &\approx\frac{1}{4}\left[f(0)+2f\left(\frac{1}{2}\right)+2f(1)+2f\left(\frac{3}{2}\right)+2f(2)+2f\left(\frac{5}{2}\right)+f(3)\right]\\ &=\frac{1}{4}\left[0+\left(2\cdot\frac{1}{4}\right)+(2\cdot 1)+\left(2\cdot\frac{9}{4}\right)+(2\cdot4)+\left(2\cdot\frac{25}{4}\right)+9\right]\\ &=\frac{1}{4}\left[\frac{73}{2}\right]=\frac{73}{8}=9.125.\end{align*}$$
  ::0x2dx14[f(0)+2f(12)+2f(1)+2f(32)+2f(2)+2f(52)+f(3)]=14[0+2(2)14]+(2)1+(2)1)+(2(24)94+(2(24)4)+(2(24)2454+9]=14[732]=738=9.125。

  播放段落

  An exact solution can be determined by using the with the Fundamental Theorem. 
  ::确切的解决办法可以通过使用基本理论来确定。

  播放段落

  $\begin{align*}\int\limits_{0}^{3}x^2 dx=\frac{x^3}{3}\Big|_0^3=9\end{align*}$ .
  ::3 0x2dx=x33=30=9

  播放段落

  The error is about 1.4%.
  ::错误大约为1.4%。

  播放段落

  For some integrals it is impossible to find an antiderivative and a numerical method is the only option.
  ::对于某些整体体来说,不可能找到一种抗降解方法,而数字方法是唯一的选择。

  播放段落

  When this is the case, accuracy of the approximation is an issue. In particular, how large should  $\begin{align*}n\end{align*}$ be so that the trapezoidal estimate is accurate to within a given value, say 0.001?
  ::当情况如此时,近似值的准确性就是一个问题。 特别是,应该有多大的数值才能使诱杀性亚甲醚估计值准确到某一数值范围内,例如0.001?

  播放段落

  The magnitude of the error in using the trapezoidal technique for a given value of $\begin{align*}n\end{align*}$  can be shown to be:
  ::对于 n 的给定值, 使用捕捉杀虫技术时出错的大小可以显示为 :

  播放段落

  $\begin{align*}\left|Error _{Trapezoidal}\right| \le\frac{k(b-a)^3}{12 \ n^2}\end{align*}$ , where $\begin{align*}|f^{\prime \prime}(x)|\le k\end{align*}$  for $\begin{align*}a\le x\le b\end{align*}$ .
  :b-a)312 n2, f(x)k xb。

  播放段落

  This means that choosing $\begin{align*}n \ge \sqrt{\frac{k(b-a)^3}{12 \cdot |Error_{Trapezoidal}|}}\end{align*}$  will meet or exceed a specified error $\begin{align*}Error_{Trapezoidal}\end{align*}$ .
  ::这意味着选择 nk(b-a)312 Error Trapezoidal 将满足或超过指定错误 错误 错误

  播放段落

  Find  $\begin{align*}n\end{align*}$ so that the Trapezoidal Estimate for $\begin{align*}\int\limits_{0}^{3}x^2 dx\end{align*}$  is accurate to 0.001.
  ::查找 n 以便 3 0x2dx 的轨迹估计值准确到 0.001 。

  播放段落

  We need to find $\begin{align*}n\end{align*}$  such that $\begin{align*}|Error_{Trapezoidal}|\le 0.001 .\end{align*}$
  ::我们需要找到 最差的抗逆转录病毒药物 0.001

  播放段落

  First note that $\begin{align*}|f^{\prime \prime}(x)|=2\end{align*}$  for $\begin{align*}0\le x\le 3\end{align*}$ . Hence we can take $\begin{align*}k=2\end{align*}$  to find our error bound.
  ::第一个注意是 0x3 的 f(x)2 。 因此我们可以使用 k=2 来找到我们的错误 。

  播放段落

  $$\begin{align*}|Error_{Trapezoidal}|\le \frac{2(3-0)^3}{12 \ n^2}=\frac{54}{12 \ n^2}.\end{align*}$$
  :3-0)312 n2=5412 n2。

  播放段落

  We need to solve the following inequality for $\begin{align*}n\end{align*}$ :
  ::我们需要解决n的以下不平等问题:

  播放段落

  $$\begin{align*}\frac{54}{12\ n^2} &<0.001,\\ n^2 &>\frac{54}{12(0.001)},\\ n &>\sqrt{\frac{54}{12(0.001)}}\approx 67.08.\end{align*}$$
  ::5412 n2<0.001,n2>5412(0.001),n5412(0.0001)\\67.08。

  播放段落

  Hence we must take  $\begin{align*}n=68\end{align*}$ to achieve the desired accuracy.
  ::因此,我们必须使用n=68,才能达到预期的准确度。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if  you think that using trapezoids to approximate the area under a curve would give a more accurate result than using rectangles. Can you think of a reason why the concavity of the function curve would matter in the accuracy of the area estimation using trapezoids?
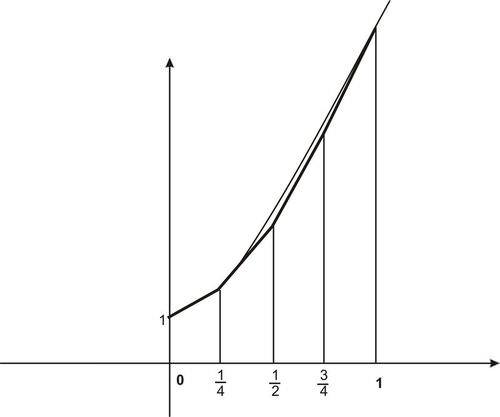
  ::早些时候, 有人问您是否认为使用 cugezoids 来接近曲线下的区域比使用矩形得出更准确的结果。 您能想到为什么函数曲线的精度会在使用 capezoids 进行区域估计的精度方面很重要吗 ?

  播放段落

  If you think that the use of trapezoids would give a more accurate result (with number of subintervals the same) you are correct. With some examples, you can see visually that the trapezoids cover the better. Notice, though, that if the function curve is concave up, the trapezoids will overestimate the area; if the concavity is down, the trapezoids will underestimate the area.
  ::如果您认为使用 cugaezoids 会给出一个更准确的结果( 与次对数相同 ) , 您是正确的 。 举例来说, 您可以看到, cugaezoids 覆盖得更好 。 但是, 请注意, 如果函数曲线在叠叠, 捕捉ezoids 将会高估区域; 如果混凝土在下降, cugaezoids 将会低估区域 。

  播放段落

  Example 2
  ::例2

  播放段落

  Use the Trapezoidal Rule to approximate $\begin{align*}\int\limits_{0}^{2}x^3 dx\end{align*}$  for $\begin{align*}n=4\end{align*}$ . Round the answer to four decimal places and compare this value to the exact value of the integral. What is the expected error for $\begin{align*}n=4\end{align*}$ ?
  ::N=4 使用“轨迹规则”大约为 20x3dx 。将答案四舍五入到小数点后四位位,然后将该值与积分的准确值进行比较。 n=4 的预期错误是什么?

  播放段落

  We find each subinterval as $\begin{align*}\triangle x=\frac{b-a}{n}=\frac{2-0}{4}=\frac{1}{2}\end{align*}$ .
  ::我们发现每个次interval 以 x=b -an=2 -04=12 表示 。

  播放段落

  The integral approximation is evaluated as follows:
  ::对整体近似值的评估如下:

  播放段落

  $$\begin{align*}\int\limits_{0}^{2}x^3 dx &\approx \frac{1}{4} \left[f(0)+2f(0.5)+2f(1)+2f(1.5)+f(2)\right] \\ &\approx\frac{1}{4} \left[0+2\cdot 0.125+2\cdot 1+2\cdot 3.375+8\right] \\ \int\limits_{0}^{2}x^3 dx &\approx 4.25 \end{align*}$$
  ::=========================================================================================================================================2.======================2.============================================================================================================================================================================================================================================================================================================================================================

  播放段落

  The estimate of the integral is 4.25.
  ::综合体估计数为4.25。

  播放段落

  The exact value of the integral: $\begin{align*}\int\limits_{0}^{2}x^3dx=\frac{x^4}{4}\Big|_0^2=4\end{align*}$ .
  ::积分的准确值: 20x3dx=x44=20=4。

  播放段落

  The error between these is 0.25.
  ::这两者之间的误差是0.25。

  播放段落

  The expected error using $\begin{align*}n=4\end{align*}$ :
  ::使用 n=4 的预期错误 :

  播放段落

  For $\begin{align*}f^{\prime \prime}(x)=6x,\ f^{\prime \prime}(x)\le 6 \cdot 2=12\end{align*}$ in the interval $\begin{align*}[0,2]\end{align*}$ .
  ::f(x) = 6x, f(x) 62= 12 间隔 [0. 2] 。

  播放段落

  Therefore, $\begin{align*}\left|Error_{Trapezoidal}\right| \le \frac{k(b-a)^3}{12 \ n^2}=\frac{12(2)^3}{12\cdot 4^2}=0.5\end{align*}$ .
  ::因此,“误杀”k(b-a)312n2=12(2)31242=0.5。

  播放段落

  The actual error is less than $\begin{align*}|Error_{Trapezoidal}|\end{align*}$ .
  ::实际误差小于 'Error Trapezodal' 。

  播放段落

  Example 3
  ::例3

  播放段落

  Use the Trapezoidal Rule to approximate $\begin{align*}\int\limits_{1}^{2}\frac{1}{(x+1)^2}dx\end{align*}$  for $\begin{align*}n=4\end{align*}$ . Round the answer to four decimal places and compare this value to the exact value of the integral. What is the expected error for $\begin{align*}n=4\end{align*}$ ?
  ::N=4 使用“轨迹规则”大约为 211( x+1)2dx 。 答案四舍五入到小数点后四位位数, 并比较此值与积分的准确值。 n=4 的预期错误是什么 ?

  播放段落

  We find each subinterval as $\begin{align*}\triangle x=\frac{b-a}{n}=\frac{2-1}{4}=\frac{1}{4}\end{align*}$ .
  ::我们发现每个次interval 都为 x=b -an=2 -14=14。

  播放段落

  The integral approximation is evaluated as follows:
  ::对整体近似值的评估如下:

  播放段落

  $$\begin{align*}\int\limits_{1}^{2}\frac{1}{(x+1)^2}dx & \approx\frac{1}{8} \left[f(2)+2f(2.25)+2f(2.5)+2f(2.75)+f(3)\right] \\ &\approx \frac{1}{8}\left[\frac{1}{4}+2\frac{1}{2.25^2}+2\frac{1}{2.5^2}+2\frac{1}{2.75^2}+\frac{1}{3^2}\right]\\ &\approx\frac{1}{8} \left[0.25+0.39506+0.32+0.26446+0.11111\right] \\ \int\limits_{1}^{2}\frac{1}{(x+1)^2}dx &\approx0.16758\approx 0.1676\end{align*}$$
  ::========================================================================================================================================================================+====================================================================================================================================================================================================================================================================================================================================================

  播放段落

  The estimate of the integral is 0.1676.
  ::积分估计数为0.1676。

  播放段落

  The exact value of the integral: $\begin{align*}\int\limits_{1}^{2}\frac{1}{(x+1)^2}dx=\frac{-1}{x+1}\Big|_1^2=\frac{1}{6}=0.1\overline{6}\end{align*}$ .
  ::积分的准确值 : 211( x+1) 2dx% 1x+1 @ 21=16=0. 1 =6 。

  播放段落

  The error between these is 0.0009.
  ::这两者之间的错误是 0.0009 。

  播放段落

  The expected error using $\begin{align*}n=4\end{align*}$ :
  ::使用 n=4 的预期错误 :

  播放段落

  For $\begin{align*}f^{\prime \prime}(x)=\frac{6}{(x+1)^4},\ f^{\prime \prime}(x)\le\frac{6}{(1+1)^4}=\frac{3}{8}=0.375\end{align*}$ in the interval [1, 2].
  ::f(x)=6(x+1)4, f(x)6(1+1)4=38=0.375 间隔[1、2]。

  播放段落

  Therefore, $\begin{align*}|Error_{Tropezoidal}|\le\frac{k(b-a)^3}{12n^2}=\frac{0.375(1)^3}{12\cdot 4^2}=0.001953\end{align*}$ .
  ::因此,“误杀”k(b-a)312n2=0.375(1)31242=0.001953。

  播放段落

  The actual error is less than $\begin{align*}|Error_{Trapeziodal}|\end{align*}$ .
  ::实际错误小于“Eror Trapeziodal ” 。

  播放段落

  Review
  ::回顾

  播放段落

  Use the Trapezoidal Rule to approximate the definite integrals using the given number of subintervals $\begin{align*}n\end{align*}$ .
  ::使用 " 轨迹规则 " ,使用给定的次隔热数 n 来接近确定的内分质。

  播放段落
  1. $\begin{align*}\int\limits_{1}^{7}(x+7)dx\end{align*}$  with $\begin{align*}n=6\end{align*}$ .
     ::71(x+7)dx, n=6。
  播放段落
  2. $\begin{align*}\int\limits_{-2}^{2}(x+4)dx\end{align*}$  with $\begin{align*}n=4\end{align*}$ .
     ::2(x+4)dx 带有 n=4 。
  播放段落
  3. $\begin{align*}\int\limits_{-4}^{1}(-x^2-2x+8)dx\end{align*}$  with $\begin{align*}n=5\end{align*}$ .
     ::4 (- x2 - 2x+8) dx, n= 5 。
  播放段落
  4. $\begin{align*}\int\limits_{2}^{7}\frac{2}{x}dx\end{align*}$  with  $\begin{align*}n=5\end{align*}$ .
     ::722xxxx加上 n=5
  播放段落
  5. $\begin{align*}\int\limits_{0}^{2}x^4dx\end{align*}$  with  $\begin{align*}n=4\end{align*}$ .
     ::2 0x4dx 带有 n=4 。
  播放段落
  6. $\begin{align*}\int\limits_{0}^{1}\sin x^2 dx\end{align*}$  with  $\begin{align*}n=4\end{align*}$ .
     ::1xx2dx和 n=4。
  播放段落
  7. $\begin{align*}\int\limits_{2}^{4}\sqrt{x}dx\end{align*}$  with  $\begin{align*}n=5\end{align*}$ .
     ::42xxxx和n=5
  播放段落
  8. $\begin{align*}\int\limits_{0}^{1}x^2e^{-x}dx\end{align*}$  with $\begin{align*}n=8\end{align*}$ .
     ::0x2e-xdx, n=8 。
  播放段落
  9. $\begin{align*}\int\limits_{1}^{4}\ln\sqrt{x}dx\end{align*}$  with  $\begin{align*}n=6\end{align*}$ .
     ::41lnxdx与 n=6 。
  播放段落
  10. $\begin{align*}\int\limits_{0}^{1}\sqrt{1+x^4}dx\end{align*}$  with  $\begin{align*}n=4\end{align*}$ .
      ::1 01+x4dx和n=4。
  播放段落
  11. $\begin{align*}\int\limits_{1}^{3}\frac{1}{x}dx\end{align*}$  with  $\begin{align*}n=8\end{align*}$ .
      ::311xdx与 n=8。
  播放段落
  12. $\begin{align*}\int\limits_{0}^{2}x^3dx\end{align*}$ for  $\begin{align*}n=8\end{align*}$ .
      ::n=8 的 0. 0x3dx
  播放段落
  13. Find a value of $\begin{align*}n\end{align*}$  that guarantees an error of no more than $\begin{align*}10^{-5}\end{align*}$  in the Trapezoidal approximation of $\begin{align*}\int\limits_{2}^{4}\sqrt{x}dx\end{align*}$ .
      ::查找 n 的值,保证在 42xdx 的 Trapioidal 近似值中发生不超过 10- 5 的错误。
  播放段落
  14. How large should $\begin{align*}n\end{align*}$ be so that the Trapezoidal Estimate for $\begin{align*}\int\limits_{1}^{3}\frac{1}{x}dx\end{align*}$  is accurate to within:
      1. 0.001?
      2. 0.00001?
      
      ::311xdx 的轨迹估计值准确到 0.001? 00001?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。