5.11 数字一体化:辛普森规则

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 数字整合:辛普森规则

  Collapse Expand

  数字整合:辛普森规则

  播放段落

  Recall that we have used different numerical methods to approximate the value of definite integrals. The methods we have looked at so far use rectangular or trapezoidal segmentation of the area under the function curve and might not be as accurate for functions where straight line segments are not the best approximation to the function curve. It is reasonable to think that other methods of approximating curves might be more applicable for some functions. Simpson’s Rule is a method that uses to approximate the curve instead of line segments. Do you think that the use of parabolas would give a more accurate result than the use of rectangles? Why? Can you think of any reason why the concavity of the function curve would matter in the accuracy of the area estimation using parabolas?
  ::回顾我们曾使用不同的数字方法来估计确定整体体的值。 我们迄今所研究的方法使用函数曲线下区域的矩形或角化分离法,对于直线部分不是函数曲线的最佳近似值的函数来说可能不准确。 有理由认为,其他近似曲线的方法可能更适用于某些函数。 辛普森的规则是用来接近曲线而不是线段的方法。 你认为使用parabolas会比使用矩形产生比使用矩形更准确的结果吗? 为什么? 你能想到为什么使用parapolas的函数曲线的共性会在区域估算的准确性中起到作用吗?

  播放段落

  Simpson's Rule
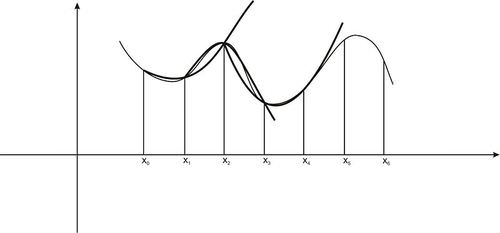
  ::辛普森规则

  播放段落

  As was true with the Trapezoidal Rule , for Simpson’s Rule the interval  $\begin{align*}[a, b]\end{align*}$ is divided into $\begin{align*}n\end{align*}$ sub-intervals of length $\begin{align*}\triangle x=\frac{b-a}{n} \end{align*}$ .
  ::辛普森规则的间隔[a,b] 被分为长度为 x=b-an的 n次间隔。

  播放段落

  Parabolas are then constructed through each group of three consecutive points on the graph. The graph below shows this process for the first three such parabolas for the case of  $\begin{align*}n=6\end{align*}$ sub-intervals. You can see that every interval except the first and last contains two estimates, one too high and one too low, so the resulting estimate will be more accurate.
  ::Parabolas随后通过图上每组三个连续点来构造。下图显示了前三组 n=6次间距的参数。可以看到,除第一个和最后一个间隔外,每个间隔都包含两个估计数,一个太高,一个太低,因此得出的估计数将更准确。

  

  播放段落

  Using parabolas in this way produces the following estimate of the area from Simpson’s Rule:
  ::使用parabolas这样根据辛普森规则对面积作出以下估计:

  播放段落

  $$\begin{align*}\int \limits_a^b f(x)dx \approx \frac{\triangle x}{3}[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4) \ldots + 2f(x_{n-2})+4f(x_{n-1})+f(x_n)].\end{align*}$$
  ::+2f(x3)+2f(x3)+2f(x4)。+2f(xn-2)+4(xn-1)+4f(xn-1)+f(xn)]。

  播放段落

  We see that it has a similar appearance to the Trapezoidal Rule. However, there is one distinction we need to note. The process of using three consecutive $\begin{align*}x_i\end{align*}$ to approximate parabolas will require that we assume that  $\begin{align*}n\end{align*}$ must always be an even number.
  ::我们发现,它与《特雷帕多瓦规则》的外观相似,然而,我们需要指出一个区别。 使用连续三步的xi来接近parabolas的过程要求我们假设n必须始终是偶数。

  播放段落

  Error Estimates for Simpson’s Rule
  ::辛普森规则的错误估计

  播放段落

  As with the Trapezoidal Rule, we have a formula that suggests how we can choose  $\begin{align*}n\end{align*}$ to ensure that the errors are within acceptable boundaries. The following method illustrates how we can choose a sufficiently large $\begin{align*}n\end{align*}$ .
  ::与《轨迹规则》一样,我们有一个公式,建议我们如何选择 n 以确保错误在可接受的边界内。以下方法说明了我们如何选择足够大的 n 。

  播放段落

  Suppose $\begin{align*}|f^4(x)| \le k\end{align*}$ for $\begin{align*}a \le x \le b\end{align*}$ . The error estimate is then given by
  ::axb 假设 f4(x)k。 错误估计由

  播放段落

  $$\begin{align*}|Error_{simpson}| \le \frac{k(b-a)^5}{180 \ n^4}. \end{align*}$$
  ::orrorsimpsonk(b-a)5180 n4。

  播放段落

  Apply the information above and use Simpson’s Rule to approximate $\begin{align*}\int\limits_1^4 \frac{1}{x} dx\end{align*}$ with $\begin{align*}n = 6\end{align*}$ .
  ::适用上述信息,并使用辛普森规则,以约411xdxx和n=6。

  播放段落

  We find $\begin{align*}\triangle x = \frac{b - a}{n} = \frac{4 - 1}{6} = \frac{1}{2}\end{align*}$ .
  ::我们发现X=b -an=4 -16=12

  播放段落

  $$\begin{align*}\int \limits_1^4 \frac{1}{x}dx & \approx \frac{1}{6} \left[f(1) + 4f \left(\frac{3}{2}\right) + 2f(2) + 4f \left(\frac{5}{2}\right) +2f(3) + 4f \left(\frac{7}{2}\right) +f(4)\right] \\ &= \frac{1}{6}\left[1+ \left(4 \cdot \frac{2}{3}\right) + \left(2 \cdot \frac{1}{2}\right) + \left(4 \cdot \frac{2}{5}\right) + \left(2 \cdot \frac{1}{3}\right)+ \left(4 \cdot \frac{2}{7}\right)+ \frac{1}{4}\right] \\ &= \frac{1}{6} \left[\frac{3517}{420}\right]=1.3956. \end{align*}$$
  ::411xdx16[f(1)+4f(32)+2f(2)+4f(52)+2f(3)+4f(72)+4f(4)]=16[1+(423)+(212)+(425)+(213)+(427)+14]=16[3517420]=1.3956。

  播放段落

  This turns out to be a pretty good estimate, since we know that
  ::事实证明这是一个很好的估计,因为我们知道

  播放段落

  $$\begin{align*}\int \limits_1^4 \frac{1}{x}dx =\ln x \Bigg]_1^4 = \ln(4) - \ln(1)=1.3863.\end{align*}$$
  ::411xdx=lnx41=ln(4)-ln(1)=1.3863。

  播放段落

  Therefore the error is less than 0.01.
  ::因此,错误小于0.01。

  播放段落

  Examples 
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if you think that using parabolas to estimate the would give a more accurate estimate than using trapezoids. Can you think of any reason why the concavity of the function curve would matter in the accuracy of the area estimation using parabolas?
  ::早些时候,有人问您是否认为使用parabolas来估算这些数值比使用parapezoids更准确。 你能想到为什么使用parabolas来计算区域估计的准确性取决于函数曲线的精度吗?

  播放段落

  If you think that the use of parabolas to fit the function curve would give a more accurate result (with number of subintervals the same) you are correct. With some examples, you can see visually that the overlapping parabolas fit the function curve better than line segment, and therefore the area under the curve. The parabolas do a better job than trapezoids addressing the concavity of the function curve.
  ::如果您认为使用 parabolas 来匹配函数曲线会给出一个更准确的结果( 与次对数相同) , 您是正确的 。 举例来说, 您可以看到, 重叠的 parabolas 与函数曲线的曲线比线条段更匹配, 因而也比曲线下的区域更匹配。 parbolas 比处理函数曲线精度的插件更好的工作 。

  播放段落

  Example 2
  ::例2

  播放段落

  Find $\begin{align*}n\end{align*}$ so that the Simpson Rule Estimate for $\begin{align*}\int\limits_1^4 \frac{1}{x} dx\end{align*}$ is accurate to 0.001.
  ::查找 n 这样辛普森规则估计 411xdx 准确到0.001。

  播放段落

  We need to find  $\begin{align*}n\end{align*}$ such that $\begin{align*}|Error_{simpson}| \le 0.001\end{align*}$ .
  ::我们需要找到一个能 达到0.001的错误的答案

  播放段落

  We start by noting that $\begin{align*}|f^4(x)|=\left|\frac{24}{x^5}\right|\end{align*}$ for $\begin{align*}1 \le x \le 4\end{align*}$ . Hence we can take $\begin{align*}k = 24\end{align*}$ to find the error bound:
  ::我们首先指出, 1 =x} = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

  播放段落

  $\begin{align*}\left|Error_{simpson}\right| \le \frac{24(4-1)^5}{180 \ n^4}=\frac{5832}{180 \ n^4}.\end{align*}$
  ::24(4-1)5180 n4=5832180 n4。

  播放段落

  Hence we need to solve the following inequality for $\begin{align*}n\end{align*}$ :
  ::因此,我们需要解决n的以下不平等问题:

  播放段落

  $\begin{align*}\frac{5832}{180 \ n^4}< 0.001.\end{align*}$
  ::5832180 n4<0.001。

  播放段落

  We find that :
  ::我们认为:

  播放段落

  $\begin{align*}n^4 > \frac{5832}{180(0.001)}\end{align*}$ , so that $\begin{align*}n > \sqrt[4] {\frac{5832}{180(0.001)}} \approx 13.42\end{align*}$ .
  ::n4>5832180(0.001),因此 n>45832180(0.0001)13.42。

  播放段落

  Hence we must take $\begin{align*}n = 14\end{align*}$ to achieve the desired accuracy.
  ::因此,我们必须以n=14达到预期的准确度。

  播放段落

  Example 3
  ::例3

  播放段落

  Use Simpson’s Rule to approximate $\begin{align*}\int \limits_0^2 {x^3}dx\end{align*}$ for $\begin{align*}n = 4\end{align*}$ . Round the answer to four decimal places and compare this value to the exact value of the integral. What is the expected error for $\begin{align*}n = 4\end{align*}$ ?
  ::使用辛普森规则, n=4 大约为 20x3dx 。 将答案四舍五入到小数点后四位, 并将这个值与积分的准确值进行比较。 N=4 的预期错误是什么?

  播放段落

  We find each subinterval as $\begin{align*}\triangle x = \frac{b - a}{n} = \frac{2 - 0}{4} = \frac{1}{2}\end{align*}$ .
  ::我们发现每个次interval 以 x=b -an=2 -04=12 表示 。

  播放段落

  The integral approximation is evaluated as follows:
  ::对整体近似值的评估如下:

  播放段落

  $$\begin{align*}\int_0^2 {{x^3}dx} & \approx \frac{2}{{12}}\left[ {f(0) + 4f(0.5) + 2f(1) + 4f(1.5) + f(2)} \right] \\ & \approx \frac{1}{6}\left[ {0 + 4 \cdot 0.125 + 2 \cdot 1 + 4 \cdot 3.375 + 8} \right] \\ \int_0^2 x^3 dx & \approx 4\end{align*}$$
  ::=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  The estimate of the integral is 4.
  ::综合体估计数为4。

  播放段落

  The exact value of the integral: $\begin{align*}\int\limits_0^2 x^3 dx = \frac{x^4}{4} \Bigg |_0^2 = 4\end{align*}$ .
  ::积分的准确值: 20x3dx=x44=20=4。

  播放段落

  The error between these is 0.
  ::这两者之间的错误是 0 。

  播放段落

  The expected error using $\begin{align*}n = 4\end{align*}$ :
  ::使用 n=4 的预期错误 :

  播放段落

  For fourth order derivative $\begin{align*}f^4 (x) = 0\end{align*}$ , means $\begin{align*}|Error_{Simpson}| \le \frac{0(b - a)^3}{12 \ n^2} = 0\end{align*}$ .
  ::对于第四顺序衍生物 f4(x)=0, 表示“ErrorSimpson”=0(b-a)312 n2=0。

  播放段落

  Example 4
  ::例4

  播放段落

  Use Simpson’s Rule to approximate $\begin{align*}\int \limits_1^2 \frac{1}{(x + 1)^2} dx\end{align*}$ for $\begin{align*}n = 4\end{align*}$ . Round the answer to four decimal places and compare this value to the exact value of the integral. What is the expected error for $\begin{align*}n = 4\end{align*}$ ?
  ::N=4 使用辛普森规则大约为 211 (x+1)2dx 。 将答案四舍五入到小数点后四位位数, 并将这个值与整体值的准确值进行比较。 n=4 的预期错误是什么 ?

  播放段落

  We find each subinterval as $\begin{align*}\triangle x = \frac{b - a}{n} = \frac{2 - 1}{4} = \frac{1}{4}\end{align*}$ .
  ::我们发现每个次interval 都为 x=b -an=2 -14=14。

  播放段落

  The integral approximation is evaluated as follows:
  ::对整体近似值的评估如下:

  播放段落

  $$\begin{align*}\int \limits_1^2 \frac{1}{(x + 1)^2}dx & \approx \frac{1}{12}\left[f(2) + 4f(2.25) + 2f(2.5) + 4f(2.75) + f(3)\right] \\ \int \limits_1^2 \frac{1}{(x + 1)^2}dx & \approx \frac{1}{12}\left[f(2) + 4f(2.25) + 2f(2.5) + 4f(2.75) + f(3)\right] \\ & \approx \frac{1}{12}\left[\frac{1}{4} + 4 \frac{1}{2.25^2} + 2 \frac{1}{2.5^2} + 4 \frac{1}{2.75^2} + \frac{1}{3^2} \right] \\ & \approx \frac{1}{{12}}\left[0.25 + 0.79012 + 0.32 + 0.52893 + 0.11111\right] \\ \int \limits_1^2 \frac{1}{(x + 1)^2}dx & \approx 0.16668 \approx 0.1667\end{align*}$$
  ::211(x+1)2dx112[f(2)+4f(2. 25)+2f(2.5)+4f(2. 75+f(3))]211(x+1)2dx11(x+1)2}11(x+1)2dx11[f(2)+4f(2. 25)+2(2.5)+2(2.5)+4f(2. 75)+f(3)}}112[14+412.252+212.52.52+412. 752+132]112[0.25+0. 79012+0. 32+0. 52893+0.111111]2}\\(x+1)2dx@1.668_0. 16667]

  播放段落

  The estimate of the integral is 0.1667.
  ::积分估计数为0.1667。

  播放段落

  The exact value of the integral: $\begin{align*}\int \limits_1^2 \frac{1}{(x + 1)^2}dx = \frac{-1}{x + 1} \bigg|_1^2 = \frac{1}{6} = 0.1 \overline 6\end{align*}$ .
  ::积分的准确值 : 211( x+1) 2dx% 1x+1 @ 21=16=0. 1 =6 。

  播放段落

  The error between these is 0.00001.
  ::这两者之间的错误是 0.0001 。

  播放段落

  The expected error using $\begin{align*}n = 4\end{align*}$ :
  ::使用 n=4 的预期错误 :

  播放段落

  For $\begin{align*}f^4(x) = \frac{120}{(x + 1)^6}\end{align*}$ , $\begin{align*}f^{{\prime}{\prime}}(x) \le \frac{120}{(1 + 1)^6} = \frac{15}{8} = 1.875\end{align*}$ in the interval [1, 2].
  ::F4(x) = 120(x+1) 6, f(x) 120(1+1) 6= 158= 1. 875 间隔[1, 2] 。

  播放段落

  Therefore, $\begin{align*}|Error_{Trapezoidal}| \le \frac{k(b - a)^5}{180 \ n^4} = \frac{1.875(1)^5}{180 \cdot 4^4} = 0.00004\end{align*}$ .
  ::因此,“误杀”k(b-a)5180n4=1.875(1)5180-44=0.0004。

  播放段落

  The actual error is less than $\begin{align*}|Error_{Trapezoidal}|\end{align*}$ .
  ::实际误差小于 'Error Trapezodal' 。

  播放段落

  Review
  ::回顾

  播放段落

  Use the Simpson’s Rule to approximate the definite integrals using the given number of subintervals $\begin{align*}n\end{align*}$ .
  ::使用辛普森规则,使用给定数量的次隔热量 n 来接近确定的整体体。

  播放段落
  1. $\begin{align*}\int \limits_1^7 (x + 7) dx\end{align*}$ with $\begin{align*}n = 6\end{align*}$ .
     ::71(x+7)dx, n=6。
  播放段落
  2. $\begin{align*}\int \limits_{-2}^2 (x + 4) dx\end{align*}$ with $\begin{align*}n = 4\end{align*}$ .
     ::2(x+4)dx 带有 n=4 。
  播放段落
  3. $\begin{align*}\int \limits_{-4}^1{(-x^2-2x+8)} dx\end{align*}$ with  $\begin{align*}n = 4\end{align*}$ .
     ::4 (- x2-2x+8) dx, n=4。
  播放段落
  4. $\begin{align*}\int \limits_0^2 x^3 dx\end{align*}$ for $\begin{align*}n = 8\end{align*}$ .
     ::n=8 的 0. 0x3dx
  播放段落
  5. $\begin{align*}\int \limits_0^2 {x^4} dx\end{align*}$ with $\begin{align*}n = 4\end{align*}$ .
     ::2 0x4dx 带有 n=4 。
  播放段落
  6. $\begin{align*}\int \limits_2^7 \frac{2}{x} dx\end{align*}$ with  $\begin{align*}n = 4\end{align*}$ .
     ::722xxxx与n=4。
  播放段落
  7. $\begin{align*}\int \limits_0^1 \sin{x^2} dx\end{align*}$ with $\begin{align*}n = 4\end{align*}$ .
     ::1xx2dx和 n=4。
  播放段落
  8. $\begin{align*}\int \limits_2^4 \sqrt{x} dx\end{align*}$ with $\begin{align*}n = 4\end{align*}$ .
     ::420xxxxx和n=4。
  播放段落
  9. $\begin{align*}\int \limits_0^1 x^2 e^{- x}dx\end{align*}$ with $\begin{align*}n = 8\end{align*}$ .
     ::0x2e-xdx, n=8 。
  播放段落
  10. $\begin{align*}\int \limits_1^4 \ln \sqrt{x} dx\end{align*}$ with $\begin{align*}n = 6\end{align*}$ .
      ::41lnxdx与 n=6 。
  播放段落
  11. $\begin{align*}\int \limits_0^1 \sqrt{1+x^4} dx\end{align*}$ with  $\begin{align*}n = 4\end{align*}$ .
      ::1 01+x4dx和n=4。
  播放段落
  12. $\begin{align*}\int \limits_0^2 \frac{1}{\sqrt{1+x^4}} dx\end{align*}$ with $\begin{align*}n = 6\end{align*}$ .
      ::N=6, 2011+x4dx。
  播放段落
  13. Find a value of $\begin{align*}n\end{align*}$ that guarantees an error of no more than $\begin{align*}10^{- 5}\end{align*}$ in the Simpson’s Rule approximation of $\begin{align*}\int \limits_2^4 \sqrt{x} dx\end{align*}$ .
      ::找到n的值, 保证辛普森规则近似值 42xdx 中误差不超过 10- 5 。
  播放段落
  14. How large should $\begin{align*}n\end{align*}$ be so that the Simpson’s Rule estimate for $\begin{align*}\int \limits_1^3 \frac{1}{x} dx\end{align*}$ is accurate to within 0.001?
      ::辛普森规则对 311xdx的估算准确到0.001之内,

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。