6.10 应用:概率和概率密度功能

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节应用:概率和概率密度功能

  折叠 展开

  应用:概率和概率密度功能

  播放段落

  Probability is a concept that is a familiar part of our lives. We use probability as the measure that some event (in a set of possible events) will actually occur. The set of possible events might be finite and therefore be termed a discrete random variable, or infinite and constitute a continuous random variable. A probability, $\begin{align*}P\end{align*}$ , is a number such that $\begin{align*}0\le P \le 1\end{align*}$ . The closer $\begin{align*}P\end{align*}$ is to 0, the more unlikely it is that the event will occur; the closer  $\begin{align*}P\end{align*}$ is to 1, the more likely it is that the event will occur. Also, the sum of all probabilities covering all possible events in the set, must add to 1. Can you determine before we start which type of random variable (discrete or continuous) would be associated with probabilities computed using definite integrals? Why?
  ::概率是一个我们生活中熟悉的部分概念。 我们用概率来衡量某些事件( 在一系列可能的事件中)会实际发生的概率。 一系列可能的事件可能是有限的, 因此可能的事件可能被称为一个离散随机变量, 或者无限, 并且构成一个连续随机变量。 概率, P, 是一个数值, 这样的数值是 0 P1 。 P 越接近 0 , 事件就越不可能发生; P 越接近 1 , 事件会发生的可能性就越大。 另外, 包含集中所有可能事件的所有概率的总和, 必须加上 1 。 您能否在我们开始之前确定哪类随机变量( 混杂或连续的) 会与使用确定的组成部分计算概率相联系? 为什么?

  播放段落

  Probability Density Functions
  ::概率密度函数

  播放段落

  In this section, we will look at how to compute the value of a probability by using a function called a probability density function (pdf). There are many different forms of probability density functions, and we will look at a few.
  ::在本节中,我们将研究如何使用一个称为概率密度函数(pdf)的函数来计算概率值。概率密度函数有多种不同的形式,我们将研究几个。

  播放段落

  If you were told by the postal service that you will receive a package that you have been waiting for sometime tomorrow, you might ask: What is the probability that I will receive my package sometime between 3:00 PM and 5:00 PM given that the postal service’s hours of operations are between 7:00 AM to 6:00 PM?
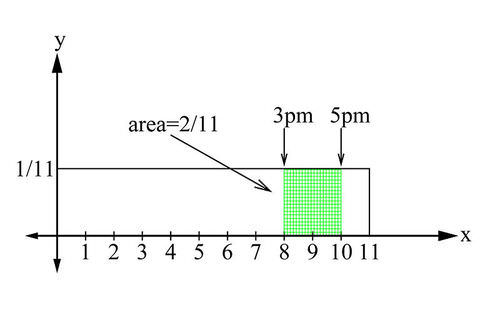
  ::如果邮局告诉您明天某天会收到您一直在等待的包裹, 您可能会问:鉴于邮局的营业时间是早上7点到下午6点之间, 那么在下午3点到下午5点之间,

  播放段落

  In the absence of any more information, one way to find a solution is to note that since the post office operates for a total of 11 hours (7 AM to 6 PM), and the interval of interest is the 2 hours between 3 PM and 5 PM, the probability that your package will arrive might just be
  ::在没有任何更多资料的情况下,找到解决办法的一个办法就是指出,由于邮局总共运作11小时(上午7时至下午6时),而利息的间隔是下午3时至5时之间的2小时,因此,你的包裹抵达的可能性可能只是

  播放段落

  $\begin{align*}P=\frac{2 \ \text{hours}}{11 \ \text{hours}}=0.182\end{align*}$
  ::P=2小时11小时=0.182

  播放段落

  So there is a probability of 0.182 that the postal service will deliver your package sometime between the hours of 3 PM and 5 PM. Because there was nothing special about the 3 pm to 5 pm interval, the 0.182 probability could apply to any 2-hour interval during the 11-hour period of operation. This also means that there is a probability of 0.818 that the package will not be delivered during that interval (i.e., 1-0.182).
  ::因此,邮政服务在下午3点到下午5点之间的某个时间会交付您的包裹的概率为0.182。由于下午3点到下午5点的间隔没有什么特别之处,因此0.182的概率可以适用于11小时运行期间的任何2小时间隔。这还意味着该包裹在该间隔期间(即1-0.182)不会交付的概率为0.818。

  播放段落

  But, mathematically, how does the above calculation standup when the 11-hour interval and the 2-hour interval contain an infinite number of times? How can one infinitydivided by another infinity produce a probability of 0.182? (Note: The possible delivery times in the 11-hour interval represent a continuous random variable.) To resolve this issue, we can represent the probability of delivery of the package at any time in the 11-hour interval as being defined by a rectangle of height $\begin{align*}\frac{1}{11}\end{align*}$  and length 11, with resulting area equal to 1. Looking at the 2-hour interval, we can see that it is equal to  $\begin{align*}\frac{2}{11}\end{align*}$  of the total rectangular area of 1. This is why it is therefore convenient to represent probabilities as areas.
  ::但是,从数学上看,当11小时间隔和2小时间隔中含有无限次数时,上述计算是站立的吗?一个以另一个无穷度分解的无穷度如何产生0.182的概率? (注:11小时间隔中可能的交货时间代表一个连续随机变量。 )为了解决这个问题,我们可以代表包件在11小时间隔中的任何时间交付的概率,这个间隔由高度111和11长度的矩形所定义,因此区域等于1。 看一下2小时间隔,我们可以看到它等于1号矩形区域总面积的211。 因此,将概率作为区域来表示是方便的。

  

  播放段落

  Since areas can be defined by definite integrals, we can also define the probability of an event occuring within an interval  $\begin{align*}[a,\ b]\end{align*}$ by the definite integral $\begin{align*}P(a\le x \le b)=\int\limits _a^b f(x)dx\end{align*}$ where  $\begin{align*}f(x)\end{align*}$  is called the probability density function (pdf).
  ::由于区域可以由确定的整体体来界定,我们也可以确定一个事件发生在一个间隔[a, b]之内的概率,由确定的整体P(axb)=baf(x)dx,其中f(x)称为概率密度函数(pdf)。

  播放段落

  A function $\begin{align*}f(x)\end{align*}$  is called a probability density function if
  ::函数 f(x) 被称为概率密度函数, 如果

  播放段落
  1. $\begin{align*}f(x)\ge 0\end{align*}$ for all $\begin{align*}x\end{align*}$
     :xx)0 全部xx
  播放段落
  2. The area under the graph of  $\begin{align*}f(x)\end{align*}$ over all the real line is exactly 1
     ::所有真实线的 f(x) 图形下区域是 1
  播放段落
  3. The probability that  $\begin{align*}x\end{align*}$ is in the interval $\begin{align*}[a,\ b] \end{align*}$ is
     ::x 在 [a、b] 间隔中的概率

  播放段落

  $\begin{align*}P(a\le x \le b)=\int\limits _a^b f(x)dx\end{align*}$
  ::P(axb) =baf(xx) dx

  播放段落

  i.e., the area under the graph of  $\begin{align*}f(x)\end{align*}$ from  $\begin{align*}a\end{align*}$ to $\begin{align*}b\end{align*}$ .
  ::i.,即 f(x) 图形下从 a 到 b.

  播放段落

  In the problem above, the probability density function $\begin{align*}f(x)\end{align*}$  is called a uniform (flat) probability density function (pdf) .
  ::在上述问题中,概率密度函数f(x)称为统一(缩放)概率密度函数(pdf)。

  播放段落

  Many other probability density functions exist that when used would give a different answer to the question about the delivery time of our package.
  ::存在许多其他概率密度函数,一旦使用,将对关于我们包件交付时间的问题给出不同的答案。

  播放段落

  Suppose that after some thought and discussion with neighbors, you decide that it would be better to use a triangular probability density function as shown below for package delivery in your area. What is the probability that you will receive your package sometime between 3:00 PM and 5:00 PM?
  ::假设在与邻居进行一些思考和讨论之后,您会决定使用以下显示的三边概率密度函数在您所在区域的软件包交付中比较好。您在下午3点到下午5点之间收到您的软件包的概率是多少?

  

  播放段落

  The triangular pdf shows a variation that can be modeled as:
  ::三角形 pdf 显示的变量可以建模如下:

  播放段落

  $\begin{align*}f(x)=\begin{cases} \frac{2}{99}(x+12)-\frac{14}{99}, \ -5\le x \le 4 \\ \frac{-1}{11}(x+12)+\frac{18}{11}, \ 4\le x \le 6\\ \end{cases}\end{align*}$
  ::f(xx) 299(x+12)-1499,- 5x4-111(x+12)+1811, 4x__6

  播放段落

  Note that the pdf is 0 outside the above interval.
  ::请注意, pdf 在上述间隔之外是 0 。

  播放段落

  The probability that the package will arrive between 3 and 5 pm can be determined as
  ::包件在下午3时至5时到达的概率可确定为:

  播放段落

  $$\begin{align*}P(a\le x\le b) &=\int\limits_a^b f(x)dx \\ P(3\le x\le 5) &=\int\limits_3^5 f(x)dx \\ &=\int\limits_3^4\left(\frac{2}{99}(x+12)-\frac{14}{99}\right)dx+\int\limits_4^5\left(\frac{-1}{11}(x+12)-\frac{18}{11}\right)dx\\ &=\frac{2}{99}\left[\frac{x^2}{2}+5x \right]_3^4-\frac{1}{11}\left[\frac{x^2}{2}-6x \right]_4^5 \\ &=\frac{17}{99}+\frac{1.5}{11}\\ P(3\le x\le 5) &=\frac{30.5}{99}\approx 0.308\end{align*}$$
  ::P(axb) =baf(xx) dxP(3x) 5=53f(x) dx=43(299(x+12)-1499dx+54(-111(x+12)-1811)dx=299[x22+5x] 43-111[x22-6x] 54=1799+1.511P(3x)5)=30.599_0.308

  播放段落

  Using the triangular pdf, the probability of receiving the package between 3 and 5 pm has increased to 0.308.
  ::使用三角方块pdf, 下午3时至5时接收包件的概率增加到0.308。

  播放段落

  The Normal Probability Density Function
  ::正常概率密度函数

  播放段落

  One of the most useful probability density functions is the  normal or Gaussian probability density function (sometimes referred to as the  bell curve ) defined as:
  ::最有用的概率密度函数之一是通常或高斯概率密度函数(有时称为钟曲线),其定义为:

  播放段落

  The Gaussian curve for a population with mean  $\begin{align*}\mu\end{align*}$ and standard deviation  $\begin{align*}\sigma\end{align*}$ is given by $\begin{align*}f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{(2\sigma^2)}}\end{align*}$ , where the factor  $\begin{align*}\frac{1}{(\sigma\sqrt{2\pi})}\end{align*}$  is called the  normalization constant, which is needed to make the probability over the entire space equal to 1.
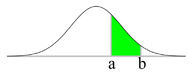
  ::f(x)=1222(x)2(2-1212)给出了平均微米和标准偏差 12 的人群的高斯曲线,其中因数(122)称为正常化常数,这是使整个空间的概率等于1所必需的。

  播放段落

  The density function has the bell curve shape represented below:
  ::密度函数的钟曲线形状如下:

  

  播放段落

  This function enables us to describe an entire population based on statistical measurements taken from a small sample of the population. The only measurements needed are the mean  $\begin{align*}(\mu)\end{align*}$ and the standard deviation $\begin{align*}(\sigma)\end{align*}$ . Once those two numbers are known, the normal curve is defined.
  ::此函数使我们能够根据从少量抽样人口中得出的统计测量结果来描述整个人口。 唯一需要测量的是平均值( 微克) 和标准偏差( 12) 。 一旦知道这两个数字, 就会定义正常曲线 。

  播放段落

  Suppose that boxes containing 100 tea bags have a mean weight of 10.2 ounces each and a standard deviation of 0.1 ounce. What percentage of all the boxes is expected to weigh between 10 and 10.5 ounces? What is the probability that a box weighs less than 10 ounces? What is the probability that a box will weigh exactly 10 ounces?
  ::假设装有100个茶袋的盒子平均重量为每块10.2盎司,标准偏差为0.1盎司。 所有盒子中,预期重量在10到10.5盎司之间的比例是多少?一个盒子的重量小于10盎司的概率是多少?一个盒子精确重量为10盎司的概率是多少?

  播放段落

  Using the normal probability density function , $\begin{align*}f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{(2\sigma^2)}}\end{align*}$ .
  ::使用正常的概率密度函数 f( x)=1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\2\\\\\\\\\\\\\\2\\\\\\

  播放段落

  Substituting for  $\begin{align*}\mu=10.2\end{align*}$  and  $\begin{align*}\sigma=0.1\end{align*}$ , we get $\begin{align*}f(x)=\frac{1}{(0.1) \sigma \sqrt{2\pi}}e^{\frac{-(x-10.2)^2}{(2(0.1)^2)}}\end{align*}$ .
  ::10.2和0.1的替代,我们得到f(x)=1(0.1)2e-(x-10.2)2(2(0.2)。

  播放段落

  The percentage of all the tea boxes that are expected to weight between 10 and 10.5 ounces can be calculated as
  ::所有茶盒中预计重量在10至10.5盎司之间的百分比可按下列方式计算:

  播放段落

  $\begin{align*}P(10\le x\le 10.5)=\int\limits_{10}^{10.5} \frac{1}{(0.1)\sqrt{2\pi}}e^{\frac{-(x-10.2)^2}{(2(0.1)^2)}dx}\end{align*}$ .
  ::P(10x10.5)=10.5101(0.1)2e-(x-10.2)2(2(0.1/2)dx。

  播放段落

  The integral of  $\begin{align*}e^{x^2}\end{align*}$ does not have an elementary anti-derivative and therefore cannot be evaluated by standard techniques. However, we can use numerical techniques, such as The Simpson’s Rule or The Trapezoid Rule, to find an approximate (but very accurate) value. Using the programming feature of a scientific calculator or, mathematical software, we eventually get $\begin{align*}\int\limits_{10}^{10.5} \frac{1}{(0.1)\sqrt{2\pi}}e^{\frac{-(x-10.2)^2}{(2(0.1)^2)}dx}\approx0.976\end{align*}$ That is, $\begin{align*}P(10\le x\le 10.5)\approx0.976\end{align*}$ .
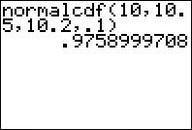
  ::Ex2的组成部分没有基本的抗变性,因此无法用标准技术进行评估。 但是,我们可以使用“辛普森规则 ” 或“轨迹规则 ” 等数字技术来找到一个近似(但非常准确)值。 使用科学计算器或数学软件的编程特征,我们最终会得到10.5101(0.1)%22e-(x-10.2)2(2(0.1.2)、dx0.976,即P(10x)10.5)0.976。

  播放段落

  Technology Note: To make this computation with a graphing calculator of the TI-83/84 family, do the following:
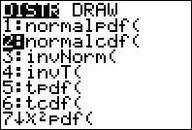
  ::技术说明:为了用TI-83/84家族的图表计算计算器进行计算,请做以下工作:

  播放段落

  From the [DISTR] menu (Figure 6.11.4) select option 2, which puts the phrase “normalcdf” in the home screen. Add lower bound, upper bound, mean, standard deviation, separated by commas, close the parentheses, and press [ENTER] . The result is shown in Figure 6.11.5.
  ::从[DISTR]菜单(图6.1.1.4)中选择选项2,在主屏幕上加上“uscdf”一语。添加下下框、上框、平均值、标准差、用逗号分隔、关闭括号、按下[ENTER]。结果见图6.1.1.5。

  

  

  播放段落

  For the probability that a box weighs less than 10.2 ounces, we use the to the left of $\begin{align*}x=10.2\end{align*}$ .
  ::对于一个盒子重量小于10.2盎司的概率,我们用 x=10.2 的左方。

  播放段落

  Integrating numerically , we get
  ::以数字集成,我们得到

  播放段落

  $$\begin{align*}P(9\le x\le 10) &=\int\limits_9^{10}\frac{1}{(0.1)\sqrt{2\pi}}e^{\frac{-(x-10.2)^2}{(2(0.1)^2)}dx}\\ P(9\le x\le 10.2) & \approx 0.02275\\ &=2.28\%, \end{align*}$$
  ::P(9x10)=1091(0.1)2e-(x-10.2)2(2(0.1.2),dxP(9x10.2)0.02275=2.28%,

  播放段落

  which says that we would expect 2.28% of the boxes to weigh less than 10 ounces.
  ::也就是说,我们预计2.28%的箱子重量 低于10盎司。

  播放段落

  Theoretically the probability here will be exactly zero because we will be integrating from 10 to 10 which is zero. However, since all scales have some error (call it  $\begin{align*}\epsilon\end{align*}$ ), practically we would find the probability that the weight falls between $\begin{align*}10-\epsilon\end{align*}$ and  $\begin{align*}10+\epsilon\end{align*}$ .
  ::从理论上讲,这里的概率将是零,因为我们将从10到10融合到零。然而,由于所有尺度都存在一些错误(叫它 ) , 实际上我们会发现重量在10到10之间的概率。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to determine which type of random variable (discrete or continuous) would be associated with probabilities computed using definite integrals.
  ::早些时候,有人要求你确定哪类随机变量(分辨或连续的)与使用确定的组成部分计算的概率有关。

  播放段落

  If you said that the continuous random variable would be associated with probabilities determined by definite integrals, you would be correct.
  ::如果你说连续随机变数 与确定的整体体确定的概率有关, 你会是正确的。

  播放段落

  Example 2
  ::例2

  播放段落

  An Intelligence Quotient or IQ is a score derived from different standardized tests attempting to measure the level of intelligence of an adult human being. The average score of the test is 100 and the standard deviation is 15. What is the percentage of the population that has a score between 85 and 115? What percentage of the population has a score above 140?
  ::情报引号或IQ是试图衡量成年人智力水平的不同标准测试得出的分数,平均评分为100,标准偏差为15,85至115之间的人口百分比是多少?人口分数超过140的人口百分比是多少?

  播放段落

  Using the normal probability density function, $\begin{align*}f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{(2\sigma^2)}}\end{align*}$ , and substituting  $\begin{align*}\mu=100\end{align*}$  and  $\begin{align*}\sigma=15\end{align*}$ , $\begin{align*}f(x)=\frac{1}{15 \sqrt{2\pi}}e^{\frac{-(x-100)^2}{(2(15)^2)}}\end{align*}$ .
  ::使用正常概率密度函数 f(x) = 1 22 e- (x) 2(2- 1212) 替换 100 和 15 f(x) = 1152 e- (x) - 1002( 15) 。

  播放段落

  The percentage of the population that has a score between 85 and 115 is $\begin{align*}P(85\le x \le 115)=\int\limits_{85}^{115}\frac{1}{15 \sqrt{2\pi}}e^{\frac{-(x-100)^2}{(2(15)^2)}}\end{align*}$ .
  ::得分在85至115之间的人口百分比为P(85x115)=115851152e-(x-100)(2(15/2)。

  播放段落

  Again, the integral of  $\begin{align*}e^{-x^2}\end{align*}$  does not have an elementary anti-derivative and therefore cannot be evaluated. Using the programing feature of a scientific calculator or a mathematical computer software, we get $\begin{align*}\int\limits_{85}^{115}\frac{1}{15 \sqrt{2\pi}}e^{\frac{-(x-100)^2}{(2(15)^2)}}dx\approx0.68\end{align*}$ . That is, $\begin{align*}P(85\le x \le 115)\approx 68\%\end{align*}$
  ::同样,e-x2的有机体没有基本的抗降解性,因此无法评估。使用科学计算器或数学计算机软件的编程功能,我们得到1158511225-(x-100)(2(2(152(152)dx0.68),即P(85x115)68%。

  播放段落

  Which says that 68% of the population has an IQ score between 85 and 115.
  ::也就是说,68%的人口的智商分数在85至115之间。

  播放段落

  To measure the probability that a person selected randomly will have an IQ score above 140, $\begin{align*}P(x\ge 140)=\int\limits_{140}^{\infty}\frac{1}{15 \sqrt{2\pi}}e^{\frac{-(x-100)^2}{(2(15)^2)}}dx\end{align*}$ .
  ::为衡量随机选择的人智商分数超过140的概率,P(x140)14011152e-(x-1002(2(152)dx)。

  播放段落

  This integral is even more difficult to integrate since it is an improper integral . To avoid the messy work, we can argue that since it is extremely rare to meet someone with an IQ score of over 200 we can approximate the integral from 140 to 200 Then $\begin{align*}P(x\ge 140)=\int\limits_{140}^{200}\frac{1}{15 \sqrt{2\pi}}e^{\frac{-(x-100)^2}{(2(15)^2)}}dx\end{align*}$ .
  ::这个整体体更难整合,因为它是一个不适当的整体体。 为了避免混乱的工作,我们可以争辩说,由于与智商超过200分的人见面极为罕见,我们可以在140到200分之间接近综合体,然后是P(x)140=2001401115/2e-(x)-1002(2((152))dx。

  播放段落

  Integrating numerically, we get $\begin{align*}P(x\ge 140)\approx 0.0039\end{align*}$ .
  ::从数字上整合,我们得到P(x)140) 0.0039。

  播放段落

  So the probability of selecting at random a person with an IQ score above 140 is 0.0039. That’s about one person in every 250 individuals!
  ::因此随机选择智商得分超过140的人的概率是0.0039。 每250人中大约有一人!

  播放段落

  Review
  ::回顾

  播放段落

  For #1-4, find the number $\begin{align*}r\end{align*}$  that makes the function a probability density function over the given sample space.
  ::对于 # 1-4, 找到使该函数在给定样本空间上成为概率密度函数的数字 r。

  播放段落
  1. $\begin{align*}f(x)=r\end{align*}$ over the sample space of [-7, 7].
     ::f(x)=r 超过[7、7]的样本空间。
  播放段落
  2. $\begin{align*}f(x)=rx(x-5)\end{align*}$ over the sample space of [0, 5].
     ::f(x)=[0,5]样本空间之上的rx(x-5)。
  播放段落
  3. $\begin{align*}f(x)=\frac{r}{(1+x)^2}\end{align*}$ over the sample space of [0, 25].
     ::f(x)=r(1+x)2,超出[0, 25]的样本空间。
  播放段落
  4. $\begin{align*}f(x)=r\sin x\end{align*}$ over the sample space of $\begin{align*}\left[0,\ \frac{\pi}{2}\right ]\end{align*}$ .
     ::f(x)=在[0] +2的样本空间之上的rrinx。
  播放段落
  5. Given a triangular probability density function $\begin{align*}g(x)\end{align*}$  over the sample space [0, 10], what is the highest value of $\begin{align*}g(x)\end{align*}$  if it occurs at $\begin{align*}x=7\end{align*}$ ?
     ::鉴于在样本空间[0, 10] 上方的三角概率密度函数g(x),如果在 x=7时发生,g(x)的最高值是多少?
  播放段落
  6. Could the function $\begin{align*}g(x)=\frac{-4}{25}x+0.9\end{align*}$  be a probability density function over the interval [0, 10]?
     ::函数 g( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以概率密度的概率密度密度密度密度密度密度密度密度密度密度密度密度密度密度密度密度的概率密度密度密度密度密度密度密度密度密度密度密度的概率密度密度密度的概率密度的概率密度密度的概率密度密度的[[1010101010??????????????????????????????????????????10???????????????????????\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
  播放段落
  7. Suppose  $\begin{align*}f(x)\end{align*}$  is the probability density function for the lifetime of a manufacturer’s light bulb, where  $\begin{align*}x\end{align*}$  is measured in hours. Explain the meaning of each integral.
     播放段落
     1. $\begin{align*}\int\limits_{1000}^{5000}f(x)dx\end{align*}$
        ::50001000f(x)dx
     播放段落
     2. $\begin{align*}\int\limits_{3000}^{\infty}f(x)dx\end{align*}$
        ::3000f( x) dx
     
     ::假设 f( x) 是制造商灯泡寿命周期的概率密度函数, 该灯泡按小时测量 x。 解释每个组件的含义 。 5000\\\ 10000 f( x) dx = 3000 f( x) dx
  播放段落
  8. Suppose $\begin{align*}f(x)=-\frac{1}{36}(x^2-9)\end{align*}$  is the probability density function for an event’s time of occurrence within the time window [-3, +3 hours] (0 is on time occurrence). What is the probability the event occurs within $\begin{align*}\pm 1\end{align*}$  hour of the expected time?
     ::假设 f( x)\\ 136( x2- 9) 是时间窗口 [ 3, + 3 小时] ( 0) 内事件发生时间的概率密度函数 。 事件发生在预期时间 + 1 小时之内的概率是多少 ?
  播放段落
  9. For problem #8, what time window guarantees a 90% probability of occurrence?
     ::对于问题8, 什么时间窗口能保证90%的发生概率?
  播放段落
  10. The length of time a customer spends waiting until his/her entree is served at a certain restaurant is modeled by an exponential density function $\begin{align*}f(x)=0.125e^{-0.125t}\end{align*}$ , where $\begin{align*}\frac{1}{0.125}=8\end{align*}$ is the average wait time in minutes.
      播放段落
      1. What is the probability that a customer is served in the first 3 minutes?
         ::客户在前3分钟就被送达服务的可能性有多大?
      播放段落
      2. What is the probability that a customer has to wait more than 10 minutes?
         ::顾客等10分钟以上的可能性有多大?
      
      ::客户在某一餐馆等候其主菜服务的时间长度以指数密度函数f(x)=0.125e-0.125t为模型,其中10.125=8是每分钟的平均等候时间。客户在头3分钟服务的可能性是多少?客户需要等待10分钟以上的概率是多少?
  播放段落
  11. The average height of an adult female in Los Angeles is 63.4 inches (5 feet, 3.4 inches) with a standard deviation of 3.2 inches.
      播放段落
      1. What is the probability that a female’s height is less than 63.4 inches?
         ::女性身高低于63.4英寸的概率是多少?
      播放段落
      2. What is the probability that a female’s height is between 63 and 65 inches?
         ::女性身高在63至65英寸之间的概率有多大?
      播放段落
      3. What is the probability that a female’s height is more than 6 feet?
         ::女性身高超过6英尺的概率有多大?
      播放段落
      4. What is the probability that a female’s height is exactly 5 feet?
         ::女性身高的几率是5英尺?
      
      ::在洛杉矶,成年女性的平均身高为63.4英寸(5英尺,3.4英寸),标准偏差为3.2英寸。 女性身高低于63.4英寸的概率是多少?女性身高在63至65英寸之间的概率是多少?女性身高超过6英尺的概率是多少?女性身高完全5英尺的概率是多少?
  播放段落
  12. The  median of a distribution with a probability density function $\begin{align*}f(x),\end{align*}$ is the value $\begin{align*}M\end{align*}$  such that $\begin{align*}\int \limits_{-\infty }^{M}f(x)dx=0.5\end{align*}$ . Half the values of the distribution will be above $\begin{align*}M\end{align*}$ , and half will be below $\begin{align*}M\end{align*}$ . Find the median value for each of the following probability density functions:
      播放段落
      1. $\begin{align*}f(x)=-\frac{1}{36}(x^2-9)\end{align*}$ over the interval [-3, 3].
         ::f(x)136(x2-9)间隔[-3,3]。
      播放段落
      2. $\begin{align*}f(x)=0.125e^{-0.125t}\end{align*}$ over the interval $\begin{align*}[0,\ \infty)\end{align*}$ .
         ::f(x) = 0.125e-0.125t 间隔 [0, ] 。
      
      ::具有概率密度函数 f(x) 的分布中值为 M 值,即 Mf(x)dx=0.5.5。 分布值的一半将高于 M, 一半将低于 M。 查找下列概率密度函数的中值 : f(x)\ 136(x2-9) 间距[ 3, f(x) =0.125e-0.125t 间距 [0, ] 。
  播放段落
  13. The mean of a distribution with the probability density function $\begin{align*}f(x),\end{align*}$ is the value given by $\begin{align*}\int\limits _{-\infty}^{\infty}xf(x)dx\end{align*}$ . Find the mean value for each of the following probability density functions:
      ::概率密度函数 f( x) 的分布平均值是 xf( x) dx 给出的值。 查找下列概率密度函数的平均值 :
  播放段落
  14. 播放段落
      1. $\begin{align*}f(x)=-\frac{1}{36}(x^2-9)\end{align*}$ over the interval [-3, 3].
         ::f(x)136(x2-9)间隔[-3,3]。
      播放段落
      2. $\begin{align*}f(x)=0.125e^{-0.125t}\end{align*}$ over the interval $\begin{align*}[0,\ \infty)\end{align*}$ .
         ::f(x) = 0.125e-0.125t 间隔 [0, ] 。
      
      ::f(x)=0.125e-0.125t 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。