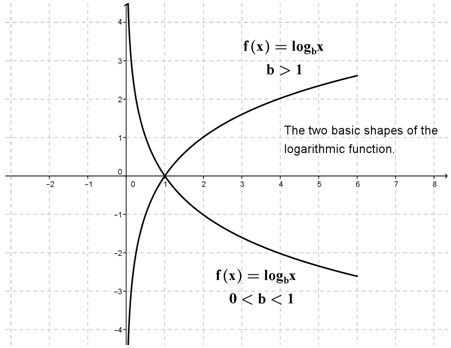Course: 7.2 指数函数和对数函数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

指数函数和对数函数

Exponential and are elementary transcendental functions that are inverses. The function $\begin{aligned} f (x) = 3^{x} \end{aligned}$ is an exponential function, and the function $\begin{aligned} g (x) = \log x \end{aligned}$ is a logarithmic function. Given your current knowledge, can you say at this point whether $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are inverses?
::指数和基本超常函数是反向的。函数 f( x) =3x 是一个指数函数, 函数 g( x) =logx 是一个对数函数。根据您目前的知识, 您可以在这一点上说 f( x) 和 g( x) 是反向函数吗 ?

Exponential and Logarithmic Functions
::指数函数和对数函数

The Exponential Function
::指数函数

An exponential function is a function of the form: $\begin{aligned} f (x) = b^{x} \end{aligned}$ , where $\begin{aligned} b \end{aligned}$ , the base , is a constant with $\begin{aligned} b > 0 \end{aligned}$ and $\begin{aligned} b \neq 1 \end{aligned}$ ; and the domain of $\begin{aligned} f \end{aligned}$ is the set of all real numbers. $\begin{aligned} f (x) \end{aligned}$ is called an exponential function with base $\begin{aligned} b \end{aligned}$ .
::指数函数是窗体的函数 : f( x) =bx, 其中 b, 基数为 b>0 和 b1 的常数; f 的域是所有实际数字的一组。 f( x) 称为 b 基数的指数函数。

Some examples are: $\begin{aligned} f (x) = 2^{x}, f (x) = {(\frac{1}{2})}^{x}, f (x) = 10^{x} \end{aligned}$ and $\begin{aligned} f (x) = e^{x} \end{aligned}$ .
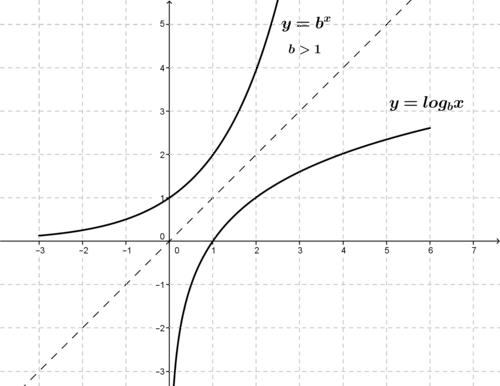
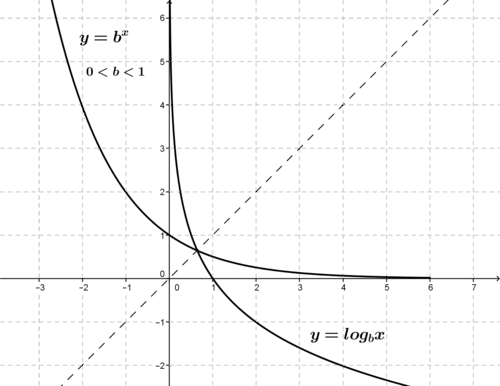
::例如:f(x)=2x,f(x)=(12)x,f(x)=10x和f(x)=ex。

All exponential functions are continuous and each has a graph that is one of the two basic shapes shown below, depending on whether $\begin{aligned} 0 < b < 1 \end{aligned}$ or $\begin{aligned} b > 1 \end{aligned}$ .
::所有指数函数都是连续的,每个函数都有一个图表,即下面显示的两种基本形状之一,取决于是0<b<1还是b>1。

Useful properties of exponential functions are summarized below.
::指数函数的有用性概述如下。

For $\begin{aligned} x \in R \end{aligned}$ , and $\begin{aligned} b \end{aligned}$ a constant with $\begin{aligned} b > 0 \end{aligned}$ and $\begin{aligned} b \neq 1 \end{aligned}$ :
::xR, 和 b 为 b>0 和 b1 的常数:

$\begin{aligned} b^{p} b^{x} = b^{(p + x)} \end{aligned}$ , $\begin{aligned} p \end{aligned}$ is a real variable/number
::bpbx=b(p+x), p 是真实的变量/ 数字

$\begin{aligned} (b^{x})^{p} = (b^{p})^{x} = b^{p x} \end{aligned}$ , $\begin{aligned} p \end{aligned}$ is a real variable/number
:xx)p=(bp)xx=bpx,p是一个真实变量/数字

$\begin{aligned} \frac{b^{x}}{b^{p}} = b^{(x - p)} \end{aligned}$
::bxbp=b(x-p)

$\begin{aligned} \sqrt[p]{b^{x}} = b^{\frac{x}{p}} \end{aligned}$ , $\begin{aligned} p \end{aligned}$ is an integer $\begin{aligned} \geq 2 \end{aligned}$
::bxp=bxp, p 是一个整数 #% 2

Inverse of the Exponential Function: The Logarithmic Function
::指数函数的反对数函数:对数函数

Because the exponential function is always increasing (for $\begin{aligned} b > 1 \end{aligned}$ ) or always decreasing (for $\begin{aligned} 0 < b < 1 \end{aligned}$ ) as shown in graphs above, the function is one-to-one, and therefore has an inverse. To find the inverse of any one-to-one function, just reflect it about the line $\begin{aligned} y = x \end{aligned}$ . Doing this for the two exponential function forms above yields the graphs below of the two corresponding . (Note these use base 2 and $\begin{aligned} \frac{1}{2} \end{aligned}$ as the examples.)The inverse of the exponential function $\begin{aligned} y = b^{x} \end{aligned}$ is called the logarithmic function, identified as $\begin{aligned} y = \log_{b} x \end{aligned}$ .
::由于指数函数总是在增加(b>1)或总是在减少(如以上图表所示,0<b<1),该函数是一对一,因此有一个反向。要找到一对一函数的反向,请在 y=x 线上反射。如果对上两个指数函数表进行反射,则得出两个对应的图形下方的图。 (注意这些用基数 2 和 12 作为示例。) y=bx 的反向函数称为对数函数,称为 y=logb+x 。

A logarithmic function is a function of the form: $\begin{aligned} f (x) = \log_{b} x \end{aligned}$ , where $\begin{aligned} b \end{aligned}$ is a constant with $\begin{aligned} b > 0 \end{aligned}$ and $\begin{aligned} b \neq 1 \end{aligned}$ ; and the domain of $\begin{aligned} f^{'} \end{aligned}$ is the set $\begin{aligned} x > 0 \end{aligned}$ . $\begin{aligned} f (x) \end{aligned}$ is called a logarithmic function with base $\begin{aligned} b \end{aligned}$ , and has the following relationship with the exponential function with base $\begin{aligned} b \end{aligned}$ : if $\begin{aligned} \log_{b} x = y \end{aligned}$ , then $\begin{aligned} b^{y} = b^{\log_{b} x} = x \end{aligned}$ .
::对数函数是窗体函数的函数 : f( x) =logb x, b是 b>0 和 b1 的常数; fä 的域是 set x>0. f( x) 。 f( x) 被称为 b b 的对数函数, 与 b 的指数函数有以下关系 : 如果logbx=y, 然后是=blogbx=x, 则与 b 的指数函数有以下关系。

Note that just like exponential functions, the logarithmic functions are continuous and each has a graph that is one of the two basic shapes shown in the graphs above and below, depending on whether $\begin{aligned} 0 < b < 1 \end{aligned}$ or $\begin{aligned} b > 1 \end{aligned}$ .
::请注意,与指数函数一样,对数函数是连续的,每个函数有一个图表,它是以上和下图中显示的两个基本形状之一,取决于是0<b<1还是b>1。

Important Properties of Logarithms
::对数的重要属性

For $\begin{aligned} b \end{aligned}$ a constant with $\begin{aligned} b > 0 \end{aligned}$ and $\begin{aligned} b \neq 1 \end{aligned}$ and $\begin{aligned} m > 0, n > 0 \end{aligned}$
::对于 b 的常数, b>0 和 b1 和 m>0, n>0

$\begin{aligned} \log_{b} 1 = 0 \end{aligned}$
::对数b=0

$\begin{aligned} \log_{b} b = 1 \end{aligned}$
::对数bb=1

$\begin{aligned} \log_{b} (m)^{r} = r \log_{b} (m) \end{aligned}$
::logb(m)r=rlogb(m)

$\begin{aligned} \log_{b} (m \cdot n) = \log_{b} m + \log_{b} n \end{aligned}$
::logb( mn) =logbm+logbn

$\begin{aligned} \log_{b} \frac{m}{n} = \log_{b} m - \log_{b} n \end{aligned}$
::logbmn=logbm-logbn

$\begin{aligned} \log_{b} m = \frac{\log_{a} m}{\log_{a} b} \end{aligned}$
::对数b=loga=mloga=mloga=b 对数b=loga=mloga=b

Exponential and Logarithmic Function Relationship
::指数和对数函数关系

For $\begin{aligned} y > 0, x \in R, \end{aligned}$ and $\begin{aligned} b > 0 \end{aligned}$ and $\begin{aligned} b \neq 1 \end{aligned}$ :
::y>0,xR,和b>0和b1:

\begin{aligned} y = b^{x} \Leftrightarrow x = \log_{b} y . \end{aligned}

::y=bxxx=logb_y。 y=bxxxxx=logb_y。 y=bxxxxxx=logb_y。

This means: for $\begin{aligned} b = 10, y = 10^{x} \Leftrightarrow x = \log y \end{aligned}$ (common log),
::这意味着: b=10,y=10xxx=logy(共同日志),

and for $\begin{aligned} b = e, y = e^{x} \Leftrightarrow x = \ln y \end{aligned}$ (natural log)
::b=e,y=exx=lny(自然日志)

Examples of the relationship between the logarithmic function form and the corresponding exponential function form are shown in the table.
::对数函数窗体与相应的指数函数窗体之间的关系实例见表格。

Logarithmic Form ::对数表	$\begin{aligned} \log_{b} x = y \end{aligned}$ ::对数bx=y	$\begin{aligned} \log_{\frac{1}{2}} 16 = - 4 \end{aligned}$ ::对数12164	$\begin{aligned} \log_{2} 16 = 4 \end{aligned}$ ::log216=4	$\begin{aligned} \log_{10} 100 = 2 \end{aligned}$ ::对数 10\\\\\100=2	$\begin{aligned} \log_{e} e = 1 \end{aligned}$ ::loge loge=1 loge loge=1 loge loge=1 loge loge=1
Exponential Form ::指数表	$\begin{aligned} b^{y} = x \end{aligned}$ ::结束时间=x	$\begin{aligned} {(\frac{1}{2})}^{- 4} = 16 \end{aligned}$	$\begin{aligned} 2^{4} = 16 \end{aligned}$	$\begin{aligned} 10^{2} = 100 \end{aligned}$	$\begin{aligned} e^{1} = e \end{aligned}$ ::e1=e

Historically, logarithms with base of 10 were very popular. They are called the common logarithms . Recently the base 2 has been gaining popularity due to its considerable role in the field of computer science and the associated binary number system. However, the most widely used base in applications is the irrational base denoted by $\begin{aligned} e \end{aligned}$ in honor of the famous mathematician Leonhard Euler. This irrational constant is $\begin{aligned} e \approx 2.718281 \end{aligned}$ , and it is defined as follows:
::历史上, 以 10 为基数的对数非常流行。它们被称为通用对数。最近, 基数 2 因其在计算机科学和相关二进制系统中的显著作用而越来越受欢迎。然而, 应用中最广泛使用的基数是非理性基数, 由著名的数学家Leonhard Euler 来表示。这个非理性常数是 e2. 718281, 定义如下:

\begin{aligned} lim_{x \to 0} (1 + x)^{\frac{1}{x}} = e . \end{aligned}

::limx0( 1+x) 1x=e.

The logarithm $\begin{aligned} \log_{e} x \end{aligned}$ is called the natural logarithm of $\begin{aligned} x \end{aligned}$ , and is denoted $\begin{aligned} \ln x \end{aligned}$ rather than $\begin{aligned} \log_{e} x \end{aligned}$ . The relationship between the natural logarithmic function and the corresponding exponential function is still the same: $\begin{aligned} y = \ln x - x = e^{y} \end{aligned}$ .
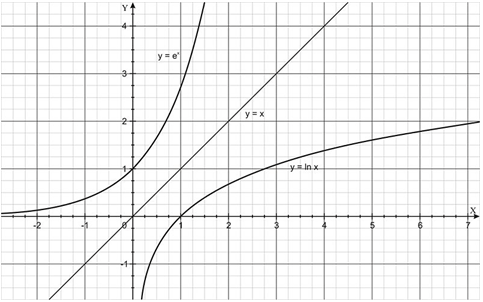
::对数对数logex 被称为x的自然对数,它表示的是inx,而不是logex。自然对数函数和相应的指数函数之间的关系保持不变:y=lnx-x=ey。

The graph and the table below shows this relationship.
::下表和图表显示了这种关系。

Logarithm Form ::对对数窗体	$\begin{aligned} \ln x = y \end{aligned}$ ::伊尼克斯=y	$\begin{aligned} \ln 2 \approx 0.693 \end{aligned}$ ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}6点93分 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}6点93分 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}6点93分 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}6点93分	$\begin{aligned} \ln 1 = 0 \end{aligned}$ ::内1=0	$\begin{aligned} \ln e = 1 \end{aligned}$ ::内=1	$\begin{aligned} \ln e^{3} = 3 \end{aligned}$ ::3=3 内3=3
Exponential Form ::指数表	$\begin{aligned} e^{y} = x \end{aligned}$ ::以 =x	$\begin{aligned} e^{0.693} \approx 2 \end{aligned}$ ::e0.6932	$\begin{aligned} e^{0} = 1 \end{aligned}$ ::e0=1	$\begin{aligned} e^{1} = e \end{aligned}$ ::e1=e	$\begin{aligned} e^{3} = e^{3} \end{aligned}$ ::e3=e3 电子3=e3

Solving problems involving Exponential and Logarithmic Functions
::涉及指数函数和对数函数的解决问题

The inverse relationship between the exponential and logarithm functions with the same base, means that problems involving one or the other function type can often be solved using the corresponding inverse function.
::具有相同基数的指数函数和对数函数之间的反比关系,意味着涉及一种或另一种函数类型的问题往往可以通过相应的反比函数来解决。

Consider the equation: $\begin{aligned} 1.7 \cdot 3^{x} = 21 \end{aligned}$ . First solve the equation for $\begin{aligned} x \end{aligned}$ and then rewrite the original equation in the form: $\begin{aligned} 3^{g (x)} = 21 \end{aligned}$ , i.e., without the factor of 1.7.
::考虑方程 : 1. 7}3x=21。先解析 x 的方程, 然后重写原方程的窗体: 3g(x)=21, 也就是说, 不包括1.7 系数。

The value of $\begin{aligned} x \end{aligned}$ is obtained by isolating the exponential function $\begin{aligned} 3^{x} \end{aligned}$ , and then using a log function:
::x 的值通过分离指数函数 3x 获得,然后使用日志函数 :

\begin{aligned} 1.7 \cdot 3^{x} & = 21 \\ 3^{x} & = \frac{21}{1.7} \\ \log (3^{x}) & = \log (\frac{21}{1.7}) \dots Here the common log is used; \\ the natural log could also have been used, \\ as well as any other log with a different \\ base whose values can be computed . \\ x \log (3) & = \log (\frac{21}{1.7}) \\ x & = \frac{\log (\frac{21}{1.7})}{\log (3)} \\ x & = 2.288 \end{aligned}

::1.7_3x=213x211.7log(3x)=211.7log(211.7)...在此使用通用日志;自然日志也可以使用,以及任何其他可计算数值的基数不同的日志。xlog(3)=log(211.7)x=log(211.7)log(3)x=2.288

To rewrite $\begin{aligned} 1.7 \cdot 3^{x} = 21 \end{aligned}$ in the form $\begin{aligned} 3^{g (x)} = 21 \end{aligned}$ (without the factor 1.7), requires converting the factor 1.7 to 3 to some power, i.e., solving the problem $\begin{aligned} 1.7 = 3^{a} \end{aligned}$ .
::将表3g(x)=21(不包括系数1.7)中的1.73x=21改写为表3g(x)=21,要求将系数1.7至3转换为某种力量,即解决问题1.7=3a。

\begin{aligned} 3^{a} & = 1.7 \\ \log (3^{a}) & = \log (1.7) \\ a & = \frac{\log (1.7)}{\log (3)} \\ a & \approx 0.483 \end{aligned}

::3a=1.7log(3a)=log(1.7)a=log(1.7) log(3)a0.483

The original equation then becomes
::然后,最初的方程式变成

\begin{aligned} 1.7 \cdot 3^{x} & = 3^{a} \cdot 3^{x} \\ = 3^{(x + a)} \\ = 3^{(x + \frac{\log 1.7}{\log 3})} \\ \approx 3^{(x + 0.483)} \end{aligned}

::1. 7_ 3x= 3a_ 3x= 3( x+a)= 3( x+log=1.7 log_ 3) @ 3( x+0. 483)

and, $\begin{aligned} g (x) = x + \frac{\log 1.7}{\log 3} \approx x + 0.483 \end{aligned}$ .
::和, g(x) =x+log=1.7log=3x+0. 483。

Sometimes when solving equations that contain logarithms, an extraneous solution can result. This is a valid solution to a form of the original equation, that is not a solution for the original problem.
::有时当解答包含对数的方程式时,会得出一个不相干的解决办法。这是对原始方程式的一种有效的解决方案, 而不是对原始问题的解决方案。

Take the equation $\begin{aligned} \log_{2} (4 x) = 2 - \log_{2} (x) \end{aligned}$
::使用方程式对数 log2 ( 4x) =2 - log2 ( x)

To solve the equation, isolate the log function, and then perform an inverse operation to obtain $\begin{aligned} x \end{aligned}$ .
::要解析方程式, 分离日志函数, 然后进行反向操作以获取 x 。

\begin{aligned} \log_{2} (4 x) & = 2 - \log_{2} (x) \\ \log_{2} (4 x) + \log_{2} (x) & = 2 \\ \log_{2} (4 x^{2}) & = 2 \\ 4 x^{2} & = 2^{2} \\ x^{2} & = 1 \\ x & = 1, - 1 \end{aligned}

::log2( 4x) = 2 - log2( x) log2( 4x) + log2( (x) = 2log2( 4x2) = 24x2=22x2=1x=1- 1

Although, two results have been obtained, a check of the original problem shows that $\begin{aligned} x = - 1 \end{aligned}$ is not a solution because the log function is not defined for a negative argument. The only solution then is $\begin{aligned} x = 1 \end{aligned}$ . Always check for extraneous solutions to equations involving logarithms.
::虽然已经取得了两个结果,但对原始问题的检查表明, x% 1 不是一个解决方案, 因为日志函数不是为负参数定义的。唯一的解决方案是 x=1 。总是要检查对数等式的外部解决方案。

Examples
::实例

Example 1
::例1

Earlier, you were asked if $\begin{aligned} f (x) = 3^{x} \end{aligned}$ and $\begin{aligned} g (x) = \log x \end{aligned}$ are inverses.
::早些时候,有人问您 f( x) =3x 和 g( x) = logx 是反数。

If you indicated that $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are not inverses you were correct. For the two functions to be inverses $\begin{aligned} g [f (x)] = f [g (x)] = x \end{aligned}$ . Instead the following is true: $\begin{aligned} g [f (x)] = \log [3^{x}] = x \cdot \log 3 \end{aligned}$ . This illustrates the point that the two functions must have the same base. In this case, $\begin{aligned} f (x) \end{aligned}$ has a base of 3, and $\begin{aligned} g (x) \end{aligned}$ has a base of 10. The correct form of $\begin{aligned} g (x) \end{aligned}$ as the inverse would be $\begin{aligned} g (x) = \log_{3} x = \frac{\log x}{\log 3} \end{aligned}$ .
::如果您表示 f( x) 和 g( x) 不是反方向, 您是正确的。要将两个函数换成 verseg g[ f( x) =f[ g( x) =x。以下是真实的 : g[ f( x) =log* =log* [ 3x] =xlog* 3。这显示了两个函数必须具有相同基数的点。在这种情况下, f( x) 的基数为 3, g( x) 的基数为 10 。 g( x) 的正确形式为 g( x) =log3 =log_x=log* 3 。

Example 2
::例2

Find the inverse of the function $\begin{aligned} y = 3 \ln (x + 7) - 5 \end{aligned}$ .
::查找函数 y=3ln(x+7)- 5 的反方向。

To find the inverse function of $\begin{aligned} y = 3 \ln (x + 7) - 5 \end{aligned}$ (which is one-to-one), interchange the independent and dependent variables, and solve for $\begin{aligned} y \end{aligned}$ .
::查找y=3ln(x+7)-5(一对一)的反函数,交换独立和依附变量,并解决y。

\begin{aligned} 3 \ln (y + 7) - 5 & = x \\ \ln (y + 7) & = \frac{x + 5}{3} \\ y + 7 & = e^{\frac{x + 5}{3}} \\ y & = e^{\frac{x + 5}{3}} - 7 \end{aligned}

::3ln(y+7)-5=xln(y+7)=x+53y+7=ex+53y=ex+53y=ex+53-7

The inverse function $\begin{aligned} y = e^{\frac{x + 5}{3}} - 7 \end{aligned}$ is shown with $\begin{aligned} y = 3 \ln (x + 7) - 5 \end{aligned}$ in the figure below.
::倒数函数 y=ex+53-7 在下图中以y=3ln(x+7)-5显示。

Example 3
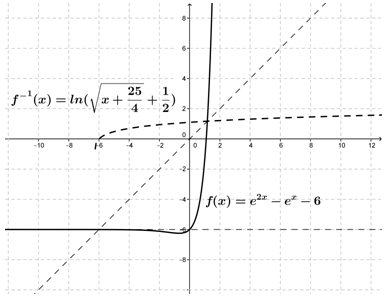
::例3

For the function $\begin{aligned} f (x) = e^{2 x} - e^{x} - 6 \end{aligned}$ , determine the roots of the function and the inverse of the function.
::对于函数 f(x) =e2x-ex-6, 确定函数的根和函数的反向。

$\begin{aligned} f (x) = e^{2 x} - e^{x} - 6 \end{aligned}$ can be written as $\begin{aligned} f (x) = (e^{x} + 2) (e^{x} - 3) \end{aligned}$ .
:x) =e2x- ex-6 可以写成 f(x) =(ex+2)(ex-3) 。

The only valid root, however, is $\begin{aligned} e^{x} = 3 \end{aligned}$ , because $\begin{aligned} e^{x} > 0 \end{aligned}$ .
::然而,唯一的有效根是 ex=3, 因为 ex>0 。

Therefore, $\begin{aligned} x = \ln 3 \approx 1.1 \end{aligned}$ .
::因此,x=ln=31.1。

To find the inverse, rewrite $\begin{aligned} f (x) \end{aligned}$ as $\begin{aligned} x = e^{2 y} - e^{y} - 6 \end{aligned}$ .
::要找到反义, 请将 f( x) 重写为 x=e2y-ey-6 。

Completing the square gives $\begin{aligned} x = {(e^{y} - \frac{1}{2})}^{2} - \frac{25}{4} \end{aligned}$ , or
::正在完成方块给定 x= (ey- 12) 2-254, 或

$\begin{aligned} e^{y} = \sqrt{x + \frac{25}{4}} + \frac{1}{2} \end{aligned}$ , or
::ey =x+254+12, 或

$\begin{aligned} y = \ln [\sqrt{x + \frac{25}{4}} + \frac{1}{2}] \end{aligned}$ , with $\begin{aligned} x \geq - \frac{25}{4} \end{aligned}$ .
::y=[x+254+12],加上x+254。

These results are shown in Figure below.
::这些结果见下图。

Review
::回顾

For all problems, solve for the variable $\begin{aligned} x \end{aligned}$ .
::对于所有问题,请解决变量 x 。

$\begin{aligned} 6^{x} = \frac{1}{216} \end{aligned}$
::6x=1216

$\begin{aligned} e^{x} = 3 \end{aligned}$
::ex=3 内ex=3

$\begin{aligned} \log_{2} x = 3 \end{aligned}$
::对数2x=3

$\begin{aligned} \ln (x^{2}) = 5 \end{aligned}$
::内( x2) = 5

$\begin{aligned} e^{- 5 x} = 132 \end{aligned}$
::e-5x=132

$\begin{aligned} e^{2 x} - 7 e^{x} + 10 = 0 \end{aligned}$
::e2x-7ex+10=0

$\begin{aligned} - 4 (3)^{x} = - 36 \end{aligned}$
::- 4(3)x36

$\begin{aligned} \ln x - \ln 3 = 2 \end{aligned}$
::内内 - 内 - 内 - 3=2

$\begin{aligned} y = 5 \log_{10} (\frac{2}{2 - x}) \end{aligned}$
::y= 5log10( 22- x)

$\begin{aligned} y = 3 e^{- \frac{2 x}{3}} \end{aligned}$
::y=3e- 2x3 y=3e- 2x3

$\begin{aligned} \log (x + 3) = \log (2 x) + \log 4 \end{aligned}$
:x+3)=log(2x)+log4

$\begin{aligned} \ln (4 x + 2) - \ln 6 = 7 \end{aligned}$
::内( 4x+2) - 内 6=7

$\begin{aligned} 5^{x + 1} = 6^{2 x} \end{aligned}$
::5x+1=62x

$\begin{aligned} \log_{5} (x - 2) + \log_{5} (6) = 3 \end{aligned}$
::对数 5(x-2)+log5(6)=3

$\begin{aligned} \log (2 x + 7) = \log 3 - \log (x + 1) \end{aligned}$
::log *% (2x+7) =log *3 -log* (x+1)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

指数函数和对数函数

Exponential and Logarithmic Functions ::指数函数和对数函数

The Exponential Function ::指数函数

Inverse of the Exponential Function: The Logarithmic Function ::指数函数的反对数函数:对数函数

Exponential and Logarithmic Function Relationship ::指数和对数函数关系

Solving problems involving Exponential and Logarithmic Functions ::涉及指数函数和对数函数的解决问题

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)