Course: 7.7 逆三角函数的衍生物

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

反逆三角函数的衍生物

If you are interested in baseball, you know that making contact with a fast ball is difficult, especially when the ball is thrown at speeds that can be up to 100 mph. What makes it difficult? The difficulty is the batter’s ability to follow the ball as it goes past the plate. The rate of change of the batter’s observing angle as the ball goes by is just too fast compared with the eye/brain’s ability to follow. The batter really does have to predict where the ball is going to be. Can you determine how fast a ball would have to be thrown so that a batter standing $\begin{align*}h\end{align*}$ feet from the plate would see the ball traveling with a rate of change of observing angle $\begin{align*}\frac{d\theta}{dt}\end{align*}$ no greater than 3 radians/sec (about the maximum rate the eye/brain can follow)?
::如果您对棒球感兴趣, 您知道与快速球接触是困难的, 特别是当球被以速度投出时, 速度可能高达100米。是什么使得它变得困难? 困难在于击手在球穿过球盘时能够跟踪球。球通过时击手的观测角度变化速度与眼睛/ 脑的跟踪能力相比太快。击手真的必须预测球会在哪里。您能否确定投球的速度有多快, 使球从球盘上站立起来的击手能够看到球在移动, 其观察角度的改变速度不超过3弧/ 秒( 眼睛/ 脑可以跟随的最大速度 ) ?

Derivatives of Inverse Trigonometric Functions
::反逆三角函数的衍生物

If $\begin{align*}u(x)\end{align*}$ is a differentiable function of $\begin{align*}x\end{align*}$ then the generalized derivative formulas for the inverse trigonometric functions are:
::如果 u(x) 是 x 可区分的函数,则反三角函数的通用衍生物公式是:

**of Inverse Trigonometric functions**
$\begin{align}\frac{d}{dx}[\arcsin u] = \frac{1}{\sqrt{1-u^2}}\frac{du}{dx}, \ \|u\|<1\end{align}$	$\begin{align}\frac{d}{dx}[\text{arc} \csc u] = \frac{-1}{\|u\|\sqrt{u^2-1}}\frac{du}{dx}, \ \|u\|>1\end{align}$
$\begin{align}\frac{d}{dx}[\arccos u] = \frac{-1}{\sqrt{1-u^2}}\frac{du}{dx}, \ \|u\|<1\end{align}$	$\begin{align}\frac{d}{dx}[\text{arc} \sec u] = \frac{1}{\|u\|\sqrt{u^2-1}}\frac{du}{dx}, \ \|u\|>1\end{align}$
$\begin{align}\frac{d}{dx}[\arctan u] = \frac{1}{1+u^2}\frac{du}{dx}\end{align}$	$\begin{align}\frac{d}{dx}[\text{arc} \cot u] = \frac{-1}{1+u^2}\frac{du}{dx}\end{align}$

Notice that there are just three results to remember because the other three are related by a change of sign:
::请注意,只有三个结果需要记住,因为其他三个结果因改变标志而相关:

$\begin{align*}\frac{d}{dx}[\arccos u]=-\frac{d}{dx}[\arcsin u]\end{align*}$
::ddx [arccos @ u] *ddx [arcsin_u] [arcsin_u] [arcsin_u] [addx] [arcsin_u] [arcsin_u]

$\begin{align*}\frac{d}{dx}[\text{arc} \cot u]=-\frac{d}{dx}[\arctan u]\end{align*}$
::ddx[arccotu] {ddx[arctanu] } dddx[arctanu]

$\begin{align*}\frac{d}{dx} [ \text{arc} \csc u ]= - \frac{d}{dx} [ \text{arc} \sec u ]\end{align*}$
::ddx [arccscu] [arcsecu]

The above relationships can each be derived using the following type of procedure example for $\begin{align*}\frac{d}{dx}[\arcsin u]\end{align*}$ , where we let $\begin{align*}y = \arcsin u\end{align*}$ :
::上述各种关系都可以使用以下类型的程序来推断,例如用于 ddx[arcsinu] 的 ddx[arcsinu] ,我们在此让 y=arcsinu :

\begin{aligned} y & = \arcsin u \\ \sin y & = \sin (\arcsin u) \\ \sin y & = u \\ \frac{d}{d x} [\sin y] & = \frac{d u}{d x} \\ \cos y \cdot \frac{d y}{d x} & = \frac{d u}{d x} \\ \frac{d y}{d x} & = \frac{1}{\cos y} \frac{d u}{d x} \\ \frac{d}{d x} [\arcsin u] & = \frac{1}{\sqrt{1 - \sin^{2} y}} \frac{d u}{d x} \\ \frac{d}{d x} [\arcsin u] & = \frac{1}{\sqrt{1 - u^{2}}} \frac{d u}{d x} \end{aligned}

$\begin{align*}y &= \arcsin u \\ \sin y &=\sin(\arcsin u) \\ \sin y &= u\\ \frac{d}{dx}[\sin y] &=\frac{du}{dx}\\ \cos y \cdot \frac{dy}{dx} &=\frac{du}{dx}\\ \frac{dy}{dx} &= \frac{1}{\cos y}\frac{du}{dx} \\ \frac{d}{dx}[\arcsin u] &= \frac{1}{\sqrt{1-\sin^2 y}}\frac{du}{dx}\\ \frac{d}{dx}[\arcsin u] &= \frac{1}{\sqrt{1-u^2 }}\frac{du}{dx}\end{align*}$
::yy=ddx[sin]=dudxcosydydx=1cosydudx[arcsinu]=11-sin2ydxdx[arcsinu]=11-sin2ydudxdx[arcsinu]=11-uddx

Now, use the formulas above to d ifferentiate $\begin{align*}y=\sin^{-1}\left(2x^4\right)\end{align*}$ .
::现在, 使用上面的公式来区分 y=sin- 1\\\\( 2x4) 。

Let $\begin{align*}u=2x^4\end{align*}$ . Then $\begin{align*}y=\sin^{-1}u\end{align*}$ .
::让你=2x4,然后你=1u。

Using the formula for $\begin{align*}\frac{d}{dx}[\sin^{-1}u]\end{align*}$ gives:
::使用 ddx [sin- 1_u] 提供的公式 :

\begin{aligned} \frac{d y}{d x} & = \frac{1}{\sqrt{1 - u^{2}}} \frac{d u}{d x} \\ = \frac{1}{\sqrt{1 - {(2 x^{4})}^{2}}} \cdot (8 x^{3}) \\ = \frac{8 x^{3}}{\sqrt{1 - 4 x^{8}}} \end{aligned}

$\begin{align*}\frac{dy}{dx} &=\frac{1}{\sqrt{1-u^2}}\frac{du}{dx}\\ &=\frac{1}{\sqrt{1-\left(2x^4\right)^2}}\cdot \left(8x^3\right)\\ &=\frac{8x^3}{\sqrt{1-4x^8}}\end{align*}$
:

dx)=11-u2dudx=11-(2x4)2(8x3)=8x31-4x8

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine how fast a ball would have to be thrown $\begin{align*}(\text{speed} = v)\end{align*}$ so that a batter standing $\begin{align*}h\end{align*}$ feet from the plate would see the ball traveling with a rate of change of observing angle $\begin{align*}\frac{d\theta}{dt}\end{align*}$ no greater than 3 radians/sec (about the maximum rate the eye/brain can follow).
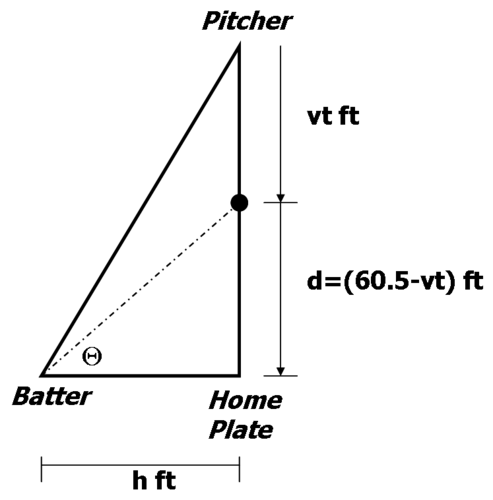
::早些时候,有人要求你确定投球的速度(速度=五),这样,一个站在板块上站着的击球手就会看到球在移动时,角的观察速度变化不大于3弧度/秒(眼睛/脑部可跟随的最大速度)。

A figure depicting the problem geometry is shown below.
::下面是描述问题几何的图。

The batter’s observing angle can be expressed as:
::殴打的观察角度可以表现为:

\begin{aligned} \tan θ (t) = \frac{d}{h} = \frac{60.5 - v t}{h} or θ (t) = arctan (\frac{60.5 - v t}{h}) \end{aligned}

$\begin{align*}\tan\theta (t) = \frac{d}{h}=\frac{60.5 - vt}{h} \text{ or } \theta(t) = \text{arctan} \left ( \frac{60.5-vt}{h}\right )\end{align*}$
::tan(t) =dh=60.5-vth 或 (t) = arctan(60.5-vth)

where 60.5 ft is the distance from the batter’s box to the pitcher, $\begin{align*}v\end{align*}$ is the velocity of the ball, and $\begin{align*}t\end{align*}$ is time in seconds.
::其中60.5英尺是打手盒子到投手的距离,v是球的速度,t是秒以内的时间。

The rate of change of $\begin{align*}\theta\end{align*}$ is $\begin{align*}\frac{d}{dt}\theta(t) = \frac{d}{dt}\text{arctan}\left(\frac{60.5-vt}{h}\right )=\frac{1}{1+\left(\frac{60.5-vt}{h}\right)^2}\left(\frac{-v}{h}\right)\end{align*}$ .
::的变速率为 ddt(t) =ddtarctan(60.5-vth) =11+(60.5-vth) 2(-vh)。

When the ball arrives at the plate, $\begin{align*}\frac{d}{dt}\theta(t)=\left(\frac{-v}{h}\right)\end{align*}$ , so that if $\begin{align*}h=3 \ ft\end{align*}$ and $\begin{align*}\frac{d}{dt}\theta(t)=3 \ radians/sec\end{align*}$ , then $\begin{align*}v=3 \cdot 3=9 \ ft/sec \approx 6 \ mph\end{align*}$ . This is 15-17 times slower than the 90 to 100 mph speeds thrown by good pitchers.
::当球到达板块时, ddt}(t) =(- vh),这样,如果h=3 ft, ddt}(t) =3 弧度/秒,那么 v=3}3}3 =9 ft/sec}6 mph。这比好投手投出的90至100mph的速度慢15-17倍。

Example 2
::例2

Differentiate $\begin{align*}\tan^{-1}\left(e^{3x}\right)\end{align*}$ .
::差异 tan- 1 ( e3x) 。

Let $\begin{align*}u=e^{3x}\end{align*}$ . Then $\begin{align*}y=\tan^{-1}u\end{align*}$ .
::琵иǐ 礛碞ǐ

Using the formula for $\begin{align*}\frac{d}{dx}[\tan^{-1}u]\end{align*}$ gives:
::使用 ddx [tan- 1_u] 给付的公式 :

\begin{aligned} \frac{d y}{d x} & = \frac{1}{1 + u^{2}} \frac{d u}{d x} \\ = \frac{1}{1 + {(e^{3 x})}^{2}} \cdot 3 e^{3 x} \\ = \frac{3 e^{3 x}}{1 + e^{6 x}} \end{aligned}

$\begin{align*}\frac{dy}{dx} &=\frac{1}{1+u^2}\frac{du}{dx}\\ &=\frac{1}{1+\left(e^{3x}\right)^2}\cdot 3e^{3x}\\ &=\frac{3e^{3x}}{1+e^{6x}}\end{align*}$
::uddx=11+u2dudx=11+(e3x)23e3x=3e3x1+e6x

Find $\begin{align*}\frac{dy}{dx}\end{align*}$ if $\begin{align*}y=\cos^{-1}(\sin x)\end{align*}$ .
::查找 dydx, 如果y=cos- 1 \\\\ (sinx) 的话。

Let $\begin{align*}u=\sin x\end{align*}$ . Then $\begin{align*}y=\cos^{-1}u\end{align*}$ .
::来来来来来来来来,然后你来来来来来来来

Using the formula for $\begin{align*}\frac{d}{dx}[\cos^{-1} u]\end{align*}$ gives:
::使用 ddx [cos- 1_u] 提供的公式 :

\begin{aligned} \frac{d y}{d x} & = \frac{- 1}{\sqrt{1 - u^{2}}} \frac{d u}{d x} \\ = \frac{- 1}{\sqrt{1 - \sin^{2} x}} \cos x \\ = - 1 \end{aligned}

$\begin{align*}\frac{dy}{dx} &=\frac{-1}{\sqrt{1-u^2}}\frac{du}{dx}\\ &=\frac{-1}{\sqrt{1-\sin^2 x}}\cos x\\ &=-1\end{align*}$
::11 -u2dudxx11 -sin2xcosx1

Example 3
::例3

Find the equation of the tangent line at $\begin{align*}(1,0)\end{align*}$ of the inverse function $\begin{align*}\arctan(x+y)=y^2+\frac{\pi}{4}\end{align*}$ .
::在arctan(x+y) =y24 的反函数(1,0)处查找正切线的方程。

First we need to find the slope $\begin{align*}y^{\prime}=\frac{dy}{dx}\end{align*}$ at (1,0). Then we write the equation of the line at that point.
::首先,我们需要在 1,0 点找到斜坡 yddx。然后我们写出线的方程。

\begin{aligned} \frac{d}{d x} [\arctan (x + y)] & = \frac{d}{d x} [y^{2} + \frac{π}{4}] \\ \frac{1}{1 + (x + y)^{2}} \frac{d}{d x} (x + y) & = 2 y y^{'} \\ \frac{1}{1 + (x + y)^{2}} (1 + y^{'}) & = 2 y y^{'} \\ y^{'} & = \frac{1}{1 - 2 y [1 + (x + y)^{2}]} \end{aligned}

$\begin{align*}\frac{d}{dx}[\arctan(x+y)] &= \frac{d}{dx}\left[y^2+\frac{\pi}{4}\right]\\ \frac{1}{1+(x+y)^2}\frac{d}{dx}(x+y)&=2yy^{\prime}\\ \frac{1}{1+(x+y)^2}(1+y^{\prime})&=2yy^{\prime}\\ y^{\prime}&=\frac{1}{1-2y[1+(x+y)^2]}\end{align*}$
::ddx[arctan}(x+y)]=ddx[y2][4]11+(x+y)2dx(x+y)=2yy_11+(x+y)2(1+y)2(1+y}=2y_y}11_2y[1+(x+y)2]

At (1,0), $\begin{align*}y^{\prime}=\frac{-1}{1-2\cdot 0[1+(1+0)^2]}=-1\end{align*}$ .
::1,0,y11-2,0[1+(1+0)2]

The tangent line has the form $\begin{align*}y=mx+b\end{align*}$ :
::相切线有y=mx+b的表单:

\begin{aligned} y & = m x + b \\ 0 & = - 1 \cdot 1 + b \\ b & = 1 \end{aligned}

$\begin{align*}y &= mx+b\\ 0 &=-1 \cdot 1+b\\ b &=1\end{align*}$
::y=mx+b0=1+bb=1 y=mx+b0=1+bb=1

The tangent line is $\begin{align*}y=-x+1\end{align*}$ .
::正切线是 yx+1 。

Review
::回顾

For #1-12, find the derivative with respect to the independent variable.
::对于 # 1- 12, 找到相对于独立变量的衍生物。

$\begin{align*}y=\sec^{-1}x^2\end{align*}$ .
::y=sec - 1\\\\\\x2 y=sec - 1\\\\\ x2.

$\begin{align*}y = \frac{1}{\tan^{-1}x}\end{align*}$ .
::y"1" -1"x。

$\begin{align*}y=\ln(\cos^{-1}x)\end{align*}$ .
::y= = = = (cos- 1x).

$\begin{align*}y = \sin^{-1}e^{-4x}\end{align*}$ .
::y'sin -1e -4x。

$\begin{align*}y=\sin^{-1}(x^2 \ln x)\end{align*}$ .
::y=sin-1(x2lnx)

$\begin{align*}y=3x^2 \arctan x\end{align*}$ .
::y=3x2arctanx。

$\begin{align*}y=\sin^{-1}\sqrt{2x}\end{align*}$ .
::y'sin -12x。

$\begin{align*}y=\tan^{-1}2t^3\end{align*}$ .
::y'tan -12t3。

$\begin{align*}x=\sin^{-1}\sqrt{1-t^4}\end{align*}$ .
::x=sin - 11 - t4 。

$\begin{align*}y=t\cot^{-1}(1+3t^2)\end{align*}$ .
::y=tcot-1(1+3t2)。

$\begin{align*}x=\frac{t}{\sqrt{1-t^2}}+\cos^{-1}t\end{align*}$ .
::x=t1 - t2+cos - 1_t.

$\begin{align*}z=\cot^{-1}\left(\frac{y}{1-y^2}\right )\end{align*}$ .
::z=cot-1(y1-y2)。

Find the relative extrema for $\begin{align*}y= \arcsin x-2 \arctan x\end{align*}$ .
::查找 y=arcsinx-2arctanx 的相对矩形。

What is the derivative of the function $\begin{align*}\cos(\arcsin x)\end{align*}$ .
::函数 cos( arcsinx) 的衍生物是什么。

Find the relative extrema for $\begin{align*}z=\frac{-e^{- \arcsin x}}{\sqrt{1-x^2}}\end{align*}$ .
::查找 z- arcsinx1- x2 的相对 extrema。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

$\begin{align}\frac{d}{dx}[\arcsin u] = \frac{1}{\sqrt{1-u^2}}\frac{du}{dx}, \ \|u\|<1\end{align}$	$\begin{align}\frac{d}{dx}[\text{arc} \csc u] = \frac{-1}{\|u\|\sqrt{u^2-1}}\frac{du}{dx}, \ \|u\|>1\end{align}$
$\begin{align}\frac{d}{dx}[\arccos u] = \frac{-1}{\sqrt{1-u^2}}\frac{du}{dx}, \ \|u\|<1\end{align}$	$\begin{align}\frac{d}{dx}[\text{arc} \sec u] = \frac{1}{\|u\|\sqrt{u^2-1}}\frac{du}{dx}, \ \|u\|>1\end{align}$
$\begin{align}\frac{d}{dx}[\arctan u] = \frac{1}{1+u^2}\frac{du}{dx}\end{align}$	$\begin{align}\frac{d}{dx}[\text{arc} \cot u] = \frac{-1}{1+u^2}\frac{du}{dx}\end{align}$

Section outline

General

反逆三角函数的衍生物

Derivatives of Inverse Trigonometric Functions ::反逆三角函数的衍生物

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)