Course: 7..11 反双曲函数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

反反双曲函数

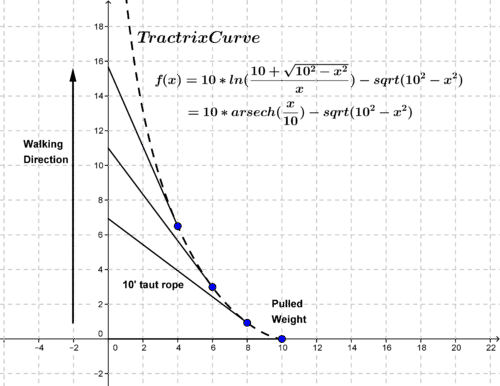
Suppose you are standing, facing north, and holding the end of a 10 foot, taut rope attached to a heavy weight that is positioned directly east of you. As you walk north steadily pulling the heavy weight (without jerking) along the ground’s, smooth, level surface, and keeping the rope taut, the path that the weight makes as it moves from its initial position is a curve that has a well known name in mathematics. This curve also describes the path taken by the middle of the rear wheel axle of a tractor trailer as it makes a turn perpendicular to its original direction of motion. Do you know the name of the curve? Do you have any idea how it relates to inverse hyperbolic functions ?
::假设你站着,朝北站着,拿着10英尺高的绳子,紧靠着紧靠东方的重重物。当你在北行时,沿着地面的平滑、平平的表面稳步拉动重物(不打手枪 ) , 并保持绳索的斜线, 重量从最初位置移动的路径是一条在数学上有着众所周知名字的曲线。此曲线还描述了拖拉机拖车后轮轴中间的路径, 因为它使转弯与最初运动方向垂直。您知道曲线的名称吗? 您知道它与反双曲函数有何关联吗 ?

Inverse Hyperbolic Functions
::反反双曲函数

The inverse hyperbolic functions are denoted as follows:
::反双曲函数如下:

**Hyperbolic function/inverse pairs**
$\begin{align}\sinh x \leftrightarrow \sinh^{-1} x \equiv ar \sinh x\end{align}$	$\begin{align}\text{csch} \ x \leftrightarrow \text{csch}^{-1} x \equiv ar \ \text{csch} \ x\end{align}$
$\begin{align}\cosh x \leftrightarrow \cosh^{-1} x \equiv ar \cosh x\end{align}$	$\begin{align}\text{sech} \ x \leftrightarrow \text{sech}^{-1} x \equiv ar \ \text{sech} \ x\end{align}$
$\begin{align}\tanh x \leftrightarrow \tanh^{-1} x \equiv ar \tanh x\end{align}$	$\begin{align}\text{coth} \ x \leftrightarrow \text{coth}^{-1} x \equiv ar \ \text{coth} \ x\end{align}$

The notation that uses “ar” as a prefix is an alternative way of indicating the inverse function.
::使用“ar”作为前缀的标记是表示反函数的另一种方式。

A function has an inverse if it is one-to-one. All of the hyperbolic functions except for $\begin{align*}\text{cosh} \ x\end{align*}$ are one-to-one functions and therefore have an inverse. Like the trigonometric functions, an inverse can be defined for $\begin{align*}\text{cosh} \ x\end{align*}$ by restricting its domain so that it is one-to-one. The table below provides a brief summary of characteristics of the six inverse hyperbolic functions.
::函数如果为一对一,则具有反向函数。除cosh x 外,所有双曲函数都是一对一函数,因此具有反向函数。与三角函数一样,可以通过限制 cos x 的域以一对一来对它进行反向定义。下表简要概述了六个反双曲函数的特性。

Inverse Function	Domain	Range	Basic Properties
$\begin{align}\sinh^{-1}x=\ln \left(x+\sqrt{x^2+1} \right)\end{align}$	$\begin{align}- \infty \le x \le \infty\end{align}$	$\begin{align}(- \infty, \infty)\end{align}$	$\begin{align}\sinh^{-1}(\sinh x)=\sinh(\sinh^{-1} x)=x\end{align}$
$\begin{align}\cosh^{-1}x=\ln \left(x+\sqrt{x^2-1} \right)\end{align}$	$\begin{align}x \ge 1\end{align}$	$\begin{align}[0, \infty)\end{align}$	$\begin{align}\cosh^{-1}(\cosh x)=\cosh(\cosh^{-1} x)=x\end{align}$
$\begin{align}\tanh^{-1}x=\frac{1}{2} \ln \frac{1+x}{1-x}\end{align}$	$\begin{align}\|x\| < 1\end{align}$	$\begin{align}(- \infty, \infty)\end{align}$	$\begin{align}\tanh^{-1}(\tanh x)=\tanh(\tanh^{-1}x)=x\end{align}$
$\begin{align}\text{csch}^{-1}(x) =\sinh^{-1} \left(\frac{1}{x} \right) \end{align}$ ::csch - 1 (x) =sinh - 1 (1x) $\begin{align}=\ln \left(\frac{1}{x} + \frac{\sqrt{1+x^2}}{\|x\|} \right)\end{align}$ ::=ln( 1x+1+x2}x)	$\begin{align}x \ne 0\end{align}$	$\begin{align}(- \infty, \infty)\end{align}$	$\begin{align}\text{csch}^{-1}(\text{csch}\ x)=\text{csch}(\text{csch}^{-1} x)=x\end{align}$
$\begin{align}\text{sech}^{-1}(x)=\cosh^{-1} \left(\frac{1}{x} \right)\end{align}$ ::sech- 1 (x) = cosh- 1 (1x) $\begin{align}=\ln \left(\frac{1+\sqrt{1-x^2}}{x} \right)\end{align}$ ::=ln( 1+1 - x2x)	$\begin{align}0 < x \le 1\end{align}$	$\begin{align}[0, \infty)\end{align}$	$\begin{align}\text{sech}^{-1}(\text{sech}\ x)=\text{sech}(\text{sech}^{-1} x)=x\end{align}$
$\begin{align}\text{coth}^{-1} x =\tanh^{-1} \left(\frac{1}{x} \right)\end{align}$ ::COth- 1x=tanh- 1( 1x) $\begin{align}=\frac{1}{2} \ln \frac{x+1}{x-1}\end{align}$ ::= 12lnx+1x-1	$\begin{align}\|x\| > 1\end{align}$	$\begin{align}y \ne 0\end{align}$	$\begin{align}\text{coth}^{-1}(\text{coth}\ x)=\text{coth}(\text{coth}^{-1} x)=x\end{align}$

The range is based on limiting the domain of the original function so that it is a one-to-one function.
::范围以限制原始函数域为基础,因此它是一个一对一的函数。

The hyperbolic function/inverse function pairs are graphed below:
::双曲函数/反向函数配对图如下:

If you are wondering how the explicit expressions for the inverse hyperbolic functions are derived, take a look at this problem.
::如果您想知道反双曲函数的明示表达式是如何产生的,请看一下这个问题。

Show that $\begin{align*}\sinh^{-1}x=ar \sinh x=\ln \left(x+\sqrt{x^2+1} \right)\end{align*}$ .
::显示 sinh- 1 @ x=arsinh@ x=ln @ (x+x2+1) 。

Let $\begin{align*}y=\sinh^{-1}x\end{align*}$ , then by definition
::依定义,让我们 y=sinh- 1\\\\ x

$\begin{align*}\sinh y=\frac{e^y-e^{-y}}{2}=\sinh(\sinh^{-1} \ x)=x\end{align*}$ .
:sinh-1x)=x。

Also, $\begin{align*}\cosh y=\frac{e^y+e^{-y}}{2}=\sqrt{1+\sinh^2 y}=\sqrt{1+x^2}\end{align*}$ , from the identity $\begin{align*}\cosh^2 y- \sinh^2 y=1\end{align*}$ .
::另外,Coshäy=ey+e-y2=1+sinh2@y=1+x2,来自身份cosh2@y-sinh2@y=1。

Consequently $\begin{align*}\sinh y+\cosh y=e^y=x+\sqrt{1+x^2}\end{align*}$ , which means
::因此,sinhy+coshy=ey=x+1+x2,这意味着

\begin{aligned} y = \ln (x + \sqrt{1 + x^{2}}) = \sinh^{- 1} x . \end{aligned}

$\begin{align*}y=\ln \left(x+\sqrt{1+x^2} \right)=\sinh^{-1}x.\end{align*}$
::y=ln(x+1+x2)=sinh-1x。

The other inverse hyperbolic functions can be derived in a similar manner.
::另一个反双曲函数也可以以类似的方式产生。

Here are some examples of how to evaluate the hyperbolic .
::以下是一些如何评估双曲的例子。

Evaluate each of the following:
::评估以下各项:

$\begin{align*}1. \tanh^{-1} \left(- \frac{7}{8} \right)\end{align*}$
::1.tanh-1(-78)

Given that $\begin{align*}\tanh^{-1} x=\frac{1}{2} \ln \frac{1+x}{1-x}\end{align*}$ , then
::鉴于 tanh - 1 x= 12ln1+x1 - x, 那么

\begin{aligned} \tanh^{- 1} (- \frac{7}{8}) & = \frac{1}{2} \ln | \frac{1 - \frac{7}{8}}{1 + \frac{7}{8}} | \\ = \frac{1}{2} \ln | \frac{\frac{1}{8}}{\frac{15}{8}} | \\ = \frac{1}{2} \ln \frac{1}{15} \\ \approx - 1.35 \end{aligned}

$\begin{align*}\tanh^{-1} \left(- \frac{7}{8} \right) &=\frac{1}{2} \ln \Bigg|\frac{1- \frac{7}{8}}{1+ \frac{7}{8}} \Bigg| \\ & =\frac{1}{2} \ln \Bigg|\frac{\frac{1}{8}}{\frac{15}{8}} \Bigg| \\ & =\frac{1}{2} \ln \frac{1}{15} \\ & \approx -1.35\end{align*}$
::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$\begin{align*}2. \sinh^{−1}3\end{align*}$
::2.sinh-1______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Given that $\begin{align*}\sinh^{-1} x=\ln \left(x+\sqrt{x^2+1} \right)\end{align*}$ , then
::鉴于 sinh- 1 x=ln ( x+x2+1) , 那么

\begin{aligned} \sinh^{- 1} 3 & = \ln (3 + \sqrt{3^{2} + 1}) \\ = \ln (3 + \sqrt{10}) \\ \approx 1.82 \end{aligned}

$\begin{align*}\sinh^{-1} 3 &=\ln \left(3+\sqrt{3^2+1} \right) \\ & =\ln \left(3+ \sqrt{10} \right) \\ & \approx 1.82\end{align*}$
::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\3+32+1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Examples
::实例

Example 1
::例1

Earlier, you were asked about walking north steadily pulling a heavy weight (without jerking) along the smooth surface and keeping the rope taught. The weight starts directly east of you and the path that the weight makes as it moves from its initial position is a curve that has a well known name in mathematics. Do you know the name of the curve? Do you have any idea how it relates to inverse hyperbolic functions?
::早些时候,有人问您如何沿着平滑的表面向北稳步走动,拉起沉重的重量(不打手枪),并保留绳索。重量直接从你身体的东部开始,而重量从最初位置移动时所走的路径是一条在数学中具有著名名称的曲线。您知道曲线的名称吗?您知道它与反双曲函数有什么关系吗?

The curve is called a tractrix , expressed by the function:
::曲线称为牵引线,以函数表示:

\begin{aligned} y = a \ln (\frac{a + \sqrt{a^{2} - x^{2}}}{x}) - \sqrt{a^{2} - x^{2}}, or y = a r {sech}^{- 1} (\frac{x}{a}) - \sqrt{a^{2} - x^{2}} \end{aligned}

$\begin{align*}y=a \ln \left(\frac{a+\sqrt{a^2-x^2}}{x} \right)- \sqrt{a^2-x^2}, \text{or} \ y=ar \text{sech}^{-1} \left(\frac{x}{a} \right) - \sqrt{a^2-x^2}\end{align*}$
::y=aln(a+a2-x2x)-a2-x2,或y=sarch-1(xa)-a2-x2

$\begin{align*}\text{sech} \ x\end{align*}$ .whose first term is the inverse of the function
::sech x. 其第一个任期是函数的反函数

Here is a curve of this example.
::这是这个例子的曲线。

Example 2
::例2

Find the equation of the inverse of the function $\begin{align*}y=\text{sech}(2x-3)+4\end{align*}$ and identify any restrictions.
::查找函数 y=sech( 2x-3) +4 的反方程式,并确定任何限制。

The function $\begin{align*}y=\text{sech}(2x-3)+4\end{align*}$ is not one-to-one. Using the restriction $\begin{align*}x \ge \frac{3}{2}\end{align*}$ makes the function one-to-one, and enables definition of an inverse.
::y=sech( 2x-3) +4 函数不是一对一。使用限制 x32 使函数一对一, 并允许对反定义。

The inverse is obtained by solving the equation $\begin{align*}x=\text{sech}(2y-3)+4\end{align*}$ for $\begin{align*}y\end{align*}$ , as follows:
::y的公式x=sech(2y-3)+4通过解析公式x=sech(2y-3)+4获得反差,具体如下:

\begin{aligned} sech (2 y - 3) + 4 & = x \\ sech (2 y - 3) & = x - 4 \\ (2 y - 3) & = {sech}^{- 1} (x - 4) \\ y & = \frac{1}{2} [{sech}^{- 1} (x - 4) + 3] \end{aligned}

$\begin{align*}\text{sech}(2y-3)+4 &=x \\ \text{sech}(2y-3) &=x-4 \\ (2y-3) &=\text{sech}^{-1}(x-4) \\ y &=\frac{1}{2} [\text{sech}^{-1}(x-4)+3]\end{align*}$
::sech( 2y-3)+4=xech( 2y-3)=x-4( 2y-3)=sech-1( X-4)y=12[ sech-1( x-4)+3]

Recall, however, that there is a restriction on the domain of the inverse $\begin{align*}\text{sech}^{-1} u\end{align*}$ : $\begin{align*}0 < u \le 1\end{align*}$ .
::然而,回顾指出,对反正sech-1u:0<u1的域有限制。

Therefore $\begin{align*}0 < x-4 \le 1\end{align*}$ , or $\begin{align*}4 < x \le 5\end{align*}$ .
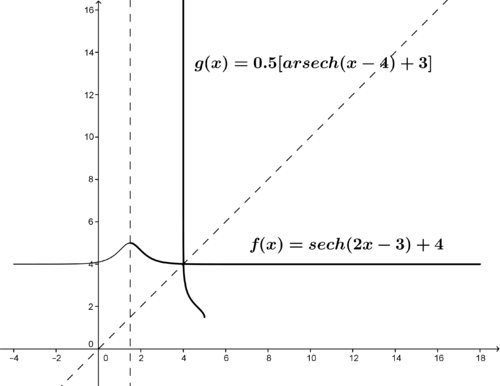
::因此, 0< x- 41, 或 4< x5。

The inverse of the function $\begin{align*}y=\text{sech}(2x-3)+4\end{align*}$ with $\begin{align*}x \ge \frac{3}{2}\end{align*}$ , is $\begin{align*}y=\frac{1}{2} [\text{sech}^{-1}(x-4)+3]\end{align*}$ with $\begin{align*}4 < x \le 5\end{align*}$ . The graph of function $\begin{align*}f(x)\end{align*}$ and the inverse $\begin{align*}g(x)\end{align*}$ are shown below.
::函数 y=sech(2x-3)+4加上 x32, y=12[sech-1(x-4)+3]加上 4<x=5。函数 f(x) 和反 g(x) 的图示如下。

Example 3
::例3

A tsunami wave was observed to have a speed $\begin{align*}v\end{align*}$ of $\begin{align*}XX\end{align*}$ and a wavelength $\begin{align*}\lambda\end{align*}$ of $\begin{align*}YY\end{align*}$ . Give an estimate of the depth of the body of the water $\begin{align*}d\end{align*}$ using the following equation for the speed:
::观察到海啸波的速率是XX,波长是YY。

$\begin{align*}v=\sqrt{\frac{g \lambda}{2 \pi} \tanh \left(2 \pi \frac{d}{\lambda} \right)}\end{align*}$ , where
::vg=223242424224222222222222222222222222222222222222222d22222222d222222222222224,vvg=g=222}}}}}}(2d222222224,其中

$\begin{align*}\lambda\end{align*}$ is the wavelength
::是波长

$\begin{align*}d\end{align*}$ is the depth, and
::d 是深度,并且

$\begin{align*}g\end{align*}$ is the acceleration of gravity.
::g 是重力加速度。

The speed is given by $\begin{align*}v=\sqrt{\frac{g \lambda}{2 \pi} \tanh \left(2 \pi \frac{d}{\lambda} \right)}\end{align*}$ .
::速度由 v=g2}( 2d) 给出。

Solving for the depth $\begin{align*}d\end{align*}$ gives
::深度 d 给予的解决方案

$\begin{align*}\tanh \left(2 \pi \frac{d}{\lambda} \right)=\frac{2 \pi v^2}{g \lambda}\end{align*}$ , so that
::tanh\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\d\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\d\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\v2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

$\begin{align*}d=\frac{\lambda}{2 \pi} \tanh^{-1} \left(\frac{2 \pi v^2}{g \lambda} \right)\end{align*}$ .
::2412222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222221222222222222222222222222222222222222

With $\begin{align*}\frac{2 \pi v^2}{g \lambda}=\frac{2 \pi \cdot v^2}{9.8 \cdot \lambda}\end{align*}$ , then
::加上2v2g2222v29.8,然后

$\begin{align*}\tanh^{-1}x=\frac{1}{2} \ln \frac{1+x}{1-x}\end{align*}$ , and
::tanh- 1x=12ln1+x1-x,以及

$\begin{align*}d=\frac{\lambda}{2 \pi} \tanh^{-1} \left(\frac{2 \pi v^2}{g \lambda} \right)\end{align*}$
::2122222

Review
::回顾

Show that $\begin{align*}\sinh \left(\ln \left[x+ \sqrt{1+x^2} \right] \right)=x\end{align*}$ .
::显示 sinh( ln[ x+1+x2]) =x 。

For #2-7, find the exact values of the inverse hyperbolic functions.
::# 2 7, 找到反双曲函数的准确值。

$\begin{align*}\sinh^{-1} 0\end{align*}$
::一九九至一九九九至一九九九至九九至九九至一一九九至九至九至九至九至九至九至九至一一一九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至一至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至九至一至一至一至十至十至十至十至九至九至九至九至九至九至九至九至九至九至九至九至九至一至九至九至九至九至九至九至九至九至九至九至九至九至一至九至九至九至九至九至九至一至一至一至九至九至九至九至九至九至九至九至九至九至九至十至九至九至九至九至九至九至九至九至九至九至九至

$\begin{align*}\cosh^{-1} 0\end{align*}$
::cosh- 1 @%0

$\begin{align*}\tanh^{-1} 0\end{align*}$
::tanh- 10

$\begin{align*}\sinh^{-1} 2\end{align*}$
::一九九至一一一二

$\begin{align*}\cosh^{-1} 1\end{align*}$
::cosh- 1 @% 1

$\begin{align*}\tanh^{-1} \frac{1}{2}\end{align*}$
::tanh-1112

For #8-12, find the exact value of $\begin{align*}x\end{align*}$ that satisfies the equation.
::对于#8-12, 找到满足方程式的x的准确值。

$\begin{align*}\text{coth}^{-1} x=\frac{1}{2}\end{align*}$
::COth- 1x= 12

$\begin{align*}\text{csch}^{-1} 3x=\frac{1}{2}\end{align*}$
::csch-13x=12

$\begin{align*}\text{cosh}^{-1} 4x=1\end{align*}$ .
::cosh- 14x= 1 。

$\begin{align*}2 \sinh x+ \cosh x=0\end{align*}$
::2sinhx+cooshx=0

$\begin{align*}3 \tanh x+ 5 \ \text{sech} \ x=5\end{align*}$
::3tanx+5 seech x=5 3tanx+5 seech x=5

For #13-15, find the equation of the inverse and identify any restrictions:
::对于第13-15号来说,找到反方方形,并找出任何限制:

$\begin{align*}y=2+\tanh \left(\frac{x+5}{3} \right)\end{align*}$
::y=2+tanh(x+53)

$\begin{align*}y=\sinh(x^2)\end{align*}$
::y=sinh(x2)

$\begin{align*}y=\sinh^2(x-4)-3\end{align*}$
::y=sinh2(x- 4)- 3

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

$\begin{align}\sinh x \leftrightarrow \sinh^{-1} x \equiv ar \sinh x\end{align}$	$\begin{align}\text{csch} \ x \leftrightarrow \text{csch}^{-1} x \equiv ar \ \text{csch} \ x\end{align}$
$\begin{align}\cosh x \leftrightarrow \cosh^{-1} x \equiv ar \cosh x\end{align}$	$\begin{align}\text{sech} \ x \leftrightarrow \text{sech}^{-1} x \equiv ar \ \text{sech} \ x\end{align}$
$\begin{align}\tanh x \leftrightarrow \tanh^{-1} x \equiv ar \tanh x\end{align}$	$\begin{align}\text{coth} \ x \leftrightarrow \text{coth}^{-1} x \equiv ar \ \text{coth} \ x\end{align}$

Inverse Function	Domain	Range	Basic Properties
$\begin{align}\sinh^{-1}x=\ln \left(x+\sqrt{x^2+1} \right)\end{align}$	$\begin{align}- \infty \le x \le \infty\end{align}$	$\begin{align}(- \infty, \infty)\end{align}$	$\begin{align}\sinh^{-1}(\sinh x)=\sinh(\sinh^{-1} x)=x\end{align}$
$\begin{align}\cosh^{-1}x=\ln \left(x+\sqrt{x^2-1} \right)\end{align}$	$\begin{align}x \ge 1\end{align}$	$\begin{align}[0, \infty)\end{align}$	$\begin{align}\cosh^{-1}(\cosh x)=\cosh(\cosh^{-1} x)=x\end{align}$
$\begin{align}\tanh^{-1}x=\frac{1}{2} \ln \frac{1+x}{1-x}\end{align}$	$\begin{align}\|x\| < 1\end{align}$	$\begin{align}(- \infty, \infty)\end{align}$	$\begin{align}\tanh^{-1}(\tanh x)=\tanh(\tanh^{-1}x)=x\end{align}$
$\begin{align}\text{csch}^{-1}(x) =\sinh^{-1} \left(\frac{1}{x} \right) \end{align}$ ::csch - 1 (x) =sinh - 1 (1x) $\begin{align}=\ln \left(\frac{1}{x} + \frac{\sqrt{1+x^2}}{\|x\|} \right)\end{align}$ ::=ln( 1x+1+x2}x)	$\begin{align}x \ne 0\end{align}$	$\begin{align}(- \infty, \infty)\end{align}$	$\begin{align}\text{csch}^{-1}(\text{csch}\ x)=\text{csch}(\text{csch}^{-1} x)=x\end{align}$
$\begin{align}\text{sech}^{-1}(x)=\cosh^{-1} \left(\frac{1}{x} \right)\end{align}$ ::sech- 1 (x) = cosh- 1 (1x) $\begin{align}=\ln \left(\frac{1+\sqrt{1-x^2}}{x} \right)\end{align}$ ::=ln( 1+1 - x2x)	$\begin{align}0 < x \le 1\end{align}$	$\begin{align}[0, \infty)\end{align}$	$\begin{align}\text{sech}^{-1}(\text{sech}\ x)=\text{sech}(\text{sech}^{-1} x)=x\end{align}$
$\begin{align}\text{coth}^{-1} x =\tanh^{-1} \left(\frac{1}{x} \right)\end{align}$ ::COth- 1x=tanh- 1( 1x) $\begin{align}=\frac{1}{2} \ln \frac{x+1}{x-1}\end{align}$ ::= 12lnx+1x-1	$\begin{align}\|x\| > 1\end{align}$	$\begin{align}y \ne 0\end{align}$	$\begin{align}\text{coth}^{-1}(\text{coth}\ x)=\text{coth}(\text{coth}^{-1} x)=x\end{align}$

Section outline

General

反反双曲函数

Inverse Hyperbolic Functions ::反反双曲函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)