10.4 查找二次曲线的参数等量:

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 查找二次曲线的参数等量:

  Collapse Expand

  查找二次曲线的参数等量:

  播放段落

  Bob plays outfield. He’s gotten to know the batters in his league pretty well, and has noticed that Mark always hits the ball at about the same speed and angle. Can Bob write an equation to figure out how long he has to get under a ball after Mark hits it?
  ::鲍勃在球场外打球。他非常了解球员队伍中的击球手,并且注意到马克总是以同样的速度和角度打球。 鲍勃能写一个方程式来弄清楚马克打球后他得在球下打多久?

  播放段落

  Parametric Equations of Parabolas
  ::Parabolas 参数等量

  播放段落

  In the past you've learned about in the form $\begin{align*}y=(x-h)^2-k\end{align*}$ , where  $\begin{align*}(h,k)\end{align*}$ is the vertex of the parabola . Parabolas describe many natural phenomena, including the motion of objects affected by gravity, the amounts of reagents during a chemical reaction, and how populations increase or decline in relation to one another. Sometimes, scientists need to know how two variables change with respect to time. To track how variables change over time, scientists can put equations into parametric form .
  ::过去,你以y=(x-h)2-k的形式了解到(h,k)是抛物线的顶点。Parabolas描述了许多自然现象,包括受重力影响的物体的动作、化学反应过程中的试剂数量,以及人口是如何增减的。有时,科学家需要知道两个变量在时间上是如何变化的。为了跟踪变量随时间变化的情况,科学家可以将等式设置为参数形式。

  播放段落

  Different can be used to represent a single parabola. For instance, two objects can travel the same parabolic path at two different speeds. 
  ::不同的参数可以用来代表单一的抛物线。例如,两个对象可以以两种不同的速度以相同的抛物线路径飞行。

  播放段落

  When you put an equation into parametric form, you rewrite  $\begin{align*}x\end{align*}$ and  $\begin{align*}y\end{align*}$ as functions of a third variable, usually  $\begin{align*}t\end{align*}$ for time. The resulting equation looks like this:
  ::当将方程式设置为参数形时,您将 x 和 y 重写为第三个变量的函数,通常时间为 t。结果的方程式看起来是这样的:

  播放段落

  $\begin{align*}F(t) = (x(t), y(t))\end{align*}$ , where  $\begin{align*}x(t)\end{align*}$ and  $\begin{align*}y(t)\end{align*}$ are both functions of a single variable, $\begin{align*}t\end{align*}$ .
  ::F(t) = (x(t) y(t) ), x(t) 和 y(t) 是单个变量 t 的函数 。

  播放段落

  For instance, the parabola  $\begin{align*}y=\frac{1}{4}x^2+3\end{align*}$ can be expressed by the following parametric equation :
  ::例如,抛物线y=14x2+3可以用下列参数方程表示:

  播放段落

  $$\begin{align*}F(t) &=(x(t), y(t))\\ x(t) &=2t\\ y(t) &=t^2+3\end{align*}$$
  ::F(t) = (x(t) y(t) ) x(t) = 2ty(t) = t2+3

  播放段落

  It can also be expressed by the parametric equation
  ::也可以用参数等式表示。

  播放段落

  $$\begin{align*}G(t) &=(x(t), y(t))\\ x(t) &=4t\\ y(t) &=4t^2+3\end{align*}$$
  ::G(t) = (x(t) y(t) ) x(t) = 4ty(t) = 4t2+3

  播放段落

  Let's sketch the parabola defined by the parametric equation
  ::让我们草草草草地画 由参数方程定义的抛物线

  播放段落

  $$\begin{align*}F(t) &=(x(t), y(t))\\ x(t) &=5t\\ y(t) &=20t+5t^2\end{align*}$$
  ::F(t) = (x(t) y(t) ) x(t) = 5ty(t) = 20t+5t2

  播放段落

  To sketch the parabola, you’ll need to put it in standard form. You can do this by eliminating $\begin{align*}t\end{align*}$  from the equation. Solve one equation for $\begin{align*}t\end{align*}$ , and substitute that value for $\begin{align*}t\end{align*}$  into the second equation.
  ::要绘制抛物线图, 您需要将其设置为标准格式。 您可以从等式中删除 t 。 解决 t 的一个方程式, 并将这个值替换为 t 。

  播放段落

  $$\begin{align*}x(t) &=5t\\ \frac{x}{5} &=t\\ y(t) &=20t+5t^2\\ y(t) &=20\left(\frac{x}{5}\right) +5\left(\frac{x}{5}\right)^2\\ y &=4x +\frac{5x^2}{25}\\ y &=\left(\frac{x^2}{5}\right)+4x\\ y &=\frac{1}{5} (x^2+20x)\end{align*}$$
  :t)=5tx5=ty(t)=20t+5t2y(t)=20(x5)+5(x5)+5(x5)2y=4x+5x225y=(x25)+4xy=15(x2+20x)

  播放段落

  Now, complete the square to put the equation into standard form.
  ::现在,完成方形,将方程式设置为标准形式。

  播放段落

  $$\begin{align*}y &= \frac{1}{5}(x^2+20x)\\ y &=\frac{1}{5}(x^2+20 x+100-100)\\ y &=\frac{1}{5}(x^2+20 x+100)-20\\ y+20 &=\frac{1}{5}(x+10)^2\end{align*}$$
  ::yy=15(x2+20x)y=15(x2+20x+100-100)y=15(x2+20x+100)y=15(x2+20x+100)-20y+20y=15(x+10)2

  播放段落

  The vertex for the parabola is at (-10, -20). Now, you can find the  $\begin{align*}x\end{align*}$ and  $\begin{align*}y\end{align*}$ intercepts to help you sketch it. To find the $\begin{align*}y\end{align*}$ -intercept, solve for  $\begin{align*}y\end{align*}$ when  $\begin{align*}x\end{align*}$ is 0.
  ::parbola 的顶点在 (- 10, - 20) 。 现在, 您可以找到 x 和 y 拦截来帮助您绘制它。 要找到 y 拦截, 在 x 0 时解决 y 。

  播放段落

  $$\begin{align*}y+20 &=\frac{1}{5}(x+10)^2\\ y+20 &=\frac{1}{5}(0+10)^2\\ y+20 &=\frac{1}{5} 100\\ y+20 &=20\\ y&=0\end{align*}$$
  ::y+20=15(x+1012y+20=15(0+102y)+20=15100y+20=20y=0

  播放段落

  The $\begin{align*}y\end{align*}$ -intercept for this parabola is at (0, 0). To find the $\begin{align*}x\end{align*}$ -intercepts, set  $\begin{align*}y\end{align*}$ to 0 and solve.
  ::此抛物线的 Y 界面为 0, 0 。 要找到 x 界面, 请将 y 设为 0 并解析 。

  播放段落

  $$\begin{align*}y+20 &=\frac{1}{5}(x+10)^2\\ 0+20 &=\frac{1}{5}(x+10)^2\\ 20&=\frac{1}{5}(x+10)^2\\ 100 &=(x+10)^2\\ \sqrt{100} &=\sqrt{(x+10)^2}\\ \pm 10 &= x+10\\ x&=0\\ x&=-20\end{align*}$$
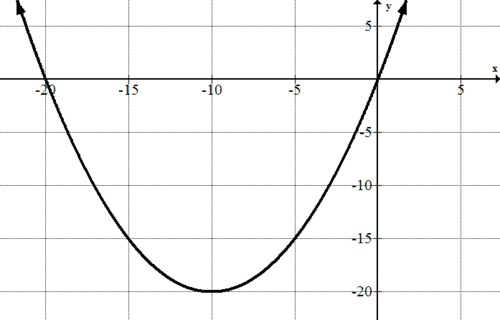
  ::y+20=15(x+10)20+20=15(x+10)220=15(x+10)220=15(x+10)2100=(x+10)21002((x+10)210=x+10=10x=0x#20

  播放段落

  So the $\begin{align*}x\end{align*}$ -intercepts for this parabola are at (0, 0) and (-20, 0). Use this information to sketch the graph.
  ::因此,这个抛物线的 X 界面在 0, 0 和 ( 20, 0) 上, 使用此信息绘制图形 。

  

  播放段落

  Often, a parametric equation will only describe a part of a parabola. You’ll need to determine what range of values satisfies the problem that you’re trying to solve. For example, an equation describing the motion of a projectile is only valid until it hits the ground. At that point, the projectile’s motion no longer follows a parabolic path.
  ::通常,参数方程式只能描述抛物线的一部分。 您需要确定什么值范围能满足您试图解决的问题。 比如,描述投射体运动的方程式只有在击中地面后才有效。 此时,投射体的运动不再遵循抛物线路径。

  播放段落

  Imagine a cliff diver takes a running leap off a 100 meter high cliff into the Mediterranean Sea. Until he breaks the surface of the water, his path can be described by the parametric equation:
  ::想象一下,悬崖潜水员从100米高的悬崖上跳跃到地中海。在他突破水面之前,他的路径可以用参数方程式来描述:

  播放段落

  $$\begin{align*}F(t) &=(x(t),y(t))\\ x(t) &=5.5t\\ y(t) &=-5 t^2 +100\end{align*}$$
  ::F(t) = (x(t),y(t)) ) x(t) = 5.5ty(t) 5t2+100

  播放段落

  For what values of  $\begin{align*}t\end{align*}$ is this parametric equation valid?
  ::这个参数方程的值是多少?

  播放段落

  Time starts at 0, and the equation ceases to be valid when he hits the water, which is when  $\begin{align*}y\end{align*}$ is 0. So, to find the values for $\begin{align*}t\end{align*}$ , substitute 0 for $\begin{align*}y(t)\end{align*}$ .
  ::时间从 0 开始, 当他击中水时, 方程式就不再有效, 也就是 y 是 0 。 所以, 要找到 t 的值, 替换 y (t) 的值, 替换 0 。

  播放段落

  $$\begin{align*}y(t) &=-5t^2 +100\\ 0 &=-5t^2 +100\\ -100 &=-5t^2\\ 20 &=t^2\\ \pm 2\sqrt{5} &=t\end{align*}$$
  ::y( t) 5t2+1000_5t2+100-100}5t220=t225=t

  播放段落

  A negative value for  $\begin{align*}t\end{align*}$ does not make sense within the context of this problem, so $\begin{align*}t = 2\sqrt{5}\end{align*}$ .
  ::t的负值在这一问题的背景下没有意义,所以t=25。

  播放段落

  At that point, the diver hits the water. This parametric equation is valid for values of  $\begin{align*}t\end{align*}$ on the interval from  $\begin{align*}t= 0\end{align*}$ to $\begin{align*}t=2\sqrt{5}\end{align*}$ .
  ::此时, 潜水员点击水面。 此参数方程对于 t=0 至 t=2 5 的间距 t 值有效 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked how Bob can model the trajectory of a baseball after Mark hits it. Bob can write a parametric equation to model the flight of the ball once it leaves Mark’s bat.
  ::早些时候,有人问到鲍勃如何在马克击球后模拟棒球的轨迹。 鲍勃在离开马克的球棒后可以写一个参数方程来模拟球的飞行。

  播放段落

  Assume that the batter’s bat is 1.3 meters off the ground when the ball hits it, that the ball travels at 10 m/s horizontally and 30 m/s vertically, and that the acceleration of gravity is $\begin{align*}10 \ m/s^2\end{align*}$ . If Bob is  $\begin{align*}5^\prime 10^{\prime\prime}\end{align*}$ tall, then he’ll catch the ball when it’s about 1.78 meters off the ground. The equation for the ball’s motion will be:
  ::假设击球击球时击球的球棒距离地面1.3米,球的高度为10米/秒,垂直为30米/秒/秒,重力加速度为10米/秒2,如果鲍勃高5英尺10英寸/秒,那么球离地约1.78米时他就会接球。球运动的方程式是:

  播放段落

  $$\begin{align*}F(t) &=(x(t),y(t))\\ x(t) &=10 t\\ y(t) &=30t + \frac{1}{2}(-10)t^2 +1.3\end{align*}$$
  ::F(t) = (x(t) y(t) ) x(t) = 10ty(t) = 30t+12(- 10) t2+1.3

  播放段落

  To find out when the ball will be 1.78 meters off the ground, set  $\begin{align*}y\end{align*}$ to 1.78 and solve for $\begin{align*}t\end{align*}$ .
  ::发现球何时会离地1.78米 设定到1.78米 解决 t

  播放段落

  $$\begin{align*}y(t) &= 30t + \frac{1}{2} (-10)t^2+1.3\\ 1.78 &=30t-5t^2+1.3\\ 0 &=-5t^2 +30t-.48\end{align*}$$
  ::y( t) = 30t+12(- 10) t2+1.31. 78= 30t- 5t2+1. 30@5t2+30- 30t- 48

  播放段落

  Use the quadratic formula to find the solutions:
  ::使用二次公式寻找解决方案 :

  播放段落

  $$\begin{align*}0 &= -5t^2 +30t-.48\\ t&=\frac{-30 \pm \sqrt{900+9.6}}{-10}\\ t&= \frac{-30\pm 30.16}{-10}\\ t &=6.016\end{align*}$$
  ::05t2+30t-.48t3090+9.6+10t}30_30_16_10t=6.016

  播放段落

  Only the positive solution to the equation matters, so Bob has about 6 seconds to move into position under Mark’s hit.
  ::所以鲍勃有大约6秒钟的时间在马克的打击下就位。

  播放段落

  Example 2
  ::例2

  播放段落

  A marine biologist discovers that the concentration of algae and the population of fish in a certain pond can be described by the parametric equation:
  ::海洋生物学家发现,藻类的浓度和某一池塘中的鱼类数量可以用参数等式来描述:

  播放段落

  $$\begin{align*}F(t) &=(x(t), y(t))\\ x(t) &= t^2 +10\\ y(t) &=3t\end{align*}$$
  ::F(t) = (x(t) y(t) ) x(t) = t2+10y(t) = 3t

  播放段落

  Put the equation into standard form, then graph it.
  ::将方程式放入标准格式,然后绘制图表。

  播放段落

  This equation describes a parabola with a horizontal, rather than a vertical, axis. Eliminate  $\begin{align*}t\end{align*}$ to put the equation in terms of  $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ .
  ::此方程式描述的是一个具有水平轴而非垂直轴的抛物线。 删除 t 以 x 和 y 表示方程式 。

  播放段落

  $$\begin{align*}y(t) &= 3t\\ \frac{y}{3} &=t\\ x(t) &=\left(\frac{y}{3}\right)^2 +10\\ x(t) &=\frac{1}{9}y^2 +10\\ x-10 &=\frac{1}{9}y^2\end{align*}$$
  ::y( t) = 3ty3= tx( t) = (y3) 2+10x( t) = 19y2+10x- 10=19y2

  播放段落

  The parabola has a vertex at (10, 0). You need only sketch the positive side of the parabola, since populations can’t be negative.
  ::抛物线在10,0时有一个顶点,你只需要勾画抛物线的正面,因为人口不可能是负的。

  播放段落

  Example 3
  ::例3

  播放段落

  Write the standard form for the parabola described by:
  ::写下下列抛物线的标准格式:

  播放段落

  $$\begin{align*}F(t) &= (x(t),y(t))\\ x(t) &= \frac{1}{2} t+3\\ y(t) &= 4t^2-1\end{align*}$$
  ::F( t) = (x( t) = (x( t) y( t) ) x( t) = 12t+3y( t) = 4t2- 1

  播放段落

  Eliminate the $\begin{align*}t\end{align*}$ to put the equation in terms of   $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ . Then complete the square to put the equation into standard form.
  ::消除 t 来将方程式以 x 和 y 表示。 然后完成方形, 将方程式以标准形式显示 。

  播放段落

  $$\begin{align*}x-3 &=\frac{1}{2}t\\ 2x-6 &=t\\ y(t) &=4t^2-1\\ y &=4(2x-6)^2-1\\ y &=4(4x^2 -24x+36)-1\\ y &=16x^2 -96x+144-1\\ y &=16x^2-96x+143\\ y &= 16(x^2 -6x+9)+143-144\\ y+1 &= 16(x-3)^2\end{align*}$$
  ::x-3=12t2x-6=ty(t)=4t2-1y=4(2x-6)2-1y=4(4x2-24x+36)2-1y=4(4x2-24x+36)-1y=16x2-96x+144-1y=16x2-96x-96x+143y=16(x2-6x+9)+143-144y+1=16(x-3)2

  播放段落

  The parabola has a vertical line of symmetry and a vertex at (3, -1).
  ::抛物线具有对称的垂直线和(3,-1)的顶点(3,-1)。

  播放段落

  Example 4
  ::例4

  播放段落

  A fabulous jumping frog takes a large leap. The parametric equation that describes its jump is
  ::跳起来的青蛙跳得惊人,跳得非常快。描述跳起来的参数方程式是:

  播放段落

  $$\begin{align*}F(t) &= (x(t), y(t))\\ x(t) &= .5t\\ y(t) &= 3t - 5t^2\end{align*}$$
  ::F(t) = (x(t) y(t) ) x(t) = 5ty(t) = 3t- 5t2

  播放段落

  How long is the frog in the air? How far does he jump?
  ::青蛙在空中多久,跳多远?

  播放段落

  First, find out how much time passes before the frog returns to the ground by solving for  $\begin{align*}t\end{align*}$ when  $\begin{align*}y\end{align*}$ is 0.
  ::首先,找出青蛙回到地上之前 有多少时间的经过 通过在 y 值 0 时解决 t 。

  播放段落

  $$\begin{align*}y(t) &=3t - 5t^2\\ 0 &=3t - 5t^2\end{align*}$$
  ::y( t) = 3t- 5t20= 3t- 5t2

  播放段落

  Use the quadratic formula to solve for $\begin{align*}t\end{align*}$ .
  ::使用二次公式解析 t。

  播放段落

  $$\begin{align*}t=\frac{-3\pm \sqrt{9+4(5)(0)}}{-10}\end{align*}$$
  ::===================================================================================================================================== =================================================================================================================================================================================================

  播放段落

  The fabulous frog was airborne for .6 seconds.
  ::神奇的青蛙在空中飞行了六秒半

  播放段落

  Now, substitute .6 into  $\begin{align*}x(t)\end{align*}$ to find the frog’s horizontal distance .
  ::现在, 将 6 替换为 x( t) 以找到青蛙的水平距离 。

  播放段落

  $$\begin{align*}x(t) &=.5t\\ x(t) &=.5(.6)\\ x(t) &=.3\end{align*}$$
  :t)=5tx(t)=5(6)x(t)=3

  播放段落

  The fabulous frog jumped a measly .3 meters.
  ::神奇的青蛙跳了0.3米

  播放段落

  Example 5
  ::例5

  播放段落

  Sketch the parabola defined by the following parametric equation.
  ::将以下参数方程界定的抛物线拉伸。

  播放段落

  $$\begin{align*}F(t) &= (x(t),y(t))\\ x(t) &= 5 t+3\\ y(t) &= 2t^2-5\end{align*}$$
  ::F( t) = (x( t) = (x( t) y( t) ) x( t) = 5t+3y( t) = 2t2- 5

  播放段落

  First, put the equation into standard form:
  ::首先,将方程式设置为标准形式:

  播放段落

  $$\begin{align*}x(t) &=5t+3\\ x-3 &=5t\\ \frac{1}{5}(x-3) &=t\\ y(t) &= 2t^2-5\\ y(t) &=2\left(\frac{1}{5}(x-3)\right)^2-5\\ y+5 &=\frac{2}{25}(x-3)^2\end{align*}$$
  ::x( t) = 5t+3x-3= 5t15( x-3) = ty( t) = 2t2- 5y( t) = 2( 15( x-3)) 2- 5y+5= 225( x-3) 2

  播放段落

  The vertex for the parabola is at (3, -5). Now find the  $\begin{align*}y\end{align*}$ and  $\begin{align*}x\end{align*}$ intercepts to help with the sketch.
  ::抛物线的顶点在( 3, 5) 。 现在找到 y 和 x 拦截的 y 和 x 来帮助绘制草图 。

  播放段落

  $$\begin{align*}y+5 &=\frac{2}{25}(x-3)^2\\ y+5 &=\frac{2}{25}(0-3)^2\\ y+5 &=\frac{18}{25}\\ y &=-4.28\\ (0,&-4.28) \end{align*}$$
  ::y+5=225(x-3)2y+5=225(0-3)2y+5=1825y4.28(0,-4.28)

  播放段落

  $$\begin{align*}y+5 &=\frac{2}{25}(x-3)^2\\ 0+5 &=\frac{2}{25}(x-3)^2\\ \frac{125}{2} &=(x-3)^2\\ \pm \frac{5\sqrt{10}}{2} &=x-3\\ (-4.91,0)&;(10.91,0) \end{align*}$$
  ::y+5=225(x-3)20+5=225(x-3)221252=(x-3)25102=x-3(-4.91,0);(10.91,0)

  播放段落

  Sketch the graph.
  ::绘制图表。

  播放段落

  Review
  ::回顾

  播放段落

  For #1-4, the parabola  $\begin{align*}y = \frac{1}{4}x^2+3\end{align*}$ can be expressed both of the following parametric equations:
  ::对于 # 1-4, 抛物线y=14x2+3可以表示以下两个参数方程:

  播放段落

  $$\begin{align*}F(t) &=(x(t), y(t))\\ x(t) &= 2t\\ y(t) &= t^2+3\end{align*}$$
  ::F(t) = (x(t) y(t) ) x(t) = 2ty(t) = t2+3

  播放段落

  AND
  ::和

  播放段落

  $$\begin{align*}G(t) &= (x(t), y(t))\\ x(t) &=4t\\ y(t) &= 4t^2 +3\end{align*}$$
  ::G(t) = (x(t) y(t) ) x(t) = 4ty(t) = 4t2+3

  播放段落
  1. Verify that both $\begin{align*}F(t)\end{align*}$  and $\begin{align*}G(t)\end{align*}$  model the parabola $\begin{align*}y = \frac{1}{4} x^2+3\end{align*}$ .
     ::验证 F(t) 和 G(t) 的参数 y= 14x2+3 模式。
  播放段落
  2. When would an object on $\begin{align*}F(t)\end{align*}$  reach (2, 4)? When would it reach (4, 7)?
     ::F(t)项上的物体何时达到(2,4)?该物体何时达到(4,7)?
  播放段落
  3. When would an object on $\begin{align*}G(t)\end{align*}$  reach (2, 4) When would it reach (4, 7)?
     ::G(t)上的物体何时达到(2,4)? 何时达到(4,7)?
  播放段落
  4. How much faster is an object moving along the parabola if it moves according to $\begin{align*}G(t)\end{align*}$  as opposed to $\begin{align*}F(t)\end{align*}$ ?
     ::如果一个物体按照G(t)而不是F(t)移动,在抛物线上移动的速度要快多少?

  播放段落

  For #5-7, write the standard form for each parabola:
  ::对于#5-7,写下每个抛物线的标准表格:

  播放段落
  5. $$\begin{align*}H(t) &=(x(t),y(t))\\ x(t) &= t+6\\ y(t) &=3t^2 -5\end{align*}$$
     ::H( t) = (x( t) = (x( t) y( t) ) x( t) = t+6y( t) = 3t2 - 5
  播放段落
  6. $$\begin{align*}J(t) &=(x(t), y(t))\\ x(t) &=\frac{1}{4}t-1\\ y(t) &= 3t^2\end{align*}$$
     ::J( t) = (x( t) = (x( t) y( t) ) x( t) = 14t- 1y( t) = 3t2
  播放段落
  7. $$\begin{align*}K(t) &=(x(t), y(t))\\ x(t) &= \frac{1}{4} t\\ y(t) &=t^2-1\end{align*}$$
     ::K(t) = (x(t) y(t) ) x(t) = 14ty(t) = t2- 1

  播放段落

  For #8-10, sketch the parabola defined by the given parametric equation:
  ::对于#8-10, 绘制给定的参数方程定义的抛物线草图:

  播放段落
  8. $$\begin{align*}L(t) &=(x(t), y(t))\\ x(t) &=2t+5\\ y(t) &=3t^2 -3\end{align*}$$
     ::L( t) = (x( t) = (x( t) y( t) ) x( t) = 2t+5y( t) = 3t2- 3
  播放段落
  9. $$\begin{align*}M(t) &=(x(t), y(t))\\ x(t) &=2t^2 -6\\ y(t) &=5t\end{align*}$$
     ::M(t)=(x(t),y(t))x(t)=2t2-6y(t)=5t
  播放段落
  10. $$\begin{align*}N(t) &=(x(t), y(t))\\ x(t) &=6t+1\\ y(t) &=t^2\end{align*}$$
      ::N(t) = (x(t) y(t) ) x(t) = 6t+1y(t) = t2

  播放段落

  For #11-13, a car drives off of a cliff that is 30 meters tall. Until it lands on the ground, its path can be described by the parametric equation:
  ::#11-13,一辆汽车从30米高的悬崖上驶下来,在降落在地面之前,其路径可以用参数方程来描述:

  播放段落

  $$\begin{align*}P(t) &=(x(t),y(t))\\ x(t) &=12t\\ y(t) &=\frac{1}{2}(-10)t^2+30\end{align*}$$
  ::P(t) = (x(t) y(t) ) x(t) = 12ty(t) = 12(-10) t2+30

  播放段落
  11. When will the car hit the ground? For what values of $\begin{align*}t\end{align*}$  is the parametric equation valid?
      ::汽车何时会撞到地面?
  播放段落
  12. Write the parametric equation in standard form and make a sketch of the situation.
      ::以标准形式写出参数方程 并对情况作一幅草图
  播放段落
  13. If the cliff is perpendicular to the ground, how far from the cliff will the car land?
      ::如果悬崖与地面垂直, 车离悬崖有多远?
  播放段落
  14. Find a parametric equation to model the parabola $\begin{align*}y=2x^2+5\end{align*}$ .
      ::找到一个参数方程来模拟抛物线y=2x2+5。
  播放段落
  15. Find another example of a parametric equation to model the parabola $\begin{align*}y= 2x^2+5\end{align*}$ .
      ::另找一个参数方程示例,以模拟抛物线y=2x2+5。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。