10.14 极表和微积分:曲线的长度

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 极表和微积分:曲线的长度

  Collapse Expand

  极表和微积分:曲线的长度

  播放段落

  Max’s sister’s wedding reception is underway, and the groomsmen are about to perform their awesome song and dance routine in honor of the couple’s love of acapella music. There’s just one problem. The groomsmen want to stay in range of the cardioid microphone that Max set up. Some of the more enthusiastic dancers keep stepping out of the microphone’s range. The wedding party wants a do-over, with tape on the floor to show them the boundaries of the cardioid. If Max wants to tape the perimeter of the area which feeds into the microphone, how much tape will he need? He’ll need to find the length of the cardioid's curve to find out.
  ::麦克斯姐姐的婚礼接待正在进行中,新郎们为了尊重这对夫妇对阿卡贝拉音乐的热爱,即将表演他们的精彩歌曲和舞蹈表演。只有一个问题。新郎们希望留在麦克斯设置的卡片麦克风范围内。一些更热心的舞者不断跳出麦克风的范围。婚礼派对想要一个跳台,在地板上放带带子,让他们看看卡片的界限。如果马克思想在麦克风中播映入的地区的周界贴上磁带,他需要多少磁带?他需要找到卡片曲线的长度才能找到答案。

  播放段落

  Finding the Length of a Curve in Polar Form
  ::在极形中查找曲线的长度

  播放段落

  To find the arc-length of a curve in polar form , you must find the length of the curve bounded by two angles. To find the arc length of a curve , you use the formula  $\begin{array}{r}l=\underset{a}{\overset{b}{\int }}\sqrt{r^2+{\left(\frac{dr}{d\theta }\right)}^2}d\theta \end{array}$ .
  ::要找到极形曲线的弧长度, 您必须找到以两个角度为界的曲线长度。 要找到曲线的弧长度, 您需要使用公式 labr2+( drd) 2d 。

  播放段落

  For some polar curves, the length formula produces integrals that you’ll be able to easily tackle with trigonometric or $\begin{array}{r}u\end{array}$  substitution. Other curves produce complicated integrals that demand numeric integration. Your integration method will depend on your situation.
  ::对于某些极曲线来说,长度公式产生整体体,您可以很容易地用三角或 u 替代处理。 其他曲线则产生复杂的整体体,需要数字整合。 您的整合方法将取决于您的情况。

  播放段落

  For instance, a sound technician would probably use a numeric integral in order to obtain concrete data on range, area, and potential feedback. Meanwhile a physicist might prefer to integrate symbolically so that she can use the same integral for multiple data sets. In this concept, you will focus on finding the lengths of curves that you can tackle without numeric integration.
  ::例如,音响技术员可能会使用数字集成来获取关于射程、面积和潜在反馈的具体数据。 与此同时,物理学家可能更愿意以象征性的方式整合,这样她就可以对多个数据集使用相同的集成。在这个概念中,你将侧重于找到无需数字集成就能解决的曲线长度。

  播放段落

  Let's find the arc length of  $\begin{array}{r}r=\sin \theta \end{array}$  from  $\begin{array}{r}\theta =0\end{array}$  to  $\begin{array}{r}\theta =\frac{\pi }{2}\end{array}$ .
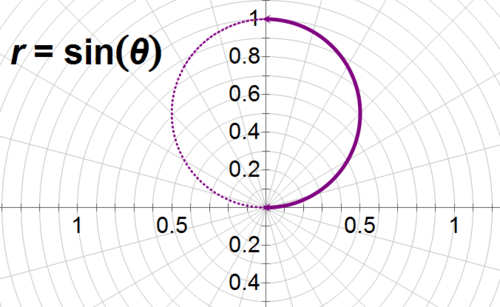
  ::让我们找到 r=sin 的弧长度, 从% 0 到% 2 。

  播放段落

  First, identify the shape and sketch the graph.  $\begin{array}{r}r=\sin \theta \end{array}$  is the equation for a circle in polar form. From  $\begin{array}{r}\theta =0\end{array}$   to  $\begin{array}{r}\theta =\frac{\pi }{2}\end{array}$  half of the circle (shown with the solid curve below).
  ::首先,指定形状并绘制图形的草图。 r=sin 是一个极形圆形的方程。 从 0 到 2 半圆形( 以下面的固体曲线显示) 。

  

  播放段落

  Now, use the arc length formula, and solve.
  ::现在,使用弧长度公式,然后解析。

  播放段落

  $$\begin{array}{rl}l& =\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{r^2+{\left(\frac{dr}{d\theta }\right)}^2}d\theta \\ & =\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{{\sin }^2\theta +{\cos }^2\theta }d\theta \\ & =\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{1}d\theta \\ & =[\theta {]}_0^{\frac{\pi }{2}}\\ & =\frac{\pi }{2}\end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}...

  播放段落

  Your circle had a radius of $\begin{array}{r}\frac{1}{2}\end{array}$ , and you found the arc length for a half circle. The geometric formula for the circumference of a circle is  $\begin{array}{r}C=\pi d\end{array}$ , where  $\begin{array}{r}d\end{array}$  is the diameter. This means that, according to geometry, the circumference of the half circle should be  $\begin{array}{r}\frac{1}{2}\pi (1)\end{array}$  or  $\begin{array}{r}\frac{\pi }{2}\end{array}$ . The formula for arc length in polar form yields the same measurement as the geometric formula.  
  ::您的圆的半径为 12, 您发现圆的弧长度为半圆。 圆环的几何公式是 Cd, d 是直径。 这意味着, 根据几何, 半圆的环圆应该是 12 (1) 或 2. 极形弧长度的公式产生与几何公式相同的测量值。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

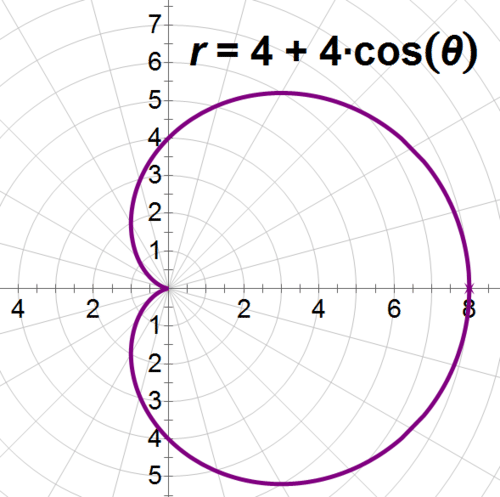
  播放段落

  Earlier, you were asked how  Max determine how much tape he needs to tape off the perimeter of the dance floor for the dancers. Max has found that the equation that describes the range of his cardioid microphone is $\begin{array}{r}r=4+4\cos \theta \end{array}$ , where $\begin{array}{r}r\end{array}$  is in feet. He can use this equation to figure out the perimeter of the region that he needs to tape around. If $\begin{array}{r}r=4+4\cos \theta \end{array}$ , then  $\begin{array}{r}l=\underset{0}{\overset{2\pi }{\int }}\sqrt{(4+4\cos \theta {)}^2+(-4\sin \theta {)}^2}d\theta \end{array}$   is the perimeter of the region.
  ::早些时候,有人问您Max如何确定他需要多少磁带才能从舞者舞池的周围磁带上绑下来。 Max发现描述其心型麦克风范围的方程式是 r=4+4cos, r是脚下的。 他可以用这个方程式来找出他需要绑在周围的周边区域。 如果 r=4+4cos, 那么, l02( 4+4cos)2+( - 4sin)2d是该地区的周边。

  

  播放段落

  Max is going to integrate from 0 to $\begin{array}{r}\pi \end{array}$  and double the length to find the whole measurement of the cardioid. He also takes advantage of the fact that  $\begin{array}{r}4+4\cos \theta =4(1+\cos \theta )\end{array}$ to rewrite the integral as
  ::最大值将从 0 到 整合, 并翻倍长度以找到对心类的完整测量。 他还利用 4+4cos%4 (1+cos%) 来将内装件重写为 4+4cos%4 (1+cos%) 。

  播放段落

  $$\begin{array}{r}l=2\underset{0}{\overset{\pi }{\int }}\sqrt{(4(1+\cos \theta ){)}^2+(-4\sin \theta {)}^2}d\theta \end{array}$$

  
  ::l=20(4( 1+cos))2+( - 4sin)2d

  播放段落

  Then, he simplifies.
  ::然后,他简化了。

  播放段落

  $$\begin{array}{rl}l& =2\underset{0}{\overset{\pi }{\int }}\sqrt{(4(1+\cos \theta ){)}^2+(-4\sin \theta {)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{16(1+2\cos \theta +{\cos }^2\theta )+16{\sin }^2\theta }d\theta \\ & =8\underset{0}{\overset{\pi }{\int }}\sqrt{1+2\cos \theta +{\cos }^2\theta +{\sin }^2\theta }d\theta \end{array}$$

  
  ::l=20(4( 1+cos) 2+( -4sin) 2016(1+2coscos2) +16sin2} 801+2coscos22sin2d

  播放段落

  He uses trigonometric substitution to get
  ::他用三角代法来代替

  播放段落

  $$\begin{array}{rl}& =8\underset{0}{\overset{\pi }{\int }}\sqrt{1+2\cos \theta +{\cos }^2\theta +{\sin }^2\theta }d\theta \\ & =8\underset{0}{\overset{\pi }{\int }}\sqrt{1+2\cos \theta +1}d\theta \\ & =8\underset{0}{\overset{\pi }{\int }}\sqrt{2+2\cos \theta }d\theta \end{array}$$

  
  ::=801+2cos22244801+2cos111802+2cosd222222422222422448001+2cos2444488801+2cos_1d8880}02+2cos2+2cosd4

  播放段落

  He multiplies by a form of one so that he has:
  ::以一种形式乘以倍增,所以他有:

  播放段落

  $$\begin{array}{rl}& =8\underset{0}{\overset{\pi }{\int }}\sqrt{2+2\cos \theta }d\theta \cdot \frac{\sqrt{2-2\cos \theta }}{\sqrt{2-2\cos \theta }}\\ & =8\underset{0}{\overset{\pi }{\int }}\frac{\sqrt{4-4{\cos }^2\theta }}{\sqrt{2-2\cos \theta }}d\theta \\ & =8\underset{0}{\overset{\pi }{\int }}\frac{\sqrt{4(1-{\cos }^2\theta )}}{\sqrt{2-2\cos \theta }}d\theta \end{array}$$

  
  ::=802+222222222804422222222242222222222222222222222222222222222222222222222222222222222

  播放段落

  Then he uses trigonometric substitution again to get: 
  ::然后他又用三角替代来获取:

  播放段落

  $$\begin{array}{rl}& =8\underset{0}{\overset{\pi }{\int }}\frac{\sqrt{4(1-{\cos }^2\theta )}}{\sqrt{2-2\cos \theta }}d\theta \\ & =8\underset{0}{\overset{\pi }{\int }}\frac{\sqrt{4({\sin }^2\theta )}}{\sqrt{2-2\cos \theta }}d\theta \\ & =8\underset{0}{\overset{\pi }{\int }}\frac{2\sin \theta }{\sqrt{2-2\cos \theta }}d\theta \end{array}$$

  
  ::=80422222222280422222222222222424222224224222422224224222222222442242222224424224222222222222224

  播放段落

  Max now has the problem in a form where he can use $\begin{array}{r}u\end{array}$  substitution to solve it.
  ::Max现在有麻烦了 他可以用U替代来解决

  播放段落

  $$\begin{array}{rl}& 8\underset{0}{\overset{\pi }{\int }}\frac{2\sin \theta }{\sqrt{2-2\cos \theta }}d\theta \\ & u=2-2\cos \theta \\ & du=2\sin \theta d\theta \\ & 8\int \frac{1}{\sqrt{u}}du\\ & =8\left[2u^{\frac{1}{2}}\right]=16{\left[\sqrt{2-2\cos \theta }\right]}_0^{\pi }=32\end{array}$$

  
  ::82222222222222281888888[222666222222222222222222222222222222

  播放段落

  He’ll need 32 feet of tape to mark out the floor space where the microphone works.
  ::他需要32英尺的磁带来标记麦克风工作的地面空间。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the arc length from 0 to $\begin{array}{r}2\pi \end{array}$  of $\begin{array}{r}r=1+\cos \theta \end{array}$ . 
  ::查找 r= 1+cos 0 到 2 的弧长度 。

  播放段落

  First, identify the curve and sketch a graph. This is the basic cardioid curve. Moving from 0 to $\begin{array}{r}2\pi \end{array}$  you have traced the entire curve one time.
  ::首先,指定曲线并绘制图表。 这是基本类固醇曲线。 从 0 移动到 2 , 您曾经跟踪过整个曲线 。

  

  播放段落

  The curve is symmetrical, so instead of finding the entire length, you can find half the length and then multiply it by 2.
  ::曲线是对称的,所以,与其找到整个长度,不如找到一半的长度,然后乘以2。

  播放段落

  Using the length formula, you’ll get:
  ::使用长度公式,你会得到:

  播放段落

  $$\begin{array}{rl}l& =\underset{a}{\overset{b}{\int }}\sqrt{r^2+{\left(\frac{dr}{d\theta }\right)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{(1+\cos \theta {)}^2+(-\sin \theta {)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{1+2\cos \theta +{\cos }^2\theta +{\sin }^2\theta }d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{1+2\cos \theta +1}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{2+2\cos \theta }d\theta \end{array}$$

  
  ::labr2+(drd)2d20(1+cos)2+(-sin)2d201+2coscos2}2{sin2}2d201+2cos}1d1d202+2cosd}

  播放段落

  Currently, the integral looks impossible – you have a quantity under a radical, with nothing that you can use as $\begin{array}{r}du\end{array}$  if you try to use $\begin{array}{r}u\end{array}$  substitution to integrate. Fortunately, there’s a simple trick to make this a bit easier to integrate. You can multiply the radical by a form of 1, and change its appearance.
  ::目前,整体体看起来不可能 — — 在激进下你有一个数量,而如果试图用u替代来整合,你什么也用不上。 幸运的是,有一个简单的把戏可以让它更容易整合。 你可以将激进化乘以1的形式,并改变其外观。

  播放段落

  $$\begin{array}{rl}& =2\underset{0}{\overset{\pi }{\int }}\sqrt{(2+2\cos \theta )}d\theta \cdot \frac{\sqrt{2-2\cos \theta }}{\sqrt{2-2\cos \theta }}\\ & =2\underset{0}{\overset{\pi }{\int }}\frac{\sqrt{4-4{\cos }^2\theta }}{\sqrt{2-2\cos \theta }}d\theta \end{array}$$

  
  ::=20(2+2cos)d22222222204 –4cos2222222222222222244222222242224222222222422222222422244422222224422224222222244

  播放段落

  Now, simplify and substitute. You’ll have put the integral into a form where you can use $\begin{array}{r}u\end{array}$  substitution.
  ::现在,简化和替代。你将把内装件放入一种可以使用 u 替代的形态。

  播放段落

  $$\begin{array}{rl}& =2\underset{0}{\overset{\pi }{\int }}\frac{\sqrt{4-4{\cos }^2\theta }}{\sqrt{2-2\cos \theta }}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\frac{2\sqrt{1-{\cos }^2\theta }}{\sqrt{2-2\cos \theta }}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\frac{2\sqrt{{\sin }^2\theta }}{\sqrt{2-2\cos \theta }}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\frac{2\sin \theta }{\sqrt{2-2\cos \theta }}d\theta \end{array}$$

  
  ::-====================================================================================================================================================== ======================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  Now, the numerator is the derivative of the quantity under the radical, so you can use $\begin{array}{r}u\end{array}$  substitution:
  ::现在,分子是基下数量的衍生物, 所以你可以使用 u 替代 :

  播放段落

  $$\begin{array}{rl}& 2\underset{0}{\overset{\pi }{\int }}\frac{2\sin \theta }{\sqrt{2-2\cos \theta }}d\theta \\ u& =2-2\cos \theta \\ du& =2\sin \theta d\theta \\ 2\int \frac{1}{\sqrt{u}}du& =2\int u^{-\frac{1}{2}}du=2\left[2u^{\frac{1}{2}}\right]\end{array}$$

  
  ::2222222222222212222222222222222222222222222222222222222222222222222222222222222222222222222222222222222

  播放段落

  Substitute the original terms for $\begin{array}{r}u\end{array}$ , and you get
  ::取代u的原条款,然后你得到

  播放段落

  $$\begin{array}{r}2{\left[2\sqrt{(2-2\cos \theta )}\right]}_0^{\pi }=4[2-0]=8\end{array}$$

  
  ::2[2(2)-2(cos)]0]4[2-0]=8

  播放段落

  Example 3
  ::例3

  播放段落

  Find the arc length of  $\begin{array}{r}r=\theta \end{array}$ from 0 to $\begin{array}{r}\pi \end{array}$ .
  ::查找 r 从 0 到 的弧长度 。

  播放段落

  First, identify the shape of the curve and sketch a graph. This is part of an Archimedean spiral, as shown below:
  ::首先,标明曲线的形状并绘制图表。这是Archimedean螺旋的一部分,如下所示:

  

  播放段落

  Now, use the length formula.
  ::现在,使用长度公式。

  播放段落

  $$\begin{array}{rl}l& =\underset{0}{\overset{\pi }{\int }}\sqrt{{\theta }^2+(1{)}^2}d\theta \\ & =\underset{0}{\overset{\pi }{\int }}\sqrt{{\theta }^2+1}d\theta \end{array}$$

  
  ::=================================================================================================================

  播放段落

  To simplify this integral, you’re going to have to use substitution. The range for the tangent function encompasses all real numbers. This means that for any value $\begin{array}{r}\theta \end{array}$ , there is some number $\begin{array}{r}x\end{array}$  where $\begin{array}{r}\theta =\tan x\end{array}$ . If $\begin{array}{r}\theta =\tan x\end{array}$ , then $\begin{array}{r}d\theta \end{array}$  will be equal to the derivative of $\begin{array}{r}\tan x\end{array}$ , so you get:
  ::要简化这个集成, 您必须使用替换。 相切函数包含所有真实数字的范围 。 这意味着对于任何值 {} {} , 有一些数字 x where tanx 。 如果 tanx, 那么 d 将等于 tanx 的衍生物, 所以您可以得到 :

  

  播放段落

  You’ll need to compute new limits of integration since you’re now integrating in terms of $\begin{array}{r}x\end{array}$  instead of in terms of $\begin{array}{r}\theta \end{array}$ . So:
  ::您需要计算新的整合限制, 因为您现在的整合是以 x 而不是 。 所以 :

  播放段落

  $$\begin{array}{rl}\theta & =0\\ \tan x& =0\\ x& ={\tan }^{-1}0=0\\ \theta & =\pi \\ \tan x& =\pi \\ x& ={\tan }^{-1}\pi \approx 1.262627\end{array}$$

  
  ::* 0tan*x=0x=tan -1*0=0*tan*x*x=tan -1*1*1.2627

  播放段落

  This means that your integral will look like this:
  ::这意味着你的内脏会变成这样:

  播放段落

  $$\begin{array}{r}\underset{0}{\overset{1.262627}{\int }}\sqrt{{\tan }^{2}x+1}{\sec }^{2}xdx\end{array}$$

  
  ::01.262627tan2x+1sec2xdx

  播放段落

  You can use trig identities to simplify.
  ::您可以使用 trig 身份来简化 。

  播放段落

  $$\begin{array}{rl}& =\underset{0}{\overset{1.262627}{\int }}\sqrt{{\tan }^{2}x+1}{\sec }^{2}xdx\\ & =\underset{0}{\overset{1.262627}{\int }}\sqrt{{\sec }^{2}x}{\sec }^{2}xdx\\ & =\underset{0}{\overset{1.262627}{\int }}{\sec }^{3}xdx\\ & =\frac{1}{2}{\left[\tan x\sec x-\ln \left(\cos \left(\frac{x}{2}\right)-\sin \left(\frac{x}{2}\right)\right)+\ln \left(\cos \left(\frac{x}{2}\right)+\sin \left(\frac{x}{2}\right)\right)\right]}_0^{1.262627}\end{array}$$

  
  ::01.262627tan2x+1sec2xxxxxxxxxxxxxxxxxxxxxxx2xse2xxxxxxxxx=12[tanxsecxxxxxxxxxxxxxxxxxxxxxxxxxxx2]+(x2)xxxxxxxxxxxxxxxxxxxxxx2xxx2xxxx2xxxxx2xxx2xxxx2xxxxxx2xxxx3xxxxxxxxxxxx=12[tanxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

  播放段落

  Now, find the solution. At 0, the quantity equals 0. At 1.262627, the quantity is: 6.1099. So the length of Archimedes’s spiral from 0 to $\begin{array}{r}\pi \end{array}$  is 6.1099 units.
  ::现在,找到解决办法。在0时,数量等于0。在1.262627, 数量是:6.1099。 所以Archimedes螺旋从0到____的长度是6.1099个单位。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the circumference of the circle $\begin{array}{r}r=6\cos \theta \end{array}$  in polar form.
  ::查找圆 r= 6cos 的极形环形。

  播放段落

  This is a circle with a radius of 3 units.
  ::这是一个半径为 3 个单位的圆形 。

  

  播放段落

  $$\begin{array}{rl}l& =\underset{a}{\overset{b}{\int }}\sqrt{r^2+{\left(\frac{dr}{d\theta }\right)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{(6\cos \theta {)}^2+(-6\sin \theta {)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{36{\cos }^2\theta +36{\sin }^2\theta }d\theta \\ & =12\underset{0}{\overset{\pi }{\int }}\sqrt{{\cos }^2\theta +{\sin }^2\theta }d\theta \\ & =12\underset{0}{\overset{\pi }{\int }}1d\theta \\ & =12[\theta {]}_0^{\pi }\\ & =12\pi \end{array}$$

  
  ::=======================================================================================================================================================

  播放段落

  Example 5
  ::例5

  播放段落

  Find the entire length of the cardioid $\begin{array}{r}r=8+8\sin \theta \end{array}$ . Sketch to find the boundaries of integration.
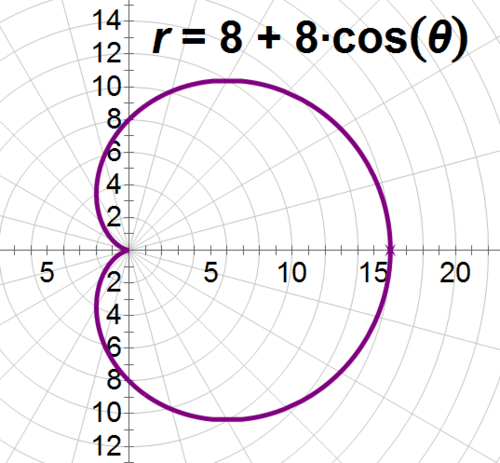
  ::查找整条心形机的长度=8+8sin。 要找到集成边界, 请用 Sletch 查找 。

  播放段落

  This is the basic cardioid curve. Moving from 0 to $\begin{array}{r}2\pi \end{array}$  you have traced the entire curve one time. Moving from 0 to $\begin{array}{r}\pi \end{array}$  you have traced the top half of the curve.
  ::这是基本类固醇曲线。 从 0 移动到 2 。 您曾经一次跟踪整个曲线。 从 0 到 移动, 您已经跟踪了曲线的上半部 。

  

  播放段落

  Integrate from 0 to $\begin{array}{r}\pi \end{array}$  and multiply the result by 2.
  ::将结果从 0 整合到 ,乘以 2。

  播放段落

  $$\begin{array}{rl}r& =8+8\sin \theta \\ l& =\underset{a}{\overset{b}{\int }}\sqrt{r^2+{\left(\frac{dr}{d\theta }\right)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{(8+8\sin \theta {)}^2+(8\cos \theta {)}^2}d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{64+128\sin \theta +64{\sin }^2\theta +64{\cos }^2\theta }d\theta \\ & =2\underset{0}{\overset{\pi }{\int }}\sqrt{64(1+2\sin \theta +{\sin }^2\theta +{\cos }^2\theta )}d\theta \\ & =16\underset{0}{\overset{\pi }{\int }}\sqrt{1+2\sin \theta +1}d\theta \\ & =16\underset{0}{\overset{\pi }{\int }}\sqrt{2+2\sin \theta }d\theta \end{array}$$

  
  ::r8+8sinlabr2+(drd)2d208+8sin)2+(8+8sin)2d2064+128sin64sin2}64cos222064(1+2sinsin22cos22)d}}16}01+2sin}1d}16}01+2sin}}1}16}02+2sind}}

  播放段落

  Multiply by a form of one and continue to integrate:
  ::乘以一种形式,并继续整合:

  播放段落

  $$\begin{array}{rl}& =16\underset{0}{\overset{\pi }{\int }}\sqrt{2+2\sin \theta }d\theta \cdot \frac{\sqrt{2-2\sin \theta }}{\sqrt{2-2\sin \theta }}\\ & =16\underset{0}{\overset{\pi }{\int }}\frac{2\sqrt{1-{\sin }^2\theta }}{\sqrt{2-2\sin \theta }}d\theta \\ & =16\underset{0}{\overset{\pi }{\int }}\frac{2\sqrt{{\cos }^2\theta }}{\sqrt{2-2\sin \theta }}d\theta \end{array}$$

  
  ::=16#0_2+2sin_2_2sin_2_2_2sin_1_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2__2_2_2_2________2__2___2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2_2___2_2_2_2_2_2__________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Split into two integrals because $\begin{array}{r}\cos \theta \end{array}$  is positive from 0 to $\begin{array}{r}\frac{\pi }{2}\end{array}$  but negative from $\begin{array}{r}\frac{\pi }{2}\end{array}$  to  $\begin{array}{r}\pi \end{array}$ .
  ::分解成两个构件, 因为 Cos 为正数 0 到 2, 但为负数 2 到 。

  播放段落

  $$\begin{array}{r}=16\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{2\cos \theta }{\sqrt{2-2\sin \theta }}d\theta +16\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}\frac{-2\cos \theta }{\sqrt{2-2\sin \theta }}d\theta \end{array}$$

  
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}=16... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}=16... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}=16...

  播放段落

  Use $\begin{array}{r}u\end{array}$  substitution and solve:
  ::使用 u 替换和解答:

  播放段落

  $$\begin{array}{rl}u& =2-2\sin \theta \\ du& =-2\cos \theta \\ & =-16\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{-2\cos \theta }{\sqrt{2-2\sin \theta }}d\theta +16\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}\frac{-2\cos \theta }{\sqrt{2-2\sin \theta }}d\theta \\ & =-16\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{\sqrt{u}}du+16\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}\frac{1}{\sqrt{u}}du\\ & =-16{\left[2u^{\frac{1}{2}}\right]}_0^{\frac{\pi }{2}}+16{\left[2u^{\frac{1}{2}}\right]}_{\frac{\pi }{2}}^{\pi }\\ & =-32{\left[\sqrt{(2-2\sin \theta )}\right]}_0^{\frac{\pi }{2}}+32{\left[\sqrt{(2-2\sin \theta )}\right]}_{\frac{\pi }{2}}^{\pi }\\ & =32\sqrt{2}+32\sqrt{2}\\ & =64\sqrt{2}\end{array}$$

  
  ::2222222222222222222222222222224161622266626626622222222322=642

  播放段落

  Review
  ::回顾

  播放段落
  1. Find the arc length of $\begin{array}{r}r=\theta \end{array}$  from $\begin{array}{r}\theta =0\end{array}$  to $\begin{array}{r}\theta =2\pi \end{array}$ .
     ::查找 r 的弧长度, 从 0 到 2 。
  播放段落
  2. Find the arc length of $\begin{array}{r}r=\cos \theta \end{array}$  from  $\begin{array}{r}\theta =0\end{array}$ to $\begin{array}{r}\theta =\frac{\pi }{2}\end{array}$ .
     ::查找 r=cos 的弧长度, 从% 0 到% 2 。
  播放段落
  3. Find the arc length from 0 to $\begin{array}{r}2\pi \end{array}$ of $\begin{array}{r}r=1+\sin \theta \end{array}$ .
     ::查找 r= 1+sin 0 到 2 的弧长度 。
  播放段落
  4. Find the circumference of $\begin{array}{r}r=4\sin \theta \end{array}$ .
     ::查找 r=4sin 的环度 。
  播放段落
  5. Find the length of $\begin{array}{r}r=2\theta \end{array}$  from 0 to $\begin{array}{r}\frac{\pi }{4}\end{array}$ .
     ::查找 r= 2 的长度, 从 0 到 4 。
  播放段落
  6. Find the entire length of the curve $\begin{array}{r}r=1-\cos \theta \end{array}$ .
     ::查找整个曲线的长度 r=1-cos。
  播放段落
  7. Find the length of the cardioid $\begin{array}{r}r=2+2\cos \theta \end{array}$ .
     ::查找心形 r=2+2cos的长度。
  播放段落
  8. Find the circumference of $\begin{array}{r}r=8\sin \theta \end{array}$ .
     ::查找 r= 8sin 的环绕值 。
  播放段落
  9. Find the arc length from 0 to $\begin{array}{r}\pi \end{array}$  of $\begin{array}{r}r=3+3\sin \theta \end{array}$ .
     ::查找 r= 3+3sin 0 到 的弧长度 。
  播放段落
  10. Find the arc length of $\begin{array}{r}r={\sin }^2\left(\frac{\theta }{2}\right)\end{array}$ .
      ::查找 r=sin2\\\\\\\\\\\\2 的弧长度 r=sin2\\\\\\\\\\\\\\ 。
  播放段落
  11. Find the circumference of $\begin{array}{r}r=2\cos \theta \end{array}$ .
      ::查找 r=2cos的环绕度 。
  播放段落
  12. Set up the integral to find the arc length of one petal of $\begin{array}{r}r=\cos 3\theta \end{array}$ . Don't evaluate.
      ::设置集成器以查找 r=cos3的花瓣的弧长度。 不要评价 。
  播放段落
  13. Set up the integral to find the arc length of one petal of $\begin{array}{r}r=\sin 4\theta \end{array}$ . Don't evaluate.
      ::设置集成件以查找 r=sin4的一瓣的弧长度。 不要评价 。
  播放段落
  14. Find the arc length of $\begin{array}{r}r={\cos }^3\left(\frac{\theta }{3}\right)\end{array}$  from  $\begin{array}{r}\theta =0\end{array}$  to $\begin{array}{r}\theta =\frac{3\pi }{2}\end{array}$ .
      ::查找 r=cos3 {{{{{{{{{{}} 的弧长度, 从0 到3} 2 的弧长度 。
  播放段落
  15. Find the arc length of $\begin{array}{r}r=\frac{\theta }{4}\end{array}$  from $\begin{array}{r}\theta =0\end{array}$  to $\begin{array}{r}\theta =2\pi \end{array}$ .
      ::查找 r4 的弧长度, 从 0 到 2 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。