Section outline

  • General

    Collapse all Expand all

  • 物理数学工具

    CSIRAC, Australia's first digital computer, showcasing its complex hardware and large structure.

    Scientists today use computers to aid with many complex mathematical operations used in science. Computers take and store measurement readings and can save hours, days, or even years of mathematical calculations. The image is of the CSIRAC (Council for Scientific and Industrial Research Automatic Computer), Australia's first digital computer, first run in November 1949. A modern laptop has more computing power than this room-filling computer did.
    ::今天,科学家们使用计算机来帮助许多复杂的数学操作用于科学。计算机接收并存储测量读数,可以节省数学计算的时间、天数甚至数年。图像是澳大利亚第一台数字计算机CSIRAC(科学和工业研究自动计算机理事会),该台数字计算机于1949年11月首次运行。 现代笔记本电脑的计算能力比这台填满房间的计算机要高。

    What Is the Place of Mathematics in Physics?
    ::数学在物理中的位置是什么?

    There is certainly a lot of math in physics , but the concepts and theories of physics cannot be derived from only mathematics. If you wish to build a complex mechanical structure, it is pointless to begin without wrenches and screwdrivers. To build mechanical structures, you must have tools. One of the primary tools for working in physics is mathematics. This particular physics resource requires algebra, geometry, and trigonometry, but higher-level physics courses also require calculus. In fact, calculus was invented by Isaac Newton specifically to solve physics problems; most advanced calculus problems are actually physics problems.
    ::物理学中当然有很多数学,但物理学的概念和理论不能只从数学中得出。如果你想建立一个复杂的机械结构,那么没有扳手和螺旋桨就毫无意义。要建立机械结构,你必须拥有工具。物理工作的主要工具之一是数学。这种特殊的物理资源需要代数、几何和三角测量,但高级物理课程也需要计算。事实上,牛顿(Isaac Newton)专门发明了微积分来解决物理问题;大多数先进的微积分问题实际上是物理问题。

    Scientific Notation
    ::科学符号

    In the "Definition of Physics," it was noted that physics deals with objects as small as sub-atomic particles and as large as galaxies. It should be clear that physicists deal with extremely small numbers - like the mass of a lead atom: 0.00000000000000000000034 g - and extremely large numbers - like the from our galaxy to the Andromeda galaxy: 2.5 million light years, which is approximately 25,000,000,000,000,000,000 km!
    ::在“物理定义”中,人们注意到物理学涉及小到亚原子粒子和星系的物体。应该清楚的是,物理学家涉及极小的数量,如铅原子的质量:00000000000000034克,以及极大的数量,如从银河系到安朵美达星系:250万光年,约为25,000,000,000,000公里!

    These numbers are difficult to write and even more difficult to calculate with. It is much more convenient to write and calculate with such extreme numbers if they are written in scientific notation . In scientific notation, the mass of a lead atom is 3.4 × 10 -22  g, and the distance from our galaxy to the Andromeda galaxy is 2.5 × 10 19 km.
    ::这些数字很难写,甚至更难以计算。如果以科学符号写出,用如此极端的数字来写和计算就更加方便。在科学符号中,铅原子的质量是3.4×10-22克,从银河系到安朵美达星系的距离是2.5×1019公里。

    A number is expressed in scientific notation by moving the decimal so that exactly one non-zero digit is on the left of the decimal and the exponent of 10 will be the number of places the decimal was moved. If the decimal is moved to the left, the exponent is positive and if the decimal was moved to the right, the exponent is negative. All significant figures are maintained in scientific notation. Significant figures are explained below.
    ::以科学符号表示一个数字,将小数点移到小数点,使小数点左边正好有一个非零位数,10的指数将是小数点移到小数点的位数。如果将小数点移到左边,则数字为正数,如果将小数点移到右边,则数字为负数。所有重要数字都保留在科学符号中。下文将解释重要数字。

    Example 1  
    ::例1

    Express 13,700,000,000 in scientific notation.
    ::科学注解中速达13 700 000 000美元。

    Since the decimal will be moved to the left 10 places, the exponent will be 10. So, the correct notation is 1.37 × 10 10 .
    ::由于小数点将移到左边的 10 位, 指数将是 10 。 因此, 正确的标记是 1. 37 × 1010 。

    Example 2  
    ::例2

    Express 0.000000000000000074 in scientific notation.
    ::在科学标记中,快递 100000000000074。

    Since the decimal will be moved to the right 17 places, the exponent will be -17. So the correct scientific notation is 7.4 × 10 -17 .
    ::由于小数点将移到正确的 17 位, 指数将是 - 17 。 因此正确的科学符号是 7. 4 × 10-17 。

    Example 3
    ::例3

    Express the number 8.43 × 10 5 in expanded form.
    ::8.43 x 105 号号以扩大格式表示。

    10 5 is 100,000 so 8.43 × 10 5 is 8.43 × 100,000 or 843,000.
    ::105等于100 000,8.43×105等于8.43×100 000或843 000。

    Operations with Exponential Numbers
    ::带有指数的操作

    In order to add or subtract numbers in scientific notation, the exponents must be the same. If the exponents are not the same, one of the numbers must be changed so that the exponents are the same. Once the exponents are the same, the numbers are added and the same exponents are carried through to the answer.
    ::为了在科学符号中添加或减去数字, 指数必须是相同的。 如果指数不相同, 就必须更改其中的一个数字, 以便指数是相同的。 一旦指数是相同的, 数字将被添加, 同样的指数会被传送到答案中 。

    Example 4  
    ::例4

    Add 5.0 × 10 5 and 4.0 × 10 4 .
    ::添加5.0×105和4.0×104。

    In order to add these numbers, we can change 4.0 × 10 4 to 0.40 × 10 5 and then add 0.40 × 10 5 to 5.0 × 10 5 which yields 5.4 × 10 5 .
    ::为了增加这些数字,我们可以将4.0×104改为0.40×105,然后增加0.40×105至5.0×105,产生5.4×105。

    When you multiply exponential numbers, the numbers multiply and the exponents add.
    ::当乘以指数数时,数字会乘以,引号会增加。

    Example 5  
    ::例5

    Multiply 5.0 × 10 5 and 4.0 × 10 4 .
    ::乘以 5.0 × 105 和 4.0 × 104.

      ( 5.0 × 10 5 ) ( 4.0 × 10 4 ) = ( 5.0 ) ( 4.0 ) × 10 5 + 4 = 20 × 10 9 = 2 × 10 10

    Example 6  
    ::例6

    Multiply 6.0 × 10 3 and 2.0 × 10 -5 .
    ::乘6.0×103和2.0×10-5。

    ( 6.0 × 10 3 ) ( 2.0 × 10 − 5 ) = 12 × 10 3 − 5 = 12 × 10 − 2 = 1.2 × 10 − 1 = 0.12

    When you divide exponential numbers, the numbers are divided and the exponent of the divisor is subtracted from the exponent of the dividend.
    ::当您将指数数除以指数数时,数字将被除以,从股息的指数中减去分数的指数。

    Example 7  
    ::例7

    Divide 6.0 × 10 3 by 2.0 × 10 -5 .
    ::6.0×103除以2.0×10-5。

      6.0 × 10 3 2.0 × 10 − 5 = 3.0 × 10 3 − ( − 5 ) = 3.0 × 10 8

    U se scientific notation to help you calculate each star's distance in the constellation Centaurus from our sun in the following PLIX Interactive:
    ::使用科学符号来帮助您计算星座中每颗恒星与太阳的距离, 在以下的 PLIX 互动中计算 :

     

     

    Significant Figures
    ::重要数字

    The numbers you use in math class are considered to be exact numbers. These numbers are defined, not measured. Measured numbers cannot be exact - the specificity with which we can make a measurement depends on how precise our measuring instrument is. In the case of measurements, we can only read our measuring instruments to a limited number of subdivisions. We are limited by our ability to see smaller and smaller subdivisions, and we are limited by our ability to construct smaller and smaller subdivisions on our measuring devices. Even with the use of powerful microscopes to construct and read our measuring devices, we eventually reach a limit. Therefore, although the actual measurement of an object may be a perfect 12 inches, we cannot prove it to be so. Measurements do not produce perfect numbers; the only perfect numbers in science are defined numbers, such as conversion factors .
    ::数学类中使用的数字被认为是精确的数字。 这些数字是定义的, 而不是测量的。 测量的数字是无法精确的。 测量的数字不能精确的—— 测量的特性取决于我们测量仪器的精确度。 在测量方面, 我们只能将测量仪器读到数量有限的分区。 我们看小小分区的能力有限, 测量设备上建造小小分区的能力也有限。 即使使用强大的显微镜来建造和阅读我们的测量设备, 我们最终还是达到了一个极限。 因此, 尽管一个物体的实际测量可能是一个完美的12英寸, 我们无法证明它是这样的。 测量并不产生完美的数字; 科学中唯一的完美数字是定义的数字, 如转换系数 。

    It is very important to recognize and report the limitations of a measurement along with the magnitude and unit of the measurement. Many times, the measurements made in an experiment are analyzed for regularities. Since the reported numbers show the limits of the measurements (how specific these measurements really are), it is possible to determine how regular these measurements are.
    ::承认和报告测量的局限性以及测量的规模和单位非常重要,在许多情况下,对实验中的测量进行了常规性分析,因为所报告的数字显示了测量的局限性(这些测量的实际具体程度),因此可以确定这些测量的经常性程度。

    Consider the Table of the pressures (P) and volumes (V) of a gas sample and the calculated PV product.
    ::考虑气体样本的压力表(P)和体积(V)以及计算出的光电池产品。

    Pressure Volume Pressure × Volume (P × V)
    4.01 atm 6.03 L 24.1803 L-atm
    3.02 atm 7.99 L 24.1298 L-atm
    6.04 atm 3.98 L 24.0392 L-atm
    11.98 atm 1.99 L 23.8402 L-atm

    Now, in the Table ,  look at this same set of data when we are told that all the measurements have only two significant figures and all the numbers must be rounded to two places.
    ::现在,在表格中,当我们被告知所有测量数据只有两个重要数字,所有数字必须四舍五入到两个位置时,请看这组数据。

    Pressure Volume Pressure × Volume (P × V)

    4.0 atm
    ::4时0分

    		6.0 L 24 L-atm
    3.0 atm 8.0 L 24 L-atm
    6.0 atm 4.0 L 24 L-atm
    12 atm 2.0 L 24 L-atm

    When the numbers are expressed with proper number of significant figures, a regularity appears that was not apparent before.
    ::当数字用适当数目的重要数字表示时,似乎以前没有明显的规律性。

    Rules for Determining Significant Figures
    ::确定重要数字的规则

    Significant figures are all of the digits that can be known with certainty in a measurement plus an estimated last digit. Significant figures provide a system to keep track of the limits of the original measurement. To record a measurement, you must write down all the digits actually measured, including measurements of zero, and you must not write down any digit not measured. The only real difficulty with this system is that zeros are sometimes used as measured digits, while other times they are used to locate the decimal point.
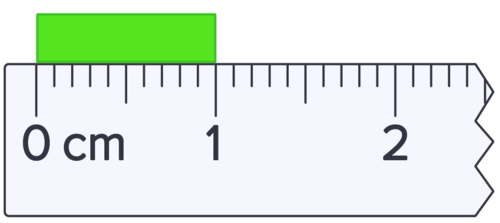
    ::重要数字都是在测量中可以肯定地知道的所有数字,加上估计的最后一位数字。 重要数字提供了一个跟踪原始测量极限的系统。 要记录测量, 您必须写下所有实际测量的数字, 包括零的测量, 并且您不能写下任何不测量的数字。 这个系统唯一的真正困难是, 零有时被作为测量数字使用, 而其它时候它们被用来定位小数点 。

    Ruler measuring a green object, calibrated to 0.1 centimeters.

    In the sketch shown above, the correct measurement is greater than 1.2 centimeters but less than 1.3 centimeters. It is proper to estimate one place beyond the calibrations of the measuring instrument. This ruler is calibrated to 0.1 centimeters, so we can estimate the hundredths place. This reading should be reported as 1.25 or 1.26 centimeters.
    ::在上文的草图中,正确的测量值大于1.2厘米,但小于1.3厘米。应该估计测量仪器校准以外的一个位置。这个标尺的校准值为0.1厘米,这样我们可以估计第一百个位置。这个读数应报告为1.25或1.26厘米。

     

    Ruler showing centimeters with a highlight indicating measurement for significant figures study.

    In this second case (sketch above), it is apparent that the object is, as nearly as we can read, 1 centimeter. Since we know the tenths place is zero and can estimate the hundredths place to be zero, the measurement should be reported as 1.00 centimeter. It is vital that you include the zeros in your reported measurement because these are measured places and are significant figures.
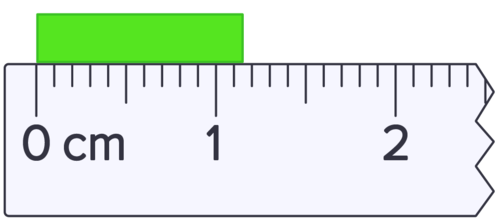
    ::在第二种情况(上文的伸展)中,很明显,该天体几乎是1厘米。由于我们知道十分位为零,并且可以估计第一百位为零,测量结果应报告为1.00厘米。你必须把零点列入你报告的测量中,因为这些是测量位置和重要数字。

     

    A ruler measuring an object, showing 1.15 or 1.16 centimeters.

    The measurement in the sketch above is read as 1.15 or 1.16 centimeters.
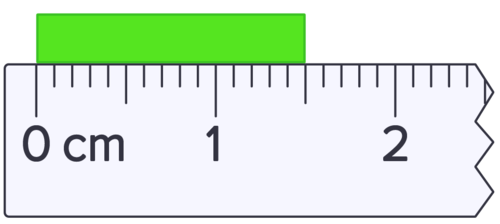
    ::上述草图中的测量值为1.15或1.16厘米。

     

    A ruler depicting measurements from 0 to 2 centimeters with a green object on it.

    The measurement in the sketch above is read as 1.50 centimeters.
    ::上述草图中的测量值为1.50厘米。

     

    In all of these examples, the measurements indicate that the measuring instrument had subdivisions of a tenth of a centimeter and that the hundredths place is estimated. There is some uncertainty about the last, and only the last, digit.
    ::在所有这些例子中,测量结果都表明测量仪器有十分之一厘米的细分,而且估计了第一百个位置。 对于最后一位、只有最后一位数字,还存在一些不确定性。

    In our system of writing measurements to show significant figures, we must distinguish between measured zeros and place-holding zeros. Here are the rules for determining the number of significant figures in a measurement.
    ::在我们的写作测量体系中,为了显示重要数字,我们必须区分测量的零和占位零。 这是确定测量中重要数字数量的规则。

    Rules for Determining the Number of Significant Figures
    ::确定重要数字数目的规则

    1. All non-zero digits are significant.
      ::所有非零位数都很重要。
    2. All zeros between non-zero digits are significant.
      ::非零位数之间所有零位数都很重要。
    3. All beginning zeros are not significant.
      ::所有起始零都不重要 。
    4. Ending zeros are significant if the decimal point is written in but not significant if the decimal point is an understood decimal (the decimal point is not written in).
      ::如果小数点是用小数点写入的,但如果小数点是理解的小数点(小数点不是用小数点写入的),则末数零是显著的。

    Examples of the Significant Figure Rules
    ::《重要图表规则》实例

    1. All non-zero digits are significant.
    ::1. 所有非零位数数字都很重要。

    543 has 3 significant figures.
    ::543有3个重要数字。

    22.437 has 5 significant figures.
    ::22 437有5个重要数字。

    1.321754 has 7 significant figures.
    ::1.321754有7个重要数字。

    2. All zeros between non-zero digits are significant.
    ::2. 非零位数之间所有零位数都很大。

    7,004 has 4 significant figures.
    ::7 004有4个重要数字。

    10.3002 has 6 significant figures.
    ::10.302有6个重要数字。

    103 has 3 significant figures.
    ::103有3个重要数字。

    3. All beginning zeros are not significant.
    ::3. 所有起始零数都不重要。

    0.00000075 has 2 significant figures.
    ::00000075有2个重要数字。

    0.02 has 1 significant figure.
    ::0.02有1个重要数字。

    0.003003 has 4 significant figures.
    ::0.003003有4个重要数字。

    4. Ending zeros are significant if the decimal point is actually written in but not significant if the decimal point is an understood decimal.
    ::4. 如果小数点是实际以小数点写入的,但如果小数点是理解的小数点,则小数点为零,则末数为零。

    37.300 has 5 significant figures.
    ::37.300有5个重要数字。

    33.00000 has 7 significant figures.
    ::33.00000有7个重要数字。

    100. has 3 significant figures.
    ::100. 有3个重要数字。

    100 has 1 significant figure.
    ::100有1个重要数字。

    302,000 has 3 significant figures.
    ::302 000有3个重要数字。

    1,050 has 3 significant figures.
    ::1 050有3个重要数字。

    Addition and Subtraction
    ::加和减

    The answer to an addition or subtraction operation must not have any digits further to the right than the shortest addend. In other words, the answer should have as many decimal places as the addend with the smallest number of decimal places.
    ::添加或减法操作的答案不得在右侧有任何位数。 换句话说, 答案应该与小数点后端的最小位数相同, 小数点后端的位数应该与小数点后端的位数相同。

    Example 8
    ::例8

    13.3843   cm   1.012   cm + 3.22   cm _     17.6163   cm = 17.62   cm

    ::13.3843厘米 1.012厘米+3.22厘米 - 17.6163厘米= 17.62厘米

    Notice that the top addend has a 3 in the last column on the right, but neither of the other two addends have a number in that column. In elementary math classes, you were taught that these blank spaces can be filled in with zeros and the answer would be 17.6163 cm. In the sciences, however, these blank spaces are unknown numbers, not zeros. Since they are unknown numbers, you cannot substitute any numbers into the blank spaces. As a result, you cannot know the sum of adding (or subtracting) any column of numbers that contain an unknown number. When you add the columns of numbers in the example above, you can only be certain of the sums for the columns with known numbers in each space in the column. In science, the process is to add the numbers in the normal mathematical process and then round off all columns that contain an unknown number (a blank space). Therefore, the correct answer for the example above is 17.62 cm and has only four significant figures.
    ::请注意, 顶端添加端在右侧的最后一列中有一个 3 , 但其他两个添加端都没有此列中的数字。 在基础数学类中, 您被告知这些空白空格可以填入零, 答案是17.6163厘米。 但是, 在科学方面, 这些空白空格是未知的数字, 不是零。 由于数字未知, 您无法将任何数字替换到空白空格中。 因此, 您无法知道添加( 或减去) 含有未知数字的任何列的总和。 在例中添加数字列时, 您只能确定列内每个空格中已知数字的列的总和。 在科学方面, 这一过程是在普通数学过程中添加数字, 然后将包含未知数字的所有列( 空白) 圆开。 因此, 以上示例的正确答案是17.62厘米, 并且只有四个重要数字 。

    Multiplication and Division
    ::计算和司

    The answer for a multiplication or division operation must have the same number of significant figures as the factor with the least number of significant figures.
    ::乘数或分部行动的答案必须具有与因数相同数量的重要数字,而因数最少。

    Example 9
    ::例9

    ( 3.556   cm ) ( 2.4   cm ) = 8.5344   cm 2 = 8.5   cm 2
    :sad3.556厘米)(2.4厘米)=8.5344厘米2=8.5厘米2

    The factor 3.556 cm has four significant figures, and the factor 2.4 cm has two significant figures. Therefore the answer must have two significant figures. The mathematical answer of 8.5344 cm 2 must be rounded back to 8.5 cm 2 in order for the answer to have two significant figures.
    ::3.556厘米的系数有四个重要数字,2.4厘米的系数有两个重要数字,因此答案必须有两个重要数字,8.5344厘米的数学答案必须四舍五入到8.5厘米,这样答案才能有两个重要数字。

    Example 10
    ::例10

    ( 20.0   cm ) ( 5.0000   cm ) = 100.00000   cm 2 = 100.   cm 2
    :sad20.0厘米)(5.0000厘米) = 1000000.00 厘米2 = 100.00 厘米2

    The factor 20.0 cm has three significant figures, and the factor 5.0000 cm has five significant figures. The answer must be rounded to three significant figures. Therefore, the decimal must be written in to show that the two ending zeros are significant. If the decimal is omitted (left as an understood decimal), the two zeros will not be significant and the answer will be wrong.
    ::20.0厘米的系数有三个重要数字,而5.00厘米的系数有五个重要数字。答案必须四舍五入到三个重要数字。因此,小数点必须写进去以显示两个结尾的零是显著的。如果省略了小数点(左为理解的小数点),则两个零点不会很大,答案也是错误的。

    Example 11
    ::例例11

    ( 5.444   cm ) ( 22   cm ) = 119.768   cm 2 = 120   cm 2
    :sad5 444厘米(22厘米)=119.768厘米2=120厘米2

    In this case, the answer must be rounded back to two significant figures. We cannot have a decimal after the zero in 120 cm 2 because that would indicate the zero is significant, whereas this answer must have exactly two significant figures.
    ::在这种情况下,答案必须四舍五入到两个重要数字。 我们不能在120厘米2的零之后再有一个小数点, 因为这意味着零是显著的, 而这个答案必须有两个重要数字。

    Further Reading
    ::继续阅读

    Summary
    ::摘要

    • Mathematics is a major tool for doing physics.
      ::数学是物理学的主要工具。
    • The very large and very small measurements in physics make it useful to express numbers in scientific notation.
      ::物理学中非常大和非常小的测量使得在科学符号中表达数字是有用的。
    • There is uncertainty in all measurements.
      ::所有测量都存在不确定性。
    • The use of significant figures is one way to keep track of uncertainty.
      ::使用重要数字是跟踪不确定性的一种方式。
    • Measurements must be written with the proper number of significant figures and the results of calculations must show the proper number of significant figures.
      ::计量必须用重要数字的适当数目来写,计算结果必须显示重要数字的适当数目。
    • Rules for Determining the Number of Significant Figures:
      • All non-zero digits are significant.
        ::所有非零位数都很重要。
      • All zeros between non-zero digits are significant.
        ::非零位数之间所有零位数都很重要。
      • All beginning zeros are not significant.
        ::所有起始零都不重要 。
      • Ending zeros are significant if the decimal point is actually written in but not significant if the decimal point is an understood decimal (the decimal point is not written in).
        ::如果小数点是实际以小数点写入的,但如果小数点是理解的小数点(小数点不是以小数点写入的),则末数零是显著的。

      ::确定重要数字数的规则:所有非零位数都很重要。非零位数之间的所有零都是重要的。所有起始数零都不重要。如果小数点实际以小数点表示,但如果小数点为理解的小数点(小数点未以小数点表示)不重要,则末数零是显著的。

    Review
    ::回顾

    1. Write the following numbers in proper scientific notation.
      1. 3,120
      2. 0.00000341

      ::在适当的科学符号中写下以下数字。 3,120 00000341。
    2. Write the following numbers in expanded form.
      1. 4.35 × 10 6
      2. 6.1 × 10 -4

      ::以扩展格式写下以下数字。 4. 35 × 106 6.1 × 10-4
    3. How many significant figures are in the following numbers?
      1. 2.3
      2. 17.95
      3. 9.89 × 10 3
      4. 170
      5. 1.02

      ::以下数字中有多少重要数字? 2.3 17.95 9.89 × 103 170 1.02
    4. Perform the following calculations and give your answer with the correct number of significant figures:
      1. 10.5 + 11.62
      2. 0.01223 + 1.01
      3. 19.85 − 0.0113

      ::进行下列计算,并用重要数字的正确数字回答: 10.5 + 11.62 0.0223 + 1.01 19.85 - 0.0113
    5. Perform the following calculations and give your answer with the correct number of significant figures:
      1. 0.1886 × 12
      2. 2.995 ÷ 0.16685
      3. 910 × 0.18945

      ::执行下列计算并给出正确数字的答案:0.1886 × 12 2.995 0.16685 910 × 0.18945

    Explore More
    ::探索更多

    Use the resource below to answer the questions that follow. 
    ::利用以下资源回答以下问题。

     

     

    1. How many base units are there?
      ::有多少基地单位?
    2. Why do we want the hours on top in the first conversion factor?
      ::为什么我们想要在第一个转换系数中 最上面的时数?
    3. What do measured numbers tell you?
      ::测量数字告诉你什么?
    4. What is the purpose of significant figures?
      ::重要数字的目的何在?