4.3 在角射入物体的投射声

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 弹射于角的物体的投射动作

  Collapse Expand

  弹射于角的物体的投射动作

  

  播放段落

  In the case of the human cannonball shown, all the vector and gravitational calculations must be worked out perfectly before the first practice session. With this activity, you cannot afford trial and error – the first miss might be the last trial.
  ::在显示的人类炮弹的情况下,所有矢量和引力计算都必须在第一次练习前完全完成。 通过这一活动,你无法承受试验和错误 — — 第一次失败可能是最后一次试验。

  播放段落

  Projectile Motion for an Object Launched at an Angle
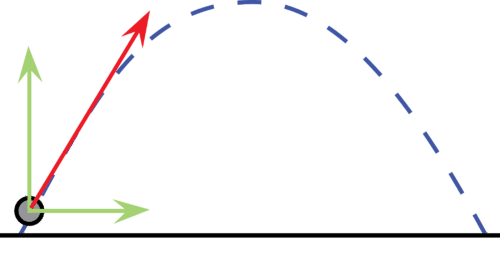
  ::弹射于角的物体的投射动作

  播放段落

  When an object is projected from rest at an upward angle, its initial can be resolved into two components. These two components operate independently of each other. The upward velocity undergoes constant downward which will result in it rising to a highest point and then falling backward to the ground. The horizontal motion is constant velocity motion and undergoes no changes due to gravity.The analysis of the motion involves dealing with the two motions independently. 
  ::当一个物体从向上角度从休息处投射时,其初始部分可分为两个组成部分。这两个组成部分相互独立运作。向上速度会持续向下,导致其升至最高点,然后向下向下向下。水平运动是恒定速度运动,不会因重力而发生任何变化。对运动的分析涉及独立处理两个动议。

  

  播放段落

  Example 1  
  ::例1

  播放段落

  A cannon ball is fired with an initial velocity of 100.0 m/s at an angle of 45° above the horizontal.  What maximum height will it reach and how far will it fly horizontally?
  ::大炮炮弹的最初速度为100.0m/s,发射角度为水平以上45°。它能达到的最高高度是多少,水平飞到多远?

  播放段落

  The first step in the analysis of this motion is to resolve the initial velocity into its vertical and horizontal components.
  ::分析这一动议的第一步是解决进入其纵向和横向组成部分的初始速度问题。

  播放段落

  $\begin{array}{r}{v}_{\text{i}-\text{up}}=(100.0\text{m/s})(\sin {45}^{\circ })=(100.0\text{m/s})(0.707)=70.7\text{m/s}\end{array}$
  ::vi-up=( 100.0 m/ s)( sin45) =( 100.0 m/ s ( 0. 707) = 70. 7 m/ s

  播放段落

  $\begin{array}{r}{v}_{\text{i}-\text{horizontal}}=(100.0\text{m/s})(\cos {45}^{\circ })=(100.0\text{m/s})(0.707)=70.7\text{m/s}\end{array}$
  :100.0m/s)(cos45)=(100.0m/s)(0.707=70.7m/s)

  播放段落

  We will deal with the vertical motion first. The vertical motion is symmetrical. As the object rises to its highest point and then falls back down, it will travel the same in each direction, and take the same amount of time. This is often hard to accept, but the amount of time the object takes to come to a stop at its highest point is the same amount of time it takes to return to where it was launched from. Similarly, the initial velocity upward will be the same magnitude (opposite in direction) as the final velocity when it returns to its original height. There are several ways we could approach the upward motion. We could calculate the time it would take gravity to bring the initial velocity to rest. Or, we could calculate the time it would take gravity to change the initial velocity from +70.7 m/s to -70.0 m/s.  Yet another way would be to calculate the time it takes for the object to return to its original height.
  ::我们将首先处理垂直运动。 垂直运动是对称的。 当物体升到最高点, 然后向下下降时, 它会向每个方向移动相同的方向, 并且花同样的时间。 这通常很难接受, 但物体在最高点停留的时间是返回发射地点所需的相同时间 。 同样, 初始速度向上是返回其原始高度时的最后速度( 方向对面 ) 。 我们可以用几种方法接近向上运动。 我们可以计算它需要重力的时间来使初始速度从+70.7 m/s /s 到 - 70.0 ms /s 。 或者, 我们可以计算它需要重力的时间来将初始速度从 +70.7 ms /s 改为 - 70.0 ms /s 。 另一种方式是计算物体返回原高度所需的时间 。

  播放段落

  $\begin{array}{r}{v}_f=v_i+at\text{so}t=\frac{v_f-v_i}{a}\end{array}$
  ::vf=vi+atsot=vf-via 组合键

  播放段落

  If we calculate the time required for the ball to rise up to its highest point and come to rest, the initial velocity is 70.7 m/s and the final velocity is 0 m/s. Since we have called the upward velocity positive, then the acceleration must be negative or -9.80 m/s ² .
  ::如果我们计算到球升到最高点并休息所需的时间, 最初的速度是70.7米/秒, 最终的速度是0米/秒。 既然我们称上方的速度为正, 那么加速度必须是负或- 9. 80米/秒。

  播放段落

  $\begin{array}{r}t=\frac{v_f-v_i}{a}=\frac{0\text{m/s}-70.7\text{m/s}}{-9.80{\text{m/s}}^2}=7.21\text{s}\end{array}$
  ::t=vf-via=0m/s-70.7m/s-9.80m/s2=7.21s

  播放段落

  Since this is the time required for the cannon ball to rise up to its highest point and come to rest, then the time required for the entire trip up and down would be double this value, or 14.42 s. The maximum height reached can be calculated by multiplying the time for the upward trip by the average vertical velocity. Since the object's velocity at the top is 0 m/s, the average upward velocity during the trip up is one-half the initial velocity.
  ::由于这是大炮球升至最高点并休息所需的时间,因此整个上下飞行所需的时间将是这一数值的两倍,即14.42秒。达到的最大高度可以通过将上上行时间乘以平均垂直速度来计算。由于天体顶部的速度是0米/秒,起上飞行的平均向上速度是最初速度的一半。

  播放段落

  $\begin{array}{r}{v}_{\text{up}-\text{ave}}=\left(\frac{1}{2}\right)(70.7\text{m/s})=35.3\text{m/s}\end{array}$
  :12) (70.7 m/s) = 35.3 m/s

  播放段落

  $\begin{array}{r}\text{height}=(v_{\text{up}-\text{ave}})(t_{\text{up}})=(35.3\text{m/s})(7.21\text{s})=255\text{m}\end{array}$
  ::高度=( vup- aave( tup) = (35.3 m/s)( 7.21 s) = 255 m

  播放段落

  The horizontal distance traveled during the flight is calculated by multiplying the total time by the constant horizontal velocity.
  ::飞行期间所穿行的水平距离是通过将总时间乘以常态水平速度计算的。

  播放段落

  $\begin{array}{r}{d}_{\text{horizontal}}=(14.42\text{s})(70.7\text{m/s})=1020\text{m}\end{array}$
  ::doritonal=(14.42秒)(70.7米/秒)=1020米

  播放段落

  Example 2  
  ::例2

  播放段落

  A golf ball was hit into the air with an initial velocity of 4.47 m/s at an angle of 66° above
  ::一枚高尔夫球被击入空中,最初速度为4.47米/秒,角度为66°以上

  播放段落

  the horizontal. How high did the ball go and how far did it fly horizontally?
  ::水平。球的高度是多高? 它水平飞到多远?

  播放段落

  $\begin{array}{r}{v}_{\text{i}-\text{up}}=(4.47\text{m/s})(\sin {66}^{\circ })=(4.47\text{m/s})(0.913)=4.08\text{m/s}\end{array}$
  :4.47 m/s)(sin66)=(4.47 m/s)(0.913)=4.08 m/s

  播放段落

  $\begin{array}{r}{v}_{\text{i}-\text{hor}}=(4.47\text{m/s})(\cos {66}^{\circ })=(4.47\text{m/s})(0.407)=1.82\text{m/s}\end{array}$
  :4.47 m/s)(cos66)=(4.47 m/s)(0.407=1.82 m/s)

  播放段落

  $\begin{array}{r}{t}_{\text{up}}=\frac{v_f-v_i}{a}=\frac{0\text{m/s}-4.08\text{m/s}}{-9.80{\text{m/s}}^2}=0.416\text{s}\end{array}$
  ::tup=vf-via=0m/s-4.08m/s-9.80m/s2=0.416s

  播放段落

  $\begin{array}{r}{v}_{\text{up}-\text{ave}}=\left(\frac{1}{2}\right)(4.08\text{m/s})=2.04\text{m/s}\end{array}$
  ::vup- ave=( 12) (4. 08 m/ s) = 2. 04 m/ s

  播放段落

  $\begin{array}{r}\text{height}=(v_{\text{up}-\text{ave}})(t_{\text{up}})=(2.04\text{m/s})(0.416\text{s})=0.849\text{m}\end{array}$
  ::高度=(vup-ave)(tup)=(2.04 m/s)(0.416 s)=0.849 m

  播放段落

  $\begin{array}{r}{t}_{\text{total trip}}=(2)(0.416\text{s})=0.832\text{s}\end{array}$
  ::总旅费=(2)(2)0.416s)=0.832s

  播放段落

  $\begin{array}{r}{d}_{\text{horizontal}}=(0.832\text{s})(1.82\text{m/s})=1.51\text{m}\end{array}$
  ::doritonal=(0.832秒)(1.82米/秒)=1.51米

  播放段落

  Example 3  
  ::例3

  播放段落

  Suppose a cannon ball is fired downward from a 50.0 m high cliff at an angle of 45° with an initial velocity of 80.0 m/s. How far horizontally will it land from the base of the cliff?
  ::假设炮弹从50米高的悬崖向下发射,角度为45度,最初速度为80.0米/秒。它从悬崖底部水平降落到多远?

  播放段落

  In this case, the initial vertical velocity is downward and the will increase this downward velocity.
  ::在这种情况下,最初的垂直速度是向下, 并会增加这种向下速度。

  播放段落

  $\begin{array}{r}{v}_{\text{i}-\text{down}}=(80.0\text{m/s})(\sin {45}^{\circ })=(80.0\text{m/s})(0.707)=56.6\text{m/s}\end{array}$
  ::vi- down= (80.0 m/s)(sin45) = (80.0 m/s)(0.707=56.6 m/s)

  播放段落

  $\begin{array}{r}{v}_{\text{i}-\text{hor}}=(80.0\text{m/s})(\cos {45}^{\circ })=(80.0\text{m/s})(0.707)=56.6\text{m/s}\end{array}$
  ::vi-hor= (80.0 m/s)(cos @45) = (80.0 m/s)(0.707=56.6 ms/s)

  播放段落

  $\begin{array}{r}d=v_{\text{i}-\text{down}}t+\frac{1}{2}a{t}^2\end{array}$
  ::d=六 - 下调+12at2

  播放段落

  $\begin{array}{r}50.0=56.6t+4.9t^2\end{array}$
  ::50.0=56.6t+4.9.9t2

  播放段落

  Changing to standard quadratic form yields  $\begin{array}{r}4.9t^2+56.6t-50.0=0\end{array}$
  ::改变为标准二次方形后,4.9t2+56.6t-5.0.0=0

  播放段落

  This equation can be solved with the quadratic formula. The quadratic formula will produce two possible solutions for $\begin{array}{r}t\end{array}$ :
  ::这个方程式可以用四方形公式来解决。四方形公式将为 t 产生两种可能的解决办法:

  播放段落

  $\begin{array}{r}t=\frac{-b+\sqrt{b^2-4ac}}{2a}\end{array}$ and $\begin{array}{r}t=\frac{-b-\sqrt{b^2-4ac}}{2a}\end{array}$
  ::tb+b2-4ac2a和tb-b2-4ac2a

  播放段落

  $\begin{array}{r}t=\frac{-56.6+\sqrt{(56.6{)}^2-(4)(4.9)(-50)}}{(2)(4.9)}=0.816\text{s}\end{array}$
  ::t56.6+(56.6)2-4(4)(4.9)(-50)(2)(4.9)=0.816 s

  播放段落

  The other solution to the quadratic formula is -12.375 s. Clearly, the cannon ball doesn't take -12 seconds to fly. Therefore, we take the positive answer. Using the quadratic formula will give you two answers; be careful to think about the answer you get - does it make sense?
  ::二次方程式的另一种解决办法是 - 12. 375 s. 显然, 大炮球不需要 - 12 秒才能飞翔。 因此, 我们采取肯定的答案。 使用二次方程式会给你们两个答案; 仔细考虑你得到的答案, 这是否有意义 ?

  播放段落

  To solve the problem, we plug the and time into the equation for distance:
  ::为了解决问题,我们把时间和时间插入到距离方程式中:

  播放段落

  $\begin{array}{r}{d}_{\text{horizontal}}=(0.816\text{s})(56.6\text{m/s})=46.2\text{m}\end{array}$
  ::doritonal=(0.816秒)(56.6米/秒)=46.2米

  播放段落

  In the following simulation, we can see that water from a fountain falls in a parabolic motion and lands at different positions based on its initial height, velocity and launch angle. Practice calculating where the water should land and then move the catcher to see if you are correct:
  ::在以下的模拟中,我们可以看到喷泉的水在抛物线运动中坠落,根据其最初的高度、速度和发射角度以不同的位置降落。

  播放段落

  Further Reading
  ::继续阅读

  播放段落

  Summary
  ::摘要

  播放段落
  • To calculate projectile motion at an angle, first resolve the initial velocity into its horizontal and vertical components.
    ::要从角度计算投影运动,首先将初始速度解析成其水平和垂直组件。
  播放段落
  • Analysis of projectile motion involves dealing with two motions independently.
    ::对射弹动议的分析涉及单独处理两项动议。
  播放段落
  • Vertical components will always have the acceleration of gravity acting on them.
    ::垂直组件将始终具有重力加速作用。
  播放段落
  • Vertical motion is symmetrical - the distance and time are the same in the rise as in the fall; the final velocity will have the same magnitude as the initial velocity but in the opposite direction.
    ::垂直运动是对称的 - 升起时的距离和时间与跌倒时的距离和时间相同; 最终速度与初始速度的高度相同,但方向相反。
  播放段落
  • Horizontal components will never be effected by gravity; it is constant velocity motion.
    ::水平组件永远不会受重力影响;它是恒定速度运动。

  播放段落

  Review
  ::回顾

  播放段落
  1. A player kicks a football from ground level with a velocity of magnitude 27.0 m/s at an angle of 30.0° above the horizontal.
     播放段落
     1. Find the time the ball is in the air.
        ::找到球在空中的时间
     播放段落
     2. Find the maximum height of the ball.
        ::找到球的最大高度。
     播放段落
     3. Find the horizontal distance the ball travels.
        ::找到球穿梭的水平距离
     
     ::玩家从地面踢足球,速度为27.0米/秒,角度在水平上方30.0°。找到球在空中的时间。找到球的最大高度。找到球的横向距离。
  播放段落
  2. A person standing on top of a 30.0 m high building throws a ball with an initial velocity of 20. m/s at an angle of 20.0° below horizontal. How far from the base of the building will the ball land?
     ::一个人站在30.0米高楼顶上,将最初速度为20米/秒的球投在水平下20.0度角下方。球落地离大楼底部多远?
  播放段落
  3. An arrow is fired downward at an angle of 45 degrees from the top of a 200 m cliff with a velocity of 60.0 m/s.
     播放段落
     1. How long will it take the arrow to hit the ground?
        ::箭要多久才能落地?
     播放段落
     2. How far from the base of the cliff will the arrow land?
        ::箭头离悬崖底部有多远?
     
     ::箭头从200米悬崖顶部向下射向45度角,速度为60.0米/秒。箭头要射向地面多久?箭头离悬崖底部有多远?

  播放段落

  Explore More
  ::探索更多

  播放段落

  Use this video to answer the questions that follow.  
  ::使用这段视频回答接下来的问题。

   

  播放段落
  1. What is the cannon ball in this video?
     ::这段视频里的大炮球是什么?
  播放段落
  2. What is used as the monkey in this video?
     ::这段视频里什么是猴子?
  播放段落
  3. Does the velocity of the cannon ball matter, or will it hit the monkey at any velocity?
     ::大炮球的速度重要吗? 还是它会以任何速度击中猴子?